«газпром» временно останавливает обе нитки газопровода «северный поток»
Российский газопровод “Северный поток”, по которому идет газ в Германию, будет остановлен на 10 дней для проведения профилактических работ. Как заявили в компании Nord Stream AG, являющейся оператором газопровода, остановка плановая.
Россия останавливает обе нитки “Северного потока”, поэтому с 11 по 21 июля 2022 года Германия газ получать не будет. В Nord Stream AG пояснили, что остановка плановая, все было согласовано заранее. Между тем цены на газ в Европе уже превысили 1600 долларов за 1 тысячу кубометров на фоне опасений, что Россия сократит поставки газа и европейцы не сумеют заполнить свои ПХГ к зиме. А тут еще и остановка “Северного потока”.
График и план работ были заблаговременно согласованы с партнерами Nord Stream AG по транспортировке газа выше и ниже по потоку
– говорится в сообщении компании-оператора.
Как ранее сообщалось, в середине июня “Газпром” дважды снижал объемы прокачиваемого по “Северному потоку” газа в связи с задержкой ремонта газовых турбин компанией Siemens, который проводился в Канаде. Сначала объем снизился с 167 млн. кубометров газа в сутки до 100, а через день вообще до 67 млн. кубов газа. Как оказалось, был остановлен второй газоперекачивающий двигатель, так как он выработал свой межремонтный ресурс.
Напуганные перспективой остаться без газа немцы попытались договориться с канадцами о возвращении турбины, но у них ничего не получилось. Позднее в Берлине заявили, что решение снизить объемы прокачки приняты по политическим причинам и не связаны с техническими проблемами. А в “Газпроме” намекнули, что имеется еще один газопровод, полностью исправный и готовый к эксплуатации. Немцы сделали вид, что не поняли, о чем идет речь.
Аварии трубопроводов
Безаварийная работа магистральных трубопроводов – одно из основных требований, предъявляемых в газовой и нефтяной отраслях к трубопроводам в связи с их большой протяженностью и старением (значительная часть магистральных трубопроводов в нашей стране находятся в эксплуатации 20-30 лет и более). Выход из строя магистрального трубопровода из-за аварийного отказа может привести к нарушению нормальной работы отдельных экономических районов в связи с перебоями подачи газа, нанести большой материальный ущерб, а часто – и человеческие жертвы. В настоящее время на территории Российской Федерации эксплуатируется 241,6 тысяч километров магистральных и около 350 тысяч километров промысловых трубопроводов. По протяженности подземных трубопроводов для транспортировки нефти и газа Россия занимает второе место в мире после США. При этом основные фонды трубопроводного транспорта России стареют с возрастающей скоростью – например, средний возраст газопроводов Северо-Запада составляет 30 – 35 лет, что неизбежно приближает кризисные явления. Средняя частота аварий в России за последние 10 лет составляет 0,17 аварий/год/1000 км для газопроводов и 0,25 аварий/год/1000 км для нефтепроводов [1, 2]. Основными причинами аварий на трубопроводах являются повреждения в результате внешних воздействий при производстве труб, их монтаже и эксплуатации, а также наружная коррозия, в том числе общая язвенная коррозия и коррозионное растрескивание под напряжением. Наиболее уязвимыми на сегодня являются магистральные газопроводы Северного коридора – многониточной системы газопроводов, проложенных из районов северных месторождений (Уренгойское, Заполярное, Медвежье и др.) до границ Белоруссии с одной стороны и до границы с Финляндией – с другой. В том же коридоре проходит трасса строящегося магистрального газопровода Ямал – Европа. В последние годы выделяется высокая доля аварий именно этого участка магистральных трубопроводов по причине стресс-коррозии (71,0%). В 2003 г. 66,7% аварий также имели стресс – коррозионные характер. Распределение числа аварий по годам здесь представлено на рис.2.1.
Рис.2.1 Распределение аварийных разрушений МГ ООО “Севергазпром” в 1981-2003 гг. для труб диаметром 1020…1420 мм В последние годы в России основной проблемой аварии магистральных газопроводов является стресс-коррозия. Стресс-коррозия является причиной более 50% всех аварий на северо-западных магистралях начиная с 2003 года. Мониторинг состояния почти 10000 км магистральных газопроводов Северного коридора с помощью внутритрубных снарядов-дефектоскопов, выполненный в 2002 году, позволил установить, что из 22.500 дефектов почти половину составляет коррозионные дефекты и дефекты стресс-коррозионного происхождения глубиной от 15 до 30% от толщины стенки трубы. Достаточно большой процент в общем количестве дефектов занимают дефекты проката, ликвационные полосы, зоны расслоений, дефекты кольцевых швов, дефекты продольных сварных швов. Количество дефектов коррозионного растрескивания под напряжением составляет 5-6 на каждом 5-ти километровом участке трубопровода. Таблица 2.1 Данные о разрушениях магистральных газопроводов Северного коридора в процессе эксплуатации за период с 2001 по 2003 годы.
| ||||||||||||
Таким образом, доминирующим механизмом разрушения является коррозионное растрескивание под напряжением (стресс-коррозия).
Растрескивание под напряжением труб происходит при одновременном воздействии растягивающих напряжений, агрессивной среды и при наличии электрохимической антикоррозионной защиты, которая применяется для предотвращения активной почвенной коррозии и электрокоррозии труб. Начальная стадия стресс-коррозионного повреждения представляет собой зарождение продольных поверхностных полуэллиптических трещин, располагающихся в полосе трубы, имеющей обычно размеры не более 400 мм поперек трубы и до нескольких метров в длину. Размеры этой поврежденной области определяются, в основном, состоянием изоляции трубы и размерами области насыщенного водой грунта, в которой создались благоприятные условия для зарождения и развития стресс – коррозионных трещин. Типичный вид стресс-коррозионных трещин показан на рис.2.2.
Рис.2.2 Стресс-коррозионные трещины в трубе аварийного магистрального газопровода.
В процессе развития сети полуэллиптических трещин увеличивается их длина и глубина, пока они не объединяются в единую поверхностную трещину глубиной до 0.5 толщины стенки трубы и длиной, определяющейся протяженностью поврежденной области. Если размеры трещины превысят критические, определяемые характеристиками трещиностойкости материала и напряжениями в трубе, данная трещина явится очагом развития магистральной хрупкой или вязкой трещины. Развитие вязкой магистральной трещины в газопроводах приведет к протяженным разрушениям с тяжелыми последствиями из-за большой энергии сжатого газа в протяженном газопроводе (расстояние между компрессорными станциями составляют многие десятки километров). Вязкие магистральные трещины в нефтепроводах не развиваются из-за отсутствия запасенной энергии в сжатой жидкости (нефти). Типичная поверхностная стресс-коррозионная трещина большой протяженности, образовавшаяся путем слияния отдельных развившихся полуэллиптических стресс-коррозионных трещин, показана на рис.2.3.
Рис.2.3 Поверхностная стресс-коррозионная трещина, послужившая очагом протяженного вязкого разрушения газопровода.
Стресс-коррозия трубопроводов является результатом тяжелых условий эксплуатации подземных трубопроводов, подверженных воздействию почвенных вод различного химического состава, неэффективной полимерной пленочной гидроизоляции большинства эксплуатирующихся в нашей стране трубопроводов и следствием применения электрохимической защиты трубопроводов. Современная многослойная гидроизоляция, выполняемая на заводах-изготовителях труб, является несопоставимо более надежной по сравнению с изоляцией полимерной пленкой, выполнявшейся при прокладке трубопроводов в 60-90 годы прошлого века. Применение современной заводской изоляции позволит в будущем если не решить полностью, то значительно снять остроту проблемы стресс-коррозионных повреждений трубопроводов.
Необходимость электрохимической защиты можно проиллюстрировать случаем протяженного разрушения магистрального газопровода, вызванного локальной электрокоррозией блуждающими токами.
На рис.2.4 и 2.5 приведены соответственно общий вид электро-коррозионного повреждения и профиль трубы в зоне повреждения.
Рис.2.4 Электро-коррозионное повреждение со свищем, развитие которого привело к протяженному разрушению магистрального газопровода. Размер повреждения 200 мм вдоль трубы х 100 мм поперек трубы. Изоляция пленочная. Электрохимическая защита.
Рис.2.5 Профилограмма участка электро-коррозионного повреждения. Номинальный наружный диаметр трубы 1020 мм, толщина стенки 8 мм.
Пример данной аварии говорит об опасности электрокоррозионных повреждений магистральных газопроводов, особенно расположенных рядом с электрифицированными железными дорогами и линиями электропередач. Необходимо улучшение качества изоляции трубопроводов. На трубопроводах с пленочной изоляцией применение электрохимической защиты является, безусловно, необходимой мерой защиты от общей и электро-коррозии. материал труба газопровод металл
Механические повреждения трубопроводов при строительстве и эксплуатации также могут приводить к авариям. Наиболее вероятно образование сквозных дефектов ограниченных размеров, которые при достаточно высокой вязкости металла труб не приводят к протяженным разрушениям. В этом случае образуется свищ, который для газопроводов не является опасным, если может быть вовремя обнаружен и отремонтирован. Для нефтепроводов свищи являются большой проблемой, так как утечка нефтепродуктов приводит к загрязнению окружающей среды.
Таким образом, среди всех видов разрушений можно выделить протяженные вязкие разрушения газопроводов, представляющие наибольшую опасность. Остановимся на них более подробно.
Задания для самостоятельной работы
1. На малом предприятии работают десять семейных пар. Чтобы никому не было обидно, на ежегодном собрании акционеров совет директоров, состоящий из восьми человек, выбирается случайным образом. Найти вероятности следующих событий: а) в совете директоров отсутствуют семейные пары; б) в совете директоров есть ровно одна семейная пара; в) в совете директоров есть ровно две семейных пары?
2. Найти вероятность того, что при раздаче колоды в 52 карты четырём игрокам первый из них получит ровно n пар «туз и король одной масти» (n = 0, 1, 2, 3, 4 ).
3. На 200-километровом участке газопровода между компрессорными станциями A и B происходит утечка газа, которая одинаково возможна в любой точке газопровода. Найти вероятности следующих событий: а) утечка расположена не далее 20 км от A или B; б) утечка расположена ближе к A, чем к B.
4. Чтобы добраться в институт, Петя может воспользоваться автобусом одного из двух маршрутов. Автобусы первого маршрута следуют с интервалом в 18 мин, второго маршрута — с интервалом в в 15 мин. Найти вероятность того, что Петя будет ждать автобуса не более 10 мин.
5. 60. В партии 100 изделий, из которых шесть имеют дефекты. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Найти вероятности следующих событий: а) все бракованные изделия достанутся одному потребителю; б) бракованные изделия достанутся обоим потребителям поровну.
Дополнительные задачи
1. Петя — староста группы. Когда деканат попросил его подать сведения о студентах своей группы, Петя по памяти составил следующую записку: «В группе 45 студентов, в том числе 25 юношей; 30 студентов учатся на “хорошо” и “отлично”, в том числе 16 юношей; 28 студентов занимаются спортом, в их числе 18 юношей и 17 студентов, успевающих на “хорошо” и “отлично”; 15 юношей учатся на “хорошо” и “отлично” и занимаются спортом». Сотрудники деканата сразу определили, что Петя ошибся, и попросили его более аккуратно подойти к выполнению поручения. Как сотрудникам деканата удалось «поймать» Петю?
2. К автобусной остановке через каждые четыре минуты подходит автобус линии А, а через каждые шесть минут — автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего автобуса линии В равновозможен в пределах от нуля до четырех минут.
Определить вероятность того, что:
а) первый подошедший автобус окажется линии А;
б) автобус какой–либо линии подойдет в течение двух минут.
3.4. Рекомендуемая литература
1. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. -К: Вища шк. Головное изд–во. -1988. -439с.
Дата добавления: 2022-10-24; просмотров: 405 | Нарушение авторских прав
mybiblioteka.su – 2022-2022 год. (0.008 сек.)
Задачи на непрерывные распределения
5.26. Во время грозы на участке между 30-м и 70-м километрами телефонной линии произошёл обрыв провода. Считая, что обрыв одинаково возможен в любой точке, найти вероятность того, что обрыв расположен между 40-м и 45-м километрами.
5.27. На 400-километровом участке газопровода между компрессорными станциями A и B происходит утечка газа, которая одинаково возможна в любой точке газопровода. Найти вероятность, того, что утечка расположена не далее 20 км от A или B.
5.28. На отрезке [–4, 8] наудачу взято число. Какова вероятность того, что: а) это число попадет в диапазон от 5 до 6; б) число будет меньше нуля.
5.29. Вероятность попадания случайной величины, распределенной по равномерному закону на (-5, 15) в часть интервала (8; b) равна 1/10. Найти правую границу интервала b.
5.30. Обвал одинаково возможен в любой точке на горной дороге от 30 км до 90 км. Вероятность того, что обвал произойдет в интервале от конца или начала дороги равен 1/5. Найти эти интервалы.
5.31 Все значения равномерно распределённой случайной величины расположены на отрезке [12; 28]. Найти вероятности её попадания: а) на отрезок [24; 28]; б) в интервал (13; 15).
5.32. Ёмкость цистерны для хранения бензина на автозаправочной станции равна 50 т. Найти вероятности событий, состоящих в том, что при случайной проверке в цистерне будет обнаружено: а) менее 5 т бензина; б) более 20 т бензина; в) хотя бы 1 т бензина.
5.33. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.
5.34. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону в интервале от 0 до 60 секунд. Найти плотность распределения и функцию распределения этой случайной величины. Определить вероятность того, что время ожидания ответа не превысит 45 секунд.
5.35. Место дежурства передвижного поста №2 ДПС – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 997 км до 1447 км. Найти плотность распределения и функцию распределения этой случайной величины. Определить вероятность того, что нарушение зафиксируют на интервале от 1200 км до 1300 км.
5.36. Написать плотность и функцию распределения показательного закона, если параметр l = 3.
5.37. Найти параметр l показательного распределения: а) заданного плотностью
,
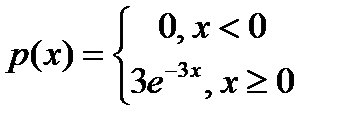б) заданного функцией распределения
.
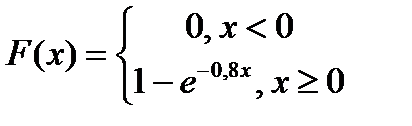5.38. Непрерывная случайная величина X распределена по показательному закону с l=2. Найти вероятность того, что в результате испытания X попадает в интервал (0,1; 0,5).
5.39. Непрерывная случайная величина X распределена по показательному закону, заданному плотностью распределения
.
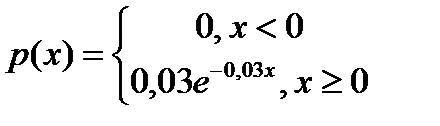Найти вероятность того, что в результате испытания X попадает в интервал (2, 3).
5.40. Как правило, педсовет длится один час. На этот раз за час он не закончился. Какова вероятность того, что он закончится в ближайшие 15 мин, если предположить, что длительность педсовета распределена по показательному закону с l=1.
5.41. Установлено, что время ремонта микроволновой печи является случайной величиной, распределенной по показательному закону. Определить вероятность того, что на ремонт поступившей в мастерскую печи потребуется менее 20 дней, если l = 1/20.
5.42. Время, необходимое для оформления кредита в банке, является случайной величиной, распределённой по показательному закону с параметром l = 0,5 договора/час. Найти вероятность того, что оформление кредита займёт менее 6 ч.
5.43. Время ожидания в очереди имеет показательный закон распределения с параметром l = 3. Какова вероятность того, что покупатель потратит на покупку не менее 10 и не более 15 мин?
5.44. Длительность исполнения заказа в ателье по пошиву брюк имеет показательный закон распределения с параметром l = 1/5. Какова вероятность того, что сданный Вами в ателье заказ выполнят не ранее чем через 4 суток.
5.45. Известно, что 97% смартфонов выходит из строя после 10 000 часов работы. Какова вероятность, что смартфон выйдет из строя в интервале времени от 8000 до 9000 часов, полагая, что время безотказной работы имеет показательный закон распределения с l = 3.
5.46. Написать плотность вероятности нормально распределенной случайной величины X с параметрами s = 3 и а = 2.
5.47. Показания высотомера является нормально распределенной случайной величиной, с параметрами s = 15 м и а = 0 м. Какова вероятность того, что самолет уклонится от расчетной высоты не более чем на 19,5 м?
5.48. Значения теста IQ (коэффициента интеллекта) Стэнфорда – Бине распределены приблизительно по нормальному закону с a = 100 и σ = 16. Найти долю людей, у которых коэффициент интеллекта окажется: а) меньше 60; б) меньше 75; в) меньше 95; г) больше 100; д) больше 120; е) в пределах от 80 до 120.
5.49. При сортировке случайные значения веса зерна распределены нормально с параметрами a = 2 г и σ = 0,4 г. Нормальные всходы дают зерна, вес которых более 1,80 г. Определить процент семян, которые дадут нормальные всходы.
5.50. Случайные отклонения диаметра детали от номинала, выпускаемой цехом, распределены нормально с параметрами a = 20 мм и σ = 0,06 мм. Определить вероятность того, что диаметр наудачу взятой детали имеет размеры от 19 до 22 мм.
5.51. Известно, что вес клубня подчиняется нормальному закону с параметрами a = 125 г и σ = 15 г. Определить вероятность того, что вес наудачу взятого клубня будет: а) не менее 200 г., б) не более 130 г, в) от 98 до 146 г. [а) 0; б) 0,63; в) 0,8833].
5.52. Случайная величина X ~ N(a = 2; σ = 3) . Найти вероятности: а) P{X > 1}, б) P{−2 < X < 2}, в) P{X < 2}. Записать «правило трёх сигм» для этой случайной величины.
5.53. Предполагается, что рост призывников в Южный военный округ будет иметь нормальное распределение с параметрами а = 173 и σ = 6 см. Найти долю летнего обмундирования 3-го (170–176) и 4- роста (176–182), которую следует приготовить к началу осеннего призыва.
5.54. Вес поступивших в продажу плодов манго соответствует нормальному закону распределения с параметром а, равным 0,54 кг. Посчитали, что 5% имеют массу, меньшую 0,5 кг. Каков процент плодов, масса которых: а) менее 0,47 кг; от 0,5 до 0,55 кг, более 0,55 кг?
5.55. Длина карасей, обитающих в водоеме, имеет нормальное распределение с параметром а, равным 25 см. Вероятность того, что длина карася будет от 10 до 15 см равна 0,09. Найти вероятность того, что длина пойманного карася попадет в интервал: а) (35; 40); б) (30, 35).
§
6.1. Задан закон распределения дискретной случайной величины X:
| mi | 0 | 1 | 2 | 3 |
| р i | 0,064 | 0,288 | 0,432 | 0,216 |
Найти: а) математическое ожидание МХ; б) дисперсию DХ; в) среднеквадратическое отклонение σх.
6.2. Случайная величина Х задана законом распределения:
| mi | 10 | 15 | 25 |
| р i | 10/28 | p | 3/28 |
Найти: а) значение вероятности для второй случайной величины; б) математическое ожидание МХ; в) дисперсию DХ.
6.3. Задан закон распределения дискретной случайной величины Х:
| mi | 20 | 21 | 22 | 23 |
| р i | 0,1 | 0,3 | 0,2 | p |
Найти: а) значение вероятности для четвертой случайной величины; б) математическое ожидание МХ; в) дисперсию DХ. [а) 0,4 б) 21,90 в) 1,90]
6.4. Задан закон распределения дискретных случайных величин Х и Y:
| mi | 110 | 120 | 130 | 140 | 150 |
| р ix | 0,15 | 0,20 | 0,35 | 0,1 | 0,2 |
| р iy | 0,1 | 0,15 | 0,3 | 0,05 | 0,4 |
Сравнить а) математические ожидания МХ и М Y и б) стандартные отклонения sx и sy.
6.5. Случайная величина Х задана законом распределения:
Найти третье значение случайной величины и его вероятность, если известно, что ее математическое ожидание равно 4.
6.6. Распределение дискретной случайной величины X содержит неизвестные значения х1 и х2 (х1 < x2):
Известны числовые характеристики случайной величины: MX = 3,6; DX = 0,24. Требуется определить значения х1 и х2.
6.7. Случайная величина X с вероятностью 1/5 принимает значения 7; 9; 10; 11 и 13; а случайная величина Y также с вероятностью 1/5 принимает значения 22; 24; 25; 26; 28. Найти DX и DY , проверить, выполняется ли равенство DY = DX.
6.8. Производится последовательность независимых испытаний 5 приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий – надежный. Построить ряд распределения случайного числа испытаний, если вероятность каждого из них равна 0,9. Найти математическое ожидание, дисперсию.
6.9. На некотором участке дороги 60% водителей соблюдают предусмотренный скоростной режим. Составить закон распределения числа водителей соблюдающих установленные ограничения по скорости, из пяти проехавших. Найти математическое ожидание и дисперсию этой случайной величины.
6.10. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 10 очков. Построить закон распределения числа выбитых очков. Найти математическое ожидание и дисперсию этой случайной величины.
6.11. В некотором цехе брак составляет 10 % всех изделий. Составить закон распределения числа бракованных изделий из трех наудачу взятых, найти математическое ожидание, дисперсию и стандартное отклонение этой случайной величины.
6.12. Производится забрасывание мяча в корзину. Вероятность попадания при одном броске – 0,3. Найти закон распределения, математическое ожидание и дисперсию и стандартное отклонение случайного числа заброшенных мячей при трех бросках.
6.13. В приемное время врача-стоматолога посещает в среднем 6 человек в час. Составить таблицу вероятностей для числа пациентов 0, 1, 2, 3, посетивших психиатра в течение часа в предположении, что количество посетивших стоматолога больных имеет пуассоновское распределение и найти их математическое ожидание.
6.14. В среднем левши составляют 1% всего населения. Сколько в среднем нужно опросить людей, чтобы набрать десятерых левшей в предположении, что количество левшей имеет пуассоновское распределение?
6.15. Из-за сбоя в оборудовании оказалось, что в партии 2% автомобилей имеют скрытый дефект. Определить, сколько автомобилей должен в среднем осмотреть представитель службы качества, чтобы найти один автомобиль с дефектом, если количество дефектных автомобилей в партии имеет пуассоновское распределение.
6.16. Маркетинговые исследования аналитиков компании показали, что 40% горожан предпочитают приобретать продукты в магазинах розничной сети «Магнит». Случайно выбраны 4 человека. Составьте ряд распределения случайной величины Х − числа людей в выборке, предпочитающих услуги данной сети магазинов. Найдите математическое ожидание, дисперсию и стандартное отклонение Х. Чему равна вероятность того, что среди 4 случайно отобранных человек не будет ни одного человека предпочитающего «Магнит»; окажется хотя бы 1 человек предпочитающий «Магнит», будет не больше 3 человек, предпочитающих «Магнит»?
6.17. Среднее число клиентов, приходящих утром в банк в 10-минутный интервал, равно 1. Прибытие клиентов происходит случайно и независимо друг от друга, а их количество подчиняется распределению Пуассона. Составьте ряд распределения для числа клиентов от 1 до 8, прибывающих утром в течение 10 мин. Найдите математическое ожидание, дисперсию случайной величины и стандартное отклонение.
6.18. Из 20 лотерейных билетов выигрышными являются 4. Наудачу извлекаются 4 билета. Составьте ряд распределения числа выигрышных билетов среди отобранных, найдите их математическое ожидание и дисперсию. Определите вероятность того, что среди отобранных 4 билетов окажется: не меньше трех выигрышных билетов, не больше одного выигрышного билета.
6.19. Сделано 2 вклада – 10000 руб. в компанию А и 15000 руб. в компанию В. Компания А обещает 50% годовых, но может «лопнуть» с вероятностью 0,2. Компания В обещает 40% годовых, но может «лопнуть» с вероятностью 0,15. Составить закон распределения случайной величины Х – общей суммы прибыли (убытка), полученной от 2-х компаний через год.
6.20. Нефтяная компания получила финансирование для проведения 10 разработок залежей нефти. Вероятность успешной разработки 0,01. Нефтяные разработки осуществляются независимо друг от друга. Найти математическое ожидание и дисперсию числа успешных разработок.
6.21. Распределение дискретной случайной величины Х задано формулой Р(Х = k) = c/2к, k = 0,1,2,… Найти c, Р(Х ≤ 3).
6.22. Вероятность того, что студент сдаст семестровые экзамены по алгебре, математическому анализу, физике равны соответственно 0,6; 0,7; 0,9. Составить закон распределения Х – числа семестровых экзаменов, которые сдаст студент.
6.23. Студент купил 4 билета новогодней лотереи. Вероятность выигрыша по одному билету равна 0,6. Составить закон распределения числа выигрышей, найти математическое ожидание и дисперсию.
6.24. Непрерывная случайная величина Х задана дифференциальной функцией распределения р(x):
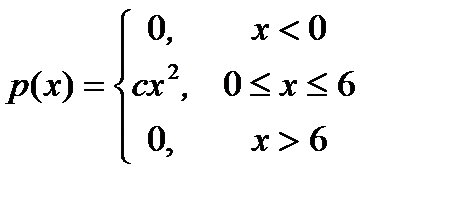
Найти: а) значение параметра с; б) интегральную функцию распределения F ( x ); в) математическое ожидание и дисперсию случайной величины.
6.25. Непрерывная случайная величина Х задана дифференциальной функцией распределения р(x):
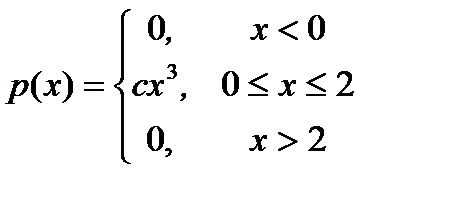
Найти: а) значение параметра с; б) интегральную функцию распределения F ( x ); в) математическое ожидание и дисперсию случайной величины.
6.26. Непрерывная случайная величина Х задана интегральной функцией распределения F ( x ):
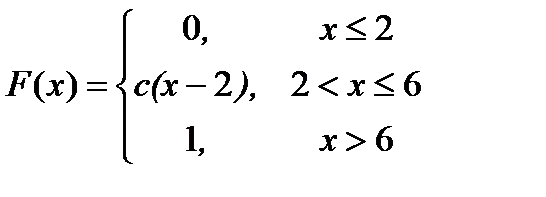
Найти: а) значение параметра с; б) дифференциальную функцию распределения р( x ); в) математическое ожидание и дисперсию случайной величины; г) вероятность того, что случайная величина Х попадет в интервал
(-1; 3).
6.27. Непрерывная случайная величина Х задана интегральной функцией распределения F ( x ):
.
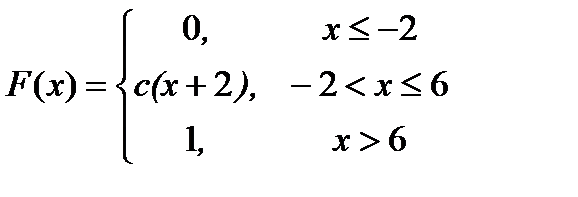Найти: а) значение параметра с; б) дифференциальную функцию распределения р(x); в) математическое ожидание и дисперсию случайной величины; г) вероятность того, что случайная величина Х попадет в интервал (0; 2).
а)1/8; б)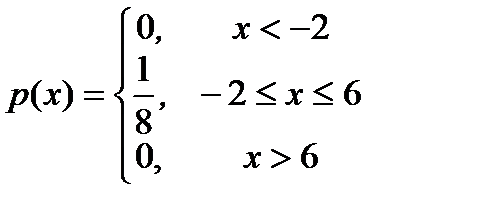 
в) 2; 16/3; 
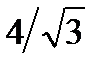г) 1/4
6.28. Непрерывная случайная величина Х задана интегральной функцией распределения F ( x ):
.
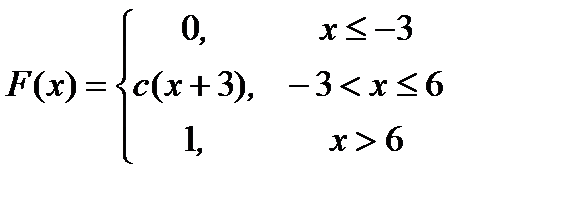Найти: а) значение параметра с; б) дифференциальную функцию распределения р( x ); в) математическое ожидание и дисперсию случайной величины; г) вероятность того, что случайная величина Х попадет в интервал (0; 5).
6.29. Непрерывная случайная величина Х задана интегральной функцией распределения F ( x ):
.
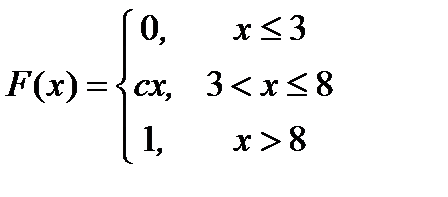Найти: а) значение параметра с; б) дифференциальную функцию распределения р(x); в) математическое ожидание и дисперсию случайной величины; г) вероятность того, что случайная величина Х попадет в интервал (0; 5).
6.30. Время, необходимое для оформления договора, является случайной величиной, распределённой по показательному закону со средним значением 10/3. Найти вероятность того, что оформление договора займёт менее 7 ч.
6.31. Среднее время ожидания трамвая равно 3,5 мин. Известно, что время ожидания имеет равномерный закон распределения. Минимальное время ожидания равно 0. Найти вероятность того, что пассажир будет ожидать трамвай от двух до пяти минут.
6.32. Случайная величина X распределена по экспоненциальному закону и имеет среднее значение, равное 1/2. Определить вероятности P{X > 1}, P{X < 2}, P{X > −1}, P{X = 3} и дисперсию этой случайной величины.
6.33. Случайная величина X равномерно распределена на отрезке [0;100]. Найти вероятности P{X > 10}, P{40 < X < 90} а также математическое ожидание и дисперсию этой случайной величины.
6.34. Случайная величина Х, сосредоточенная на интервале (1,4) задана квадратичной функцией распределения F(x) = a·x2 b·x c, имеющей максимум при x = 4. Найти параметры а, в, с и вычислить вероятность попадания Х в (2, 3).
6.35. Плотность распределения случайной величины Х имеет вид:
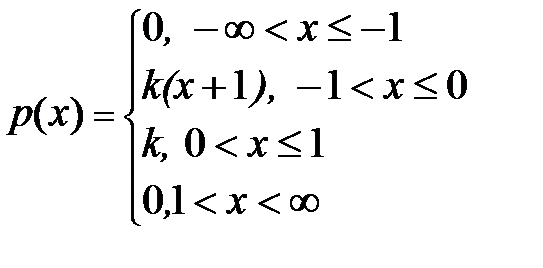
Найти k, МХ, Р(-0,5< Х<0,5), F(х).
