Основные понятия, связанные с изучением турбулентного потока
1°. Мгновенная местная скорость (актуальная скорость). Структуру турбулентного потока можно себе представить, например, в следующем виде.
При больших скоростях некоторые объемы жидкости (а, b, с; рис. 4-8) разной величины и формы приходят внутри жидкости в беспорядочное не установившееся вращение (получаются водовороты). Множество этих водоворотов, возникающих внутри жидкости и распадающихся на более мелкие изменяется по течению. Имея поступательное движение, они проносятся через данное поперечное сечение потока I – I. Если на этом сечении потока зафиксировать неподвижную точку А, принадлежащую пространству, то через эту точку будут проходить частицы жидкости, имеющие поступательное и вращательное 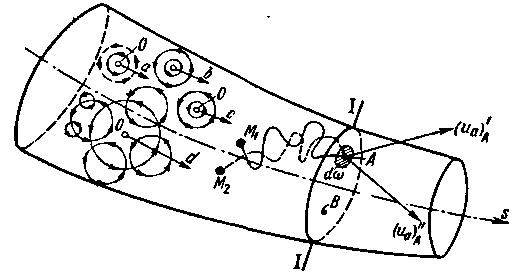
Рис. 4-8. Схема турбулентного движения
движения (относительно перемещающихся центров О); скорость в точке А поэтому все время должна изменяться (и по величине и по направлению)[8]
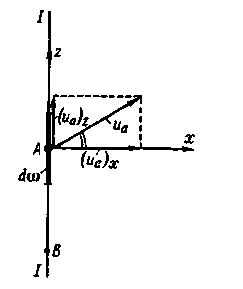
Рис. 4-9. Продольная актуальная скорость [(ua)x] и поперечная актуальная скорость [(ua)z]
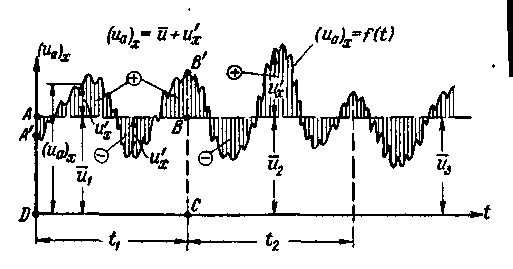
Рис. 4-10. Схема графика пульсаций продольной актуальной скорости для неподвижной точки пространства А (рис. 4-8) u – осредненная продольная скорость
В результате, если в толще потока наметить несколько частиц жидкости (М1 М2, …), попадающих в точку А в разные моменты времени t, то получим следующую картину:
а) частица М1, двигаясь по некоторой причудливой траектории, попадает в точку А в момент времени t1 и приобретает в этой точке скорость, которую обозначим через (uа)’А;
б) частица М2, двигаясь по другой траектории, попадает в точку А в момент времени t2 и приобретает в этой точке скорость (uа)”А, отличную от скорости (uа)’А, и т. д.
В другой точке поперечного сечения I – I, например, в точке В, будем иметь аналогичную картину; для различных моментов времени (t1 t2, …) будем получать в этой точке различные скорости: (uа)’В; (uа)”В; (uа)”’В и т.д.
Действительную скорость uа движения жидкой частицы в данный момент времени в данной точке пространства (например, в точке А или В) называют мгновенной местной скоростью или актуальной скоростью[9]
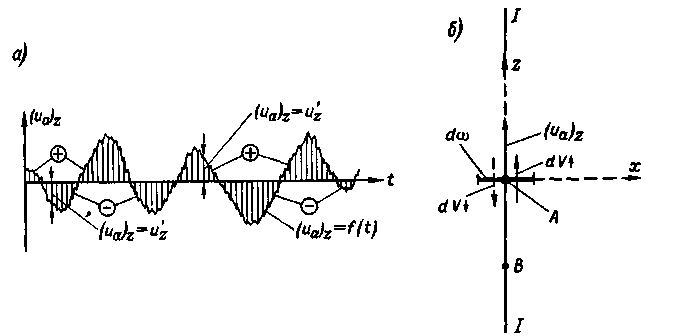
Рис. 4-11. Продольное и поперечное направления турбулентного потока: а — схема графика пульсаций поперечной актуальной скорости для неподвижной точки А пространства; б — поперечный обмен объемами жидкости dV (через площадку dω)
Как видно, актуальная скорость в данной точке пространства изменяется во времени (в общем случае и по величине и по направлению).
2°. Пульсация мгновенной местной (актуальной) скорости.Представим на I рис. 4-9 схему плоского поперечного сечения I – I потока и отметим на нем точку А и элементарную площадку dω, выделенную у этой точки. Проведем к площадке dω нормаль Ах и ортогональ к этой нормали Az; изобразим вектор скорости иа. Далее спроектируем иaна направления Ах и Az, причем получим составляющие (иа)хи (ua)z.[10]
Продольная составляющая актуальной скорости (иа)хбудет характеризоваться следующим:
а) она всегда будет иметь постоянное направление (в отличие от скорости иа);
б) величина ее будет изменяться во времени (соответственно тому, как
изменяется во времени величина скорости иа).
Составляющие (иа)хи (иа)zбудем именовать соответственно: мгновенной продольной составляющей скорости (или просто продольной скоростью) и мгновенной поперечной составляющей скорости (или просто поперечной скоростью).
Изменение (иа)хво времени в данной точке пространства может быть представлено графиком на рис. 4-10. Этот график, относящийся к определенной точке пространства (например, к точке А), называется графиком пульсации продольной скорости.
Аналогично можно построить график пульсации поперечной скорости (ua)z(рис. 4-11,а).
Пульсацией скорости называется явление изменения (увеличение и уменьшение) во времени (т. е. явление флюктуации) величины проекции местной мгновенной (актуальной) скорости на какое-либо направление (например, на линию Ах или на линию Az). С явлением пульсации скоростей иногда сталкиваемся в обыденной жизни; например, наблюдая водоросли, растущие в текущей воде реки, можно заметить, что эти водоросли совершают сложные колебательные движения, которые являются результатом пульсации скоростей; наблюдая уровень воды в трубке Пито, можно видеть, что этот уровень колеблется: то поднимается, то опускается, что также объясняется пульсацией скорости.
3°. Осредненная местная скорость. Пульсационная скорость (пульсационная добавка).Выделим на графике пульсации продольной составляющей скорости (рис. 4-10), относящемся к определенной точке пространства А, достаточно большой отрезок времени t1 и затем в пределах этого отрезка осредним величины (иа)х: проведем прямую АВ с таким расчетом, чтобы площадь прямоугольника ABCD (ΩABCD)равнялась площади фигуры A’B’CD (ΩA‘B‘CD) ограниченной кривой графика пульсации:
ΩABCD = ΩA‘B‘CD
При этом получим некоторое среднее значение u1, продольной скорости в данной точке А (как здесь, так и ниже, индексы х у осредненных продольных составляющих опускаем).
Выделим далее второй достаточно большой отрезок времени t2; проведя осреднения продольных мгновенных скоростей в пределах этого отрезка времени, получим некоторое среднее значение 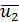 продольной скорости в той же, точке А и т. д.
продольной скорости в той же, точке А и т. д.
Турбулентное движение жидкости является движением неустановившимся, так как здесь в данной точке пространства актуальные скорости ua все время изменяются. Вместе с тем, если для данной точки А живого сечения (а также и для других точек этого живого сечения) величины 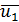 ,
, 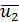 ,
,  , …, найденные, как это описано выше, удовлетворяют условиях (рис. 4-10)
, …, найденные, как это описано выше, удовлетворяют условиях (рис. 4-10)
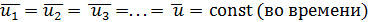 (4-47)
(4-47)
то такое турбулентное движение может быть названо в среднем установившимся движением; такого рода движение часто называют просто установившимся, опуская слово «в среднем» (но подразумевая его). Как ясно из сказанного, на рис. 4-10 представлен случай установившегося турбулентного движения. Для неустановившегося турбулентного движения будем иметь 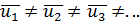 Условная (фиктивная) скорость
Условная (фиктивная) скорость 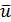 называется осредненной местной скоростью; эта скорость является, разумеется, продольной.
называется осредненной местной скоростью; эта скорость является, разумеется, продольной.
Если через dV обозначить объем жидкости, проходящей через элементарную площадку dω (рис. 4-9) за достаточно большой отрезок времени t, то величину осредненной местной скорости при установившемся (в среднем) движении можно представить соотношением
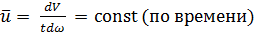 (4-48)
(4-48)
Рассматривая рис. 4-10, видим, что продольная актуальная скорость ( 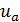 )х может быть представлена в виде:
)х может быть представлена в виде:
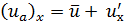 , (4-49)
, (4-49)
где величина 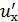 (положительная или отрицательная) может быть названа продольной пульсационной скоростью или пульсационной добавкой.
(положительная или отрицательная) может быть названа продольной пульсационной скоростью или пульсационной добавкой.
Легко видеть, что для достаточно большого промежутка времени t
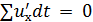 (4-50)
(4-50)
поскольку левая часть этого равенства выражается суммой площадей (положительных и отрицательных), показанных на рис. 4-10 штриховкой.
Рассматривая пульсацию поперечных (по отношению к общему направлению течения) составляющих актуальной скорости, т. е. пульсацию величин (uа)z (рис. 4-11), должны иметь в виду элементарную площадку dω, ортогональную оси Oz (рис. 4-11,б). Через эту площадку в связи с наличием скоростей (uа)z (изменяющихся во времени как по величине, так и по направлению) будет двигаться жидкость. Обозначим: через dV↑ — объем этой жидкости, прошедшей через площадку dω вверх в продолжении длительного промежутка времени t; через dV↓ — объем жидкости, прошедшей через площадку dω вниз в течение того же отрезка времени t.
Для установившегося (в среднем) турбулентного движения (при достаточно большом t) будем иметь равенство (см. конец настоящего пункта):
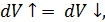 (4-51′)
(4-51′)
отсюда можем заключить, что объем жидкости dV, прошедший через площадку dω за время t, должен быть равен нулю:
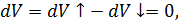 (4-51′′)
(4-51′′)
а следовательно, осредненная поперечная местная скорость
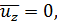 (4-52′)
(4-52′)
Имея это в виду, можем написать [сообразуясь с аналогичной зависимостью (4-49), в которой мы понимаем под 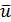 величину
величину 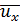 ], что
], что
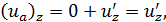 (4-52′′)
(4-52′′)
где и’zможно назвать поперечной пульсационной скоростью. Как видно, поперечная составляющая актуальной скорости является поперечной пульсационной скоростью. Ясно, что для достаточно большого отрезка времени
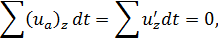
и следовательно, сумма положительных площадей графика пульсации (рис. 4-11, а) равна сумме отрицательных площадей данного графика.
Необходимо в заключение подчеркнуть, что все сказанное выше основан на том предположении, что продольное («главное») и поперечное направления движения жидкости (т. е. направления осей Ах и Az; см. рис. 4-9) были выбраны в начале наших рассуждений с таким расчетом, чтобы соотношение (4-51″) было удовлетворено.
4°. Пульсация давлений. Осредненный поток (модель Рейнольдса — Буссинеска). Как показывает опыт, пульсация скоростей сопровождается пульсацией давлений р, т.е. изменением во времени величин р в точках пространства. Рассматривая в среднем установившееся турбулентное движение, можем считать, что для заданной точки пространства (например, точки А на рис. 4-8)
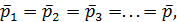 (4-53)
(4-53)
где 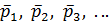 — гидродинамические давления, осредненные в точке А за достаточно большие отрезки времени (следующие один за другим) t1 t2, t3, ..; величина
— гидродинамические давления, осредненные в точке А за достаточно большие отрезки времени (следующие один за другим) t1 t2, t3, ..; величина 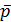 может быть названа осредненным местным гидродинамическим давлением.
может быть названа осредненным местным гидродинамическим давлением.
Для расчета турбулентного потока О. Рейнольде (в 1895 г.) и Ж. Буссинеск (1897 г.) предложили заменять этот поток некоторой воображаемой моделью, представляющей собой условный (фиктивный) поток жидкости, частицы которой движутся со скоростями, равными осредненным местным (продольным) скоростям (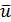 ), гидродинамические же давления в различных точках пространства, занятого этим потоком, равны осредненным местным давлениям
), гидродинамические же давления в различных точках пространства, занятого этим потоком, равны осредненным местным давлениям 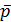 . Такой воображаемый поток будем называть осредненным потоком или мо-делью Рейнольдса — Буссинеска. Как видно, поперечные актуальные скорости (ua)zпри переходе к такой модели исключаются из рассмотрения, т. е. исключается из рассмотрения так называемое «турбулентное перемешивание» (поперечный обмен частицами жидкости между отдельными продольными ее слоями).
. Такой воображаемый поток будем называть осредненным потоком или мо-делью Рейнольдса — Буссинеска. Как видно, поперечные актуальные скорости (ua)zпри переходе к такой модели исключаются из рассмотрения, т. е. исключается из рассмотрения так называемое «турбулентное перемешивание» (поперечный обмен частицами жидкости между отдельными продольными ее слоями).
Если при движении, называемом нами установившимся, величины 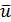 в отдельных точках пространства не изменяются во времени, то при движении, которое мы будем именовать неустановившимся, величины
в отдельных точках пространства не изменяются во времени, то при движении, которое мы будем именовать неустановившимся, величины 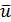 должны при рассмотрении модели Рейнольдса —Буссинеска изменяться во времени.
должны при рассмотрении модели Рейнольдса —Буссинеска изменяться во времени.
Как видно, рассчитывая турбулентный поток согласно Рейнольдсу — Буссинеску, мы должны оперировать величинами 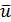 и
и 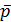 . Поэтому, прилагая, например, уравнение Бернулли к определенному турбулентному потоку, в этом уравнении под величинами и и р всегда следует подразумевать величины
. Поэтому, прилагая, например, уравнение Бернулли к определенному турбулентному потоку, в этом уравнении под величинами и и р всегда следует подразумевать величины 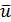 и
и 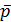 ; только для упрощения записи в этом случае над буквами и и р не ставят горизонтальных черточек, указывающих на осреднение величин и и р во времени, однако эти черточки всегда подразумевают. Что касается интенсивности пульсации скоростей (иа)х, то при указанном подходе к вопросу это обстоятельство может быть учтено в уравнении Бернулли величиной корректива αс(см. ниже п. 6°).
; только для упрощения записи в этом случае над буквами и и р не ставят горизонтальных черточек, указывающих на осреднение величин и и р во времени, однако эти черточки всегда подразумевают. Что касается интенсивности пульсации скоростей (иа)х, то при указанном подходе к вопросу это обстоятельство может быть учтено в уравнении Бернулли величиной корректива αс(см. ниже п. 6°).
Действительные линии тока в случае турбулентного потока должны представлять собой весьма неопределенные кривые, всегда меняющиеся во времени. При рассмотрении же осредненного потока (модели Рейнольдса—Буссинеска) получаем среднестатистические линии (или поверхности) тока (построенные на основе скоростей и) и среднестатистические элементарные струйки, которые не изменяются во времени, если мы имеем установившееся движение (в среднем). Для такого движения указанные среднестатистические поверхности тока должны быть образованы площадками, характеризующимися условием (4-51′).
Надо отметить, что живые сечения осредненного потока, также как и живые сечения действительного ламинарного потока, не являются поверхностями равного напора Не. Осредненный поток дает нам вихревое (не потенциальное) движение.
Следует подчеркнуть, что исключаемое из рассмотрения турбулентное перемешивание (при переходе к осредненному потоку) существенно влияет на величину потерь напора; это обстоятельство приходится дополнительно учитывать так, как то поясняется в § 4-7.
В некоторых случаях практики при турбулентном движении жидкости в нее можно ввести (в весьма малом количестве) особые полимерные добавки, которые, двигаясь вместе с жидкостью, приглушают турбулентное перемешивание, причем, как показывает опыт, потери напора резко снижаются. Подчеркнем, что, как видно из всего сказанного выше, модель Рейнольдса — Буссинеска (модель осредненного потока), которой для расчета мы заменяем действительный турбулентный поток, представляет собой некоторый особый воображаемый ламинарный поток.
5. Средняя скорость при турбулентном движении жидкости.Не следует смешивать термины «средняя скорость» v и «осредненная скорость» u.[11]В первом случае мы проводили осреднение по живому сечению (для данного момента времени), во втором случае — по времени (в данной точке пространства).
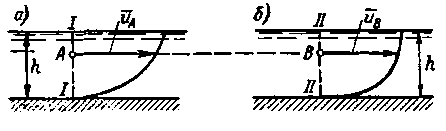
Рис. 4-12. Сопоставление потоков, характеризуемых различной интенсивностью пульсации скоростей
В случае ламинарного движения скорость v есть средняя из действительных скоростей и. В случае же турбулентного движения скорость v есть средняя не из действительных скоростей, а уже из осредненных скоростей; чтобы получить скорость v, в этом случае следует дважды прибегать к осреднению; сперва осредняем продольные скорости по времени в отдельных точках поперечного сечения, а затем полученные и осредняем по поперечному сечению потока.
6°. Кинетическая энергия турбулентного потока.Изобразим на рис. 4-12 два одинаковых призматических русла; будем считать, что потоки на рис. 4-12 характеризуются одинаковыми расходами Q и одинаковыми глубинами h, а следовательно, одинаковыми средними скоростями v.
Рассмотрим два живых сечения: I – I (рис. 4-12,а) и II – II (рис. 4-12,6). Предположим, что в некоторых двух сходственных точках А и В указанных живых сечений осредненные продольные скорости иАи ивоказались равными: uА= ив. При таком положении в намеченных сходственных точках (А и В) пульсация скоростей (иа)хможет быть, вообще говоря, различной; например, в точке А размах пульсации может быть большим (рис. 4-13,а)[12], а в точке В — малым (рис. 4-13,б).
Сопоставляя между собой потоки на рис. 4-12, а и б, легко видеть, что оба эти потока, имея одинаковую среднюю скорость v, в общем случае могут характеризоваться различной структурой. При этом поток с повышенной турбулентностью (рис. 4-13, а) всегда будет обладать большей кинетической энергией.
Можно считать, что кинетическая энергия турбулентного потока слагается из двух величин:
а) кинетической энергии, подсчитанной исходя из осредненных скоростей и;
б) кинетической энергии, подсчитанной исходя из пульсационных скоростей u′.
Если в случае ламинарного режима удельная кинетическая энергия выражается величиной 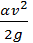 , где α — корректив, учитывающий только неравномерность распределения скоростей по живому сечению (корректив кинетической энергии), то в случае турбулентного режима удельная кинетическая энергия выражается величиной
, где α — корректив, учитывающий только неравномерность распределения скоростей по живому сечению (корректив кинетической энергии), то в случае турбулентного режима удельная кинетическая энергия выражается величиной 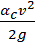 , где
, где
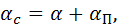 (4-54)
(4-54)
причем здесь αп — дополнительный корректив, учитывающий пульсацию продольных скоростей (иа)хв отдельных точках поперечного сечения потока.
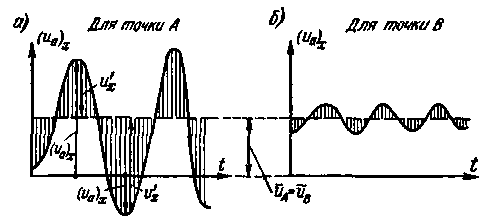
Рис. 4-13. Графики пульсации продольной актуальной скорости для потоков на рис. 4-12
Величину αп приходится, однако, учитывать только при наличии интенсивной турбулентности, которая может иметь место при неравномерном движении; для турбулентного равномерного движения величиной αп можно пренебрегать.
Заметим в заключение, что в связи с различной степенью пульсации скоростей для потоков на рис. 4-12, а и б, распределение осредненных скоростей и по живым сечениям для этих потоков должно получиться разным (формы эпюры скоростей на рис. 4-12,а и б должны быть различными; см. § 4-7 и 4-8).
§
В действительном турбулентном потоке имеются обычные касательные напряжения τ, называемые актуальными. Поле таких напряжений, в связи с турбулентностью, должно изменяться во времени. Если бы для данного момента времени нам было известно такое поле, то мы могли бы для этого момента времени, используя обобщенный закон Ньютона (см. сноску на с. 136), вычислить с некоторым приближением и поле актуальных касательных напряжений.
«Турбулентные касательные напряжения» τт не следует смешивать с актуальными напряжениями т действительного турбулентного потока. Напряжения τт не существуют в действительном потоке; они являются воображаемыми; их мысленно вводят в осредненный поток (в модель Рейнольдса — Буссинеска), чтобы в определенном отношении (см. ниже) приблизить модель осредненного потока к действительности.
Поясним этот вопрос подробнее.
Переходя от действительного турбулентного потока к осредненному потоку (к модели), мы отбрасываем поперечные пульсационные скорости u’z = uz. В модели осредненного потока остаются только продольные составляющие скоростей, т. е. величины их (которые условно обозначают буквой u)
Вместе с тем, отброшенные скорости uz влияют на формирование эпюры продольных скоростей и, а следовательно, влияют и на величину потерь напора.
Имея это в виду, чтобы компенсировать влияние (на эпюру продольных скоростей) отбрасываемых скоростей uz, и было предложено ввести в модель осредненного потока воображаемые (несуществующие) продольные касательные напряжения τт. При этом величину τт. стремятся подобрать так, чтобы количественное влияние τт. на эпюру скоростей и соответствовало количественному влиянию на эту же эпюру отброшенных поперечных скоростей uz,.
Рис. 4-14. К вопросу о турбулентных касательных напряжениях: а — «действительный» поток; имеет место поперечный обмен частицами жидкости (исключенный при переходе к осредненному потоку); б — модель осредненного потока; введены воображаемые касательные напряжения τт (компенсирующие исключенные скорости иz)
На рис. 4-14, а представлена схема действительного потока, который характеризуется наличием поперечного обмена частицами жидкости: см. на рисунке «черные» частицы, которые имеют относительно большие продольные скорости и1причем эти частицы со скоростью uz↓ переходят в нижний (2-й) слой жидкости и ускоряют его движение; см. также на этом рисунке «белые» частицы, которые имеют относительно малые продольные скорости uz, причем они со скоростью иz↑ переходят из 2-го слоя в 1-й слой жидкости и замедляют движение этого слоя. На схеме а показаны две эпюры скоростей: эпюра № 1 —действительная эпюра продольных скоростей и и эпюра № 2 — искаженная эпюра, получающаяся в том случае, если исключим из рассмотрения скорости uz[13].
На рис. 4-14,6 показана схема модели Рейнольдса — Буссинеска, которая характеризуется отсутствием турбулентного обмена (uz = 0); для такой схемы мы должны получить упомянутую выше искаженную эпюру скоростей № 2; однако, вводя в эту схему вместо скоростей uzвоображаемые касательные напряжения τт (соответствующей величины), мы можем исправить искаженную эпюру № 2 и получить вместо нее «истинную» эпюру № 1.[14]Как видно, в действительном потоке (схема а) действуют только «ньютоновские касательные напряжения» τ. (§ 4-3); в модели Рейнольдса — Буссинеска (схема б) вдоль поверхности 1 — 1 действуют касательные напряжения равные (τ τт).
Чтобы определить необходимую величину τт, используют как бы постулат, который условно можно представить такой записью:[15]
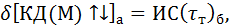
где в левой части уравнения приводится приращение количества движения (КД) некоторого элементарного объема жидкости на соответствующем его перемещении, обусловленное турбулентным обменом; как видно, эта часть уравнения относится к действительному потоку (рис. 4-14,а); в правой части уравнения приводится импульс воображаемых сил трения (на соответствующем перемещении); эта часть уравнения относится к воображаемому потоку (рис. 4-14,6).
Из сказанного, между прочим, вытекает, что приведенная выше зависимость не может быть названа уравнением количества движения (импульса сил), поскольку левая и правая части этого уравнения относятся к различным объектам: левая к действительному потоку, а правая — к воображаемому потоку.
Решая особым (весьма приближенным) способом уравнение, отражаемое приведенной выше условной записью, Буссинеск получил формулу для τт, по своей структуре совпадающую с зависимостью (4-24):[16]
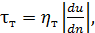 (4-55)
(4-55)
где 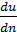 – градиент скорости; он имеет тот же смысл, что и в зависимости (4-24); здесь только под u надо понимать осредненную продольную скорость;[17]
– градиент скорости; он имеет тот же смысл, что и в зависимости (4-24); здесь только под u надо понимать осредненную продольную скорость;[17] 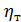 – коэффициент пропорциональности, называемый динамическим коэффициентом турбулентной вязкости или турбулентного обмена.[18]
– коэффициент пропорциональности, называемый динамическим коэффициентом турбулентной вязкости или турбулентного обмена.[18]
Согласно Л. Прандтлю коэффициент 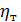 выражается зависимостью (полученной в предположении отсутствия молекулярной вязкости):
выражается зависимостью (полученной в предположении отсутствия молекулярной вязкости):
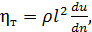 (4-56)
(4-56)
где величину l принято называть длиной пути смешения или перемешивания; разные авторы приписывают величине l различный физический смысл; данную величину выражают в виде
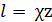 (4-57)
(4-57)
где z — расстояние от стенки русла до точки, в которой определяется турбу-лентное касательное напряжение; χ — «универсальная постоянная Прандтля»; согласно опытам Никурадзе для круглой трубы χ«0,4.
Как видно из (4-56), величина динамического коэффициента 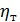 пропор-циональна градиенту скорости, причем коэффициент
пропор-циональна градиенту скорости, причем коэффициент 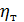 в отличие от коэф-фициента
в отличие от коэф-фициента 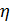 (коэффициента молекулярной вязкости) зависит от характера движения жидкости.
(коэффициента молекулярной вязкости) зависит от характера движения жидкости.
Аналогично (3-128) можем написать [учитывая также зависимость (4-56)]:
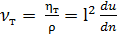 , (4-58)
, (4-58)
где 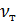 называется кинематическим коэффициентом турбулентной вязкости или турбулентного обмена.
называется кинематическим коэффициентом турбулентной вязкости или турбулентного обмена.
В общем случае осредненный поток должен одновременно обладать и молекулярной и турбулентной вязкостями. Поэтому полное суммарное касательное напряжение τ. записывают иногда (с некоторым приближением) в виде
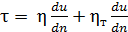 , (4-59)
, (4-59)
В случае ламинарного движения второй член правой части (4-59) отпадает; при этом напряжение трения на стенке 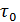 получается пропорциональным первой степени средней скорости. В случае турбулентного движения при достаточно больших числах Рейнольдса второй член правой части (4-59) значительно превышает первый; при этом с молекулярной вязкостью можно вовсе не считаться; в результате τ оказывается прямо пропорциональным второй степени средней скорости (см. ниже § 4-9).
получается пропорциональным первой степени средней скорости. В случае турбулентного движения при достаточно больших числах Рейнольдса второй член правой части (4-59) значительно превышает первый; при этом с молекулярной вязкостью можно вовсе не считаться; в результате τ оказывается прямо пропорциональным второй степени средней скорости (см. ниже § 4-9).
В случае турбулентного движения в условиях не слишком больших чисел Рейнольдса оба слагаемых правой части (4-59) могут получиться соизмеримыми, причем 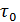 оказывается пропорциональным средней скорости в степени, не равной двум.
оказывается пропорциональным средней скорости в степени, не равной двум.
Для осредненного турбулентного потока, когда действует зависимость (4-59), эпюра турбулентных касательных напряжений 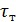 для круглой трубы может быть схематично представлена площадью Оса (см. рис. 4-4); на этом рисунке через
для круглой трубы может быть схематично представлена площадью Оса (см. рис. 4-4); на этом рисунке через  обозначены касательные напряжения, обусловленные молекулярной вязкостью.
обозначены касательные напряжения, обусловленные молекулярной вязкостью.
Необходимо учитывать, что при желании описать то или другое достаточно сложное физическое явление (например, явление турбулентного движения жидкости) приближенной математической зависимостью, устанавливающей связь между различными характеристиками (параметрами) данного явления, часто поступают следующим образом. Сперва создают в своем воображении так называемую неполную модель данного явления (неполную в том смысле, что эта модель не полностью отражает рассматриваемое явление, несколько схематизируя, упрощая его). После этого подвергают анализу с использованием аппарата механики и математики не действительность (которая сложна и поэтому недоступна указанному анализу), а принятую неполную воображаемую модель. Именно, исходя из такой модели, и получают соответствующие расчетные зависимости и формулы. Само собой разумеется, что эти зависимости могут считаться приемлемыми только после экспериментальной их проверки (и часто после введения в них соответствующих поправочных коэффициентов, учитывающих отличие принятой модели от действительности). Различные авторы при исследовании определенного явления могут принимать различные модели и получать при этом разные результаты. Само собой разумеется, что удачной моделью будет та, которая приведет нас к результатам, достаточно хорошо согласующимся с опытными данными. Иногда мы можем столкнуться с таким случаем, когда модель, по своему виду больше отличающаяся от действительности, дает лучшие количественные результаты, чем модель, отличающаяся от действительности в меньшей мере и т. п.
Именно с учетом высказанных соображений и следует рассматривать решения, упоминавшиеся выше, а также решения, о которых мы будем говорить в последующем изложении.
Из вывода, приведенного в § 2-2, можно видеть, что, прилагая к граням рассматриваемой в этом параграфе призмы касательные напряжения, мы при этом должны изменить величину нормальных напряжений с тем, чтобы элементарная призма осталась в равновесии (в данном случае в «динамическом равновесии»). Поэтому можно утверждать, что осредненный поток (модель Рейнольдса — Буссинеска) должен характеризоваться наличием не только дополнительных турбулентных касательных напряжений, но и наличием еще дополнительных турбулентных нормальных напряжений.
В заключение отметим, что рассматривая осредненный поток вязкой (реальной) жидкости и прилагая к нему уравнение Навье — Стокса (см. § 3-3), Рейнольдс получил три особых уравнения равновесия жидкости, учитывающих осреднение потока во времени. Эти уравнения, «содержащие некоторые дополнительные члены, называются уравнениями Рейнольдса (их мы не приводим).
§
ПО ЖИВОМУ СЕЧЕНИЮ ПОТОКА ПРИ ТУРБУЛЕНТНОМ РАВНОМЕРНОМ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ.
ВЯЗКИЙ ПОДСЛОЙ. ГЛАДКИЕ И ШЕРОХОВАТЫЕ ТРУБЫ.
ПОГРАНИЧНЫЙ СЛОЙ
1°. Общий характер распределения осредненных скоростей по живому сечению потока при турбулентном движении. Вязкий подслой.Представим на рис. 4-15 эпюру осредненных скоростей для живого сечения АВ. Как показывает опыт, эта эпюра характеризуется следующим:
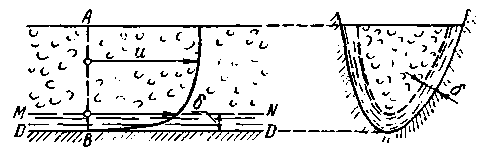
Рис. 4-15. Эпюра скоростей (осредненных) при турбулентном движении; 𝛿 — толщина вязкого подслоя
1) вблизи стенок скорость u вдоль линии ВА резко увеличивается, т. е. в этом месте 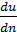 имеет большую величину;
имеет большую величину;
2) на некотором удалении от стенки и изменяется относительно мало; 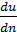 в этом месте имеет относительно малую величину.
в этом месте имеет относительно малую величину.
При помощи подкрашивания движущейся жидкости можно убедиться в том, что жидкость из центральной части потока переносится к боковым границам потока; наоборот, жидкость от границ потока (с низшим содержанием кинетической энергии) переносится к центру потока. Именно в результате такого турбулентного перемешивания распределение скоростей по живому сечению в средней части потока оказывается при турбулентном движении значительно более равномерным, чем при ламинарном.
Если в случае ламинарного напорного движения в круглой трубе 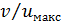 = 0,5 (где
= 0,5 (где 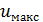 — скорость по оси трубы), то в случае турбулентного движения в такой трубе обычно, как показывает опыт,
— скорость по оси трубы), то в случае турбулентного движения в такой трубе обычно, как показывает опыт, 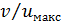 = 0,70 ÷ 0,90 (с увеличением числа Рейнольдса Re это отношение увеличивается; оно зависит также от шероховатости стенок русла).
= 0,70 ÷ 0,90 (с увеличением числа Рейнольдса Re это отношение увеличивается; оно зависит также от шероховатости стенок русла).
Согласно исследованиям Л. Прандтля в турбулентном потоке скорость движения жидких частиц непосредственно у стенки равна нулю. В соответствии с этим принято считать, что вблизи стенок русла имеется тонкий слой жидкости толщиной 𝛿, где скорости столь малы, что в пределах этого слоя получается движение жидкости, близкое к ламинарному. Этот слой называется вязким (иногда «ламинарным») подслоем. Толщина его мала
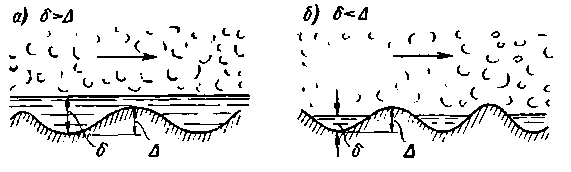
Рис. 4-16. Гладкие (а) и шероховатые (б) русла
(составляет, например, сотые или тысячные доли глубины потока или диаметра трубопровода; на рис. 4-15 толщина ламинарного подслоя преувеличена — показана не в масштабе). Между так называемым турбулентным ядром потока и вязким подслоем имеется тонкий переходной участок, в пределах которого пульсации скоростей резко снижаются.
2°. Гидравлически гладкие и шероховатые трубы. На рис. 4-16 обозначены: Δ – высота выступов шероховатости стенки русла и 𝛿 — толщина вязкого подслоя.
При наличии схемы а выступы шероховатости покрываются (сглаживаются) вязким подслоем (𝛿 > Δ), причем получаем так называемые гладкие стенки (иногда говорят «гидравлически гладкие» стенки). В этом случае потери напора по длине оказываются не зависящими от шероховатости стенок русла.
При наличии схемы б выступы шероховатости не покрываются полностью вязким подслоем (𝛿 < Δ); эти выступы «вклиниваются» (как отдельные «бугорки») в турбулентную зону, и о них могут «ударяться» жидкие частицы турбулентного ядра потока[19]. В этом случае потери напора по длине 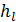 , зависят от шероховатости стенок русла.
, зависят от шероховатости стенок русла.
Особыми исследованиями было установлено, что толщина вязкого подслоя 𝛿 уменьшается с увеличением числа Рейнольдса. Отсюда ясно, что понятия гладкой и шероховатой стенок являются понятиями относительными: одна и та же стенка в одних условиях (при малых Re) может быть «гладкой», в других же условиях (при больших Re) может быть «шероховатой».
3°. Зависимости для построения эпюры осредненных скоростей в случае напорных круглых труб при турбулентном движении. Вопросу о распределении осредненных скоростей по живому сечению турбулентного потока посвящено большое количество теоретических и экспериментальных работ.
Рассмотрим для примера круглоцилиндрическую трубу (см. рис. 4-6).
Для того чтобы получить уравнение кривой АСВ, ограничивающей эпюру осредненных продольных скоростей, выписываем, как и в случае ламинарного движения (см. § 4-4), два разных выражения для касательного напряжения (см. продольный центральный «жидкий столб» на рис. 4-6):
1) уравнение равномерного движения (4-18) в виде
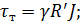
2) уравнение для турбулентного касательного напряжения (4-55)
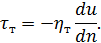
Решая эту систему уравнений, так же как и в случае ламинарного движения, получаем [см. уравнение (4-31)]
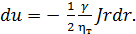 (4-60)
(4-60)
Интегрируя это уравнение, имеем
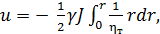 (4-61)
(4-61)
где 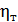 определяется соотношением (4-56).
определяется соотношением (4-56).
В случае ламинарного движения, получив выражение, аналогичное (4-61), имели возможность вынести за интеграл величину η (как величину постоянную для данной жидкости). При этом уравнение (4-61) легко решалось. В случае турбулентного движения величина 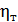 зависит от обстоятельств движения, которые различны для разных величин r. Поэтому для турбулентного движения уравнение (4-61) может быть решено только приближенно в результате использования дополнительных допущений и гипотез. Такая задача была решена Л. Прандтлем, причем им был получен логарифмический закон распределения скоростей по живому сечению круглоцилиндрической напорной трубы. Эту же задачу решали и другие исследователи (Карман, Тейлор, А. Н. Патрашев и др.).
зависит от обстоятельств движения, которые различны для разных величин r. Поэтому для турбулентного движения уравнение (4-61) может быть решено только приближенно в результате использования дополнительных допущений и гипотез. Такая задача была решена Л. Прандтлем, причем им был получен логарифмический закон распределения скоростей по живому сечению круглоцилиндрической напорной трубы. Эту же задачу решали и другие исследователи (Карман, Тейлор, А. Н. Патрашев и др.).
Зависимость Прандтля для гладких труб после введения в нее некоторых эмпирических коэффициентов, найденных И. Никурадзе, имеет вид:
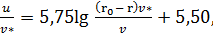 (4-62)
(4-62)
где 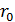 — радиус трубы;
— радиус трубы; 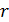 — расстояние от центра живого сечения до точки, где
— расстояние от центра живого сечения до точки, где
определяется скорость u; 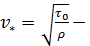 особое обозначение. Зависимость, аналогичная (4-62), была предложена Л. Прандтлем и для шероховатых труб.
особое обозначение. Зависимость, аналогичная (4-62), была предложена Л. Прандтлем и для шероховатых труб.
Величину 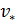 , имеющую размерность скорости, называют скоростью трения или «динамической скоростью»; величину
, имеющую размерность скорости, называют скоростью трения или «динамической скоростью»; величину 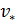 можно найти, исходя из основного уравнения равномерного движения (4-15):
можно найти, исходя из основного уравнения равномерного движения (4-15):
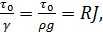
откуда
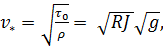 (4-63)
(4-63)
где гидравлический радиус R = D/4.
Полученные для круглоцилиндрических напорных труб полуэмпирические уравнения кривой ABC (рис. 4-17) не лишены некоторых недостатков; они не всегда удовлетворяют пограничным условиям: при r=r0 иногда дают скорость (непосредственно на стенке — в самой близи стенки, где имеется ламинарный подслой) u = -∞; по зависимости Прандтля величина градиента скорости 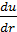 на оси трубы оказывается не равной нулю, что не соответствует
на оси трубы оказывается не равной нулю, что не соответствует
действительности. Вместе с тем эти формулы дают достаточно хорошее совпадение с опытами для основной части ядра потока.
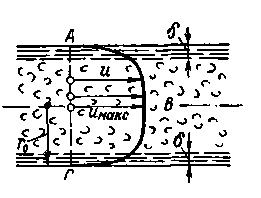
Рис. 4-17. Распределение осреднённых скоростей в круглой трубе при турбулентном движении
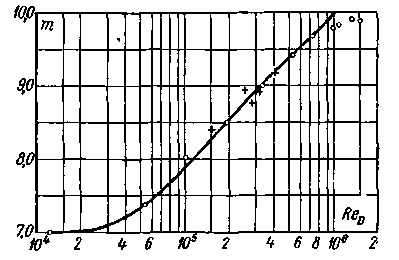
Рис. 4-18. Экспериментальный график для величины m в формуле (4-64)
Практически более удобными являются приближенные формулы, выражающие закон распределения скоростей в виде степенных функций.
Карман (в 1921 г.) на основании теоретических исследований предложил записывать этот закон для гладких труб в виде:[20]
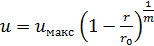 , (4-64)
, (4-64)
где 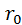 — радиус трубы;
— радиус трубы; 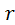 — расстояние от центра живого сечения до точки, где измеряется скорость
— расстояние от центра живого сечения до точки, где измеряется скорость 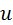 ;m — знаменатель показателя степени, зависящий от числа Рейнольдса
;m — знаменатель показателя степени, зависящий от числа Рейнольдса 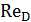 (рис. 4-18);
(рис. 4-18); 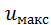 — максимальная скорость (на оси трубы); об
— максимальная скорость (на оси трубы); об 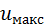 см. § 4-8,
см. § 4-8, 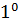 .
.
А. Д. Альтшуль в 1956 г. показал, что зависимость (4-64) действительна не только для гладких, но и для шероховатых труб (т. е. для всей области турбулентного движения), если величину показателя 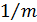 будем находить по формуле (о коэффициенте λ см. ниже § 4-9):[21]
будем находить по формуле (о коэффициенте λ см. ниже § 4-9):[21]
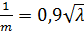 , (4-65)
, (4-65)
4°. Пристенный пограничный слой. Покажем на рис. 4-19 неподвижную горизонтальную пластинку АВ достаточной длины. Далее, рассматривая плоскую задачу, будем считать, что на эту пластинку слева «набегает» горизонтальный поток реальной жидкости, причем эпюра скоростей, построенная для этого потока в вертикальном его сечении О — О (см. рисунок) характеризуется величинами u = const по всей высоте сечения О — О.
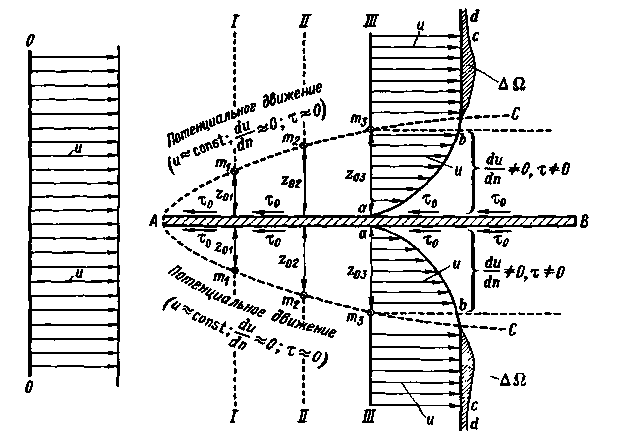
Рис. 4-19. Пристенные пограничные слои толщиной z0 (возникающие у неподвижной пластинки АВ; см. верхнюю и нижнюю области CAB)
Очевидно, реальная жидкость, набегая на пластинку АВ, получает, например, на верхней поверхности этой пластинки[22] касательные напряжения трения 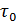 (подтормаживающее движение жидкости), причем непосредственно на данной поверхности пластинки скорость u оказывается равной нулю.
(подтормаживающее движение жидкости), причем непосредственно на данной поверхности пластинки скорость u оказывается равной нулю.
Рассматривая некоторое вертикальное сечение, например, сечение III-III, видим, что в связи с упомянутым подтормаживающим действием пластинки АВ, эпюра скоростей u в данном сечении будет ограничена кривой abed[23].При этом в пределах участка высотой 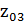 (см. рисунок, участок живого сечения аm3) скорость u для сечения III-III будет изменяться существенно; за пределами же этого участка скорость u будет изменяться пренебрежимо мало, а следовательно, в этой области мы будем иметь (для сечения III-III)
(см. рисунок, участок живого сечения аm3) скорость u для сечения III-III будет изменяться существенно; за пределами же этого участка скорость u будет изменяться пренебрежимо мало, а следовательно, в этой области мы будем иметь (для сечения III-III)
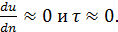
Аналогичная картина будет и в других вертикальных сечениях, например, в сечениях I-I и II-II (см. рисунок). Однако величины 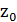 для всех этих сечений будут различны:
для всех этих сечений будут различны:
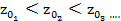
В связи со сказанным, можно наметить некоторую линию АС, выделяющую у стенки слой жидкости, характеризуемый следующим:
1)высота (толщина) этого слоя z0 по течению увеличивается;
2) в пределах его величины 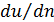 и τ существенно отличаются от нуля;
и τ существенно отличаются от нуля;
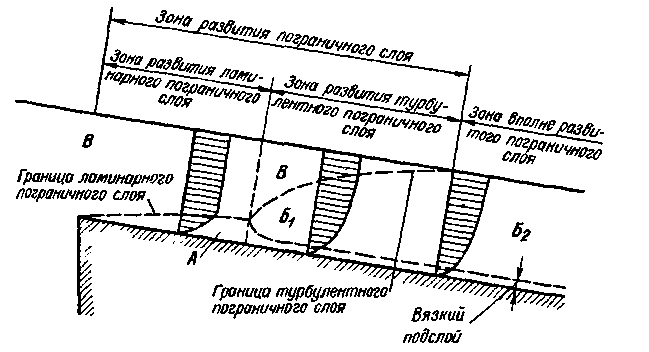
Рис. 4-20. Развитие пристенного пограничного слоя в начале канала
3) за пределами его величины du/dn и τ изменяются (в соответствующих вертикальных сечениях) пренебрежимо мало, и следовательно, за указанными пределами вязкость жидкости можно не учитывать и считать жидкость как бы идеальной,[24] а движение жидкости потенциальным.
Условимся пристенный слой, характеризуемый тремя отмеченными обстоятельствами, называть «пристенным пограничным слоем».
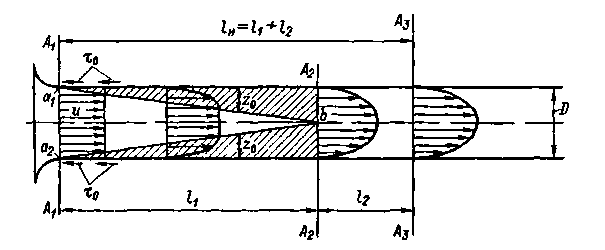
Рис. 4-21. Развитие пристенного пограничного слоя на начальном участке круглой напорной трубы (пограничный слой показан штриховкой); правее вертикали А2-А2, пограничный слой отсутствует
На рис. 4-20, заимствованном из [4-9], дана схема поступления жидкости из большого водоема в канал. На этой схеме показаны: ламинарная часть А пограничного слоя, турбулентная часть Б1 пограничного слоя и, наконец, область В, характеризуемая столь малыми значениями du/dn, что величиной трения в этой области можно пренебречь. Зону В можем рассматривать как область идеальной жидкости и считать, что в ней имеется потенциальное безвихревое движение (см. § 3-4 и 3-5). Трактуя понятие пристенного пограничного слоя несколько иначе, чем то было пояснено нами выше, автор данной схемы область Б2называет «вполне развитым пограничным слоем»» (хотя эта область не удовлетворяет 1-му и 3-му условиям, отмеченным выше).
5°. Развитие пограничного слоя в напорной трубе. «Начальный участок» потока.Если на рис. 4-21 представить поступление реальной жидкости из какого-либо сосуда в круглую трубу, имеющую весьма плавный вход, то в начальном состоянии А1А1трубы будем иметь почти равномерную эпюру скоростей и. Далее на длине l1 (до сечения А2А2) благодаря подтормаживающему действию напряжений трения τ0 (действующих со стороны стенок трубы на жидкость) толщина z0 пограничного слоя начинает увеличиваться по длине грубы (см. рисунок, на котором штриховкой показан пограничный слой, развивающийся в круглой трубе). В сечении А2А2происходит «смыкание» рассматриваемого пограничного слоя (в точке b). Между верхней и нижней частями пограничного слоя на длине l1 показана незаштрихованная область a1 — b — а2; внутри этой области имеем потенциальное движение жидкости: в любом вертикальном сечении этой области скорости и = const (однако, по течению эти скорости увеличиваются).
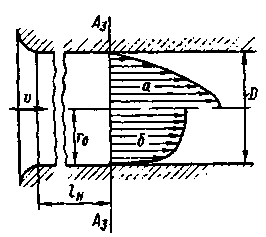
Рис. 4-22. Эпюры скоростей в конце начального участка: а — ламинарный режим, б —турбулентный режим
Рассматривая рис. 4-21, следует различать помимо участка, где располагается пограничный слой, еще участок потока длиной l2(между сечениями А2А2и А3А3). В пределах этого участка происходит:
а) переформирование эпюры скоростей и, получившейся в сечении А2А2, в эпюру скоростей (показанную в сечении А3А3), свойственную равномерному движению;
б) изменение уровня пульсации скоростей до уровня, свойственного равномерному движению.
«Начальным участком» трубопровода следует называть участок длиной
ln — li 12; на длине этого участка мы имеем неравномерное движение. Важно подчеркнуть, что приводимые ниже расчетные зависимости, служащие для определения потерь напора hhне могут быть, строго говоря, приемлемы для начального участка, где мы не имеем равномерного движения.
Выше мы говорили о турбулентном движении; надо учитывать, что аналогичный участок («начальный участок») должен иметь место и при ламинарном режиме.
Длина начального участка ln для круглых труб (согласно экспериментальным данным) может быть принята (для турбулентного движения)
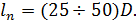 (4-66)
(4-66)
На рис. 4-22 представлены эпюры, сформировавшиеся в конце начальною участка (в сечении А3А3) при ламинарном и при турбулентном движении. Как видно, максимальная толщина пограничного пристенного слоя в напорной круглой трубе (имеющая место в сечении А3А3) равна половине диаметра трубы.
§
§ 4-9. ФОРМУЛА ВЕЙСБАХА – ДАРСИ КОЭФФИЦИЕНТ
ГИДРАВЛИЧЕСКОГО ТРЕНИЯ λ
Как показывают опыты, величина 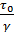 (см. § 4-2) может быть выражена через скоростной напор следующим образом:[25]
(см. § 4-2) может быть выражена через скоростной напор следующим образом:[25]
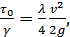 (4-67)
(4-67)
где λ/4 — некоторый эмпирический коэффициент пропорциональности.
Сопоставляя (4-67) с (4-15), можем написать:
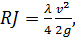 (4-68)
(4-68)
откуда, учтя, что J = hl:l, получаем следующую общую зависимость для потерь напора по длине при равномерном установившемся движении:
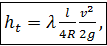 (4-69)
(4-69)
где l — длина потока; R — гидравлический радиус.
Для круглых напорных труб D = 4R, и потому для этих труб общая зависимость (4-69) переписывается в виде:
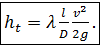 (4-70)
(4-70)
Формула (4-70) называется формулой Вейсбаха — Дарcи. Безразмерный коэффициент λ, входящий в нее, будем именовать коэффициентом гидравлического трения.
В случае ламинарного напорного движения жидкости в круглой трубе мы уже получили выше теоретическую формулу (4-46) для λ. При турбулентном течении λ находится по эмпирическим формулам.
Ранее считали, что коэффициент λ, входящий в выражение (4-70), является постоянной величиной; несколько позже его ставили в зависимость от средней скорости v или диаметра D. Некоторые авторы связывали величину λ только с шероховатостью стенок труб. Такого рода зависимости в настоящее время считаются устаревшими и неприемлемыми в практике.
Современные расчетные формулы для λ предусматривают зависимость этого коэффициента в общем случае только от шероховатости стенок русла и от числа Рейнольдса. Величину λ в случае круглых труб можно найти для турбулентного движения (так же как и для ламинарного движения; см. выше), зная закон распределения скоростей по живому сечению.
Действительно, формулу (4-70) можно переписать в виде
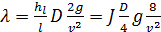 (4-71)
(4-71)
и затем, учтя (4-63), в виде
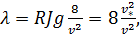 (4-72)
(4-72)
откуда
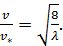 (4-73)
(4-73)
Выражение для 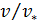 можно найти из (4-62). Подставляя такое выражение в (4-73), нетрудно найти зависимость для величины λ.
можно найти из (4-62). Подставляя такое выражение в (4-73), нетрудно найти зависимость для величины λ.
Л. Прандтль в 1932 г. для гладких труб получил следующую формулу (исходя из некоторой неполной воображаемой модели):
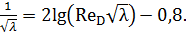 (4-74)
(4-74)
Блазиус в 1913 г. на основании обработки многочисленных опытов по исследованию движения жидкости в круглых гладких (латунных) трубах при числах Рейнольдса ReD от 4000 до 100000 установил эмпирическую зависимость
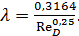 (4-75)
(4-75)
Формулы для 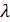 в случае шероховатых труб были предложены многими авторами. Прежде чем остановиться на пояснении тех из них, которые в настоящее время главным образом должны рекомендоваться для практического применения, осветим (в следующем параграфе) работу И. Никурадзе, обобщившего при помощи особого графика результаты всех исследований в области вопроса о потерях напора в круглых трубах.
в случае шероховатых труб были предложены многими авторами. Прежде чем остановиться на пояснении тех из них, которые в настоящее время главным образом должны рекомендоваться для практического применения, осветим (в следующем параграфе) работу И. Никурадзе, обобщившего при помощи особого графика результаты всех исследований в области вопроса о потерях напора в круглых трубах.
§ 4-10. ИССЛЕДОВАНИЯ И. НИКУРАДЗЕ. ОБОБЩЕНИЕ ВОПРОСА О ПОТЕРЯХ НАПОРА
Представим на рис. 4-23 трубу диаметром D с задвижкой К и двумя пьезометрами П. При помощи задвижки К можно изменять скорость v в трубе, причем для каждой такой скорости, установившейся в трубе, можно по пьезометрам определять (в случае установившегося движения) потерю напора  на участке трубы длиной l.
на участке трубы длиной l.
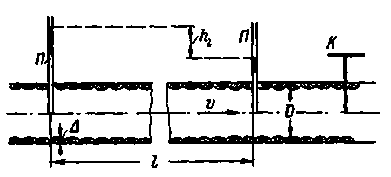
Рис. 4-23. Схема опытов Никурадзе
Коэффициент гидравлического трения λ. согласно формулам (4-70) и (3-135), можно выразить через ReD:
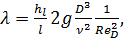
причем по этой формуле, определив а опытов величины  ,
,  и ν, можно вычислять значения λ = f(ReD).
и ν, можно вычислять значения λ = f(ReD).
Проводя подобные опыты, И. Никурадзе исследовал (в 1933 г.) запорные круглоцилиндрические трубы, имеющие однозернистую равномерно распределенную искусственную шероховатость, которую он создавал, наклеивая на стенки трубы песчинки одинаковой высоты Δ на одинаковом расстоянии друг от друга. Результаты своих опытов Никурадзе представил в виде особого графика, по осям которого он отложил безразмерные величины λ и ReD, причем на таком графике был нанесен ряд кривых, вычисленных в соответствии с приведенной выше зависимостью; каждая кривая отвечала определенной так называемой относительной шероховатости:
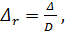 (4-76)
(4-76)
где Δ можно назвать «высотой выступов шероховатости» (будем считать, что размер Δ весьма мал сравнительно с диаметром D).
Этот график (см. далее рис. 4-24) позволил в удобной форме обобщить вопрос о потерях напора (в случае равномерного установившегося движения несжимаемой жидкости в круглой трубе) и наглядно показать следующее:
1) коэффициент λ, входящий в формулы (4-69) и (4-70), в самом общем случае зависит только от 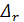 и ReD;
и ReD;
2) имеются частные случаи движения жидкости, когда λ зависит или только от 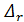 , или только от ReD;
, или только от ReD;
3) имеются вполне определенные зоны сочетания λ и ReD, для которых в формулах, выражающих пропорциональность (::) 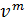 величине
величине 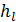 ,
,
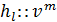 (4-77)
(4-77)
показатель степени m приобретает вполне определенное значение (равное единице, двум и т.п.).
На рис. 4-24 показана схема графика Никурадзе. Пользуясь ею, поясним основные положения, вытекающие из рассмотрения данного графика, на котором показаны две «опорные» прямые: прямая I, построенная по уравнению (4-46) (см. линию 1 – 2 – 3); эта прямая называется прямой ламинарного режима; прямая II, построенная исходя из уравнения Блазиуса (4-75); назовем ее прямой Блазиуса.
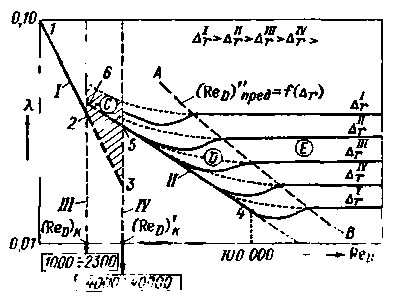
Рис. 4-24. Схема графика Никурадзе (кривые λ =f(ReD) для различных 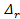 ,) I – зона ламинарного режима, С – зона неустойчивого (переходного) режима, II – область гладких русел турбулентной зоны, D – область доквадратичного сопротивления шероховатых русел турбулентной зоны, Е – область квадратичного сопротивления шероховатых русел турбулентной зоны
,) I – зона ламинарного режима, С – зона неустойчивого (переходного) режима, II – область гладких русел турбулентной зоны, D – область доквадратичного сопротивления шероховатых русел турбулентной зоны, Е – область квадратичного сопротивления шероховатых русел турбулентной зоны
Откладывая в соответствующем масштабе по осям графика величины lgReD (по горизонтальной) и lgλ, (по вертикальной), мы на шкалах осей выписываем сами числа ReD и λ (а не величины их логарифмов). Построение графика в таких логарифмических координатах позволяет «опорные» линии I и II, выражаемые степенными функциями, представить в виде прямых.
Все поле графика можно разбить на три зоны:
Первая зона – зона ламинарного режима; она представлена отрезком прямой 1-2, построенной по уравнению (4-46). Здесь экспериментальные кривые
λ = f(ReD), найденные для разных 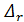 , сливаются в одну прямую линию, совпадающую с линией 1-2.
, сливаются в одну прямую линию, совпадающую с линией 1-2.
Для этой зоны имеем следующее:
а) величины ReD относительно малы, менее (ReD)K = 1000 ÷ 2300 [см. формулу (3-136)];
б) потеря напора 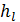 не зависит от шероховатости, так как все кривые
не зависит от шероховатости, так как все кривые
λ = f(ReD), построенные для разных 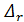 , как то было отмечено, сливаются
, как то было отмечено, сливаются
в одну прямую 1 – 2;
в) потери напора прямо пропорциональны первой степени скорости 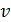
[как то следует из формул (4-45) и (4-46); в данном случае показатель
степени m = 1];
г) величина λ определяется формулой (4-46).
Вторая зона – зона, расположенная между вертикалями III и IV (заштрихована), является зоной неустойчивого режима (см. § 3-24; зону (3) на рис. 3-42). Ее называют, как было отмечено выше, неустойчивой или переходной зоной (зоной, внутри которой происходит переход ламинарного режима в турбулентный и наоборот – турбулентного режима в ламинарный). Здесь:
а) числа Рейнольдса лежат в пределах от 1000 ÷ 2300 до 4000 ÷ 40000;
б) при движении жидкости по трубе на отдельных участках возникают
отдельные области турбулентного режима, которые разрастаются, а затем
исчезают и снова появляются. В связи с этим данная зона иногда называется
зоной перемежающейся турбулентности.
Заметим, что когда турбулентные области в трубе разрастаются, растет и сопротивление движению жидкости (в связи с ростом турбулентных касательных напряжений трения), при этом скорость 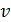 уменьшается. Как только она делается меньше критической скорости, разросшиеся турбулентные области обращаются в ламинарные (или выносятся за пределы рассматриваемой части потока); после этого в связи с уменьшением потерь напора (обусловленным переходом турбулентного режима в ламинарный на отдельных участках трубы) скорость
уменьшается. Как только она делается меньше критической скорости, разросшиеся турбулентные области обращаются в ламинарные (или выносятся за пределы рассматриваемой части потока); после этого в связи с уменьшением потерь напора (обусловленным переходом турбулентного режима в ламинарный на отдельных участках трубы) скорость 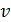 увеличивается, причем турбулентные области снова появляются и т. д. В связи с таким характером движения в переходной зоне, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение здесь могут составить только случаи, когда ламинарный режим «затягивается» и имеет место по длине всего трубопровода (см. прямую 2 – 3) или, когда в связи с особыми условиями движения турбулентный режим имеет место по длине всего трубопровода (см. линию 5 – 6).
увеличивается, причем турбулентные области снова появляются и т. д. В связи с таким характером движения в переходной зоне, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение здесь могут составить только случаи, когда ламинарный режим «затягивается» и имеет место по длине всего трубопровода (см. прямую 2 – 3) или, когда в связи с особыми условиями движения турбулентный режим имеет место по длине всего трубопровода (см. линию 5 – 6).
Дополнительно надо иметь в виду еще следующее обстоятельство, которое может затруднять определение потерь напора (и, следовательно, величин λ) для области неустойчивого режима.
Можно допустить, что при Q = const (а следовательно, и при 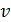 = const) кинетическая энергия жидкости, находящейся в трубе (между рассматриваемыми пьезометрами; рис. 4-23) при турбулентном и ламинарном режимах является различной по величине. Такое положение обусловливается тем, что коэффициент α при ламинарном и турбулентном режимах имеет различное значение, кроме того, при турбулентном режиме происходит пульсация скоростей. В указанном случае при смене режимов разность показаний пьезометров не будет равна искомой потере напора
= const) кинетическая энергия жидкости, находящейся в трубе (между рассматриваемыми пьезометрами; рис. 4-23) при турбулентном и ламинарном режимах является различной по величине. Такое положение обусловливается тем, что коэффициент α при ламинарном и турбулентном режимах имеет различное значение, кроме того, при турбулентном режиме происходит пульсация скоростей. В указанном случае при смене режимов разность показаний пьезометров не будет равна искомой потере напора 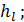 она будет равна величине
она будет равна величине 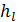 плюс соответствующий так называемый инерционный напор (поясняемый далее в гл. 9), который определить в данном случае нет возможности.
плюс соответствующий так называемый инерционный напор (поясняемый далее в гл. 9), который определить в данном случае нет возможности.
Третья зона – зона турбулентного режима; эта зона располагается правее вертикали IV, отвечающей ReD ≈ 4000 ÷ 40000. Данная зона в свою очередь разбивается на три области.
Первая область – «область гладких русел»; она представлена: а) при числах Рейнольдса ReD < 100000 – прямой линией II и б) при числах Рейнольдса ReD > 100000 – кривой линией, являющейся продолжением прямой II; данная кривая, начинающаяся от точки 4, на. рис. 4-24 не показана (она будет представлена далее на рис. 4-25 в виде самой нижней кривой линии). Для первой области имеем:
a) 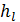 в пределах до чисел ReD= 100000 прямо пропорционально скорости
в пределах до чисел ReD= 100000 прямо пропорционально скорости 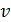 в степени 1,75 (m = 1,75), как то следует из формул (4-70) и (4-75);
в степени 1,75 (m = 1,75), как то следует из формул (4-70) и (4-75);
б) h, не зависит от шероховатости, поскольку все кривые Δr= const сливаются в одну линию (здесь мы получаем гладкие трубы; выступы шероховатости покрыты ламинарным подслоем);
в) htа также X, зависит только от числа Рейнольдса, согласно формуле Блазиуса (4-75) или Прандтля (4-74),
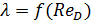 (4-78)
(4-78)
Вторая область — «область доквадратичного сопротивления шероховатых русел», эта область лежит между прямой II и линией АВ.

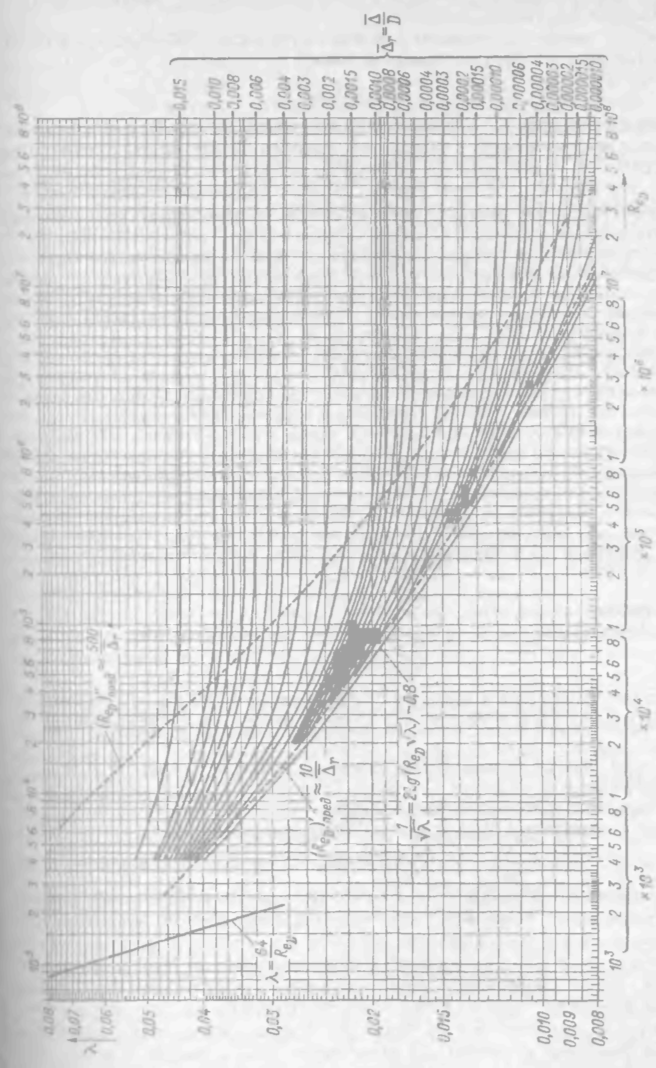
Согласно Никурадзе, кривые Δr = const в этой области имеют вид, показанный сплошными линиями; согласно опытам ряда других авторов, эти кривые имеют другой вид (см. штриховые линии). Такое расхождение объясняют различием геометрических форм шероховатости, имевшей место при проведении опытов. Считают, что кривые Никурадзе относятся к однозернистой равномерно распределенной шероховатости; штриховые же кривые — к шероховатости разнозернистой, свойственной, например, стальным и чугунным трубам.
Из сказанного выше ясно, что на левой границе рассматриваемой области кривые графика, опускаясь вниз, характеризуются в месте отрыва их от опорной прямой II показателем степени т, входящим в формулу (4-77), равным 1,75 На правой границе АВ области, где кривые графика переходят в горизонтальные прямые, m = 2,0 (см. ниже). Можно показать, что поднимающиеся кверху сплошные линии Никурадзе (расположенные внутри рассматриваемой области), характеризуются показателем степени т > 2,0. Отсюда заключаем, что т в пределах данной области изменяется от 1,75 до 2,0, причем для однозернистой равномерно распределенной шероховатости этот показатель, согласно Никурадзе, в промежутке между т = 1,75 и т = 2,0 должен иметь максимум (тмакс > 2,0); для разнозернистой же шероховатости, по данным других авторов, показатель т в пределах данной области монотонно возрастает от 1,75 до 2,0.
Из графика видно, что для данной области λ, а также hlзависят как от числа Рейнольдса, так и от относительной шероховатости:
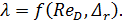 (4-79)
(4-79)
Третья область — «область квадратичного сопротивления шероховатых русел»; эта область располагается правее линии АВ. Здесь:
а) потеря напора прямо пропорциональна квадрату скорости v (т = 2,0);
б) коэффициент X не зависит от числа Рейнольдса ReD (все линии
графика — прямые, параллельные горизонтальной оси);
в) hl и λ зависят от относительной шероховатости:
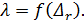 (4-80)
(4-80)
В заключение необходимо отметить, что общий качественный характер связей, полученный Никурадзе для круглоцилиндрических напорных труб, разумеется, можно распространить и на потоки другого вида (напорные и безнапорные). Важно подчеркнуть, что после работы Никурадзе стало совершенно ясно, что при выполнении любых гидравлических расчетов нет надобности различать жидкости разного вида (как то делали ранее, когда предлагали отдельные расчетные формулы для вычисления потерь напора в случае воды, нефти, разных масел и т. п.). Именно из рассмотрения графика Никурадзе делается очевидным, что в гидравлике при определении потерь напора следует иметь в виду жидкость вообще, движение которой характеризуется безразмерным числом Рейнольдса определенной величины (зависящим, в частности, от таких физических характеристик рассматриваемой жидкости, как ее коэффициент вязкости и ее плотность).
§
Как было отмечено выше, различают шероховатые трубы, имеющие однозернистую шероховатость (с которыми работал Никурадзе) и трубы, имеющие разнозернистую шероховатость (когда выступы шероховатости имеют неодинаковую форму и размеры, расстояние между ними также различно). Трубы, обычно встречающиеся в практике, так называемые технические, имеют разнозернистую шероховатость или являются гладкими. Ниже поясним расчет технических труб.
1°. Напорные шероховатые технические трубы (трубы с разнозернистой шероховатостью). Для этих труб в 1938 г. Кольбрук на основании своих опытов, а также с учетом исследований других авторов, предложил формулу:
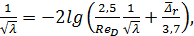 (4-81′)
(4-81′)
где 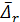 — осредненная относительная шероховатость [см. формулу (4-76)]. По этой формуле был построен график[26] (рис. 4-25). Пользуясь этим графи-ком, можно определить коэффициент λ в случае технических труб для всех трех областей турбулентной зоны.
— осредненная относительная шероховатость [см. формулу (4-76)]. По этой формуле был построен график[26] (рис. 4-25). Пользуясь этим графи-ком, можно определить коэффициент λ в случае технических труб для всех трех областей турбулентной зоны.
Для квадратичной области сопротивления шероховатых труб формула (4-81′) упрощается и приобретает вид формулы Прандтля (предложенной им для шероховатых труб):
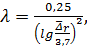 (4-81′′)
(4-81′′)
Для технических труб под величиной 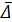 понимают некоторую среднюю высоту выступов шероховатости. Такую осредненную геометрическую характеристику
понимают некоторую среднюю высоту выступов шероховатости. Такую осредненную геометрическую характеристику 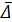 установить для рассматриваемой трубы путем непосредственного измерения выступов шероховатости нельзя. Поэтому при определении среднего значения
установить для рассматриваемой трубы путем непосредственного измерения выступов шероховатости нельзя. Поэтому при определении среднего значения 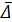 для данной трубы поступают следующим образом.
для данной трубы поступают следующим образом.
Рассматривают квадратичную область сопротивления и для этой области опытным путем, пользуясь формулой (4-70), находят для данной трубы величину λ. Затем по формуле (4-81“) вычисляют искомое значение.  Найденное таким образом среднее значение
Найденное таким образом среднее значение 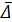 называют эквивалентной шероховатостью.
называют эквивалентной шероховатостью.
Эквивалентная шероховатость зависит: а) от материала и способа изго-товления и соединения труб, б) от продолжительности эксплуатации труб, в процессе которой могут возникнуть коррозия стенок или инкрустации (образование наростов на стенках). Численные значения эквивалентной шероховатости 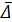 , найденные указанным путем для разных труб, приводятся в табл. 4-2. По этой таблице и определяют
, найденные указанным путем для разных труб, приводятся в табл. 4-2. По этой таблице и определяют 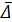 при выполнении практических расчетов.
при выполнении практических расчетов.
Таблица 4-2
Шероховатость  труб и каналов[27]
труб и каналов[27]
| Характеристика поверхности труб и каналов |  , мм , мм |
| I. Цельнотянутые трубы | |
| Из латуни …………………………………………………………………….. | 0,0015-0,0100 |
| Новые стальные …………………………………………………………… | 0,020-0,100 |
| Стальные водопроводные, находящиеся в эксплуатации.. | 1,20-1,50 |
| II. Цельносварные стальные трубы | |
| Новые или старые в хорошем состоянии ………………………. | 0,04-0,10 |
| Бывшие в эксплуатации ……………………………………………….. | ≈ 0,10-0,15 |
| С двойной поперечной клепкой, сильно корродированные | 2,0 |
| III. Чугунные трубы | |
| Новые…………………………………………………………………………… | 0,25-1,00 |
| Новые битумизированные…………………………………………….. | 0,10-0,15 |
| Асфальтированные……………………………………………………….. | 0,12-0,30 |
| Бывшие в эксплуатации, корродированные…………………… | 1,0-1,5 |
| IV. Бетонные и асбестоцементные трубы | |
| Бетонные трубы при хорошей поверхности с затиркой….. | 0,3-0,8 |
| Бетонные трубы при среднем качестве работ…………………. | 2,5 |
| Бетонные трубы с грубой (шероховатой)поверхностью…. | 3,0-9,0 |
| Асбестоцементные трубы новые…………………………………… | 0,05-0,10 |
| Асбестоцементные трубы, бывшие в эксплуатации……….. | ≈0,60 |
| V. Деревянные и стеклянные трубы | |
| Деревянные трубы из тщательно остроганных досок…….. | 0,15 0,30 0,70 |
| Деревянные трубы из хорошо отстроганных досок………… | |
| Деревянные трубы из нестроганных хорошо пригнанных досок…………………………………………………………………………….. | |
| Трубы из чистого стекла……………………………………………….. | 0,0015-0,0100 |
| VI. Облицовка каналов | |
| Хорошая штукатурка из чистого цемента………………………. | 0,05-0,22 |
| Штукатурка цементным раствором с ожелезнением………. | 0,5 |
| Штукатурка по металлической сетке……………………………… | 10-15 |
| Шлакобетонные плиты…………………………………………………. | 1,5 |
Зная для данной трубы 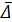 , находим по (4-76) значение
, находим по (4-76) значение 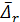 ; затем по формуле (3-135) определяем ReD. Имея для рассматриваемой трубы
; затем по формуле (3-135) определяем ReD. Имея для рассматриваемой трубы 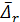 , и ReD, можем найти λ по графику на рис. 4-25 или по формулам (4-81).
, и ReD, можем найти λ по графику на рис. 4-25 или по формулам (4-81).
Формула (4-81′)неудобна для вычисления (величину λ по этой формуле приходится находить подбором). А. Д. Альтшуль предложил вместо зависимости (4-81′) более простую формулу:
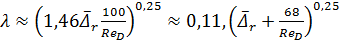 , (4-82′)
, (4-82′)
которая для квадратичной области сопротивления приводится к формуле Шифринсона:
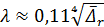 , (4-82′′)
, (4-82′′)
этой последней формулой можно пользоваться вместо формулы (4-81′) только при 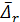 < 0,007.
< 0,007.
В случае прямоугольных труб с соотношением сторон поперечного сечения, лежащем в пределах от 0,5 до 2,0, величина λ может определяться также по приведенному графику или по формулам (4-81) и (4-82); здесь только под D надо понимать так называемый гидравлический диаметр
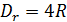 , (4-83)
, (4-83)
где R — гидравлический радиус рассматриваемой прямоугольной трубы (заметим, что для круглой трубы гидравлический диаметр оказывается равным геометрическому диаметру: Dr = D).
Обратим внимание, что на рис. 4-25 нанесены две пунктирные кривые, выделяющие область доквадратичного сопротивления, характеризующуюся зависимостью (4-79). Числа Рейнольдса, отвечающие этой области, лежат в пределах
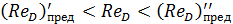 (4-84)
(4-84)
В случае
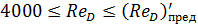 (4-85)
(4-85)
получаем область, которую практически следует рассматривать как область гладких труб (см. ниже п. 2°), для которых практически действует зависимость (4-78). В случае же
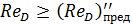 (4-86)
(4-86)
имеем квадратичную область сопротивления, для которой справедлива зависимость (4-80).
Согласно А. Д. Альтшулю, предельные числа Рейнольдса 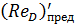 и
и 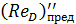 с некоторым приближением могут быть найдены по формулам:
с некоторым приближением могут быть найдены по формулам:
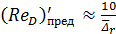 ; (4-87)
; (4-87)
 (4-88)
(4-88)
Пользуясь приведенными зависимостями, можно решить вопрос о том:
а) когда данная труба должна рассматриваться как практически гладкая и ее можно рассчитывать, не считаясь с выступами шероховатости;
б) когда данную трубу следует рассчитывать по зависимостям, относящимся к области квадратичного сопротивления, не считаясь с величиной чисел Рейнольдса.
Не следует смешивать критические числа Рейнольдса (нижнее и верхнее) с предельными числами Рейнольдса, выделяющими область доквадратичного сопротивления.
2°. Напорные гладкие технические трубы. В этом случае формулы
(4-81′) и (4-82“) упрощаются и приобретают вид уже известных нам формул Прандтля (4-74) и Блазиуса (4-75). Как уже отмечалось, формула (4-75) дает достаточно точные результаты в случае
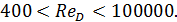 (4-89)
(4-89)
При любых ReD > 4000 можно пользоваться формулой (4-74) или более простой зависимостью, предлагаемой рядом авторов:
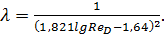 (4-90)
(4-90)
Расчет прямоугольных гладких труб выполняется так, как указано в п. 1°.
3°. Дополнительные замечания. Вслучае стальных и чугунных водопроводных труб, уже находившихся в эксплуатации, величину X в последнее время рекомендуют иногда определять по эмпирическим формулам Ф. А. Шевелева:
а) при ReD ≥ 9,2 • 105 (квадратичная область сопротивления)
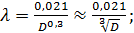 (4-91)
(4-91)
б) при ReD ≤ 9,2 • 105 (доквадратичная область сопротивления)
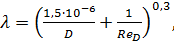 (4-92)
(4-92)
где D всюду выражается в метрах.
В случае расчета стальных труб со сварными стыками, при которых образуются наплывы металла, иногда дополнительно учитывают по различным эмпирическим формулам (здесь не приводим) влияние этих стыков на величину λ.
В заключение обратим внимание на следующее.
Как видно из графиков рис. 4-24 и 4-25, для квадратичной области сопротивления величина λ не зависит от ReD. Имея это в виду и рассматривая напорное движение в некоторой трубе, длиной l0 = const и диаметром D = const при расходе Q = const, а следовательно, и при скорости v = const, можем заключить, что для этой трубы, согласно упомянутым графикам, с уменьшением вязкости (т. е. с уменьшением v) число Реинольдса ReD будет расти; вместе с тем потери напора (несмотря на уменьшение вязкости) будут оставаться, согласно формуле (4-70), постоянными.
Такой парадокс, по-видимому, можно объяснить следующим образом. С уменьшением v характер турбулентности будет изменяться: она, надо полагать, будет развиваться все более и более; при этом длины путей пробега l отдельными частицами жидкости (от начального сечения 1 – 1 до конечного сечения потока 2 – 2, т. е. от начала трубы до ее конца) должны увеличиваться: длина пробега (длины траекторий) l будет все больше и больше отличаться от длины трубы l0 (l > l0); равным образом должны как-то изменяться и величины относительных перемещений (Δl )отдельных струек по отношению друг к другу. По-видимому, следует считать, что для квадратичной области сопротивления мы должны получать как бы такое равенство ( 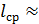 const, где
const, где 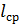 — средняя длина пробега частицами жидкости от начала трубы до ее конца;
— средняя длина пробега частицами жидкости от начала трубы до ее конца; 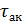 — среднее актуальное касательное напряжение вдоль
— среднее актуальное касательное напряжение вдоль 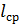 (зависящее, разумеется, от величин Δl).
(зависящее, разумеется, от величин Δl).
Как видно, получается следующая картина: с уменьшением v уменьшается 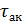 ; но зато, в связи с изменением характера турбулентности увеличивается (
; но зато, в связи с изменением характера турбулентности увеличивается ( 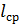 ), причем отмеченное выше произведение (
), причем отмеченное выше произведение ( 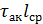 ), от которого должны зависеть потери напора, сохраняет свою величину.
), от которого должны зависеть потери напора, сохраняет свою величину.
Дополнительно надо иметь в виду, что в момент, когда v обращается в нуль, мы получаем идеальную (а следовательно, воображаемую) жидкость, при возникновении которой скорость на стенке русла «скачком» должна измениться от нуля (в случае реальной жидкости) до соответствующей конечной величины (u= const по живому сечению) — в случае идеальной жидкости. При этом здесь получится (при λ = 0) или воображаемый турбулентный поток идеальной жидкости, или воображаемый ламинарный поток идеальной жидкости.
Разумеется, описанный «парадокс» может быть также осознан, исходя из рассмотрения не действительной картины движения жидкости (которую мы имели в виду выше), а из рассмотрения «модели осредненного потока».[28]
Примеры расчета.[29]
№ 1. Дана цельносварная цилиндрическая стальная труба круглого поперечного сечения, бывшая в употреблении, но в хорошем состоянии. Диаметр трубы D = 120 мм: длина ее l = 500 м. По трубе движется керосин, имеющий температуру t = 150С; расход керосина Q = 6 л/с = 0,006 м3/с.
Требуется:
а) установить режим движения керосина в трубе;
б) если режим движения керосина турбулентный, то определить область сопротивления, отвечающую заданным условиям движения;
в) найти величину потерь напора 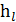 , по длине для заданного трубопровода.
, по длине для заданного трубопровода.
Решение. Шероховатость стенок трубы, согласно табл. 4-2, Δ = 0,04мм.
Относительная шероховатость трубы
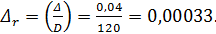
Кинематический коэффициент вязкости для керосина при температуре 150С, согласно табл. 4-1, v = 0,027 см2/с.
Средняя скорость движения керосина в трубе
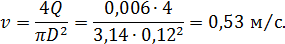
Число Рейнольдса
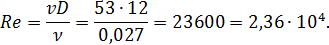
Предельные числа Рейнольдса, согласно формулам (4-87) и (4-88),
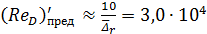 ;
; 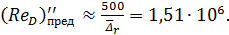
Сопоставляя величину ReD с предельными числами Рейнольдса, видим, что 4000 < ReD < 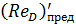 , где 4000 — число Рейнольдса, отвечающее началу турбулентной зоны.
, где 4000 — число Рейнольдса, отвечающее началу турбулентной зоны.
Таким образом, в нашем случае должен иметь место турбулентный режим, относящийся к области гладких русел.
Согласно графику на рис. 4-25, для найденных Δr и ReD величина λ = 0,025.
По формуле Блазиуса (4-75):
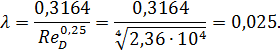
Потеря напора
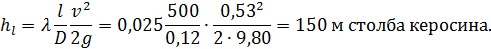
№ 2. Для тех же условий, что и в предыдущем примере (для движения в трубе керосина), определить коэффициент λ и потерю напора на заданном участке трубопровода, если Q = 40 л/с.
Решение. Средняя скорость
 .
.
Число Рейнольдса
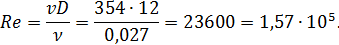
Сопоставляя это число с предельными чисчами Рейнольдса, найденными в предыдущем примере, видим, что
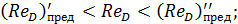
отсюда заключаем, что в данном случае будем иметь область доквадратичного сопротивления турбулентной зоны.
Для найденного ReD и установленной в предыдущем примере Δг, согласно графику рис. 4-25,
λ = 0,0186
Значение λ по формуле (4-81′) получается
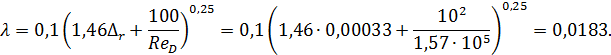
Потеря напора hlпо длине заданного трубопровода
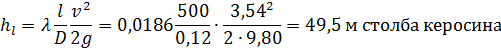
№ 3. Дана круглая цельносварная стальная труба, бывшая в эксплуатации, характеризуемая величиной Δ = 0,15 мм. Диаметр трубы D = 0,5 м: длина ее l = 500 м. По трубе движется вода, имеющая температуру 50 С. Расход воды Q = 0,60 м3/с
Требуется найти потерю напора по длине трубы.
Решение. Относительная шероховатость трубы
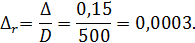
Кинематический коэффициент вязкости для воды заданной температуры, согласно табл. 4-1, v = 0,00556 см2/с.
Средняя скорость движения воды в трубе
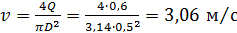 .
.
Число Рейнольдса
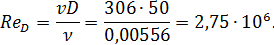
Предельные числа Рейнольдса, согласно формулам (4-87) и (4-88),
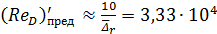 ;
; 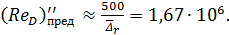
Сопоставляя величину ReD с предельными значениями чисел Рейнольдса, видим, что
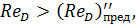
т. е. в данном случае имеет место область квадратичного сопротивления турбулентной зоны. Для найденных Δr и ReD, согласно графику рис. 4-25, λ, = 0.015.
Значение λ по формуле (4-82′) оказывается
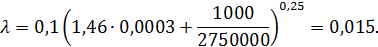
Искомая потеря напора
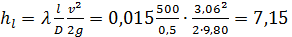 м столба воды, имеющей температуру 50° С.
м столба воды, имеющей температуру 50° С.
§
При проектировании гидротехнических сооружений обычно сталкиваются с квадратичной областью сопротивления, когда вода имеет достаточно большие скорости, при которых числа Рейнольдса получаются также достаточно большими.
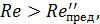 (4-92)
(4-92)
где 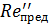 имеет тот же смысл, что и
имеет тот же смысл, что и 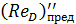 в предыдущем параграфе.
в предыдущем параграфе.
Очень часто при условии, когда неравенство (4-93) несколько нарушается, т. е. когда мы, строго говоря, получаем доквадратичную область сопротивления, практические расчеты все же ведут по зависимостям, относящимся к квадратичной области. Это объясняется тем, что расчет для области квадратичного сопротивления является значительно более простым, чем для области доквадратичного сопротивления. Действительно, для доквадратичной области коэффициент λ, входящий в формулу (4-69), зависит от Re, а следовательно, и от скорости v, которая часто заранее неизвестна. В связи с этим задачи для доквадратичной области обычно приходится решать путем подбора или методом последовательного приближения. В случае же области квадратичного сопротивления λ не зависит от Re, а следовательно, λмы можем найти, не зная величины v, что обычно позволяет решать задачи непосредственно, без подбора. Вместе с тем погрешность в определении величины λ, обусловленная пренебрежением влияния на нее числа Re (когда мы находимся в доквадратичной области), часто может быть значительно меньше той погрешности, которая получается за счет неточности установления величины Δ: как мы видели, шероховатость Δ приходится устанавливать по таблице, где этот параметр определяется на основании чисто описательных, качественных (а не количественных) характеристик русла.
Перечисленные обстоятельства заставляют в гидротехнической практике интересоваться главным образом областью квадратичного сопротивления; исключение здесь составляют только следующие случаи:
а) движение грунтовой воды, когда мы получаем ламинарный режим (см. гл. 17 и 18);
б) движение воды через модели сооружений (см. гл. 16);
в) редкие случаи русел большого поперечного сечения с весьма гладкими (например, стальными) стенками.
Учитывая сказанное, далее, как правило, будем иметь в виду только квадратичную область сопротивления. В настоящем параграфе применительно к этой области сопротивления рассмотрим напорное и безнапорное равномерные движения воды в цилиндрических руслах так называемого «правильного поперечного сечения» (см. начало § 4-2).
Отметим, что к «правильным руслам» относятся русла, имеющие поперечные сечения круглые, квадратные, прямоугольные, трапецеидальные, параболические и т. п. (при условии, что смоченная поверхность этих русел имеет однородную — одинаковую шероховатость). Такие сечения, как, например, звездообразные (встречающиеся в практике машиностроения), характеризующиеся наличием острых углов, мы здесь не будем рассматривать.
Имея в виду только равномерное движение (см. § 3-11), также исключим из рассмотрения движение воды на начальных участках цилиндрических русел (рис. 4-21), поскольку для этих участков эпюры скоростей в живых сечениях имеют особый вид, отличный от вида, свойственного равномерному потоку (следовательно, для этих участков и закон сопротивления движению воды будет иной).
1°. Формула Шези.Перепишем зависимость (4-69) в – виде
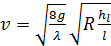 (4-94)
(4-94)
или в виде
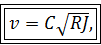 (4-95)
(4-95)
где v — средняя скорость в данном живом сечении; R — гидравлический радиус; J — пьезометрический уклон, равный в рассматриваемом случае равномерного движения гидравлическому уклону [см. (3-109) и (3-110)].
Формула (4-95) называется формулой Шези. Она имеет очень большое значение в практике. Коэффициент С (общепринятое обозначение), входящий в (4-95), называется коэффициентом Шези.
Сопоставляя (4-94) и (4-95), видим, что
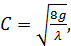 (4-96)
(4-96)
а следовательно,
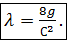 (4-97)
(4-97)
Формулы (4-96) и (4-97) связывают коэффициент гидравлического трения λ. и коэффициент Шези С. Как видно, зная λ, легко найти С. Поскольку λ является безразмерным коэффициентом, то коэффициент Шези, как видно из (4-96), имеет размерность. Размерность С равна корню квадратному из размерности ускорения.
Так как λ для квадратичной области сопротивлений зависит только от относительной шероховатости стенок русла и не зависит от числа Рейнольдса, а следовательно, и от рода жидкости, движущейся в русле, то в отношении С мы можем сказать то же самое: С зависит от относительной шероховатости стенок русла и не зависит от скорости движения v и вязкости жидкости, т. е. от коэффициента v (разумеется, если формулу Шези мы будем распространять и на область доквадратичного сопротивления, то в пределах этой области величина С окажется зависящей от Re).
В практике обычно величину С принято определять по специальным формулам (см. ниже § 4-13); вообще же говоря, значение С для случая круглых и прямоугольных труб можно находить и по формуле (4-96).
Надо учитывать, что формула Шези (4-95), строго говоря, может использоваться только для квадратичной области сопротивления в случае установившегося равномерного движения жидкости в руслах так называемого «правильного» поперечного сечения (см. выше).
2°. Зависимости, вытекающие из формулы Шези.Исходя из формулы (4-95), можно получить следующие практически важные расчетные зависимости:
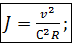 (4-98)
(4-98)
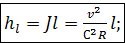 (4-99)
(4-99)
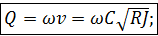 (4-100)
(4-100)
где l – длинна потока.
3°. Модуль расхода К. Введем обозначение
(I) 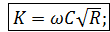 (4-101)
(4-101)
при этом формула (4-100) перепишется в виде
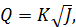 (4-102)
(4-102)
(II) 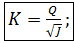 (4-103)
(4-103)
Как видно, модуль расхода К имеет два выражения: (I) и (II). Из (4-102) следует, что К представляет собой расход Q при J = 1,0. Из этой же формулы видно, что размерность величины К та же, что и расхода Q (поскольку J = hl: l — величина безразмерная).
Из формулы (4-103) получаем:
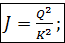 (4-104)
(4-104)
а следовательно,
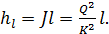 (4-105)
(4-105)
4°. Модуль скорости W. Введем обозначение
(I) 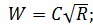 (4-106)
(4-106)
при этом формула (4-95) перепишется в виде
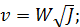 (4-107)
(4-107)
и, следовательно, для равномерного движения
(II) 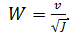 (4-108)
(4-108)
Как видно, модуль скорости W имеет два выражения: (I) и (II). Из (4-107) следует, что W представляет собой скорость v при J = 1,0. Размерность W та же, что и v.
Из (4-108) получаем:
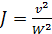 , (4-109)
, (4-109)
а следовательно,
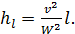 (4-110)
(4-110)
Понятиями модуля расхода К и модуля скорости W широко пользуются при практических расчетах труб и каналов.
5°. Эмпирические формулы для определения коэффициента Шези С.Решим уравнение Шези (4-95) в отношении С:
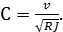 (4-111)
(4-111)
Наблюдая какой-либо водоток и замеряя в натуре величины v, R и J, можем по формуле (4-111)вычислить С для рассматриваемого водотока.
Многие исследователи проводили подобного рода измерения, и в результате было предложено много различных эмпирических формул для С. Эти формулы дают, конечно, разную величину С для данного конкретного случая. Такое положение объясняется приближенностью упомянутых эмпирических формул.
Таблица 4-3
Коэффициент шероховатости п для различных водотоков (для размеров в метрах и секундах)
| Материал стенок русла или описание водотока | Минимальный nmin | Нормальный n | Максимальный nмакс |
| А. Трубы и туннели | |||
| Стекло…………………………………………………………………. | 0,009 | 0,010 | 0,013 |
| Латунь…………………………………………………………………. | 0,009 | 0,010 | 0,013 |
| Сталь: | |||
| а) фланцевые и сварные соединения………….. | 0,010 | 0,012 | 0,014 |
| б) клепаные и резьбовые соединения…………. | 0,013 | 0,016 | 0,017 |
| Чугун: | |||
| а) с покрытием битумом…………………………….. | 0,010 | 0,013 | 0,014 |
| б) без покрытия битумом…………………………… | 0,011 | 0,015 | 0,016 |
| Деревянная клепка……………………………………………….. | 0,010 | 0,012 | 0,014 |
| Деревянная обработанная обшивка………………………. | 0,015 | 0,017 | 0,020 |
| Бетонная труба без засорения……………………………….. | 0,010 | 0,011 | 0,013 |
| Бетонная труба с некоторым засорением………………. | 0,011 | 0,013 | 0,014 |
| Бетонная труба с необработанной поверхностью, выполняемая в гладкой деревянной опалубке | 0,012 | 0,014 | 0,016 |
| То же в негладкой опалубке…………………………………. | 0,015 | 0,017 | 0,020 |
| Дренажная труба (из обожженной глины) | 0,011 | 0,013 | 0,017 |
| Канализационная труба, покрытая осадками сточных вод……………………………………………………………….. | 0.012 | 0,013 | 0.016 |
| Б. Облицовки безнапорных каналов | |||
| Асфальт……………………………………………………………….. | 0,013 | — | 0,016 |
| Сталь неокрашенная…………………………………………….. | 0.011 | 0,012 | 0,014 |
| Сталь окрашенная………………………………………………… | 0,012 | 0,013 | 0,017 |
| Дерево сгроганое…………………………………………………. | 0.010 | 0,012 | 0,014 |
| Цементный раствор……………………………………………… | 0,011 | 0,013 | 0,015 |
| Бетон затертый…………………………………………………….. | 0,011 | 0,013 | 0,015 |
| Торкрет………………………………………………………………… | 0,016 | 0,020 | 0,025 |
| Бетон по ровной скальной поверхности……………….. | 0,017 | 0,020 | — |
| Бетон по неровной скальной поверхности……………. | 0,022 | 0,027 | — |
| В. Безнапорные каналы без облицовки | |||
| В-1. Нескальный грунт | |||
| Чистый, только что выполненный……………………….. | 0,016 | 0,018 | 0,020 |
| Чистый, после выветривания……………………………….. | 0,018 | 0,022 | 0,025 |
| Чистый; ложе канала гравелистое………………………… | 0,022 | 0,025 | 0,030 |
| В канале небольшая растительность……………………… | 0,022 | 0,027 | 0,033 |
| Заросший травой………………………………………………….. | 0,025 | 0,030 | 0,033 |
| С густой травой и водорослями……………………………. | 0,030 | 0,035 | 0,040 |
| Откопанный драглайном или землечерпалкой (без растительности)…………………………………………………… | 0,025 | 0,028 | 0,033 |
| То же с растительностью………………………………………. | 0,035 | 0,050 | 0,060 |
| Не поддерживаемый в исправности (трава и кусты не расчищаются)………………………………………………….. | 0,050 | 0,100 | 0,140 |
| В-2. Скальный грунт | |||
| С гладкими стенками…………………………………………… | 0,025 | 0,035 | 0,040 |
| С неровными стенками………………………………………… | 0,035 | 0,040 | 0,050 |
| Г. Естественные водотоки | |||
| Г-1. Малые потоки (шириной менее 30 м) | |||
| Равнинные…………………………………………………………… | 0,025 | 0,070 | 0,150 |
| Горные………………………………………………………………… | 0,030 | 0,045 | 0,070 |
| Г-2. Русла с поймой | |||
| Пойма без кустарников и деревьев……………………….. | 0,025 | – | 0,050 |
| Пойма, покрытая кустарником…………………………….. | 0,035 | — | 0,160 |
| Пойма, покрытая деревьями…………………………………. | 0,110 | — | 0,200 |
| Г-3. Большие потоки | |||
| Правильные поперечные сечения русла; кустарников и валунов нет………………………………………………… | 0,025 | — | 0.060 |
Примечание. Значения п, обычно рекомендуемые для проектирования, набраны в таблице жирным шрифтом Эмпирические формулы для С, в которые входит и, были приведены в тексте книги для размеров в метрах и секундах.
Если, однако, отбросить устаревшие формулы для С и пользоваться более совершенными, то оказывается, что расхождение между величинами С, найденными по этим формулам для данного конкретного случая, не столь велико.
Приведем здесь только следующие формулы для С (размеры в метрах и секундах).
1. Так называемая сокращенная формула Гангилье — Куттера:
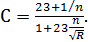 (4-112)
(4-112)
где n-коэффициент шероховатости стенок русла (имеющий размерность).
Гангилье и Куттер составили краткую таблицу численных значений n для стенок русла разной шероховатости. В табл. 4-3 приводим уточненные значения n, заимствованные из [4-9].
Таблици 4-4
Значения коэффициента С по формуле Маниинга 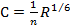 (метры и секунды)
(метры и секунды)
| R, м | п | ||||||||||
| | 0,011 | 0,013 | 0,014 | 0,017 | 0,020 | 0,025 | 0,030 | 0,035 | 0,040 | 0,045 | 0,050 |
| 0,30 | 74,4 | 63,0 | 58,4 | 48,1 | 40,9 | 32,7 | 27,3 | 23,4 | 20,4 | 18,2 | 16,4 |
| 0,32 | 75,2 | 63,6 | 59.1 | 48,6 | 41,4 | 33,1 | 27,5 | 23,6 | 20,7 | 18,4 | 16,5 |
| 0,34 | 76,0 | 64,3 | 59,7 | 49,1 | 41,8 | 33,4 | 27,8 | 23,9 | 20,9 | 18,6 | 16,7 |
| 0,36 | 76,7 | 64,9 | 60,3 | 49.6 | 42,2 | 33,7 | 28,1 | 24,1 | 21,1 | 18,7 | 16,9 |
| 0,38 | 77,4 | 65,5 | 60,8 | 50,1 | 42,6 | 34,0 | 28,4 | 24,3 | 21,3 | 18,9 | 17,0 |
| 0,40 | 78,1 | 66,0 | 61,3 | 50,5 | 42,9 | 34,3 | 28,6 | 24,5 | 21,4 | 19,1 | 17,2 |
| 0,42 | 78,7 | 66,6 | 61,8 | 50,9 | 43,3 | 34,6 | 28,9 | 24,7 | 21,6 | 19,2 | 17,3 |
| 0,44 | 79,3 | 67,1 | 62,3 | 51,3 | 43,6 | 34,9 | 29,1 | 24,9 | 21,8 | 19,4 | 17,4 |
| 0,46 | 79,9 | 67,6 | 62,8 | 51,7 | 43,9 | 35,2 | 29,3 | 25,1 | 22,0 | 19,5 | 17,6 |
| 0,48 | 80,4 | 68,1 | 63,2 | 52,0 | 44,2 | 35,4 | 29,5 | 25,3 | 22,1 | 19,7 | 17,7 |
| 0,50 | 81,0 | 68.5 | 63,6 | 52,4 | 44,5 | 35,6 | 29,7 | 25,5 | 22,3 | 19,8 | 17,8 |
| 0,55 | 82,3 | 69,6 | 64,6 | 53,3 | 45,3 | 36,2 | 30,2 | 25,9 | 22,6 | 20,1 | 18,1 |
| 0,60 | 83,5 | 70,6 | 65,6 | 54,0 | 45,9 | 36,7 | 30,6 | 26,2 | 23,0 | 20,4 | 18,4 |
| 0,65 | 84,6 | 71,6 | 66,5 | 54,7 | 46,5 | 37,2 | 31,0 | 26,6 | 23,3 | 20,7 | 18,6 |
| 0,70 | 85,7 | 72,5 | 67,3 | 55,4 | 47,1 | 37,7 | 31,4 | 26,9 | 23,6 | 20.9 | 18,8 |
| 0,75 | 86,7 | 73,3 | 68,1 | 56,1 | 47,7 | 38,1 | 31,8 | 27,2 | 23,8 | 21,2 | 19,1 |
| 0,80 | 87,6 | 74,1 | 68,8 | 56,8 | 48,2 | 38,5 | 32.1 | 27,5 | 24,1 | 21,4 | 19,3 |
| 0,85 | 88,5 | 74,9 | 69,5 | 57,2 | 48,7 | 38,9 | 32.4 | 27,8 | 24,3 | 21.6 | 19,5 |
| 0,90 | 89,3 | 75,6 | 70,2 | 57,8 | 49,1 | 39,3 | 32,8 | 28,1 | 24,6 | 21,8 | 19,7 |
| 0,95 | 90,1 | 76,3 | 70,8 | 58,3 | 49,6 | 39,7 | 33,0 | 28,3 | 24,8 | 22,0 | 19,8 |
| 1,00 | 90,9 | 77,0 | 71,4 | 58,8 | 50,0 | 40,0 | 33,3 | 28,6 | 25,0 | 22,2 | 19,9 |
| 1,10 | 92,4 | 78,2 | 72,6 | 59,8 | 50,8 | 40,6 | 33,9 | 29,0 | 25,4 | 22,6 | 20,3 |
| 1,20 | 93,7 | 79,3 | 73,6 | 60,6 | 51.5 | 41,2 | 34,4 | 29,5 | 25,8 | 22,9 | 20,6 |
| 1,30 | 95,0 | 80,4 | 74,6 | 61,5 | 52,2 | 41,8 | 34,8 | 29,8 | 26,1 | 23,2 | 20,9 |
| 1,40 | 96,2 | 81,4 | 75,6 | 62,2 | 52,9 | 42,3 | 35,3 | 30,2 | 26,4 | 23,5 | 21,2 |
| 1,50 | 97,3 | 82,3 | 76,4 | 62,9 | 53,5 | 42,8 | 35,7 | 30,6 | 26,8 | 23,8 | 21,4 |
| 1,60 | 98,3 | 83,2 | 77,2 | 63,6 | 54,1 | 43,3 | 36,1 | 30,9 | 27,0 | 24,0 | 21,6 |
| 1,70 | 99,3 | 84,1 | 78,0 | 64,3 | 54,6 | 43,7 | 36,4 | 31,2 | 27,3 | 24,3 | 21,9 |
| 1,80 | 100,3 | 84,8 | 78,8 | 64,9 | 55,1 | 44,1 | 36,8 | 31,5 | 27,6 | 24,5 | 22,1 |
| 1,90 | 101,2 | 85,6 | 79,5 | 65,5 | 55,6 | 44,5 | 37,1 | 31,8 | 27,8 | 24,7 | 22,3 |
| 2,00 | 102,0 | 86,3 | 80,2 | 66,0 | 56,1 | 44,9 | 37,4 | 32,1 | 28,1 | 24,9 | 22,5 |
| 2,20 | 103,7 | 87,7 | 81,5 | 67,1 | 57,0 | 45,6 | 38,0 | 32,6 | 28,5 | 25,3 | 22,8 |
| 2,40 | 105,2 | 89,0 | 82,7 | 68,1 | 57,8 | 46,3 | 38,6 | 33,1 | 28,9 | 25,7 | 23,2 |
| 2,60 | 106,6 | 90,2 | 83,8 | 69,0 | 58,6 | 46,9 | 39,1 | 33,5 | 29,3 | 26,1 | 23,5 |
| 2,80 | 108.0 | 91,3 | 84,8 | 69,8 | 59,4 | 47,5 | 39,6 | 33,9 | 29,7 | 26,4 | 23,7 |
| 3,00 | 109,2 | 92,4 | 85,8 | 70,6 | 60,0 | 48,0 | 40,0 | 34,3 | 30,0 | 26,7 | 24,0 |
| 3,50 | 112,0 | 94,8 | 88.0 | 72,5 | 61,6 | 49,3 | 41,1 | 35,2 | 30,8 | 27,4 | 24,6 |
| 4,00 | 114,5 | 97.0 | 90,0 | 74.1 | 63,0 | 50,4 | 42,0 | 36,0 | 31,5 | 28,0 | 25,2 |
| 4,50 | 116,8 | 98,8 | 91.8 | 75,6 | 64,2 | 51,4 | 42,8 | 36,7 | 32,1 | 28,6 | 25,7 |
| 5,00 | 118,9 | 100,6 | 93,4 | 76,9 | 65,4 | 52,3 | 43,6 | 37,4 | 32,7 | 29,1 | 26.1 |
2. Формула Маннинга:
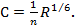 (4-113)
(4-113)
3. Формула Павловского, полученная для случая, когда R < (3,0 ÷ 5,0):
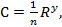 (4-114)
(4-114)
где
 (4-115)
(4-115)
причем для у дается относительно сложная эмпирическая формула (здесь не приводимая).
4. Формула[30] Бахметева и Федорова:
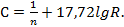 (4-116)
(4-116)
В формулы (4-113)— (4-116) входит коэффициент шероховатости, который назначается по шкале Гангилье и Куттера (табл. 4-3).
Практически вычислять С по этим формулам почти никогда не приходится, так как применительно к ним составлены соответствующие расчетные таблицы и графики. Например, применительно к формуле Павловского составлен график на рис. 4-26. Применительно к наиболее удобной формуле Маннинга — табл. 4-4. Установив по табл. 4-3 значение п, относящееся к данному конкретному случаю, и определив гидравлический радиус, мы по упомянутому графику или табл. 4-4 легко можем найти С. Надо подчеркнуть, что все приведенные эмпирические и полуэмпирические формулы для С (относящиеся к равномерному установившемуся движению жидкости) являются приближенными, причем значения и, входящие в них, приходится устанавливать по табл. 4-3 на основании чисто описательных (а не количественных) характеристик русла (так же как и значения Δ; см. выше). Поэтому при выборе для расчета той или другой из приведенных формул главным образом обращают внимание на простоту определения С по принятой формуле.[31] С этой точки зрения непосредственное применение в расчете формулы Павловского не может быть оправдано: эта формула, являясь весьма сложной, включает в себя, вместе с тем, весьма приближенный параметр п.
Как видно, в рассматриваемой области существует два разного вида оформления расчета: а) расчет с использованием величин Δ и λ и б) расчет с использованием коэффициента п. Заметим, что во всяком случае при расчете земляных каналов и естественных русел, должен использоваться второй вид расчета (с применением коэффициента п, в отношении которого мы имеем значительно более обширные экспериментальные данные, чем в отношении величины Δ).[32]
В литературе встречаются также формулы для С, относящиеся к области доквадратичного сопротивления. К числу таких формул принадлежит, например, так называемая полная формула Гангилье — Куттера; согласно этой формуле, которая имеет относительно сложный вид и рекомендуется ее авторами для применения в случае J < 0,005, величина С оказывается зависящей не только от R и п, но и от J.
А. Д. Альтшуль, используя некоторые полуэмпирические зависимости, предложил для открытых русел так называемую обобщенную формулу, действительную для квадратичной и для доквадратичной областей сопротивления, а также для области гладких русел:
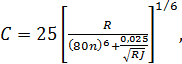 (4-117)
(4-117)
где R – в м; С – в м1/2/с
Эта зависимость при больших RJ (квадратичная область) оказывается аналогичной формуле Маннинга; при малых же RJ и малых значениях коэффициента п (гладкие русла) она дает результаты, близкие к тем, которые получаются по так называемой формуле Блазиуса. Значения коэффициента п, входящего в (4-117), можно брать из табл. 4-3.

§
В § 3-16 нами было пояснено особое очень существенное физическое явление — явление передачи механической энергии от одной элементарной струйки к другой через боковую разграничивающую их поверхность. При этом было обращено внимание на то, что такая передача энергии может осуществляться, например, при ламинарном движении жидкости, когда турбулентный обмен жидкости между соседними струйками отсутствует.
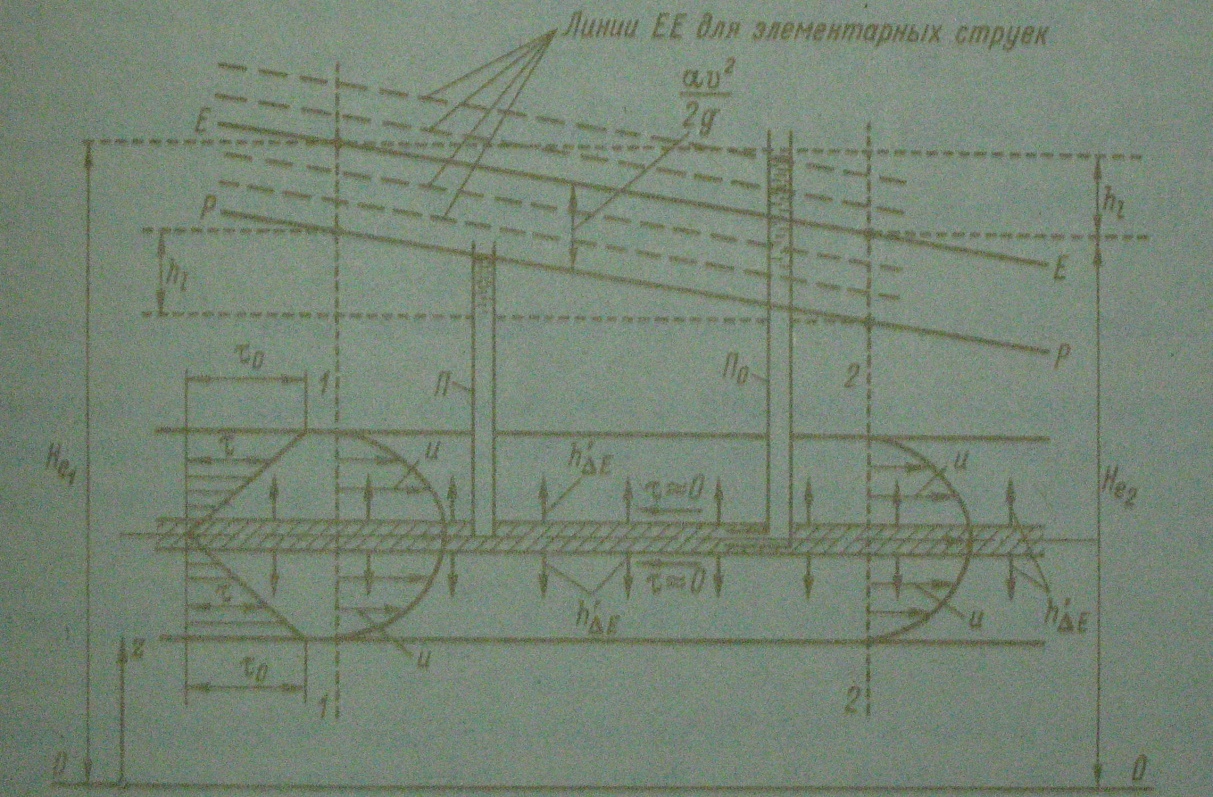
Рис. 4-27. «Диффузия» механической энергии (в размере 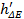 через боковую поверхность элементарных струек (плоская задача) П — пьезометр; П0 — трубка Пито;
через боковую поверхность элементарных струек (плоская задача) П — пьезометр; П0 — трубка Пито;
– – – – – линии ЕЕ для элементарных струек
Величина «диффузионного изменения напора» («диффузионного изменения удельной энергии» вдоль струйки) была обозначена нами через 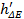 .
.
Наличие описанного в § 3-16 «поперечного потока механической энергии» может быть строго обосновано для ламинарного движения при помощи так называемой «функции диссипации механической энергии» Ф (хорошо известной из математической механики жидкости). Для простейшего случая (плоская задача, равномерное ламинарное движение; рис. 4-27) эта функция имеет вид[33]
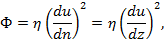
где Ф – работа (в единицу времени — в секунду), выполненная продольными силами трения Т (см. рис. 4-5) внутри одной кубической единицы неподвижного пространства, имеющей небольшую высоту dz = dn, при которой величина du/dn = du/dz может считаться постоянной:
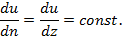
Очевидно, разбивая весь отсек жидкости (рис. 4-27), заключенный между расчетными сечениями 1 — 1 ч 2 — 2 насоответствующие кубические единицы и затем подсчитывая для всех этих кубических единиц значения Ф, мы можем найти и работу сил трения (в секунду), т. е. ∑Ф в пределах потока, ограниченного сечениями 1 — 1 и 2 — 2. Легко видеть, что потеря напора от сечения 1 — 1 до сечения 2 — 2 может быть представлена формулой:
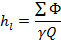
которая вполне согласуется с соответствующей формулой Пуазейля.
Из рис. 4-27 видно распределение величины 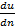 (или
(или 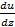 ) по живому сечению потока. Имея в виду такое распределение величин
) по живому сечению потока. Имея в виду такое распределение величин 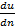 , а также учитывая приведенное выше выражение для Ф, можно утверждать следующее:
, а также учитывая приведенное выше выражение для Ф, можно утверждать следующее:
а) внутри центральной струйки, для которой du/dn ≈ 0 работа сил трения будет близка к нулю; поэтому данная центральная струйка почти не будет нагреваться;
б) пристенная же струйка, для которой 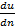 велико, будет нагреваться значительно.
велико, будет нагреваться значительно.
Выше мы имели в виду ламинарный режим. В случае турбулентного режима при вычислении Ф в формулу подставляют обычно вместо η величину ηт (см. § 4-7).
В заключение отметим следующее. Данный вопрос (о передаче механической энергии через боковую поверхность струек) может приобретать существенное практическое значение в том случае, когда при выполнении гидравлических расчетов приходится расчленять «целый поток» на отдельные фрагменты теми или другими продольными (по отношению к потоку) поверхностями; здесь, естественно, может возникнуть потребность количественно учесть соответствующую величину 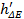 . Кроме того, данный вопрос представляет еще интерес в том отношении, что, рассматривая его, можно дополнительно объяснять с физической (энергетической) точки зрения возникновение и существование в потоке водоворотных областей (характеризуемых «возвратным течением»; см. § 4-14).
. Кроме того, данный вопрос представляет еще интерес в том отношении, что, рассматривая его, можно дополнительно объяснять с физической (энергетической) точки зрения возникновение и существование в потоке водоворотных областей (характеризуемых «возвратным течением»; см. § 4-14).
§
1°. Два вида явления отрыва транзитной струи от стенок русла. При
обтекании турбулентным потоком какой-либо преграды (рис. 4-28, а) происходит отрыв транзитной струи от стенки русла. При этом получаем области А, заполненные множеством водоворотов; такое водоворотное движение в этих областях носит резко выраженный неустановившийся характер. Будем именовать: области А водоворотными (или, иначе, вальцовыми или циркуляционными) областями;[34] остальную часть потока — транзитной струей; поверхность abcd, отделяющую транзитную струю от водоворотных зон,— поверхностью раздела.
Поверхность раздела бывает выражена нерезко; она носит неустановившийся и неустойчивый характер: периодически эта поверхность получает местные искривления, которые прогрессируют и переходят в отдельные водовороты (вальцы); эти водовороты попадают затем в транзитную струю и уносятся ею; поверхность же раздела снова восстанавливается с тем, чтобы в последующие моменты времени опять распасться и свернуться в водовороты, и т. д Постоянное возникновение в районе поверхности раздела водоворотов, попадающих в транзитную струю, способствует повышению пульсации скоростей и давлений в ней.
Переходя от рис. 4-28,а к осредненному потоку, водоворотные области показывают несколько условно — в виде, изображенном на рис. 4-28,б; штриховыми линиями здесь представлены линии тока осредненного потока, а не траектории частиц жидкости.
Именно в таком виде и будем изображать водоворотные области. Предполагается, что линия тока abсd на рис. 4-28, б намечена так, что: а) в любой ее точке осредненная (во времени) величина проекции актуальной скорости на нормаль к линии abсd равна нулю; б) величина расхода вдоль транзитной струи, выражаемая площадью соответствующей части эпюры скоростей, является постоянной. Строго говоря, такие условия могут быть удовлетворены только приближенно (если живые сечения считать плоскими).
Водоворотные области характеризуются возвратным течением. Эпюры осредненных скоростей дают нулевые значения продольных скоростей и не только на стенках русла, но и на «средней» линии водоворотной области (см. чертеж).
Сечение 2 — 2, где заканчивается вторая водоворотная зона, характеризуется как повышенной пульсацией скоростей и давлений, так и наличием сильно деформированной эпюры осредненных скоростей. На протяжении некоторого участка потока между сечениями 2 — 2 и 3—3 происходит: а) затухание пульсаций до величин, свойственных равномерному движению, и б) выравнивание эпюры скоростей, причем в сечении 3 — 3 эта эпюра принимает «нормальную» форму, свойственную равномерному течению.
Как видно, водоворотные области, расположенные между сечениями 1—1 и 2 — 2 (рис. 4-28, б), нарушают «нормальный» характер движения жидкости на некоторой длине lперех от сечения 2 — 2 до сечения 3 — 3; этот участок назовем переходным или послеводоворотным.[35]
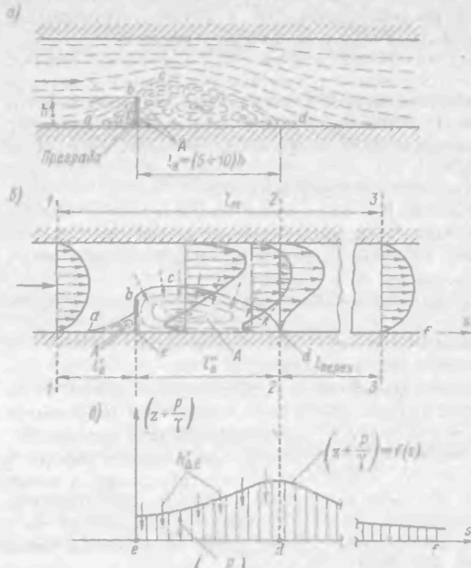
Рис. 4-28. Обтекание преграды турбулентным потоком:
а – действительный поток, б – осредненный поток (неполная воображаемая модель Рейнольдса — Буссинеска); поперечными стрелками показан поток энергии, поступающий в водоворотную зону со стороны транзитной струи; в — схема изменения величины (z р/γ) вдоль стенки ef (у которой всюду u= 0)
Через поверхность раздела благодаря пульсационным поперечным скоростям происходит некоторый обмен жидкости между водоворотной областью и транзитной струей. Турбулентные касательные напряжения (см. § 4-7), действующие вдоль поверхности раздела, относительно велики. Поэтому потеря напора в пределах водоворотной зоны получается большая. На длине пе-реходного (послеводоворотного) участка имеем также повышенные потери напора сравнительно с дальнейшими участками равномерного движения.
Если по поверхности раздела bcd установить криволинейную твердую стенку русла, то получим безотрывную транзитную струю; потеря напора при этом значительно уменьшится. Такое снижение потерь напора объясняется тем, что касательные напряжения, возникающие вдоль установленной стенки, значительно меньше турбулентных касательных напряжений, действующих вдоль поверхности раздела.
Поясненный выше отрыв транзитной струи может быть назван (несколько условно) «инерционным отрывом транзитной струи от стенки русла». Помимо такого отрыва струи, можно различать еще «отрыв транзитной струи (а в соответствующих случаях и отрыв пограничного слоя), обусловленный диффузией механической энергии поперек потока». Примером отрыва струи, вызванного поперечной диффузией механической энергии, может являться поток в сильно расширяющемся насадке (см. рис. 4-30), а также случай так называемого гидравлического прыжка.[36] Такого рода отрывы, по нашему мнению, обусловливаются тем, что хотя полная удельная механическая энергия жидкости «целого потока» снижается по течению (за счет потерь напора), вместе с тем за счет поперечной диффузии энергии (направленной в сторону стенки русла; см. § 3-16) энергия, принадлежащая пристенной (придонной) элементарной струйке, начинает при определенных условиях увеличиваться по направлению общего (главного) течения жидкости (см. рис. 4-30,г).[37]
Такое положение, очевидно, позволяет объяснять более полно возможность возвратного течения тяжелой реальной жидкости в районе водоворотных областей, вызванных и «инерционным отрывом».
2°. Общий характер местных потерь напора. На отдельных участках русла (трубопровода), где имеются повороты, местные расширения и сужения русла и т. п., возникают местные потери напора, обусловленные, так же как и потери по длине, работой сил трения. Но эти силы трения в узлах резко изменяющегося движения, свойственных «местным сопротивлениям», распределяются в потоке весьма неравномерно.
Такие места потока в общем случае характеризуются:
а) местными искривлениями линий тока и живых сечений;
б) уменьшением или увеличением живых сечений вдоль потока;
в) возникновением местных отрывов транзитной струи от стенок русла,
а следовательно, появлением водоворотных областей.
В пределах такого рода узлов, а также в пределах некоторого расстояния за ними наблюдаем:
1) деформацию эпюр осредненных скоростей вдоль потока;
2) повышение пульсации скоростей и давлений.
Как было указано, повышение пульсации скоростей обусловливает увели-чение касательных турбулентных напряжений (в рассматриваемом осредненном потоке), что, в свою очередь, влечет за собой повышение потерь напора.
Таковы условия возникновения так называемых местных потерь напора hj.
Рассматривая далее вопрос о величине местных потерь напора в случае турбулентного движения, будем иметь в виду только область квадратичного сопротивления.
В заключение подчеркнем, что местная потеря напора hj в рассматриваемом выше частном случае (см. рис. 4-28) возникает на длине
Напомним, (см. § 4-1), что длина lм в практике часто бывает пренебрежимо малой сравнительно с общей длиной потока (трубопровода). Именно поэтому, как было выше отмечено, считают при выполнении обычных расчетов, что lм = 0, причем найденное значение местной потери напора hj относят к одному поперечному сечению потока; потерю же по длине hl условно считают распределенной по всей длине рассчитываемого потока равномерно.
§ 4-15. ПОТЕРИ НАПOPA ПРИ РЕЗКОМ РАСШИРЕНИИ НАПОРНОГО ТРУБОПРОВОДА (ФОРМУЛА БОРДА). ВЫХОД ИЗ ТУРБУЛЕНТНОГО БАССЕЙНА.
На рис. 4-29, а показан случай, когда труба, имеющая диаметр D1 переходит в трубу, имеющую больший диаметр D2 (D2 > D1). Струя, выходящая из первой трубы, на некоторой длине lВ (в связи с наличием продольных сил трения, действующих на боковой ее поверхности) расширяется и в сечении 2′ — 2′ заполняет все сечение второй трубы. На длине lВ струи имеет место отрыв ее от стенок трубы и образование описанной выше водоворотной зоны А, имеющей в данном случае кольцевую форму. Струя в пределах между сечениями 1 — 1 и 2′ — 2′ может иметь несимметричный вид (получается искривление оси потока).[38]
На протяжении расширяющейся струи (между сечениями 1—1 и 2′ — 2′) и переходного участка (между сечениями 2′ — 2′ и 2—2) получаем неравномерное движение, местами резко изменяющееся.
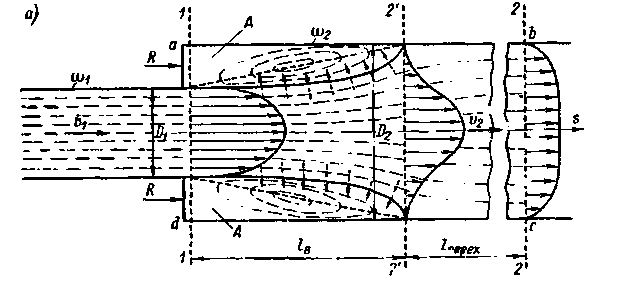
Рис. 4-29. Резкое расширение потока: а — к выводу формулы Борда; модель Рейнольдса—Буссинеска (поперечными стрелками показан поток энергии, передающийся от транзитной струи в водоворотную область); б — потери напора «на выход»; в — случай идеальной жидкости (А — цилиндрическая струя; Б — область покоящейся жидкости)
Между сечениями 1—1 и 2—2 возникает местная потеря напора hj Эту потерю назовем потерей напора на резкое расширение (р. р) потока и далее будем обозначать ее через (hj)p р или просто через hp. р. Впервые расчетную зависимость для hp p получил французский инженер Борда, который уподобил резкое расширение струи явлению удара неупругих твердых тел. Заметим, что в связи с этим потерю hp p иногда называют потерей на удар (что в настоящее время не следует делать).
Выведем формулу Борда, пользуясь гидравлическим уравнением кинетической энергии (уравнением Бернулли) и гидравлическим уравнением количества движения (рассматривая эти два уравнения как систему уравнений). Напомним, что уравнение Бернулли (полученное нами, исходя из теоремы, касающейся изменения кинетической энергии; см. начало § 3-12) учитывает как внешние, так и внутренние силы; гидравлическое же уравнение количества движения (см. § 3-22) учитывает только внешние силы. Решая совместно два эти уравнения, получаем возможность выделить работу внутренних сил трения, обусловливающих искомую потерю напора.
Имея в виду сказанное, соединяем сечения 1 — 1 и 2—2 уравнением Бернулли. В результате получаем
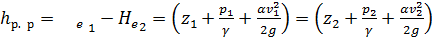 (4-118)
(4-118)
Индексы 1 и 2 указывают, что соответствующие величины относятся или к сечению 1-1, или 2-2, где сечение 1-1 совпадает с линией 1-1.
Для упрощения рассуждений будем рассматривать только горизонтальную трубу.[39] В районе сечений 1 —1 и 2 — 2 имеем равномерное движение и потому корректив кинетической энергии а для этих сечений будем считать равным единице. При этом (4-118) перепишем в виде
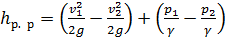 (4-119)
(4-119)
Разность давлений (p1 — p2) найдем, пользуясь гидравлическим уравнением количества движения (3-124), которое приложим к отсеку жидкости abcd,соединив этим уравнением сечения 1 — 1 и 2 — 2:
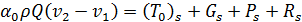 (4-120)
(4-120)
где 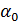 — корректив количества движения, который для сечений 1 — 1 и 2 — 2 можно принять также равным единице; (T0)s — проекция на направление движения внешней силы трения Т0, действующей со стороны стенок трубы на рассматриваемый отсек жидкости abcd. Так как длина участка потока между сечениями 1 — 1 и 2 — 2 невелика, то силой Т0 пренебрегаем и считаем (To)s = 0 (1-е допущение); Gs — проекция собственного веса отсека abcd на направление движения, Gs = 0; Рs, — сумма проекций на ось s сил гидродинамического давления Р1 и Р2, действующих соответственно на торцовые сечения 1 — 1 и 2 — 2 выделенного отсека транзитной струи (со стороны жидкости, находящейся слева и справа от этого отсека); Rs — проекция (на направление движения) реакции стенок (без учета сил трения); величина Rs = R, где сила R — давление вертикальной стенки ad, имеющей кольцевую форму, на жидкость (см. чертеж).
— корректив количества движения, который для сечений 1 — 1 и 2 — 2 можно принять также равным единице; (T0)s — проекция на направление движения внешней силы трения Т0, действующей со стороны стенок трубы на рассматриваемый отсек жидкости abcd. Так как длина участка потока между сечениями 1 — 1 и 2 — 2 невелика, то силой Т0 пренебрегаем и считаем (To)s = 0 (1-е допущение); Gs — проекция собственного веса отсека abcd на направление движения, Gs = 0; Рs, — сумма проекций на ось s сил гидродинамического давления Р1 и Р2, действующих соответственно на торцовые сечения 1 — 1 и 2 — 2 выделенного отсека транзитной струи (со стороны жидкости, находящейся слева и справа от этого отсека); Rs — проекция (на направление движения) реакции стенок (без учета сил трения); величина Rs = R, где сила R — давление вертикальной стенки ad, имеющей кольцевую форму, на жидкость (см. чертеж).
Величину (Рs, Rs) можно представить в виде
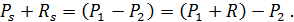 (4-121)
(4-121)
Давление в сечении 2—2 распределяется по гидростатическому закону, поскольку здесь имеем равномерное движение. Примем, что давление по всему сечению 1 — 1 (по площади ad, охватывающей транзитную струю и водоворотную область) распределяется также по гидростатическому закону (2-е допущение). При этом можем написать:
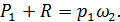 (4-122)
(4-122)
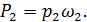 (4-123)
(4-123)
где р1 и р2 — гидродинамические давления в центрах тяжести сечений 1 — 1 (круга ad) и 2 — 2 (круга be); ω2 — площадь сечения второй трубы (т. е. площадь круга ad или be). Подставляя (4-122) и (4-123) в (4-121), находим:
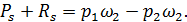 (4-124)
(4-124)
Учитывая (4-124), уравнение (4-120) переписываем в виде
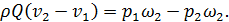 (4-125)
(4-125)
откуда имея в виду, что
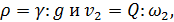 (4-126)
(4-126)
получаем
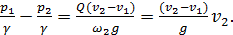 (4-127)
(4-127)
Подставляя (4-127) в (4-119), имеем
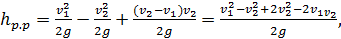 (4-128)
(4-128)
или окончательно
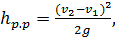 (4-129)
(4-129)
где разность (v1 — v2) называют потерянной скоростью.
Формула (4-129) называется формулой Борда. Согласно этой формуле
потеря напора при резком расширении равняется скоростному напору, отвечающему потерянной скорости.[40]
1) Преобразование формулы Борда:
а) Приведем выражение (4-129) к другому виду. Вынесем за скобки v1 тогда получим:
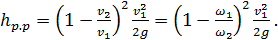 (4-130)
(4-130)
Обозначая
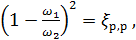 (4-131)
(4-131)
имеем
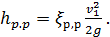 (4-132)
(4-132)
б) Вынося за скобки v2, получаем аналогично
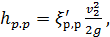 (4-133)
(4-133)
где
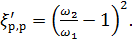 (4-134)
(4-134)
Коэффициенты 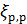 и
и 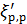 называются коэффициентами сопротивления при резком расширении потока.
называются коэффициентами сопротивления при резком расширении потока.
2) Местная потеря напора, получающаяся при выходе потока из трубы в бассейн больших размеров. Эту потерю называют потерей «на выход» (рис. 4-29,6), ее обозначают через hвых.
Данный случай является частным случаем предыдущего, когда ω2 значительно больше ω1 (ω2>> ω1). Имея это в виду, можем написать в соответствии с формулой (4-131), что
 (4-135)
(4-135)
а следовательно, потеря на выход будет
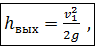 (4-136)
(4-136)
или, несколько точнее
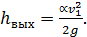 (4-137)
(4-137)
Если ω2 нельзя считать достаточно большой величиной, то hвыхможно представить зависимостью:
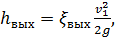 (4-138)
(4-138)
где
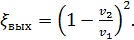 (4-138)
(4-138)
В заключение отметим следующее.
1) Соединяя уравнением Бернулли и уравнением количества движения сечения 2′ — 2′ и 2 — 2, мы можем получить приближенную формулу для потерь напора на длине переходного участка, а затем и на длине «водоворотного участка» [4-11, с. 153].
2) Возникает вопрос о возможности распространения формулы Борда на случай ламинарного движения жидкости. Здесь надо сказать следующее. Если 2-е допущение (о гидростатическом распределении давления по сечению 1-1; см. рис. 4-29,а) приемлемо для турбулентного движения, то для ламинарного движения, когда водоворотная зона А может отсутствовать, указанное допущение без соответствующих коррективов является, как правило, неприемлемым.
3) Надо учитывать, что в случае идеальной (невязкой) жидкости, когда касательные напряжения τ вовсе отсутствуют, мы, естественно, не можем представить себе поток, показанный на рис. 4-29, а. При отсутствии τ продольные скорости и должны распределяться равномерно по живым сечениям (рис. 4-29, в). При этом жидкость во второй трубе (см. область Б), окружающая цилиндрическую струю А, должна находиться в покое.
Струю идеальной жидкости можно представить себе расширяющейся только при особых условиях (начальных и граничных).
§4-16. ПОСТЕПЕННОЕ РАСШИРЕНИЕ ТРУБОПРОВОДА
(ДИФФУЗОР)
Диффузор (рис. 4-30) устраивают для уменьшения потери напора hp.p, возникающей при переходе трубы меньшего диаметра в трубу большего диаметра. Как показывает опыт, картина протекания жидкости в диффузоре имеет вид:
Рис. 4-30. Диффузоры (потоки представлены моделью Рейнольдса-Буссинеска); а) безотрывное движение; б) небольшой водоворот; в) сильно развитый водоворот; г) случай плоской задачи:
s0 – координата, направленная по стенке трубы; abcdea – эпюры напора Н’е; напор Не = (Ωэ): (Ω0),где Ω0– площадь эпюры скоростей (выражающая расход Q); Ωэ – площадь эпюры величины (H′edQ) [согласно формуле 3-95)]: а’ – e’ – неплоское живое сечение; lперех – длина переходного участка
а) при угле β в пределах
0 < β < 8 ÷ 10°
на всем протяжении диффузора наблюдается безотрывное протекание жидкости (рис. 4-30, а);
б) при
8 ÷ 10° < β < 50 ÷ 60°
получается отрыв струи от стенок (рис. 4-30,6), причем с увеличением угла β точка начала отрыва перемешается вверх по течению;
в) при
β > 50 ÷ 60°
на всем протяжении диффузора имеем отрыв транзитной струи от стенок (рис. 4-30, в)[41]
Потерю напора в диффузоре hдифф выражают в долях потери напора hp р, вычисленной по формуле (4-129):
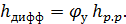 (4-140)
(4-140)
где 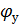 – эмпирический коэффициент.
– эмпирический коэффициент.
Величина φу в основном зависит от угла р. Как видно из графика (рис. 4-31), построенного на основании опытных данных, наивыгоднейший угол β, при котором получаются наименьшие потерн напора, будет β ≈ 6°.
В заключение отметим, что на рис. 4-30, г представлена схема (в виде модели Рейнольдса — Буссинеска), объясняющая (более подробно, чем то было сказано ранее) физические причины отрыва транзитной струи от стенки русла.
На этой схеме для, плоских живых сечений 1-1 и 2 – 2 изображены эпюры напоров Н’е (для элементарных струек):
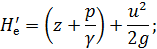
см. площади Qa1b1c1d1e1a1 и Qa2b2c2d2e2a2.
Площадь таких эпюр не выражает механическую энергию, проносимую жидкостью через живые сечения 1 – 1 и 2 – 2. Рассматривая для примера сечение 2 – 2, можем сказать, в соответствии с формулой (3-95), что энергию, проносимую через это сечение, выражает (для плоской задачи) площадь эпюры (Ωэ)2, каждая горизонтальная ордината которой равна H’edQ. Легко видеть, что полный напор в сечении 2—2 равен:
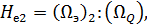
де  – площадь эпюры скоростей, дающая нам (для плоской задачи) величину расхода Q (который вдоль потока постоянен: Q = const).
– площадь эпюры скоростей, дающая нам (для плоской задачи) величину расхода Q (который вдоль потока постоянен: Q = const).
Площадь эпюры (  ), в связи с потерями напора, должна уменьшаться по течению также как и величина Не.
), в связи с потерями напора, должна уменьшаться по течению также как и величина Не.
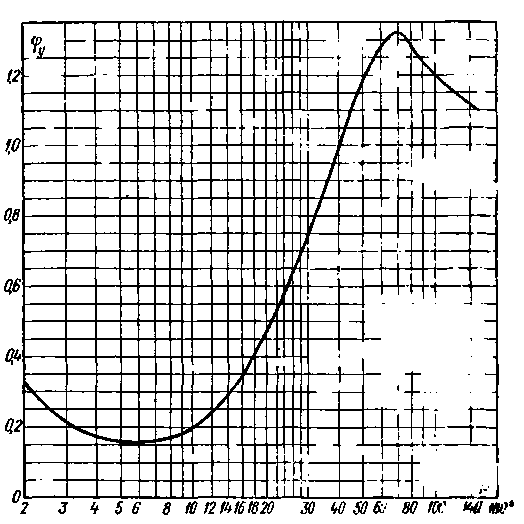
Рис. 4-31. График для определения коэффициента φу, входящего в формулу (4-140)
Вместе с тем, в связи с поперечной диффузией энергии полный напор у стенки трубы (где и ≈ 0) 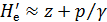 [см. на рис. 4-30, г схему графика
[см. на рис. 4-30, г схему графика
(z р/γ) = f (s0)] может увеличиваться вдоль общего направления течения; такое положение, как мы отмечали ранее, и может обусловливать «возвратное» течение жидкости, а следовательно, и отрыв транзитной струи от стенки. В связи с отрывом струи возникает водоворотная зона, существование которой обеспечивается поперечной (по отношению к потоку жидкости) диффузией механической энергии.[42]
§
На рис. 4-32 показаны различные случаи сужения трубопровода. Если предположить, что сечение «первой» трубы весьма велико, то вместо сужения трубопровода на рис. 4-32 получаем схемы входа потока из бассейна больших размеров в трубу.
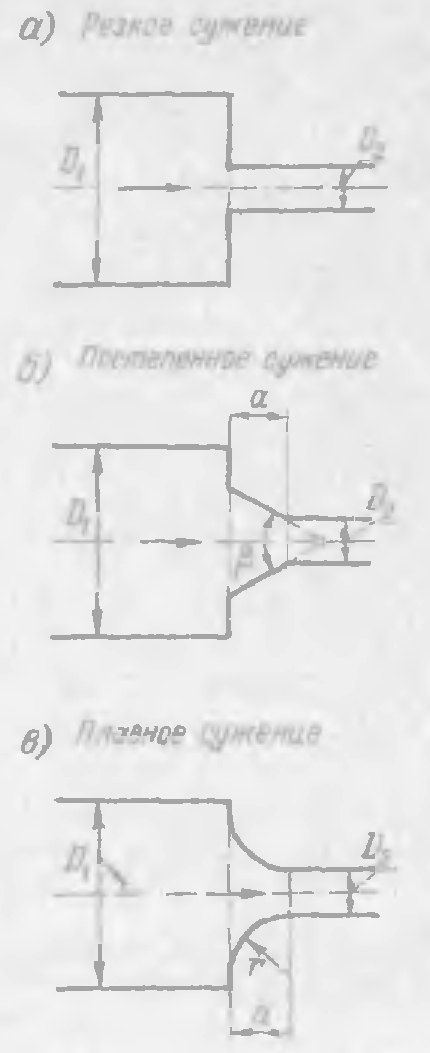
Рис. 4-32. График для определения коэффициента φу, входящего в формулу (4-140)
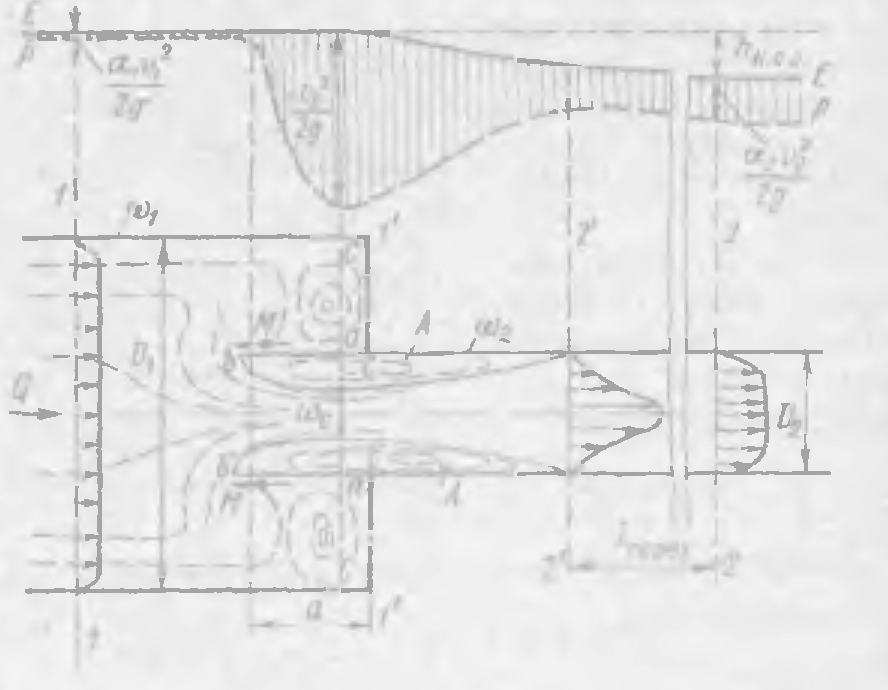
Рис. 4-33. Наиболее резкое сужение трубопровода
На рис. 4-33 представлен особый случай сужения, который может быть назван наиболее резким сужением. Если размер а (см. чертеж) удовлетворяет условию а > 0,5D2, то этот случай в отличие от остальных может быть решен (с некоторым все же приближением) теоретически примерно так же, как резкое расширение трубы (см. § 4-15).
Рассмотрим случай наиболее резкого сужения. Условия протекания жидкости здесь характеризуются следующим (рис. 4-33):
1) частицы жидкости М, движущиеся вдоль стенки ab, должны в точках b резко изменить направление своего движения на противоположное. При этом благодаря силам инерции частиц струя оторвется от стенки bс и мы получим кольцевую водоворотную область А.
2) в пределах водоворотной области А можно различать два участка транзитной струи: сужающийся, расположенный перед «сжатым сечением» С— С, и расширяющийся, расположенный за сжатым сечением С — С.
Как показывают опыты, потеря напора на сужающейся части струи (до сечения С — С) для турбулентного потока относительно мала в связи с тем, что пульсация скоростей на протяжении сужающихся потоков всегда снижается; кроме того, и длина сужающейся части струи невелика — равна примерно 0,5 D2.
В основном местная потеря напора сосредоточивается в пределах расширяющейся части струи (между сечениями С — С и 2′ — 2′).
Имея в виду такое положение, потерю напора для наиболее резкого сужения трубопровода (рис. 4-33) можем найти по формуле Борда, подставив в (4-129) вместо скорости v1 скорость vcв сжатом сечении С — С:
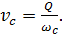 (4-141)
(4-141)
где ωс — площадь живого сечения транзитной струи в сжатом сечении
С — С:
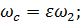 (4-142)
(4-142)
здесь 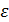 называется коэффициент сжатия струи
называется коэффициент сжатия струи
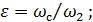 (4-143)
(4-143)
Используя указанные зависимости, получаем величину потерь напора для наиболее резкого сужения (н. р. с.)
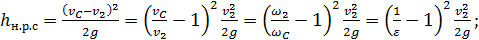 (4-144)
(4-144)
или
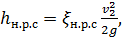 (4-145)
(4-145)
где коэффициент сопротивления наиболее резкого сужения потока
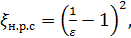 (4-146)
(4-146)
Как видно, с уменьшением е, т. е с увеличением сжатия струи в сечении С—С, коэффициент сопротивления должен увеличиваться и, следовательно, должны увеличиваться потери напора. Если пренебречь потерями напора до сжатого сечения С — С, как мы делали выше, то следует считать, что полученные формулы (4-145) и (4-146) относятся, собственно, к любой схеме,изображенной на рис. 4-32. Различие между этими схемами будет заключаться только в разных численных значениях коэффициента ε, входящего в формулу (4-146).
Условимся обозначать далее коэффициент сжатия для «наиболее резкого 1 сжатия» (рис. 4-33) через 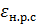 . Величина этого коэффициента, согласно И. Е. Идельчику, оказывается[43]
. Величина этого коэффициента, согласно И. Е. Идельчику, оказывается[43]
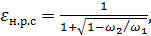 (4-147)
(4-147)
Подставляя (4-147) в (4-148), получаем
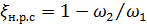 (4-146)
(4-146)
Рассмотренное наиболее резкое сужение, характеризуемое соотношениями (4-147) и (4-148), является наиболее неблагоприятным: для него имеем самую большую местную потерю. Остальные случаи характеризуются меньшим сжатием струи в сечении С — С, а следовательно, и меньшими потерями напора
В общем случае (рис. 4-32) местную потерю напора hcдля сужающегося трубопровода определяют по формуле:
 (4-149)
(4-149)
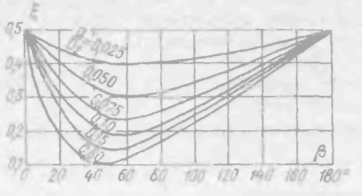
Рис. 4-34. График для определения «коэффициента ξ смягчения сужения», представленного на рис. 4-32, б
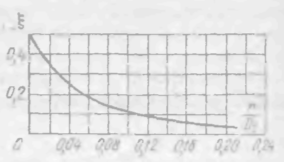
Рис. 4-35. График для определения «коэффициента ξ смягчения сужения», представленного на рис. 4-32, в
где коэффициент сопротивления сужения ξ с трубопровода считают равным:
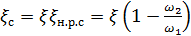 , (4-150)
, (4-150)
причем здесь ξ называют коэффициентом смягчения сужения.
Величину ξможно определить, пользуясь следующими эмпирическими данными.
1. Случай резкого сужения (р. с) трубопровода (рис. 4-32, a)
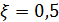 ,
,
а следовательно, коэффициент сопротивления, входящий в формулу (4-149) и обозначаемый здесь через ξ р.с., оказывается
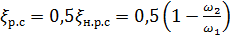 . (4-151)
. (4-151)
2. Случай постепенного сужения трубопровода (рис. 4-32,б). Здесь величина ξ находится в зависимости от угла β и отношения a/D2 (см. чертеж) по графику на рис. 4-34. Как видно из этого графика, минимальная потеря напора на вход получается при β = 40 ÷ 60°.
3. Случай плавного сужения трубопровода (рис. 4-32,в). Здесь величину β
находим в зависимости от r/D2 (где r — радиус скругления боковых стенок входа) по графику на рис. 4-35. Коэффициент ξ достигает минимума (ξ = 0,03) при r/D2 = 0,2 и далее остается постоянным.
Экспериментальные графики на рис. 4-34 и 4-35, заимствованные из [4-5], даются здесь для случая круглоцилиндрических труб. Однако этими графиками можно пользоваться и при расчете прямоугольных труб; но тогда при определении по графикам коэффициента ξ, входящего в формулу (4-150), под величиной D2 следует понимать гидравлический диаметр соответствующего водовода (Dr)2 [см. зависимость (4-83)].
Рассмотрим в заключение случай входа в трубопровод из весьма большого бассейна. Для этого случая, полагая в формуле (4-150) площадь ω = ∞, получаем
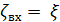 . (4-152)
. (4-152)
где 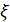 , — можем найти, как указано выше.
, — можем найти, как указано выше.
Зная  вх, потерю напора на вход hвх определяем по формуле (4-149), заменив в ней обозначения hc и
вх, потерю напора на вход hвх определяем по формуле (4-149), заменив в ней обозначения hc и  с обозначениями hвх и
с обозначениями hвх и  вх. Подчеркнем, что величина
вх. Подчеркнем, что величина  вх для случая входа в трубопровод, конструктивно оформленного в соответствии с рис. 4-32, а (т. е. для случая «резкое сужение») получается равной [при ω1 = ∞; см. формулу (4-151)]
вх для случая входа в трубопровод, конструктивно оформленного в соответствии с рис. 4-32, а (т. е. для случая «резкое сужение») получается равной [при ω1 = ∞; см. формулу (4-151)]
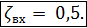 (4-153)
(4-153)
§
На рис. 4-36 для примера показаны два случая местных потерь напора (местных сопротивлений): задвижка и поворот трубы. Эти случаи и им подобные, так же как и сужения трубы (см. § 4-17), характеризуются наличием струи и водоворотных областей А. Как было указано выше, потеря напора hjглавным образом сосредоточивается только на участке струи за сжатым сечением, где имеется расширение струи. Поэтому hjв любом случае можно было бы определить в соответствии с формулой Борда, переписав ее так:
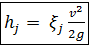 (4-154)
(4-154)
где 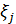 можно назвать коэффициентом местного сопротивления.
можно назвать коэффициентом местного сопротивления.
Рис. 4-34. Протекание жидкости при наличии задвижки З(а) и при наличии поворота трубы (б)
Согласно (4-134),
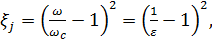 (4-155)
(4-155)
причем здесь со — живое сечение транзитной струи, заполняющей всю трубу; ωс – живое сечение транзитной струи по линий сжатого сечения С — С.
Однако практически ζj по (4-155) в общем случае найти затруднительно, так как нам неизвестна площадь ωс.
Учитывая вместе с тем приведенные соображения, Вейсбах предложил вычислять любую местную потерю напора по формуле (4-154), считая, что коэффициент местного сопротивления, входящий в эту формулу, в общем случае должен определяться экспериментальным путем для различных встречающихся в практике местных сопротивлений.
Экспериментальные значения ζj приводятся в справочной литературе. Некоторые сокращенные данные по этому вопросу даются ниже (стр. 194-203).
Величина ζjзависит от того, какую скорость будем подставлять в формулу Вейсбаха (4-154): относящуюся к сечению, взятому до местного сопротивления, или за ним. Из формулы (4-154) ясно, что величина hj прямо пропорциональна скоростному напору.
Практически во всех случаях hjопределяется по формуле (4-154), в которой ζj — эмпирический коэффициент пропорциональности; только в двух случаях (при резком расширении и наиболее резком сужении) этот коэффициент устанавливается теоретическим путем — путем совместного решения уравнений Бернулли и количества движения.
Надо, впрочем, отметить следующее. Кирхгоф, Н. Е. Жуковский и другие дали особые методы для определения размера «сжатого» сечения при истечении жидкости из различных отверстий. Эти методы основаны на теории функций комплексной переменной и относятся к плоскому безвихревому установившемуся движению идеальной невесомой жидкости. Приближенное (а в некоторых случаях и точное) использование указанных методов для определения площади ωс сжатого сечения несколько расширяет круг задач, для которых ζjможет быть найдено теоретически.
В случае квадратичной области сопротивления, которую, мы имели в виду выше, величина ζjне должна зависеть от числа Рейнольдса, а следовательно, не должна зависеть: от скорости v, от рода жидкости (т. е. от величины v), а также от размеров узла, где возникает данная местная потеря напора. Величина X,tдолжна зависеть практически только от геометрической формы упомянутого узла.
Заметим, что в случае доквадратичной области сопротивления или в случае ламинарного режима движения жидкости в трубах (этих случаев мы выше вовсе не касались) величина ζj– оказывается зависящей от числа Рейнольдса, а следовательно, от величин v и v и размеров потока (а также, разумеется, и от геометрической формы рассматриваемого узла). В связи с этим расчеты местных потерь в указанных случаях получаются более сложными.
В заключение подчеркнем, что приведенные выше значения ζj относятся к условиям, когда расстояния между узлами, для которых определяются hj, достаточно велики, т. е. такие, что один узел практически не влияет на кинематическую картину движения жидкости в пределах другого узла.
СОКРАЩЕННЫЕ СПРАВОЧНЫЕ ДАННЫЕ
О ВЕЛИЧИНЕ КОЭФФИЦИЕНТА МЕСТНОГО СОПРОТИВЛЕНИЯ Х,}
(В СЛУЧАЕ УСТАНОВИВШЕГОСЯ НАПОРНОГО ТУРБУЛЕНТНОГО
ДВИЖЕНИЯ ЖИДКОСТИ)
Выше были рассмотрены следующие случаи местных потерь напора hj: 1) резкое расширение трубы (см. стр. 183); 2) выход из трубы (см. стр. 187); 3) постепенное расширение трубы (см. стр. 188); 4) сужение трубопровода и вход в трубопровод (см. стр. 190).
Далее приводятся эмпирические данные,[44] служащие для определения коэффициента местного сопротивления ζj, входящего в формулу Вейсбаха (4-154) и относящегося к другим местным потерям. Общее обозначение коэффициента ζj, далее заменяется частными его обозначениями: ζд (коэффициент, относящийся к диафрагме), ζ р.пов (коэффициент, относящийся к резкому повороту трубы) и т. д.
§
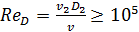 и при
и при 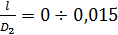 (рис. 4-37):
(рис. 4-37):
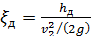 ,
,
где v2— средняя скорость в круглом отверстии диафрагмы площадью ω2. Величина ζд берется из табл. 4-5 в зависимости от отношений ω2/ω1, и ω2/ω3 (обозначения ω1 и ω3 см. на чертеже).
2°. Резкий поворот трубы иа угол θ; рис. 4-38, а:
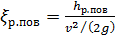 ,
,
где величина коэффициента сопротивления резкого поворота  для гладких труб круглого и квадратного поперечного сечения вычисляется по формуле
для гладких труб круглого и квадратного поперечного сечения вычисляется по формуле
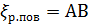 , (4-156)
, (4-156)
причем здесь эмпирические коэффициенты А и В берутся (согласно И. Е. Идельчику) из табл. 4-6 и 4-7.
Рис. 4-37. Диафрагма
3°. Плавный поворот трубы на угол θ(при ReD≥2∙105); рис. 4-38,б:
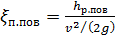 ,
,
где величина коэффициента сопротивления плавного поворота  для гладкой цилиндрической грубы вычисляется по формуле
для гладкой цилиндрической грубы вычисляется по формуле
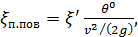 (4-157)
(4-157)
причем здесь  берется из табл. 4-8, составленной по данным Вейсбаха.
берется из табл. 4-8, составленной по данным Вейсбаха.
4°. Тройник вытяжной (рис. 4-39); ω1 = ω2. Коэффициенты сопротивления ζ2-3 и ζ′2-3. учитывающие снижение[45] (изменение) напора (h)2-3 от сечения 2 – 2 до сечения 3-3;
где  находится по табл. 4-9 в зависимости от отношений ω2/ω3 и Q2/Q3 (обозначения указаны на чертеже)
находится по табл. 4-9 в зависимости от отношений ω2/ω3 и Q2/Q3 (обозначения указаны на чертеже)
Рис. 4-38. Поворот трубы
Коэффициенты сопротивления  и
и 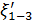 , учитывающие снижение напора
, учитывающие снижение напора 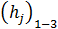 от сечения 1 -1 до сечения 3 — 3 (рис. 4-39)
от сечения 1 -1 до сечения 3 — 3 (рис. 4-39)
где  находится по табл. 4-10 в зависимости от отношения
находится по табл. 4-10 в зависимости от отношения 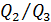 .
.
Таблица 4-5
§
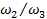 , , | 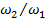 | ||||||||||
| 0.1 | 0.2 | 0,3 | 0.4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| 2.90 | 2,80 | 2,67 | 2,53 | 2,40 | 2,25 | 2,09 | 1,98 | 1,75 | 1.50 | 1.00 | |
| 0.2 | 2.27 | 2,17 | 2,05 | 1,94 | 1,82 | 1.69 | 1,55 | 1.40 | 1.26 | 1,05 | 0,64 |
| 0.4 | 1.70 | 1,62 | 1,52 | 1,42 | 1,32 | 1,20 | 1,10 | 0,98 | 0,85 | 0,68 | 0,36 |
| 0,6 | 1.23 | 1,15 | 1.07 | 0,98 | 0,90 | 0.80 | 0,72 | 0,62 | 0.52 | 0,39 | 0,16 |
| 0,8 | 0.82 | 0.76 | 0.69 | 0.63 | 0,56 | 0,49 | 0.42 | 0,35 | 0,28 | 0,18 | 0,04 |
| 1.0 | 0.50 | 0,45 | 0,40 | 0,35 | 0,30 | 0,25 | 0,20 | 0,15 | 0,10 | 0,05 |
Таблица 4-6
Значения коэффициента А к формуле (4-156)
| θ° | |||||||||||
| А | – | 2,50 | 2,22 | 1,87 | 1,50 | 1,28 | 1,20 | 1,20 | 1,20 | 1,20 | 1,20 |
Таблица 4-7
Значение коэфициента В к формуле (4-156)
| θ° | ПО | ||||||||||
| В | 0,05 | 0,07 | 0,17 | 0,37 | 0,63 | 0,99 | 1,56 | 2,16 | 2,67 | 3,00 |
Таблица 4-8
Значения коэффициента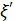 к формуле (4-157)
к формуле (4-157)
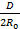 0 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0,7 | 0,8 | 0,9 | 1.0 |
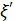 | 0,13 | 0,14 | 0,16 | 0,21 | 0,29 | 0,44 | 0,66 | 0,98 | 1,41 | 1,98 |
Таблица 4-9
Значения коэффициента сопротивления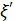 вытяжного тройника (рис. 4-39)
вытяжного тройника (рис. 4-39)
 | 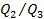 | |||||||||
| 0,1 | 0.2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0.9 | 1,0 | |
| 0,09 | -0,50 | 2,97 | 9,90 | 19,70 | 32,40 | 48,80 | 66,50 | 86,90 | 110,00 | 136,00 |
| 0,19 | -0,53 | 0,53 | 2,14 | 4,23 | 7,30 | 11,40 | 15,60 | 20,30 | 25,80 | 31,80 |
| 0,27 | -0,59 | 0.00 | 1,11 | 2.18 | 3,76 | 5,90 | 8,38 | 11,30 | 14,60 | 18,40 |
| 0,35 | -0,65 | -0,09 | 0,59 | 1,31 | 2,24 | 3,52 | 5,20 | 7,28 | 9,23 | 12,20 |
| 0,44 | -0,80 | -0,27 | 0,26 | 0,84 | 1,59 | 2,66 | 4,00 | 5,73 | 7,40 | 9,12 |
| 0,55 | -0,88 | -0,48 | 0,00 | 0,53 | 1,15 | 1,89 | 2,92 | 4,00 | 5,36 | 6,60 |
| 1.00 | -0.65 | -0.40 | -0.24 | 0.10 | 0,50 | 0,83 | 1.13 | 1.47 | 1,86 | 2,30 |
Таблица 4-10
Значения коэффициента сопротивления ζ1-3 Для вытяжного тройника (рис. 4-39)
| Q2/Q1* | 0,1 | 0,2 | 0.3 | 0,4 | 0,5 | 0,6 | 0,7 | 0.8 | 0,9 | 1,0 |
| ζ1-3 | 0,70 | 0,64 | 0.60 | 0,65 | 0,75 | 0,85 | 0,92 | 0.96 | 0,99 | 1,00 |
Таблица 4-11
Значения коэффициента сопротивления ζ1-2 для приточного тройника (рис. 4-40)
| ω2/ω1 | Q2/Q1 | |||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1.0 | |
| 0,09 0,19 0.27 0,35 0,44 0,55 1.00 | 2,80 1,41 1,37 1,10 1,22 1,09 0.90 | 4,50 2,00 1,81 1,54 1,45 1,20 1.00 | 6,00 2,50 2,30 1,90 1,67 1,40 1.13 | 7,88 3,20 2,83 2,35 1,89 1.59 1.20 | 9,40 3,97 3,40 2,73 2,11 1,65 1,40 | 11,10 4,95 4,07 3,22 2,38 1,77 1.50 | 13,00 6,50 4,80 3,80 2,58 1,94 1.60 | 15,80 8,45 6,00 4,32 3,04 2,20 1.80 | 20,00 10,80 7,18 5,28 3,84 2,68 2.06 | 24,70 13,30 8,90 6,53 4,75 3,30 2.30 |
Таблица 4-12
Значения коэффициента сопротивления ζ1-3 для приточного тройника (рис. 4-40)
| Q2/Q1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0.6 | 0,7 | 0,8 | 0.9 | 1.0 |
| ζ1-3 | 0,70 | 0,64 | 0,60 | 0,57 | 0,55 | 0,51 | 0,49 | 0,55 | 0,62 | 0,70 |
1Как видно, величина ζ1-3 (при Q1 = Q2), не совпадает с соответствующей величиной ζ1-3 в табл. 4-10. Это обстоятельство объясняется неточностью опытов.
Таблица 4-13
Значения ζ3 Для простой задвижки, перекрывающей круглоцилиндрическую трубу (рис. 4-41)
| a/D | 0.2 | 0,3 | 0.4 | 0,5 | 0,6 | 0.7 | 0.8 | 0,9 | |
| Сз | – | 35.0 | 10,0 | 4.60 | 2,06 | 0,98 | 0,44 | 0.17 | 0,06 |
Таблица 4-14
Значения ζ 3 для простой задвижки, перекрывающей трубу прямоугольного сечения (рис. 4-42)
| а/с | 0,1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0,7 | 0.8 | 0.9 | |
| Сэ | – | 44,5 | 17,8 | 8,12 | 4,02 | 2,08 | 0,95 | 0,39 | 0,09 |
5°. Тройник приточный (рис. 4-40); ω1 = ω2. Коэффициенты сопротивления ζ1-2 и 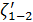 учитывающие снижение напора (hj )1-2 от сечения 1 — 1 до сечения 2 — 2
учитывающие снижение напора (hj )1-2 от сечения 1 — 1 до сечения 2 — 2
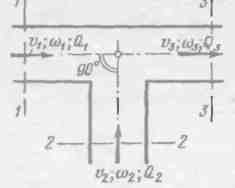
Рис. 4-39. Тройник вытяжной
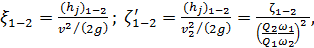
где 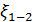 находится по табл. 4-11 в зависимости от отношений
находится по табл. 4-11 в зависимости от отношений 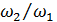 и
и 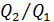 (обозначения указаны на чертеже).
(обозначения указаны на чертеже).
Коэффициенты сопротивления 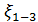 и
и 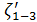 учитывающие снижение напора (hj )1-3 от сечения 1 — 1 до сечения 3—3 (рис. 4-40):
учитывающие снижение напора (hj )1-3 от сечения 1 — 1 до сечения 3—3 (рис. 4-40):
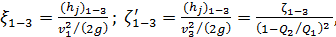
где 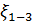 находится по табл. 4-12 в зависимости от отношения
находится по табл. 4-12 в зависимости от отношения 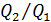 .
.
60. Задвижки:
 ,
,
где v — скорость в трубе и h3 — потеря напора от сечения 1—1 до сечения 2—2 (см., например, рис. 4-41).
Рис. 4-40. Тройник приточный
Рис. 4-41. Задвижка простая на круглой трубе
Величины 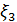 берутся:
берутся:
а) для простой задвижки, перекрывающей трубу круглого поперечного сечения (рис. 4-41), из табл. 4-13 в зависимости от отношения a/D, где а —открытие задвижки;
б) для простой задвижки, перекрывающей трубу прямоугольного поперечного сечения (рис. 4-42),— из табл. 4-14 в зависимости от отношения а/с, где с — высота трубы;
в) для задвижки Лудло (рис. 4-43) на круглой трубе — из табл. 4-15 в зависимости от степени открытия a/D задвижки;
г) для задвижки с симметричным сужением при полном ее открытии (рис. 4-44) — из табл. 4-16 в зависимости от диаметра трубы и других размеров задвижки, указанных на чертеже;
д) для дискового (дроссельного) затвора (рис. 4-45), перекрывающего круглоцилиндрическую трубу, — из табл. 4-17 в зависимости от угла θ, показанного на чертеже;
Таблица 4-15
Значения ζ3 для задвижки Лудло, перекрывающей круглоцилиидрическую трубу (рис. 4-43)
| a/D | 0,25 | 0.3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| ζ3 | 30,0 | 22,0 | 12,0 | 5,3 | 2,8 | 1,5 | 0,8 | 0,3 | 0,15 |
Таблица 4-16
Значения ζз для задвижки (при полном открытии) с симметричным сужением на круглоцилиидрической трубе (рис. 4-44)1
| D. мм | ||||
| Dс/D | 0,67 | 0,67 | 0,80 | 0,75 |
| l/D | 2.50 | 1,68 | 1.50 | 1,33 |
| ζ3 | 0,30 | 0,36 | 0,16 | 0,19 |
1 Значения ζ задвижки с симметричным сужением учитывают потери сужения и последующего расширения.
Таблица 4-17
Значения ζз для дискового (дроссельного) затвора, перекрывающего круглоцилиидрическую трубу (рис. 4-45)
| θ° | |||||||||
| ζз | – | 0,52 | 1,54 | 4,50 | 11,0 | 29,0 | – |
Таблица 4-18
Значения ζз для дискового (дроссельного) затвора, перекрывающего трубу прямоугольного поперечного сечения (рис. 4-45)
| θ° | |||||||||
| ζз | – | 0,45 | 1,34 | 3,54 | 9,30 | 25,0 | 77,0 |
Таблица 4-19
Значения ζкл для захлопни клапана (рис. 4-46)
е) для дискового (дроссельного) затвора (рис. 4-45), перекрывающего трубу прямоугольного поперечного сечения, – из табл. 4-18 в зависимости от угла θ, показанного на чертеже.
7°. Клапаны:
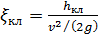 ,
,
где v — скорость в трубе и 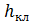 — потери напора в клапане.
— потери напора в клапане.
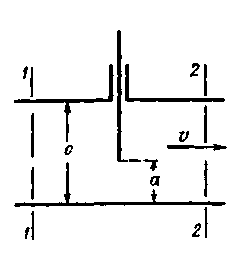
Рис. 4-42. Задвижка простая на прямоугольной трубе
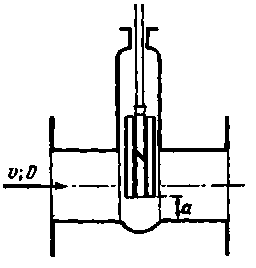
Рис.4-43. Задвижка Лудло
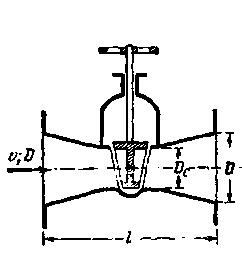
Рис. 4-44. Задвижка с сужением
Величины  берутся:
берутся:
а) для захлопки (рис. 4-46) — из табл. 4-19 в зависимости от углаθ,показанного на чертеже;
б) для обратного клапана (рис. 4-47) — по табл. 4-20 в зависимости от диаметра трубы D;
в) для всасывающего клапана с сеткой (рис. 4-48) — по табл. 4-21в зависимости от диаметра трубы.
Рис. 4-45 Дисковый затвор
Рис. 4-46. Захлопка
8°. Решетки стержневые в трубе прямоугольного поперечного сечения (рис. 4-49) при .
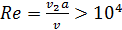 (4-158)
(4-158)
Предполагается, что стержни решетки располагаются в продольных (по отношению к потоку) вертикальных плоскостях. Следует подчеркнуть, что приводимые в этом пункте данные широко используются и для подсчета потерь напора в случае безнапорного движения воды через решетку.
Приводимые ниже данные заимствованы из [4-5].
1. Чистая (незагрязненная) решетка.
а) В случае  = 5;
= 5;  > 1,0; величина
> 1,0; величина 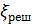 определяется по формуле Кришмера[46]
определяется по формуле Кришмера[46]
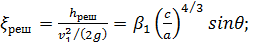 (4-159′)
(4-159′)
где v1 — средняя скорость перед решеткой; θ — угол наклона стержней решетки к горизонту;
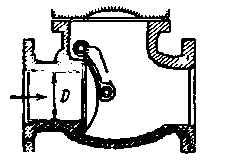
Рис. 4-47. Обратный клапан
Рис. 4-48. Всасывающий клапан с сеткой
Рис. 4-49. Решётка стержневая
а-ширина просвета между стержнями; с – толщина стержня; l-больший размер поперечного сечения стержня решетки (см. рис. 4-50);β1 — коэффициент, принимаемый по табл. 4-22 в зависимости от формы поперечного сечения стержней решетки
Рис. 4-50. Типы стержней (к рис. 4-49)
Таблица 4-20
Значения ζкл для обратного клапана (рис. 4-47)
| D, мм | |||||||
| ζкл | 1,3 | 1.4 | 1,5 | 1,9 | 2,1 | 2.5 | 2,9 |
Таблица 4-21
Значения ζкл для всасывающего клапана с сеткой (рис. 4-48)
| D, мм | |||||||
| ζкл | 8,5 | 7,0 | 4,7 | 3,7 | 2,5 | 1,6 |
Таблица 4-22
Значения коэффициента β1 формуле (4-159)
| Номера стержней | |||||||
| Pi | 2,34 | 1,77 | 1,77 | 1,00 | 0,87 | 0,71 | 1,73 |
Таблица 4-23
Значения коэффициента β2 к формуле (4-160)
| Номера стержней | |||||||
| Р2 | 1,0 | 0,76 | 0,76 | 0,43 | 0,37 | 0,30 | 0,74 |
Таблица 4-24
Значения коэффициента ζ′ к формуле (4-160)
 | ω2/ω1 | |||||||||||||||
| 0,02 | 0,04 | 0,06 | 0,08 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0.90 | 1,0 | |
| 96,0 | 51,5 | 30,0 | 18,2 | 8,25 | 4,00 | 2,00 | 0,97 | 0,42 | 0,13 | |||||||
| 0,2 | 94,0 | 48,0 | 28,0 | 17,4 | 7,70 | 3,75 | 1,87 | 0,91 | 0,40 | 0,13 | 0,01 | |||||
| 0,4 | 89,0 | 46,0 | 26,5 | 16,6 | 7,40 | 3,60 | 1,80 | 0,88 | 0,39 | 0,13 | 0,01 | |||||
| 0,6 | 81,0 | 42,0 | 24,0 | 15,0 | 6,60 | 3,20 | 1,60 | 0,80 | 0,36 | 0,13 | 0,01 | |||||
| 0,8 | 66,0 | 34,0 | 19,6 | 12,2 | 5?50 | 2,70 | 1,34 | 0,66 | 0,31 | 0,12 | 0,02 | |||||
| 1,0 | 60,0 | 31,0 | 17,8 | 11,1 | 5,00 | 2,40 | 1,20 | 0,61 | 0,29 | 0,11 | 0,02 | |||||
| 1,4 | 55,6 | 28,4 | 16,4 | 10,3 | 4,60 | 2,25 | 1,15 | 0,58 | 0,28 | 0,11 | 0,03 | |||||
| 2,0 | 53,0 | 27,4 | 15,8 | 9,9 | 4,40 | 2,20 | 1,13 | 0,58 | 0,28 | 0,12 | 0,04 | |||||
| 3,0 | 53,5 | 27,5 | 15,9 | 10,0 | 4,50 | 2,24 | 1,17 | 0,61 | 0,31 | 0,15 | 0,06 | |||||
| 4,0 | 53,8 | 27,7 | 16,2 | 10,0 | 4,60 | 2,25 | 1,20 | 0,64 | 0,35 | 0,16 | 0,08 | |||||
| 5,0 | 55,5 | 28,5 | 16,5 | 10,5 | 4,75 | 2,40 | 1,28 | 0,69 | 0,37 | 0,19 | 0,10 | |||||
| 6,0 | 55,8 | 28,5 | 16,6 | 10,5 | 4,80 | 2,42 | 1,32 | 0,70 | 0,40 | 0,21 | 0,12 | |||||
| 7,0 | 55,9 | 29,0 | 17,0 | 10,9 | 5,00 | 2,50 | 1.38 | 0,74 | 0,43 | 0,23 | 0,14 | |||||
| 8,0 | 56,0 | 30,0 | 17,2 | 11,1 | 5,10 | 2,58 | 1,45 | 0,80 | 0,45 | 0,25 | 0,16 | |||||
| 9,0 | 57,0 | 30,0 | 17,4 | 11,4 | 5,30 | 2,62 | 1,50 | 0,82 | 0,50 | 0,28 | 0,18 | |||||
| 10,0 | 59,7 | 31,0 | 18,2 | 11,5 | 5,40 | 2,80 | 1,57 | 0,89 | 0,53 | 0,32 | 0,20 |
(различные формы этих сечений за соответствующими номерами показаны на рис. 4-50).
б) В случае отношений 1/с и а/с любой величины
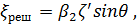 (4-159′′)
(4-159′′)
где θ — угол наклона стержней к горизонту; коэффициент β2 берется из табл. 4-23 в зависимости от формы поперечного сечения стержней; коэффициент 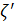 — из табл. 4-24 в зависимости от отношения ω2/ω1и отношения l/d’; здесь ω1— площадь живого сечения перед решеткой; ω2 — полная площадь решетки в свету; d‘ — величина, равная:
— из табл. 4-24 в зависимости от отношения ω2/ω1и отношения l/d’; здесь ω1— площадь живого сечения перед решеткой; ω2 — полная площадь решетки в свету; d‘ — величина, равная:
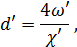
где ω’ — площадь одного отверстия решетки; 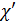 — смоченный периметр этого отверстия.
— смоченный периметр этого отверстия.
2. Загрязненная решетка (в случае гидротехнического сооружения):
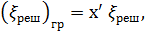
где 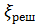 определяется, как указано выше (в п. 1); численное значение коэффициента х’ принимается равным:
определяется, как указано выше (в п. 1); численное значение коэффициента х’ принимается равным:
а) при машинной очистке решетки х′ = 1,1÷1,3;
б) при ручной очистке решетки х’ = 1,5 ÷ 2,0.
3.Решетка (гидротехнического сооружения) с дополнительным каркасом,
состоящим из добавочных горизонтальных стержней:
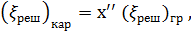
где коэффициент х” определяется по формуле
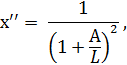
где L— высота решетки в свету (рис. 4-49); А — суммарная высота поперечных элементов:
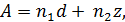
где n1 – количество распорно-связных горизонтальных элементов (высотой d); n2 — количество промежуточных опорных балок (высотой z).
§
1°. Условия протекания жидкости в пределах поворота трубы. На повороте трубы получаем искривление линий тока (рис. 4-36,6). На частицы жидкости, движущиеся по искривленным линиям тока, действует центробежная сила инерции. За счет этой силы гидродинамическое давление (а следовательно, и потенциальная энергия) в месте поворота у внешней стенки трубы повышается, а у внутренней — понижается. Это же обстоятельство обусловливает уменьшение скоростного напора (удельной кинетической энергии) у внешней стенки и увеличивает его у внутренней стенки. Таким образом, на повороте происходит перераспределение скоростей по живым сечениям и деформация эпюр скоростей вдоль потока (как показано на рис. 4-36, б)
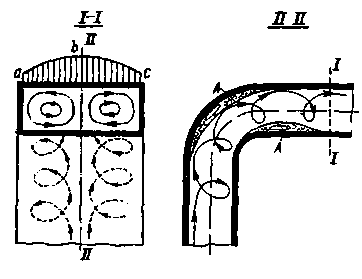
Рис. 4-51. Течение на повороте трубы
На рис. 4-36, б показан отрыв транзитной струи в двух местах. Надо заметить, что отрыв струи от внутренней стенки увеличивается за счет инерции частиц жидкости, движущихся вдоль этой стенки (в пристенном слое по пути от сечения 1—1 до точки с).
При плавном повороте трубы указанные отрывы струи могут отсутствовать. В этом случае местные потери напора в значительной мере обусловливаются имеющимся на повороте «парным вихрем» (винтовым движением, вызванным действием сил инерции). Такое винтовое движение, характеризуемое наличием так называемой поперечной циркуляции (иначе «вторичными течениями»), показано на рис. 4-51, где для примера изображена прямоугольная труба. На этом чертеже показана эпюра давления на стенку трубы, ограниченная кривой abc. Как видно, в центральной части внешней стенки трубы давление оказывается наибольшим (в связи с большими скоростями и в этой части трубы). Такое положение и обусловливает движение жидких частиц влево и вправо (вдоль внешней стенки) от центральной части к периферии.
2°. Соединение потоков (рис. 4-52).[47] В этом случае получаем «поверхность раздела» а — б. Благодаря турбулентному перемешиванию «ступенчатая» эпюра скоростей, получающаяся в сечении АВ (эта эпюра на рисунке не показана), выравнивается на длине l и приобретает в сечении 2 — 2 «нормальный» вид. Через поверхность раздела а — б (в связи со сказанным в § 3-16) должна передаваться удельная энергия ΔЕ. Между сечениями 1—1 и 2—2 могут возникать отрывы струи от стенки русла, в связи с чем будут появляться водоворотные области.
Наличие сил трения в жидкости обусловливает: а) неравномерное распределение скоростей в сечениях 1, 2 и 3; б) передачу энергии жидкости через поверхность раздела а — б (от 1-го потока к 3-му или наоборот от 3-го потока к 1-му потоку); в) диссипацию энергии, а следовательно, уменьшение энергии по течению. Для простоты пояснения пренебрежем этими обстоятельствами (обстоятельствами а, б, в), причем условно будем считать, что в пределах рассматриваемого небольшого участка потока (между сечениями 1 — 1, 2 — 2, 3—3) жидкость является идеальной.
Принимая такое допущение, можем в соответствии с законом сохранения энергии написать следующее энергетическое уравнение
 (4-161)
(4-161)
где Q1, Q2 и Q3 — расходы жидкости для отдельных труб (см. рисунок); 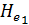 ,
,  напоры (полные удельные энергии) соответственно в сечениях 1, 2 и 3.
напоры (полные удельные энергии) соответственно в сечениях 1, 2 и 3.
Из уравнения (4-161), учитывая, что
Q1 Q3 = Q2 (4-162)
легко получить зависимость (для идеальной жидкости на пути от сечения 1 — 1 до сечения 2—2):
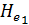 =
= 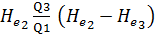 (4-163)
(4-163)
Из рассмотрения этой зависимости видно следующее:
1) При Q3 = 0, т. е. при отсутствии присоединения расхода, в случае идеальной жидкости 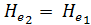 ,, , что и должно быть согласно уравнению Бернулли.
,, , что и должно быть согласно уравнению Бернулли.
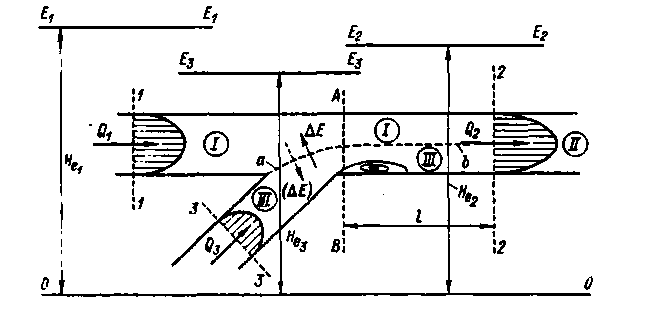
Рис. 4-52. Схема соединения двух потоков
2) Если Q3 ≠ 0, т. е. если мы имеем по длине потока переменный расход (Q ≠ const), то для идеальной жидкости получим 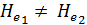 причем могут иметь место случаи, когда оказывается, что
причем могут иметь место случаи, когда оказывается, что 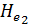 >
> 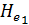 т. е. напор (полная удельная энергия) по течению идеальной жидкости увеличивается.
т. е. напор (полная удельная энергия) по течению идеальной жидкости увеличивается.
Отмеченные положения (см. пп. 1 и 2) вытекают из рассмотрения закона сохранения энергии. Здесь необходимо помнить, что уравнение Бернулли (3-101) справедливо только для частного случая, когда по длине потока расход Q является постоянным (Q = const).
Если бы мы рассматривали в данном узле не идеальную жидкость, а реальную, то в принципиальном отношении у нас ничего бы не изменилось (имели бы место только количественные, но не качественные изменения).
В случае идеальной, а также реальной жидкости, напорные линии Е— Е в рассматриваемом узле потока могут располагаться, как показано на рис. 4-52; как видно, переходя от потока III к потоку II, мы можем получить для реальной жидкости увеличение полноте напора по течению ( 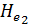 >
> 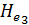 ).
).
3°. Разделение потоков.[48] Чтобы разъяснить отмеченный выше «парадокс», рассмотрим разделение потока (рис. 4-53).
Построим для сечения 1 — 1 (см. на рисунке живое сечение abcde) эпюру напоров 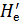 (относящихся к элементарным струйкам, составляющим рассматриваемый поток):
(относящихся к элементарным струйкам, составляющим рассматриваемый поток):
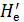 = z
= z 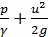 , (4-164)
, (4-164)
где (z  ) = const для данного живого сечения а—е.
) = const для данного живого сечения а—е.
Такая эпюра выражается на рисунке площадью a-b-c-d-e-a.[49] Осредняя ординаты этой эпюры в пределах всего живого сечения 1—1 потока, получаем напор 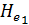 [см. 1 зависимость (3-100)]:
[см. 1 зависимость (3-100)]:
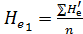 , (4-165)
, (4-165)
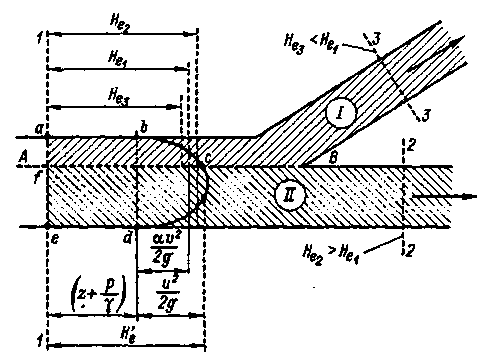
Рис. 4-53. Схема разделения потока на две(I и II части)
Эпюры напоров 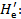 1-(abcfa) – для сечения af; 2 – (fcdef)-для сечения ef; 3-(abcdea)- для всего живоо сечения ae
1-(abcfa) – для сечения af; 2 – (fcdef)-для сечения ef; 3-(abcdea)- для всего живоо сечения ae
Выделим теперь на рис. 4-53 линией АВ две части рассматриваемого потока I к II (эти части на рисунке покрыты штриховкой разного наклона): При этом можем отметить следующее:
а) эпюра напоров Н’е для I части / потока выражается площадью abcfa; осредняя напоры Н’е в пределах части af живого сечения, получаем напор Не3 (см. рисунок), меньший чем Не1:
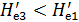 (4-166)
(4-166)
б) эпюра напоров Н’едля I части II потока выражается площадью fcdef; осредняя напоры Н’eв пределах части fе живого сечения, получаем напор Не2больший чем напор Не1 :
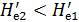 (4-167)
(4-167)
Таким образом полный напор для целого потока реальной жидкости может изменяться по течению не только в связи с «потерей напора» (обусловленной работой сил трения), но также еще и в связи с отделением (или присоединением) на пути от сечения 1 — 1 и до сечения 2 —2 соответствующих масс жидкости.
В связи со сказанным, рассматривая выше местные потери напора в тройниках (стр. 195), мы различаем «коэффициент потерь напора» («коэффициент сопротивления») и «коэффициент изменения напора».
§
Представим на рис. 4-54 элементарную струйку и ее поперечное сечение 1—1. Обозначим через V объем жидкости, проходящий за некоторое время t0 через сечение струйки 1—1. При этом вес этого объема G = γV, а масса М = ρV= 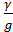 V; механическую энергию жидкости, принадлежащую объему V, обозначим через Еv.
V; механическую энергию жидкости, принадлежащую объему V, обозначим через Еv.
Выше величину Ev мы относили к единице веса жидкости. Однако, вообще говоря, величину Ev можно относить также и к единице объема, и к единице массы движущейся жидкости. Слова «удельная величина» следует понимать здесь, как «относительная величина», т.е. величина, отнесенная к чему-либо (например, к объему жидкости или к весу этого объема или к массе этого объема).
В связи со сказанным, можно написать три разных выражения для удельной энергии движущейся жидкости (энергии, отнесенной к единице веса, к единице объема и к единице массы); эти выражения получают следующий вид (где L, t, P — символы соответственно длины, времени и силы):
1) мера энергии, принадлежащей единице веса движущейся жидкости
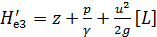 (4-168)
(4-168)
достаточно Н’еумножить на вес объема V и мы получим механическую энергию этого объема жидкости;
2) мера энергии единицы объема жидкости:
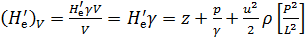 (4-169)
(4-169)
3) мера энергии единицы массы жидкости
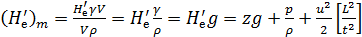 (4-170)
(4-170)
достаточно (H’е)тумножить на массу объема V и мы получим механическую энергию этого объема. Можно написать:
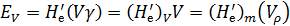 (4-171)
(4-171)
где величины Н’е, (H’e)vи (Н’е)тявляются соответствующими напорами. В связи с наличием сил трения в реальной жидкости величина Evпо течению должна уменьшаться.
Перейдем к рассмотрению целого потока реальной жидкости, причем величину Q будем считать постоянной вдоль течения: Q = const.
Будем пользоваться понятием только двух напоров Н’еи (Н’е)т[напора (Н’е)у касаться не будем]. При этом можем написать следующие три вида уравнения Бернулли, из которых каждый вид этого уравнения будет относиться к определенному случаю движения жидкости:
1-й вид: обший случай установившегося движения жидкости, когда жидкость является относительно тяжелой, т. е. [см. уравнение (4-170)] величиной (zg) нельзя пренебрегать сравнительно с величиной 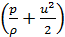 . В этом случае получаем обычное уравнение Бернулли:
. В этом случае получаем обычное уравнение Бернулли:
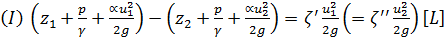 (4-172)
(4-172)
где ζ – безразмерные «коэффициенты сопротивления»;
2-й вид: частный случай установившегося движения жидкости, когда жидкость является относительно легкой, т. е. когда величиной (zg) следует пренебречь сравнительно с величиной 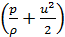 . В этом случае, исходя из уравнения (4-170) получаем:
. В этом случае, исходя из уравнения (4-170) получаем:
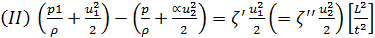 (4-173)
(4-173)
можно сказать, что здесь мы пренебрегаем работой силы тяжести по сравнению с работой сил трения;
3-й вид: частный случай предыдущего вида движения, когда мы имеем равномерное движение, т. е. v1= v2(жидкость легкая, причем v = const вдоль течения):
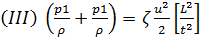 (4-174)
(4-174)
Рассматривая полученные выше три вида уравнения Бернулли, подчеркнем следующие два важных обстоятельства:
1-е обстоятельство: легко показать, что при идентичных условиях безразмерные коэффициенты сопротивления 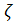 , входящие в уравнения (4-173) и (4-174), численно равны соответствующим коэффициентам, входящим в уравнение (4-172).[50]
, входящие в уравнения (4-173) и (4-174), численно равны соответствующим коэффициентам, входящим в уравнение (4-172).[50]
2-е обстоятельство: напор Не в отличне от напоров (Не)V и (Не)m имеет размерность длины. Поэтому очень важную геометрическую интерпретацию уравнения Бернулли удобно (физически доходчиво) проводить, пользуясь именно величиной напора Н’е, а не {Н’е)V или (Н’е)m; кроме того, пользуясь величиной Н’е, мы можем удобно использовать пьезометрические трубки и трубки Пито для выполнения соответствующих замеров.
Дополнительно из рассмотрения уравнений (4-172), (4-173) и (4-174) можно сделать следующие существенные выводы:
1) в случае «реальной» жидкости, обладающей достаточно большой величиной у (например, в случае воды) напор Не в нижерасположенном (по течению) живом сечении (сечении 2—2) всегда должен быть меньше, чем напор Не в вышерасположенном живом сечении (в сечении 1—1); при этом, как видно, движение «тяжелой» жидкости оказывается направленным в сторону меньшей величины Нe, но не в сторону области, характеризуемой меньшим давлением р; в данном случае давление р во «втором сечении» может быть и меньшим и большим, чем в «первом сечении»;
2) в случае реальной жидкости, обладающей малым удельным весом (например, в случае движения воздуха), соответствующий напор в нижерасположенном (по течению) живом сечении (сечении 2 — 2) также должен быт меньшим, чем напор в вышерасположенном живом сечении (1 — 1), но давление р в сечении 2—2 может быть большим Можно утверждать, что движение «легкой» жидкости оказывается направленным в сторону области с меньшей величиной напора:
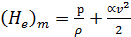 (4-175)
(4-175)
а не в сторону области меньшего давления р;
3) только в случае равномерного движения «легкой» жидкости (например, равномерного движения воздуха) движение жидкости [см. зависимость (4-174)], оказывается направленным в сторону меньшего давления р.
Дополнительное замечание:
1) Рассмотрим невесомую жидкость. В этом случае в уравнении Бернулли следует полагать g = 0, а следовательно, и gz = 0. При этом приходится пользоваться понятием напора  как энергии, отнесенной к единице массы. Как видно, мы получаем |следующие выражения для такого напора (пренебрегая коэффициентом а):
как энергии, отнесенной к единице массы. Как видно, мы получаем |следующие выражения для такого напора (пренебрегая коэффициентом а):
а) в случае гидродинамик
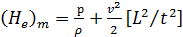 (4-176)
(4-176)
б) в случае гидростатики:
 (4-177)
(4-177)
Эти формулы выражают меру энергии, принадлежащей единице массы рассматриваемого объема невесомой жидкости.
2) Известно, что в случае конической расходящейся короткой трубы при истечении из нее «тяжелой жидкости» в атмосферу мы получаем напорную и пьезометрическую линии (линии ЕЕ и РР) в виде, изображенном на рис. 4-55, a (на этом рисунке изображены линии ЕЕ и РР для случая идеальной и для случая реальной тяжелой жидкости).
Рис 4-55. Истечение из расширяющейся конической трубы: а — «тяжелой» жидкости 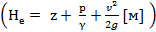 ; б — «легкой» (или невесомой) жидкости
; б — «легкой» (или невесомой) жидкости 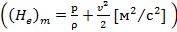
Е – E — напорная линия: Р — Р — пьезометрическая линия; -для идеальной жидкости; – для реальной жидкости
В случае легкой (или невесомой) жидкости изображать соответствующие линии ЕЕ и РР приходится уже не на той схеме, где изображена сама короткая труба, а на другом чертеже: на графике, где по вертикали откладываются величины, имеющие размерность не длины, а размерность 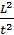 ; см. рис. 4-55, б. Этот чертеж (для идеальной и для реальной жидкости) строится в соответствии с уравнением (4-173).
; см. рис. 4-55, б. Этот чертеж (для идеальной и для реальной жидкости) строится в соответствии с уравнением (4-173).
[1] При турбулентном движении отмеченное условие обычно может быть удовлетворено, когда мы имеем однородную (одинаковую) шероховатость по всей длине смоченного периметра русла
[2] Точнее говоря, возникающая на поверхности соприкасания жидких слоев друг с другом.
[3] Коэффициент вязкости обозначают иногда не буквой η, а буквой μ.
[4] Здесь можно поступить и иначе: вместо того, чтобы вводить в формулу (4-22) абсолютное значение 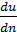 , можем условиться всегда проводить нормаль n от поверхности S в сторону возрастающих скоростей.
, можем условиться всегда проводить нормаль n от поверхности S в сторону возрастающих скоростей.
[5] Пользуясь так называемым обобщенным законом Ньютона (здесь не приводимым), можно показать, что зависимость (4-24) выражает также и касательные напряжения для площадок, взятых в плоскости живых сечений. Из механики твердого тела известно, что касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, должны быть равны между собой по величине.
[6] Наличие такой (нулевой) скорости на стенке (даже абсолютно гладкой) можно, по-видимому, в какой-то мере объяснить, используя модель «твердой воды» (см. конец § 1-4).
[7] Зависимость (4-26) написана в предположении, что величина 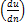 во всех точках поверхности S0 одинакова. В противном случае имеем:.
во всех точках поверхности S0 одинакова. В противном случае имеем:. 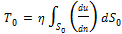 .
.
[8] Схема водоворотов а, b, с на чертеже показана упрощенной. Можно представить себе вращение жидкости и по схеме более сложной (см., например, водоворот d).
[9] Индекс «а» у скорости uа — первая буква слова «актуальная».
[10] Принятые направления Ах и Az не обязательно горизонтальны или вертикальны. Строго говоря, скорость иаследовало бы разлагать не на два, а на три направления и оперировать тремя проекциями: (иа)x, (иа)z и (иа)у. Мы же для простоты пояснения рассматриваем как бы плоскую задачу (что в действительности не имеет места).
[11] Далее, как правило, горизонтальных черточек над буквой и, а также р, ставить не будем.
[12] На рис. 4-13, а для примера показан случай интенсивной турбулентности, когда в некоторые моменты времени актуальные скорости оказываются направленными даже в сторону, противоположную общему движению.
[13] Предполагается, что площади эпюр №1 и №2 должны быть равны.
[14] Замену поперечных скоростей uzкасательными напряжениями иногда поясняют на следующем примере. Представим себе, что по реке движутся рядом (в данный момент времени), но с разными скоростями два судна, нагруженные камнями. Положим, что камни с судна, идущего с меньшей скоростью, перебрасываются на судно, идущее с большой скоростью, и наоборот: камни с судна, движущегося с большей скоростью, перебрасываются на судно, идущее с меньшей скоростью. Ясно, что в результате такой переброски камней судно, идущее с большей скоростью (получив некоторое количество камней, обладающих небольшими поступательными скоростями, равными скорости судна, идущего с малой скоростью) будет, в связи с инерцией переброшенных камней, замедлять свой -ход; судно же, идущее с меньшей скоростью — ускорять свой ход.
Ясно также, что тот же самый эффект мы можем получить не перебрасывая камни с одного судна на другое, а введя между бортами двух рассмотренных судов силу трения (являющуюся парной) определенной величины; такое воображаемое трение будет способствовать замедлению быстро идущего судна и ускорению медленно идущего судна
[15] Чтобы определить необходимую величину τт, используют как бы постулат, который условно можно представить такой записью:
[16] Вывод этой формулы приведен петитом [4-11].
[17] Далее вертикальные черточки у 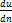 опускаем, считая, что ось n всегда направлена
опускаем, считая, что ось n всегда направлена
в сторону увеличивающихся скоростей u.
[18] Иногда динамический коэффициент турбулентной вязкости обозначается буквой А.
[19] При этом обтекание выступов шероховатости происходит с отрывом струи от них (см далее § 4-14).
[20] Эта степенная формула является несколько менее точной, чем формулы, дающие логарифмический закон распределения скоростей. Зависимость типа (4-64) применялась
и ранее, как чисто эмпирическая (с постоянным коэффициентом m) для расчета скоростей в реках.
[21] В другой форме подобная зависимость еще ранее предлагалась Г. В. Железняковым для квадратичной области сопротивления — для течения воды в реках (безиспользования коэффициента λ).
[22] Ниже будем рассматривать только верхнюю поверхность пластинки.
[23] Небольшой площадью ΔΩ этой эпюры, обусловленной некоторой перестройкой набегающего потока (диктуемой уравнением неразрывности), пренебрегаем.
[24] В этой области реальная жидкость движется как твердое тело (см. рис. 3-4, а).
[25] При достаточно равномерном распределении τ0 по смоченному периметру
[26] График, показанный на рис. 4-25, опытным путем был Получен также рядом других авторов: Муди (в 1944 г.), Г. А. Муриным (в 1948 г.) и др.
[27] Эти данные в сокращенном виде заимствованы из книги [4-4].
[28] По этому вопросу см. дополнительно статью Н. А. Картвелишвили, Сборник научно-методических статей по гидравлике. Вып. 3. — М.: Высшая школа, 1979.
[29] Ниже «черту осреднения» над величинами Δ и 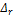 не ставим.
не ставим.
[30] Экспериментальную проверку этой формулы выполнил И. И. Агроскин [4-11, с. 145].
[31] Для различных теоретических исследований наиболее удобной является формула Маннинга степенного типа.
[32] В [4-9 и 4-10] приводятся фотографии различных русел с указанием рекомендуемых для них численных значений п. Эти фотографии в некоторой мере могут облегчить выбор величины п для данного конкретного случая.
[33] Вывод этого выражения для Ф, исходя из обычных «гидравлических представлений», приводится в статье В. Н. Цепилова «Функция диссипации механической энергии для решения обычных задач гидравлики (о работе сил внутреннего трения в жидкости)». Сборник научно-методических статей по гидравлике. Вып. № 5. — М.: Высшая школа, 1982.
[34] Часто эти области называют «вихревыми». Такое название неудачно, так как в пределах транзитной струи движение жидкости является также вихревым (см. § 3-4). Иногда области А называют «мертвыми зонами», что также нельзя признать удачным.
[35] Иногда участок длиной (l′в lв′′)называют участком дестабилизации потока, а участок длиной lперех — участком стабилизации потока
[36] См. рис. 8-1. При определенных условиях в районе сечения 2 — 2 у дна русла, как показывают опыты, возникает водоворотная зона (не представленная на рис. 8-1).
[37] Этого объяснения отрыва транзитной струи, даваемого нами, в литературе мы не
находим.
[38] На рис. 4-29, а показан частный случай — симметричное растекание потока.
[39] При рассмотрении наклонной трубы окончательные результаты получаются те же, что и для горизонтальной трубы.
[40]
[41] На рис. 4-30,6 и в представлена картина осредненного потока, симметричная относительно продольной оси трубопровода. В действительности, однако, в подобных случаях почти всегда получается искривление оси транзитной струи, причем водоворотные области оказываются несимметричными; часто может получиться отрыв струи только от мной стенки.
[42] Как нам представляется, достаточно надежно количественно решить вопрос об отрыве транзитной струи тяжелой реальной жидкости от стенки русла едва ли можно (в общем случае) без учета отмеченного нами «энергетического принципа». Дополнительно обратим внимание на то, что на рис. 4-30, г (и на рис. 4-29, а) имеется в виду случай, когда боковой приток энергии hΔE пристенной струйке, принадлежащей водоворотной области, меньше потерь энергии в этой струйке. Следует учитывать, что при отсутствии hΔE водоворотные области (см., например, рис. 4-29, a) существовать не могут. Только наличие hΔE обусловливает возможность возникновения и существования этих областей.
[43] Вывод формулы (4-147) см., например, [11, с. 157]
[44] Большинство этих данных взяты по книге [4-5].
[45] При рассмотрении тройников мы пользуемся термином «снижение напора» вместо термина «потеря напора» (см. § 4-19).
[46] В литературе приводится ряд предложений, уточняющих формулу (4-159′). При этом большинство авторов отмечает, что формула Киршмера дает заниженную величину потерь, напора. Иногда считают, что в правую часть этой формулы надо вводить поправочный множитель, равный 1,75 ÷ 2,00.
[47] См. Б. А. Дергаче в. Случаи увеличения полного напора по течению реальной I жидкости (для «целого потока» при установившемся движении). Сборник научно-методических статей по гидравлике. Вып. 3.—М.: Высшая школа, 1980.
[48] См. предыдущую сноску.
[49] Как видно, величины напоров для разных точек вертикального живого сечения откладываются от линии aе по горизонтали.
[50] Для доказательства справедливости этого положения достаточно: а) умножить на величину g обе части уравнения (4-172) и б) затем положить (z1g — z2g) = 0.








