Тема 4.3. удельная энергия сечения и критическая глубина
• В случае неравномерного установившегося движения жидкости в открытом канале средняя скорость V и глубина h потока изменяются вдоль движения, но не изменяются в любом сечении со временем.
• Удельная энергия сечения – это удельная энергия относительно плоскости сравнения, проведенной через наиболее низкую точку сечения:
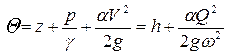 . (4.3.1)
. (4.3.1)
• Критическая глубина hcr – это глубина, при которой удельная энергия Θ сечения достигает минимального значения (рис. 4.3.1). При этом
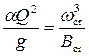 , (4.3.2)
, (4.3.2)
где 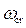 ,
, 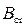 – соответственно площадь сечения и ширина потока поверху при
– соответственно площадь сечения и ширина потока поверху при 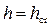 . Критическую глубину находят подбором. Вначале вычисляем значение
. Критическую глубину находят подбором. Вначале вычисляем значение 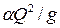 . Затем для трёх значений h находим значения
. Затем для трёх значений h находим значения 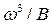 . Наносим полученные значения на график зависимость
. Наносим полученные значения на график зависимость 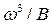 от h (рис. 4.3.2) и соединяем полученные точки плавной кривой. На пересечении этой кривой с прямой
от h (рис. 4.3.2) и соединяем полученные точки плавной кривой. На пересечении этой кривой с прямой 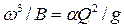 получаем значение критической глубины hcr.
получаем значение критической глубины hcr.
• Для русла прямоугольного сечения 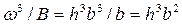 . Критическая глубина для русла прямоугольного сечения
. Критическая глубина для русла прямоугольного сечения
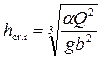 . (4.3.3)
. (4.3.3)
• Для трапецеидального сечения можно найти значение вспомогательной функции
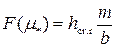 . (4.3.4)
. (4.3.4)
Потом по этому значению находят из графика рис. 4.3.3 вспомогательный параметр 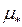 , по которому вычисляют критическую глубину:
, по которому вычисляют критическую глубину:
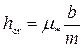 . (4.3.5)
. (4.3.5)
Пример 4.3.1. Найти критическую глубину hcr, если ширина канала по дну b = 1,5 м, коэффициент заложения откосов m = 1, коэффициент шероховатости n = 0,017, расход Q = 5 м3/с.
Решение. Вычисляем критическую глубину для русла прямоугольного сечения
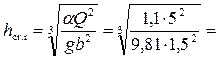 1,076 м.
1,076 м.
Находим вспомогательную функцию
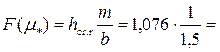 0,717.
0,717.
Из графика рис. 4.3.3 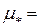 0,55.
0,55.
Критическая глубина
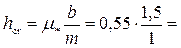 0,83 м.
0,83 м.
Решение той же задачи методом подбора в MS Excel показано на рис. 4.3.4. Получено значение hcr = 0,879 м.
• Для русел треугольного сечения B = 2mh, ω = mh2. Критическая глубина для русел треугольного сечения
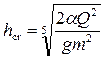 . (4.3.6)
. (4.3.6)
Пример 4.3.2. Построить график удельной энергии сечения и определить состояние потока (рис. 4.3.5). Расход Q = 0,8 м3/с, нормальная глубина h0 = 0,4 м, коэффициенты заложения откосов m1 = 1,0, m2 = 1,5, ширина русла по дну b = 0.
Решение. Средний коэффициент заложения откосов
m = (m1 m2)/2 = 1,25.
Критическая глубина
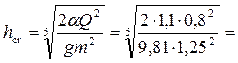 0,616 м.
0,616 м.
Поток бурный, так как h0 < hcr.
Решение примера 4.3.2 в MS Excel приведено на рис. 4.3.6.
• Для безнапорных труб круглого сечения рассчитывают расходный параметр
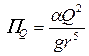 . (4.3.7)
. (4.3.7)
Потом по этому значению находят из графика рис. 4.3.7 значение  и вычисляют критическую глубину:
и вычисляют критическую глубину:
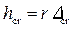 . (4.3.8)
. (4.3.8)
• При вычислениях с использованием MSExcel
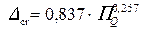 при
при  ; (4.3.9а)
; (4.3.9а)
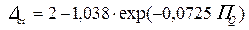 при
при 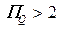 . (4.3.9б)
. (4.3.9б)
Пример 4.3.3. Найти нормальное и критическое наполнение для трубы дождевой канализации диаметром D = 600 мм при расчётном расходе Q = 430 л/с и уклоне земли i = 0,0085.
Решение. Коэффициент шероховатости канализационных труб n = 0,013.
Гидравлический радиус при наполнении доверху
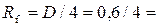 0,15 м,
0,15 м,
площадь живого сечения
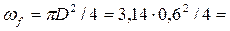 0,283 м2,
0,283 м2,
показатель степени в формуле скоростной характеристики
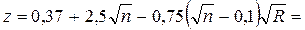
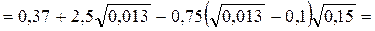 0,65,
0,65,
скоростная характеристика при наполнении доверху
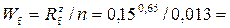 22,4 м/с,
22,4 м/с,
расходная характеристика при наполнении доверху
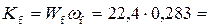 6,33 м3/с,
6,33 м3/с,
относительная расходная характеристика
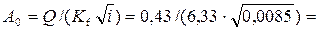 0,737.
0,737.
Из графика “рыбка” (рис. 4.2.2) нормальное наполнение 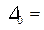 1,40.
1,40.
Расходный параметр
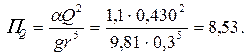
Из графика рис. 4.3.8 находим критическое наполнение
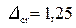 .
.
Состояние потока спокойное, так как нормальное наполнение 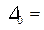 1,40 больше критического
1,40 больше критического 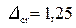 .
.
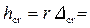 0,3·1,25 = 0,375 м.
0,3·1,25 = 0,375 м.
• Критическую глубину для русла трапецеидального сечения рассчитать проще, чем нормальную. Поэтому иногда целесообразно находить нормальную глубину с помощью показательного закона.
• Показательный закон: для двух произвольных значений глубин 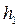 и
и 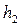 и соответствующих расходных характеристик K1 и K2 имеет вид:
и соответствующих расходных характеристик K1 и K2 имеет вид:
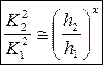 , (4.3.10)
, (4.3.10)
где x – гидравлический показатель русла, значения которого для трапецеидального и круглого сечений приведены на графике рис. 4.3.8. Для треугольных русел x = 5,4.
• Как это можно видеть на рис. 4.3.8, в каналах замкнутого сечения гидравлический показатель русла существенно изменяется уже при сравнительно небольших заполнениях. Это же касается и каналов сложенного профиля (рис. 4.3.9). Поэтому для таких каналов показательный закон при расчётах не применяется.
Пример 4.3.4. Рассчитать нормальную глубину в водоотводной канаве, если расход Q = 1,0 м3/с, коэффициент заложения откосов m = 0, ширина русла по дну b = 1 м, уклон дна ступени i = 0,0033, коэффициент шероховатости n = 0,017.
Решение. Критическая глубина для канала прямоугольного сечения
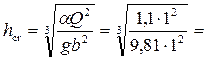 0,48 м.
0,48 м.
Площадь живого сечения 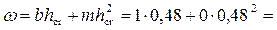 0,48 м2.
0,48 м2.
Смоченный периметр 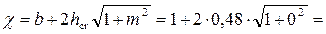 1,96 м.
1,96 м.
Гидравлический радиус R = ω/χ = 0,48/1,96 = 0,245 м.
Показатель степени в формуле скоростной характеристики
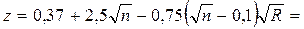
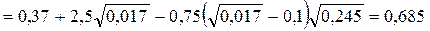 .
.
Скоростная характеристика
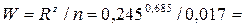 22,4 м/с.
22,4 м/с.
Расходная характеристика для критической глубины
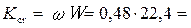 10,8 м3/с.
10,8 м3/с.
По значениям m = 0 и hcr/b = 0,48/1 = 0,48 из графика рис. 4.3.9 находим гидравлический показатель русла x = 2,7.
Расходная характеристика для сечения с нормальной глубиной
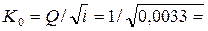 17,4 м3/с.
17,4 м3/с.
Нормальная глубина
 0,683 м.
0,683 м.
Решение той же задачи методом подбора с использованием MS Excel показано на рис. 4.3.10. Получаем h0 = 0,69 м.
• Состояние потока (бурное или спокойное) можно определить, вычислив параметр кинетичности
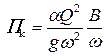 . (4.3.11)
. (4.3.11)
Поток бурный, если 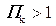 (тогда
(тогда  ), и спокойный, если
), и спокойный, если 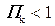 (тогда
(тогда 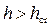 ).
).
• В случае прямоугольного сечения параметр кинетичности называется числом Фруда, которое представляет собой отношение удвоенной удельной кинетической энергии к удельной потенциальной энергии (глубине) в данном сечении:
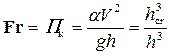 . (4.3.12)
. (4.3.12)
• Если изменять уклон i, критическая глубина 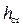 остается постоянной, а нормальная глубина, изменяясь, может при некотором значении уклона равняться критической. Критический уклон
остается постоянной, а нормальная глубина, изменяясь, может при некотором значении уклона равняться критической. Критический уклон 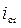 – это такой уклон, при котором критическая глубина равняется нормальной (
– это такой уклон, при котором критическая глубина равняется нормальной ( 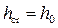 ):
):
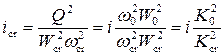 , (4.3.11)
, (4.3.11)
где 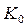 и
и 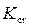 – расходные характеристики соответственно для нормальной и критической глубины.
– расходные характеристики соответственно для нормальной и критической глубины.
• Критический уклон для потока в круглых безнапорных трубах
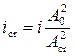 , (4.3.12)
, (4.3.12)
где 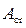 – относительная расходная характеристика при критическом наполнении;
– относительная расходная характеристика при критическом наполнении;  – относительная расходная характеристика при наполнении, которое соответствует равномерному движению (по графику “рыбка”, рис. 4.2.2) соответственно при
– относительная расходная характеристика при наполнении, которое соответствует равномерному движению (по графику “рыбка”, рис. 4.2.2) соответственно при 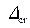 и
и 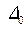 ).
).

Рис. 4.3.11. Схема расчёта критической и нормальной глубин.
§
• Основное дифференциальное уравнение установившегося неравномерного движения жидкости в открытых руслах:
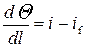 , (4.4.1)
, (4.4.1)
где 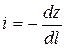 – уклон дна русла (он положителен в случае уменьшения отметок дна),
– уклон дна русла (он положителен в случае уменьшения отметок дна),  – уклон трения, т.е. потери энергии сечения по длине, отнесенные к единице длины (частный случай гидравлического уклона J). Энергия сечения возрастает за счёт уменьшающейся потенциальной энергии гравитационного поля и уменьшается вследствие потерь энергии на преодоление сил трения.
– уклон трения, т.е. потери энергии сечения по длине, отнесенные к единице длины (частный случай гидравлического уклона J). Энергия сечения возрастает за счёт уменьшающейся потенциальной энергии гравитационного поля и уменьшается вследствие потерь энергии на преодоление сил трения.
• В случае равномерного движения 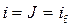 и поэтому
и поэтому
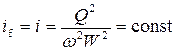 , (4.4.2)
, (4.4.2)
в случае неравномерного
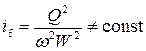 . (4.4.3)
. (4.4.3)
• Основное дифференциальное уравнение плавноизменяющегося движения жидкости в открытых призматических руслах с прямым уклоном дна (i > 0):
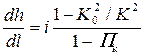 , (4.4.4)
, (4.4.4)
где K0 и K – расходные характеристики, Πk – параметр кинетичности.
• Основное дифференциальное уравнение плавноизменяющегося движения жидкости в открытых призматических руслах с нулевым или обратным уклоном дна (i ≤ 0):
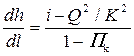 . (4.4.5)
. (4.4.5)
• В случае неравномерного движения воды в открытых руслах кривые свободной поверхности могут приближаться к линии нормальных глубин O – O (если i > 0), или к линии критических глубин K – K, которые для призматического русла остаются неизменными (рис. 4.4.1).
• Если глубина неравномерного движения приближается к нормальной (h → h0), то (K → K0) и в соответствии с уравнением (4.4.4):
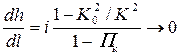 .
.
Это означает, что глубина стремится к постоянной величине, т. е. кривая свободной поверхности асимптотически приближается к линии нормальных глубин.
• Если глубина неравномерного движения приближается к критической (h → hcr), то (Πk→ 1) и в соответствии с уравнением (4.4.4):
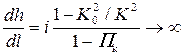 .
.
Кривые свободной поверхности подходят круто, почти под прямым углом к линии критических глубин.
• Если уклон дна равняется критическому ( 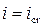 ) при
) при 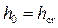 , как это показано на рис. 4.4.1c, то и числитель, и знаменатель выражения (4.4.4) стремятся к нулю. Имеем неопределённость, поскольку кривая свободной поверхности не может подходить асимптотически к линии нормальных глубин и вместе с тем пересекать ее под прямым углом. На практике кривая свободной поверхности асимптотически приближается к линии нормальных глубин.
, как это показано на рис. 4.4.1c, то и числитель, и знаменатель выражения (4.4.4) стремятся к нулю. Имеем неопределённость, поскольку кривая свободной поверхности не может подходить асимптотически к линии нормальных глубин и вместе с тем пересекать ее под прямым углом. На практике кривая свободной поверхности асимптотически приближается к линии нормальных глубин.
• Построение кривых свободной поверхности в открытых руслах. Предварительно следует найти уклон, нормальную и критическую глубину, и, воспользовавшись рис. 4.4.1, установить форму кривой свободной поверхности. Так при i > 0 и 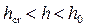 согласно рис. 4.4.1a имеем выпуклую кривую спада, которая от линии нормальных глубин отходит асимптотически, а к линии критических глубин подходит круто. Такая кривая может устанавливаться перед возрастанием уклона дна русла от
согласно рис. 4.4.1a имеем выпуклую кривую спада, которая от линии нормальных глубин отходит асимптотически, а к линии критических глубин подходит круто. Такая кривая может устанавливаться перед возрастанием уклона дна русла от 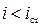 до
до 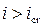 . Если же i = 0 и
. Если же i = 0 и  , то согласно рис. 4.4.1e устанавливается вогнутая кривая подпора, которая начинается от какой-то малой глубины и круто подходит к линии критических глубин. Такая кривая устанавливается при истечении воды из-под щита.
, то согласно рис. 4.4.1e устанавливается вогнутая кривая подпора, которая начинается от какой-то малой глубины и круто подходит к линии критических глубин. Такая кривая устанавливается при истечении воды из-под щита.
• За исходное берут сечение, в котором глубина известна. Таким может быть сечение перед сооружением (плотиной например) или после нее в русле, или сечение, в котором изменяется уклон дна русла. За исходное нельзя брать сечение с нормальной глубиной, поскольку кривая свободной поверхности асимптотически приближается к линии нормальных глубин лишь на бесконечности.
• Итак, прежде всего надо найти критическую и нормальную глубины.
Пример 4.4.1. Рассчитать кривую спада в водоотводной канаве с перепадом, если расход Q = 1,0 м3/с, коэффициент заложения откосов m = 0, ширина русла по дну b = 1 м, уклон дна ступени i = 0,0033, коэффициент шероховатости n = 0,017, нормальная глубина h0 = 0,69 м.
Решение. Находим критическую глубину для прямоугольного сечения 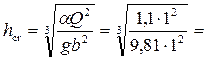 0,48 м. Поскольку
0,48 м. Поскольку 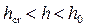 , то согласно рис. 4.4.1a имеем выпуклую кривую спада, которая от линии нормальных глубин отходит асимптотически, а к линии критических глубин подходит круто (рис. 4.4.2).
, то согласно рис. 4.4.1a имеем выпуклую кривую спада, которая от линии нормальных глубин отходит асимптотически, а к линии критических глубин подходит круто (рис. 4.4.2).
Экспериментальные исследования показывают, что критическая глубина hcr устанавливается на некотором расстоянии от стенки перепада. Поэтому за начальную глубину принимаем hb = hcr = 0,48 м, а за конечную he = h0 = 0,69 м. Назначаем расчетные сечения с глубинами h1 = 0,48 м, h2 = 0,52 м, h3 = 0,58 м, h4 = 0,52 м, h5 = 0,69 м.
Выполним расчеты методом Чарномского с использованием табличного процесса MS Excel. Результаты расчётов показаны на рис. 4.4.3.
Для указанных сечений определяем основные гидравлические элементы:
площадь сечения 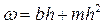 ;
;
смоченный периметр 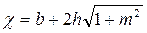 ;
;
гидравлический радиус 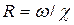 ;
;
показатель степени в формуле скоростной характеристики
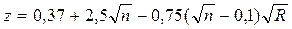 ;
;
расходную характеристику 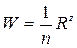 ;
;
удельную энергию сечения 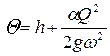 ;
;
уклон трения 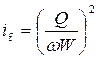 .
.
Среднее значение уклона трения между соседними сечениями 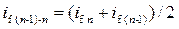 . Расстояние между соседними сечениями
. Расстояние между соседними сечениями
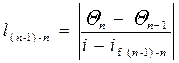 .
.
График, построенный в MS Excel, показан на рис. 4.4.4.
Пример 4.4.2. Построить кривую подпора в канале трапецеидального сечения, перегороженного щитом и истечением из-под щита, если расход Q = 1,0 м3/с; ширина русла по дну b = 0,5 м; коэффициент заложения откосов m = 1,5; коэффициент шероховатости n = 0,025; уклон дна канала i = 0,009; нормальная глубина h0 = 0,52 м; критическая глубина hcr = 0,49 м; уровень воды перед щитом H = 1 м.
Решение. Решение примера методом Чарномского с использованием табличного процессора MS Excel показано на рис. 4.4.5.
Пример 4.4.3. Найти нормальное и критическое наполнение для трубы дождевой канализации диаметром D = 600 мм при расчётном расходе Q = 430 л/с и уклоне земли i = 0,0085.
Решение. Коэффициент шероховатости канализационных труб n = 0,013.
Гидравлический радиус при наполнении доверху
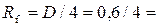 0,15 м,
0,15 м,
площадь живого сечения
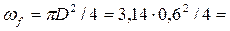 0,283 м2,
0,283 м2,
показатель степени в формуле скоростной характеристики
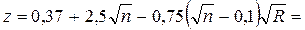
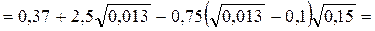 0,65,
0,65,
скоростная характеристика при наполнении доверху
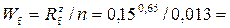 22,4 м/с,
22,4 м/с,
расходная характеристика при наполнении доверху
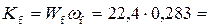 6,33 м3/с,
6,33 м3/с,
относительная расходная характеристика
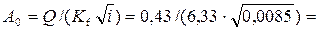 0,737.
0,737.
Из графика “рыбка” (рис. 4.2.2) нормальное наполнение 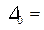 1,40.
1,40.
Расходный параметр
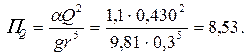
Из графика рис. 4.3.8 находим критическое наполнение
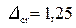 .
.
Критическая глубина
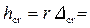 0,3·1,25 = 0,375 м.
0,3·1,25 = 0,375 м.
Расход
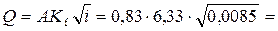 0,484 м3/с.
0,484 м3/с.
Скорость
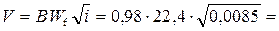 2,02 м/с.
2,02 м/с.
Решение задачи методом Чарномского с использованием табличного процессора MS Excel показано на рис. 4.4.7.
Кривая спада, построенная в MS Excel, показана на рис. 4.4.8.
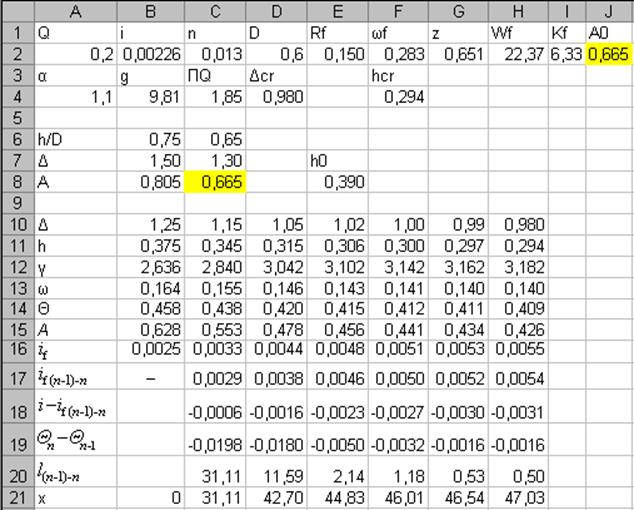 |
| Содержимое ячеек: E2 =D2/4 F2 =СТЕПЕНЬ(E2;G2)/C2 G2 =0,37 2,5*КОРЕНЬ(C2)-0,75*(КОРЕНЬ(C2)-0,1)*КОРЕНЬ(E2) H2 =СТЕПЕНЬ(E2;G2)/C2 I2 =H2*F2 J2 =A2/I2/КОРЕНЬ(B2) C4 =A4*A2*A2/B4/СТЕПЕНЬ(D2/2;5) D4 =ЕСЛИ(C4>2;2-1,038*EXP(-0,0725*C4);0,837*СТЕПЕНЬ(C4;0,257)) F4 =D4*D2/2 B7 =B6*2 B8 =-0,05*СТЕПЕНЬ(B7;4)-0,03746*СТЕПЕНЬ(B7;3) 0,5216*СТЕПЕНЬ(B7;2) 0,00697*B7 E8 =C7*D2/2 H10 =D4 B11 =B10*$D2/2 B12 =2*ACOS(1-2*($D2-B11)/$D2) B13 =(2*ПИ()-B12)*$D2*$D2/8 B14 =B11 $A4*СТЕПЕНЬ($A2/B13;2)/2/$B4 B15 =-0,05*СТЕПЕНЬ(B10;4)-0,03746*СТЕПЕНЬ(B10;3) 0,5216*СТЕПЕНЬ(B10;2) 0,00697*B10 B16 =СТЕПЕНЬ($A2/B15/$I2;2) C17 =(B16 C16)/2 C18 =$B2-C17 C19 =C14-B14 C20 =C19/C18 C21 =B21 C20 |
| Рис. 4.4.7. Решение примера 4.4.3 в MS Excel. |

Рис. 4.4.9. Схема построения кривых свободной поверхности в открытых руслах способом Чарномского.
§
• Гидравлический прыжок – это резкий скачкообразный переход от бурного состояния к спокойному, т.е. переход от глубин, меньших критической, к глубинам, большим критической. Глубины перед прыжком 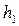 и после него
и после него 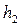 называются взаимными или сопряженными. В зависимости от соотношения взаимных глубин прыжок бывает совершенным (рис. 4.5.1а) или волнистым (рис. 4.5.1б).
называются взаимными или сопряженными. В зависимости от соотношения взаимных глубин прыжок бывает совершенным (рис. 4.5.1а) или волнистым (рис. 4.5.1б).
• Совершенный гидравлический прыжок – это прыжок, в котором над основной транзитной струей образуется участок с водоворотным движением (поверхностный валец).
• В руслах прямоугольного сечения совершенный прыжок образуется, если число Фруда 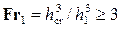 , или если отношение взаимных глубин
, или если отношение взаимных глубин 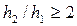 . При этом вторая глубина
. При этом вторая глубина 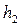 берется на некотором расстоянии от водоворота, в сечении, где заканчивается повышение глубин.
берется на некотором расстоянии от водоворота, в сечении, где заканчивается повышение глубин.
• Импульс жидкости, проходящей за единицу времени через сечение потока,
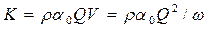 , (4.5.1)
, (4.5.1)
где 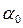 – корректив импульса (коэффициент Буссинеска), учитывающий неравномерность распределения скоростей по сечению (
– корректив импульса (коэффициент Буссинеска), учитывающий неравномерность распределения скоростей по сечению ( 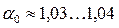 ).
).
• Согласно основному закону динамики изменение импульса жидкости между сечениями 1–1 и 2–2 (рис. 4.5.2) за единицу времени 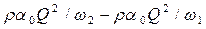 равняется равнодействующей силе, – в данном случае силе гидростатического давления
равняется равнодействующей силе, – в данном случае силе гидростатического давления 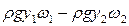 , где y – глубина погружения центра тяжести сечения. Таким образом
, где y – глубина погружения центра тяжести сечения. Таким образом 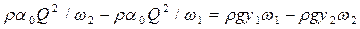 . Отсюда получаем основное уравнение гидравлического прыжка:
. Отсюда получаем основное уравнение гидравлического прыжка:
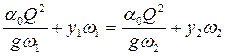 ;
; 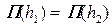 , (4.5.2)
, (4.5.2)
где 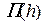 – прыжковая функция:
– прыжковая функция:
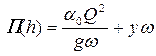 . (4.5.3)
. (4.5.3)
• Прыжковые функции сопряженных глубин равны между собой.
• Приравняв производную прыжковой функции 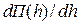 нулю, после ряда преобразований получаем условие минимума прыжковой функции:
нулю, после ряда преобразований получаем условие минимума прыжковой функции:
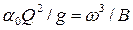 . (4.5.4)
. (4.5.4)
Это уравнение отличается от уравнения (3.2) для определения критической глубины тем, что в одном стоит корректив импульса 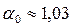 , а в другом корректив кинетической энергии
, а в другом корректив кинетической энергии 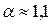 . Поскольку
. Поскольку  , можно считать, что минимум прыжковой функции соответствует минимуму удельной энергии сечения (рис. 4.5.3), т.е. критической глубине.
, можно считать, что минимум прыжковой функции соответствует минимуму удельной энергии сечения (рис. 4.5.3), т.е. критической глубине.
• График рис. 4.5.3 дает возможность объяснить причину резкого увеличения глубин в гидравлическом прыжке. В самом деле, если глубины будут повышаться постепенно, как при плавноизменяющемся движении, то в соответствии с ними постепенно будет изменяться и удельная энергия сечения. Сначала она будет уменьшаться от Θ1 до Θmin, а потом будет увеличиваться от Θmin до Θ1, но это противоречит закону сохранения энергии.
• Для гидравлического прыжка в руслах трапецеидального сечения относительные взаимные глубины 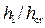 и
и 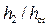 находят по графику Рахманова (рис. 4.5.4) при одинаковых значениях прыжковой функции
находят по графику Рахманова (рис. 4.5.4) при одинаковых значениях прыжковой функции 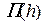 и параметра
и параметра 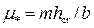 . Приближенно при
. Приближенно при 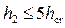 взаимные глубины в руслах трапецеидального сечения можно определить по эмпирическим формулам Рахманова:
взаимные глубины в руслах трапецеидального сечения можно определить по эмпирическим формулам Рахманова:

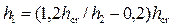 , (4.5.5)
, (4.5.5)
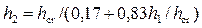 . (4.5.6)
. (4.5.6)
• Для прямоугольного русла
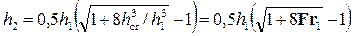 , (4.5.7)
, (4.5.7)
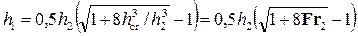 . (4.5.8)
. (4.5.8)
• Относительные взаимные глубины прыжка 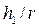 и
и 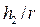 в круглых безнапорных трубах систем водоотведения находят по графику рис. 4.5.5 при одинаковых значениях относительной прыжковой функции
в круглых безнапорных трубах систем водоотведения находят по графику рис. 4.5.5 при одинаковых значениях относительной прыжковой функции  и расходного параметра трубы
и расходного параметра трубы 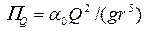 .
.
• Гидравлический прыжок сопровождается потерями энергии, вызванными внутренним трением при вращении жидкости в поверхностном вальце. Если уклон дна незначителен, потери удельной энергии в прыжке (рис. 4.5.3)
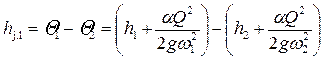 . (4.5.9)
. (4.5.9)
Для русел прямоугольной формы
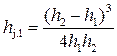 . (4.5.10)
. (4.5.10)
• Чем больше число Фруда 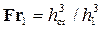 в сечении до прыжка, т.е. чем меньше глубина
в сечении до прыжка, т.е. чем меньше глубина 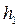 до прыжка, тем большей будет глубина
до прыжка, тем большей будет глубина 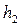 после прыжка и тем большими будут потери энергии в прыжке.
после прыжка и тем большими будут потери энергии в прыжке.
Пример 4.5.1. Определить потери удельной энергии в гидравлическом прыжке трапецеидального сечения, если сопряженные глубины до и после прыжка равны: h1 = 0,4 м, h2 = 0,8 м, а средние в сечениях скорости, соответствующие этим глубинам: V1 = 3,6 м/с и V2 = 1,4 м/с.
Решение. Из уравнения Бернулли потери удельной энергии между сечениями потока
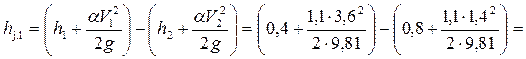 0,217 м.
0,217 м.
• За длину прыжка 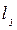 берут расстояние от начала вальца до сечения, где глубины становятся практически постоянными, хотя они и дальше еще немного увеличиваются (рис. 4.5.6). В русле прямоугольного сечения
берут расстояние от начала вальца до сечения, где глубины становятся практически постоянными, хотя они и дальше еще немного увеличиваются (рис. 4.5.6). В русле прямоугольного сечения
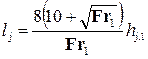 . (4.5.11)
. (4.5.11)
Если Fr1 > 10, можно пользоваться более простой формулой:
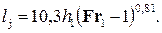 (4.5.12)
(4.5.12)
• Участок потока после прыжка, на котором переформировывается эпюра скоростей, называется послепрыжковым. Для него характерны повышенные пульсации скоростей и давлений, что создает опасность размыва. Длина послепрыжкового участка
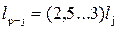 . (4.5.13)
. (4.5.13)
• В руслах прямоугольного сечения волнистый прыжок (рис. 4.5.7) возникает, если 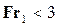 , что соответствует соотношению сопряженных глубин
, что соответствует соотношению сопряженных глубин 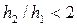 . Поверхностный валец не образовывается, а поток переходит из бурного состояния в спокойное благодаря образованию ряда волн с наибольшей глубиной
. Поверхностный валец не образовывается, а поток переходит из бурного состояния в спокойное благодаря образованию ряда волн с наибольшей глубиной 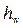 .
.
• Высота первой волны волнистого прыжка
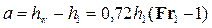 . (4.5.14)
. (4.5.14)
• Отношение сопряженных глубин волнистого прыжка:

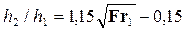 (при
(при 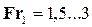 ), (4.5.15)
), (4.5.15)
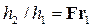 (при
(при  ). (4.5.16)
). (4.5.16)
За бóльшую сопряженную глубину 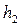 волнистого прыжка принимают глубину в сечении, где волны практически затухают.
волнистого прыжка принимают глубину в сечении, где волны практически затухают.
• Гидравлический прыжок в прямоугольном сечении может использоваться как водомер. Расход
 , (4.5.17)
, (4.5.17)
где 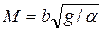 – постоянный множитель для данного русла,
– постоянный множитель для данного русла, 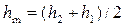 – среднее арифметическое значение взаимных глубин в прыжке.
– среднее арифметическое значение взаимных глубин в прыжке.
Пример 4.5.2. Определить в русле прямоугольного сечения (m = 0) глубину после прыжка h2 и его длину 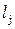 , если расход Q = 1,0 м3/с, ширина русла b = 1 м, а глубина в начале прыжка
, если расход Q = 1,0 м3/с, ширина русла b = 1 м, а глубина в начале прыжка 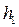 = 0,2 м.
= 0,2 м.
Решение. Критическая глубина
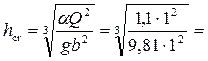 0,482 м/с.
0,482 м/с.
Число Фруда
 14,0.
14,0.
Так как 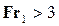 , то прыжок – совершенный.
, то прыжок – совершенный.
Глубина после прыжка
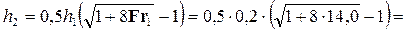 0,964 м.
0,964 м.
Длина прыжка
 16,4 м.
16,4 м.
С использованием графика рис. 4.5.4 имеем
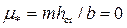 ;
; 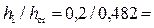 0,415 и
0,415 и 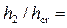 2,0.
2,0.
Глубина после прыжка 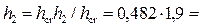 0,92 м.
0,92 м.
Решим ту же задачу с использованием табличного процессора Microsoft Excel (рис. 4.5.8) методом подбора из основного уравнения гидравлического прыжка 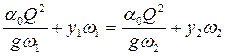 . Для прямоугольного сечения глубина погружения центра тяжести сечения
. Для прямоугольного сечения глубина погружения центра тяжести сечения 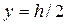 . Равенство
. Равенство 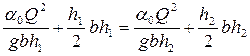 удовлетворяется при
удовлетворяется при 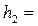 0,93 м.
0,93 м.
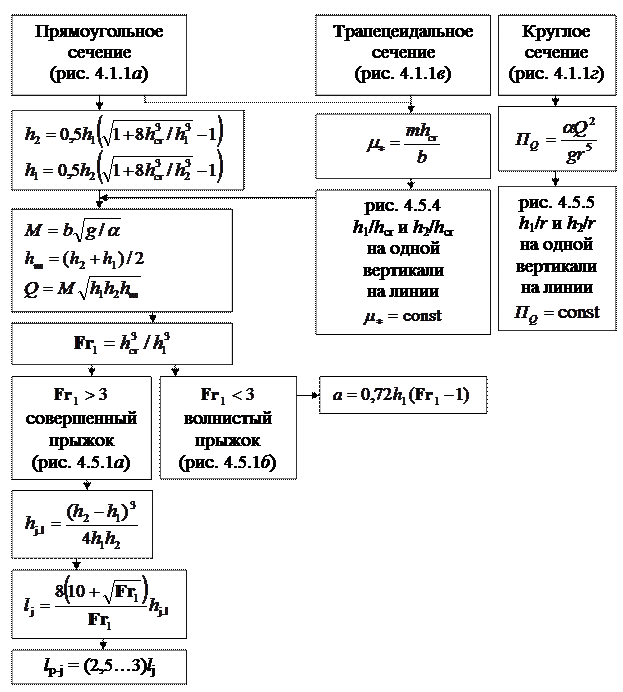
Рис. 4.5.9. Схема расчета гидравлического прыжка.
ТЕМА 4.6. Водосливы
• Водослив – это препятствие в потоке, которое стесняет его снизу и по бокам. Часть потока перед водосливом называется верхним бьефом, часть потока после водослива – нижним бьефом.
• Превышение отметки свободной поверхности в верхнем бьефе над отметкой порога водослива (рис. 4.6.1) называется геометрическим напором на водосливе H. Геометрический напор измеряется на расстоянии (3…4)H от верховой грани водослива, где снижение уровня воды перед водосливом практически несущественно.
• Напор с учетом скорости подхода V0 называется полным напором:
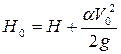 . (4.6.1)
. (4.6.1)
• Разность отметок свободной поверхности жидкости в верхнем и нижнем бьефах называется геометрическим перепадом на водосливе z (рис. 4.6.1). Полным перепадом на водосливе называется сумма геометрического перепада и скоростного напора перед водосливом:
 . (4.6.2)
. (4.6.2)
• В зависимости от толщины δ порога (водосливной стенки) различают водосливы с тонкой стенкой δ < 0,67H (рис. 4.6.2а), с широким порогом (2…3)H < δ < (8…10)H (рис. 4.6.2б), и практического профиля, к которым принадлежат водосливы с промежуточными значениями толщины стенки криволинейного (рис. 4.6.2г) или полигонального (рис. 4.6.2в) очертания.
• Водослив характеризуется также шириной отверстия водослива b, шириной русла, в котором установлен водослив B, высотой водосливной стенки со стороны верхнего бьефа Pu и нижнего бьефа Pd (в случае одинаковых отметок дна до и после водослива эта высота обозначается буквой P).
• Расход через прямоугольный водослив с тонкой стенкой
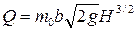 , (4.6.3)
, (4.6.3)
где коэффициент расхода ([H] = м)
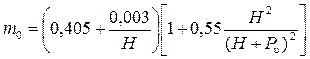 . (4.6.4)
. (4.6.4)
• При протекания воды через прямой водослив с тонкой стенкой без бокового сжатия могут устанавливаться четыре разных типа струи. Свободную струю имеем в случае свободного доступа воздуха под струю (рис. 4.6.3а). При отсутствии доступа воздуха под струю, воздух, который был под ней в начале истечения, постепенно отсасывается, и под струей образуется вакуум, под действием которого высота столба жидкости под струей увеличивается, а струя прижимается к водосливной стенке, превращаясь в прижатую (рис. 4.6.3б). Если при этом выполняется условие H/P ≥ 0,4, то все пространство под струей заполнится водой и теперь она называется подтопленной (рис. 4.6.3в). В случае малых расходов и отсутствия доступа воздуха под струю наблюдается прилипшая струя (рис. 4.6.3г), которая обычно неустойчива и периодически превращается в прижатую.
• Водослив называется затопленным (рис. 4.6.1б), если глубина в нижнем бьефе hd влияет на условия протекания воды через водослив, т.е. на величину расхода Q или напора H.
• Водослив с тонкой стенкой без бокового сжатия затапливается при одновременном выполнении следующих условий:
– отметка воды в нижнем бьефе должны быть выше отметки порога водослива:
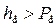 ; (4.6.5)
; (4.6.5)
– относительный перепад на водосливе 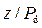 должен быть меньше его критического значения:
должен быть меньше его критического значения:
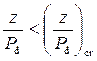 . (4.6.6)
. (4.6.6)
Значение относительного критического перепада выбирают по графику рис. 4.6.4 или по формуле
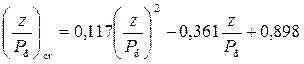 . (4.6.7)
. (4.6.7)
• Расход через затопленный прямоугольный водослив с тонкой стенкой
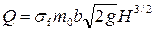 . (4.6.8)
. (4.6.8)
Коэффициент затопления
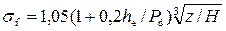 , (4.6.9)
, (4.6.9)
где he – превышение отметки поверхности воды в нижнем бьефе над гребнем водослива, которое называется глубиной подтопления (рис. 4.6.1б):
he = hd – Pd. (4.6.10)
• Формула 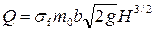 дает возможность использовать прямоугольные водосливы с тонкой стенкой для измерения расхода при напоре H = 0,15…1,25 м. При меньших напорах пользуются треугольным водосливом (рис. 4.6.5) с углом θ = 90°. Расход через такой водослив
дает возможность использовать прямоугольные водосливы с тонкой стенкой для измерения расхода при напоре H = 0,15…1,25 м. При меньших напорах пользуются треугольным водосливом (рис. 4.6.5) с углом θ = 90°. Расход через такой водослив
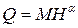 , (4.6.11)
, (4.6.11)
где [Q] = м3/с, [H] = м. Если H = 0,05…0,25 м, то α = 2,5 и M = 1,4. Если H = 0,25…0,5 м, то α = 2,47 и M = 1,343.
Пример 4.6.1. На канале прямоугольного сечения шириной русла b = 2 м установлен водослив с тонкой стенкой высотой P = 1 м. Определить расход Q, если напор на водосливе H = 0,65 м и глубина воды в нижнем бьефе hd = 1,2 м (рис. 4.6.1б).
Решение. Отношение напора на водосливе к его высоте H/P = 0,65/1 = 0,65. Перепад на водосливе 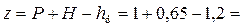 0,45 м. Относительный перепад на водосливе
0,45 м. Относительный перепад на водосливе  0,45. По графику рис. 4.6.4 критический перепад (z/P)cr ≈ 0,75. Так как уровень воды в нижнем бьефе расположен выше порога водослива:
0,45. По графику рис. 4.6.4 критический перепад (z/P)cr ≈ 0,75. Так как уровень воды в нижнем бьефе расположен выше порога водослива: 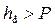 (1,2 > 1) и относительный перепад на водосливе z/P меньше его критического значения: z/P < (z/P)cr (0,45 < 0,75), то водослив затоплен. Коэффициент расхода
(1,2 > 1) и относительный перепад на водосливе z/P меньше его критического значения: z/P < (z/P)cr (0,45 < 0,75), то водослив затоплен. Коэффициент расхода
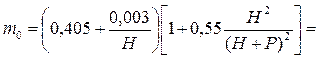
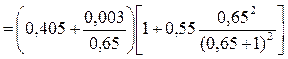 = 0,444.
= 0,444.
Глубина подтопления he = hd – P = 1,2 – 1 = 0,2 м.
Коэффициент затопления
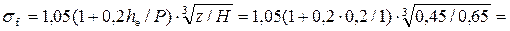 0,966.
0,966.
Расход воды 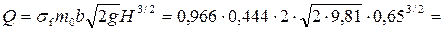 2,0 м3/с.
2,0 м3/с.
Пример 4.6.2. В канале установлен треугольный водослив с тонкой стенкой с углом при вершине θ = 90° (рис. 4.6.5). Напор на пороге водослива H = 0,5 м. Определить расход Q воды в канале.
Решение. Если H = 0,25…0,5 м, то α = 2,47 и M = 1,343.
Расход  = 0,242 м3/с.
= 0,242 м3/с.
• Водосливы практического профиля криволинейного очертания могут быть безвакуумными и вакуумными. Безвакуумные водосливы имеют очертание (рис. 4.6.6а), совпадающее с нижней поверхностью струи, которая переливается через водослив с тонкой стенкой (очертание Кригера-Офицерова).
Если водосливная поверхность не доходит до струи (рис. 4.6.6б), то под струей устанавливается давление, меньшее атмосферного, а водослив называется вакуумным. Струя прижимается к водосливу. Один и тот же водослив может быть как вакуумным, так и безвакуумным. В самом деле, при увеличении напора на безвакуумном водосливе струя старается откинуться дальше от водослива и между ним и водосливной поверхностью образуется вакуум.
• Пропускная способность водосливов практического профиля
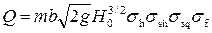 . (4.6.12)
. (4.6.12)
• Коэффициент расхода безвакуумного водослива m = 0,49…0,5. Вакуумные водосливы имеют большую пропускную способность, поскольку скорость потока на водосливе увеличивается в случае уменьшения давления. Коэффициент расхода вакуумного водослива может достигать значений m = 0,54…0,57.
• Коэффициент полноты напора σh учитывает отличие напора H на водосливе от расчетного напора Hc, по которому построено очертание водослива Кригера-Офицерова. Если H/Hc = 0,2…1, то σh = 0,84…1; если H/Hc = 1…2 (это уже вакуумный профиль), то σh = 1…1,1; если H = Hc, то σh = 1.
• Коэффициент формы σsh зависит от близости формы оголовка к очертанию Кригера-Офицерова). Обычно σsh = 0,85…1.
• Коэффициент бокового сжатия
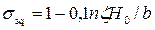 , (4.6.13)
, (4.6.13)
где ζ – коэффициент формы береговых опор и промежуточных быков (рис. 4.6.7); n – количество боковых сжатий, при одном отверстии водослива n = 2, при двух отверстиях n = 4 и т.д.
• Коэффициент затопления σf находят по графику рис. 4.6.8 в зависимости от отношения he/H0 (см. рис. 4.6.1б). Кривая 1 принадлежит вакуумным водосливам (рис. 4.6.6б), кривая 2 – безвакуумным водосливам (рис. 4.6.6а), кривая 3 – водосливам с расширенным гребнем (рис. 4.6.9).
• Незатопленный водослив с широким порогом. В зависимости от ширины порога могут устанавливаться такие схемы протекания потока.
• При δ ≈ (2…4)H глубина потока непрерывно понижается на пороге (рис. 4.6.10б).
• При (2…4)H < δ < (8…10)H на пороге устанавливается параллельноструйное движение с глубиной h < hcr (рис. 4.6.10а).
• При δ > (8…10)H на условия протекания потока начинают влиять силы трения, т.е. пропускная способность водослива становится зависимой от потерь энергии по длине, и водослив можно рассматривать как короткий канал. В начале порога устанавливается так называемая сжатая (т.е. наименьшая) глубина hsq и ряд волн, которые затухают с переходом через критическую глубину, которая соответствует минимальной удельной энергии сечения Θ и обозначена на рис. 4.6.11 линией К–К. Такой переход называется волнистым гидравлическим прыжком.
• Пропускная способность незатопленных водосливов с широким порогом
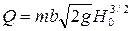 . (4.6.14)
. (4.6.14)
• Коэффициент расхода для водосливов с широким порогом 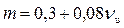 , где νu – параметр сжатия потока при входе на водослив, который равняется отношению произведения ширины отверстия b водослива на величину напора H перед водосливом к площади живого сечения Ωu в верхнем бьефе:
, где νu – параметр сжатия потока при входе на водослив, который равняется отношению произведения ширины отверстия b водослива на величину напора H перед водосливом к площади живого сечения Ωu в верхнем бьефе:
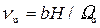 . (4.6.15)
. (4.6.15)
Для неплавных оголовков прямоугольных подводящих русел 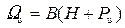 , где B – ширина подводящего русла, Pu – высота водослива со стороны верхнего бьефа.
, где B – ширина подводящего русла, Pu – высота водослива со стороны верхнего бьефа.
• Для нахождения глубины h на пороге водослива с широким порогом используют уравнение Бернулли для сечений, проходящих через точки A перед водосливом и C на его пороге, относительно плоскости сравнения, проведенной через верховую грань водослива (рис. 4.6.10а):
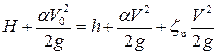 , (4.6.16)
, (4.6.16)
где 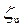 – коэффициент сопротивления на входе на водослив, V – скорость на пороге водослива. С учетом формул
– коэффициент сопротивления на входе на водослив, V – скорость на пороге водослива. С учетом формул 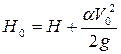 ,
, 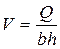 ,
, 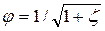 , а также считая, что α ≈ 1, получаем:
, а также считая, что α ≈ 1, получаем:
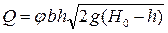 , (4.6.17)
, (4.6.17)
где коэффициент скорости 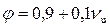 . Отсюда
. Отсюда
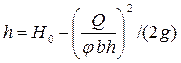 . (4.6.18)
. (4.6.18)
• Затопленный водослив с широким порогом (рис. 4.6.12). Затопление происходит, если глубина подтопления (превышение отметки поверхности воды в нижнем бьефе над гребнем водослива) he > NH, где критерий затопления N ≈ 0,8.
• Параметр сжатия потока при выходе из водослива
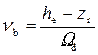 , (4.6.19)
, (4.6.19)
где 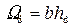 – площадь живого сечения в нижнем бьефе.
– площадь живого сечения в нижнем бьефе.
• Характер течения на затопленном водосливе зависит от условий входа на него. Если вход плавный и степень подтопления значительная, на водосливе устанавливается приблизительно горизонтальная поверхность с перепадом восстановления zr на выходе в нижний бьеф (рис. 4.6.12а). При неплавном входе на пороге образуется впадина с последующим волнистым повышением глубины (рис. 4.6.12б). Пропускная способность затопленного водослива
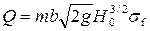 , (4.6.20)
, (4.6.20)
где коэффициент затопления σf = 0,44…1 в зависимости от степени затопления he/H и условий на входе (плавный или неплавный вход).
• Энергия сечения на выходе из водослива вследствие потерь напора на сопротивлении водослива ниже энергии на входе, что при спокойном состоянии потока (рис. 4.3.1) означает уменьшение глубины в нижнем бьефе по сравнению с глубиной в верхнем бьефе на величину z.
• В случае большой степени затопления (he/H ≥ 0,95) для определения пропускной способности лучше пользоваться формулой:
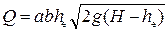 . (4.6.21)
. (4.6.21)
Значения поправочного коэффициента a = 0,8…2,4 в зависимости от параметра сжатия потока при выходе из водослива νb и условий на входе и выходе (плавные они или нет) представлены в табл. 4.6.1.
Таблица 4.6.1. Поправочный коэффициент в формуле расхода через водослив.
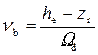 | a при входе и выходе | |
| неплавных | плавных | |
| 0,1 0,3 0,5 0,7 | 0,8 1,35 | 0,9 1,1 1,6 2,4 |
• Расчет отверстий водопропускных сооружений. Отверстия шлюзов-регуляторов, малых мостов и т.п. не имеют порога, и напор перед ними образуется за счет бокового сжатия русла (рис. 4.6.13).
• Водомерные лотки. На очистных сооружениях (рис. 4.6.14) систем водоотвода (канализации) измерение расхода сточных вод необходимо для регулирования и контроля над работой очистных сооружений. Применение для этих целей мерных водосливов с тонкой стенкой невозможно, поскольку сточные воды будут создавать заиливание перед водосливом. Поэтому для измерения расхода сточных вод обычно применяют водомерные лотки, работающие по схеме водослива без порога (P = 0), что исключает заиливание (рис. 4.6.15). Для уменьшения потерь энергии лотки выполняют с постепенным плавным сужением к горловине и расширением после нее.

Рис. 4.6.14. Очистные сооружения.
• На рис. 4.6.15а показан лоток, работающий в условиях затопленного истечения (лоток Вентури). Расход через такой лоток (из уравнения Бернулли):
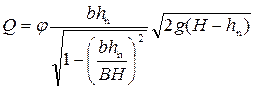 , (4.6.22)
, (4.6.22)
где φ – коэффициент скорости (при плавном входе φ = 0,96…0,97, при неплавном входе φ = 0,90…0,95), 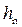 – высота воды в сжатом сечении лотка, b – ширина суженной части лотка, H – глубина в канале перед входом в лоток, B – ширина канала.
– высота воды в сжатом сечении лотка, b – ширина суженной части лотка, H – глубина в канале перед входом в лоток, B – ширина канала.
• Если суженная вставка выполнена со значительным (i > icr) уклоном (рис. 4.6.15б), то в горловине лотка поток становится бурным, возникает гидравлический прыжок через критическую глубину и вода через лоток протекает по схеме незатопленного (свободного) водослива. В этом случае расход
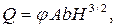 (4.6.23)
(4.6.23)
где; A – коэффициент, зависящий от отношения 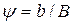 :
:
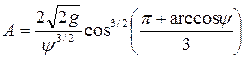 . (4.6.24)
. (4.6.24)
Условие установления критической глубины в лотке:
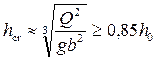 , (4.6.25)
, (4.6.25)
где 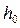 – глубина воды при равномерном движении в канале, в котором установлен лоток.
– глубина воды при равномерном движении в канале, в котором установлен лоток.
Пример 4.6.3. В канале прямоугольного сечения шириной 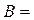 1 м и с уклоном дна
1 м и с уклоном дна 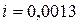 установлен для измерения проходящего расхода воды лоток с критической глубиной (рис. 4.6.15б). Стенки и дно канала облицованы кирпичом (
установлен для измерения проходящего расхода воды лоток с критической глубиной (рис. 4.6.15б). Стенки и дно канала облицованы кирпичом ( 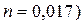 ; высота боковых стенок канала
; высота боковых стенок канала 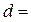 1,3 м. Максимальный расход воды в канале
1,3 м. Максимальный расход воды в канале 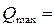 1 м3/с. Требуется определить ширину горловины лотка b для обеспечения условий свободного истечения.
1 м3/с. Требуется определить ширину горловины лотка b для обеспечения условий свободного истечения.
Решение. Определяем глубину воды при равномерном движении в канале в условиях максимального расхода  . Задаёмся различными значениями глубин до тех пор, пока не устанавливаем, что максимальному расходу
. Задаёмся различными значениями глубин до тех пор, пока не устанавливаем, что максимальному расходу 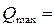 1 м3/с соответствует глубина
1 м3/с соответствует глубина 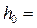 1 м. Действительно, в этом случае:
1 м. Действительно, в этом случае:
площадь живого сечения  1 м2;
1 м2;
смоченный периметр 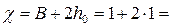 3 м;
3 м;
гидравлический радиус 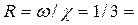 0,333 м;
0,333 м;
показатель степени в формуле скоростной характеристики
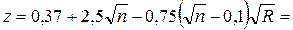
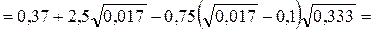 0,683;
0,683;
скоростная характеристика 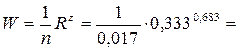 27,8 м/с;
27,8 м/с;
расходная характеристика 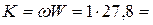 27,8 м3/с;
27,8 м3/с;
расход 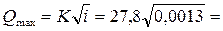 1 м3/с.
1 м3/с.
Исходя из условия (4.6.26), минимальное значение критической глубины
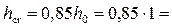 0,85 м.
0,85 м.
Из (4.6.25) необходимая для создания такой критической глубины ширина горловины лотка
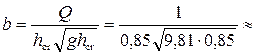 0,44 м.
0,44 м.
Принимаем  0,4 м;
0,4 м; 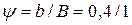 = 0,4.
= 0,4.
Коэффициент
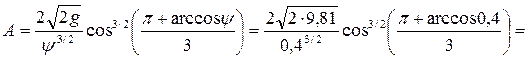 1,77.
1,77.
Принимаем значение коэффициента 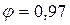 .
.
Из (4.6.24) глубина в верхнем бьефе 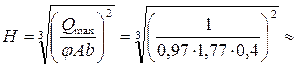 1,28 м.
1,28 м.
Эта глубина в верхнем бьефе является допустимой для подходного участка канала, так как 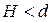 (1,28 < 1,3 м).
(1,28 < 1,3 м).
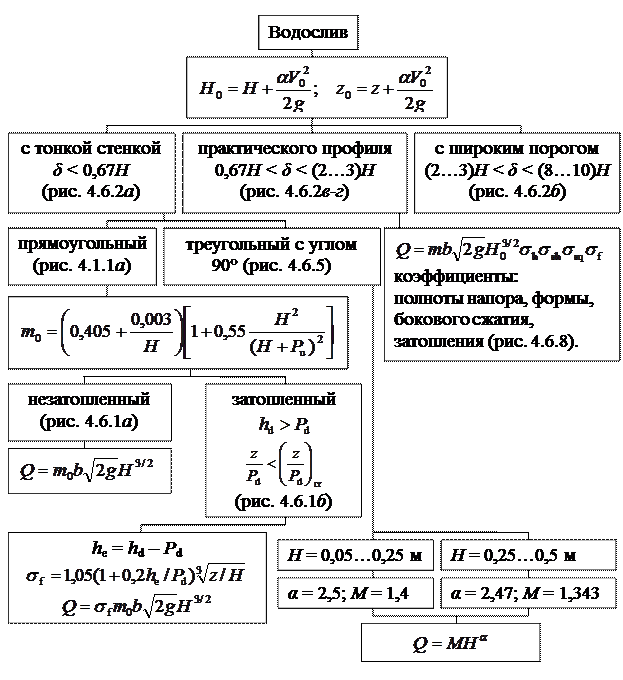 Рис. 4.6.16. Схема расчета водосливов.
Рис. 4.6.16. Схема расчета водосливов.
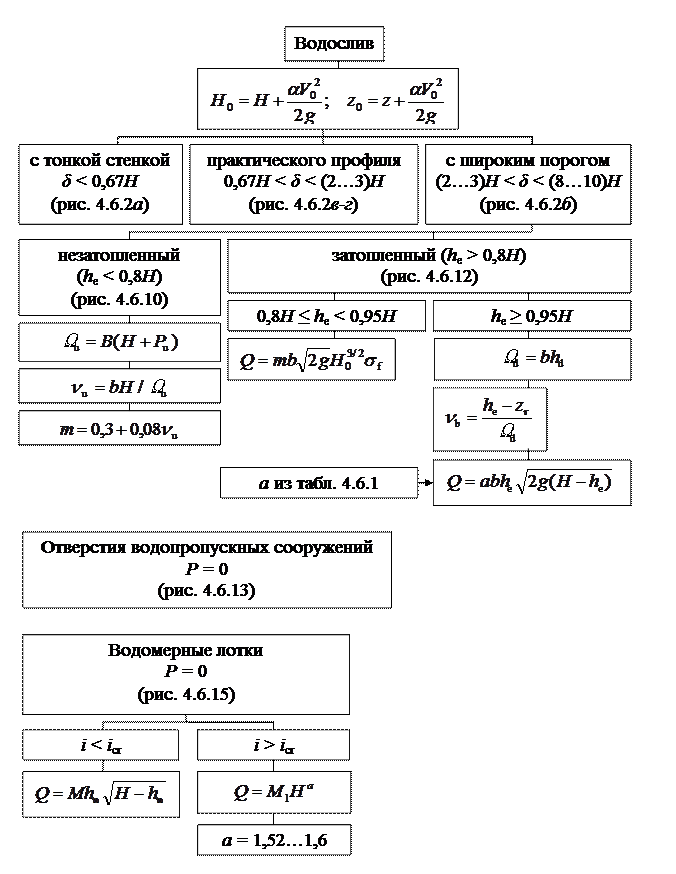 Рис. 4.6.17. Схема расчета водосливов (продолжение).
Рис. 4.6.17. Схема расчета водосливов (продолжение).
ТЕМА 4.7. Сопряжение бьефов
• При протекании воды через водослив скорость потока возрастает и достигает максимального значения непосредственно за водосливом в так называемом сжатом сечении C–C, где устанавливается наименьшая глубина hsq (рис. 4.7.1). После сжатого сечения уклон дна уменьшается, и скорость постепенно уменьшается, а глубина увеличивается.
• Уравнение Бернулли для сечений O–O и C–C относительно плоскости сравнения 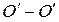 , проведенной на отметке дна нижнего бьефа:
, проведенной на отметке дна нижнего бьефа:
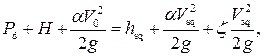 (4.7.1)
(4.7.1)
где Pd – высота водослива относительно дна нижнего бьефа; V0 – скорость подхода потока к водосливу; hsq, Vsq – соответственно глубина и скорость в сжатом сечении; ζ – коэффициент сопротивления на водосливе. Левая часть уравнения – это удельная энергия потока в верхнем бьефе относительно дна нижнего бьефа:
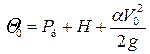 . (4.7.2)
. (4.7.2)
С учетом того, что 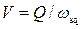 (где
(где 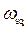 – площадь сжатого сечения) и обозначив
– площадь сжатого сечения) и обозначив 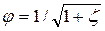 (φ – коэффициент скорости), получим уравнение, из которого методом подбора можно найти глубину hsq:
(φ – коэффициент скорости), получим уравнение, из которого методом подбора можно найти глубину hsq:
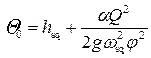 . (4.7.3)
. (4.7.3)
• Значение коэффициента скорости φ для криволинейных водосливов практического профиля берем из графика рис. 4.7.2.
• Для компьютерных расчётов показанную на графике рис. 4.7.2 зависимость можно представить в виде:
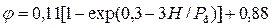 . (4.7.4)
. (4.7.4)
• Для русел прямоугольного сечения ωsq = bhsq, и глубина в сжатом сечении
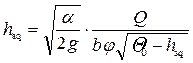 . (4.7.5)
. (4.7.5)
Из построенного по этой формуле графика (рис. 4.7.3) можно определить относительную глубину в сжатом сечении ξsq = hsq/hcr и сопряжённую с ней относительную глубину 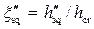 в зависимости от ξΘ0 = Θ0/hcr и коэффициента скорости φ.
в зависимости от ξΘ0 = Θ0/hcr и коэффициента скорости φ.
• Формы сопряжения бьефов. Уклон дна нижнего бьефа обычно меньше уклона низовой грани водослива. Поэтому средняя скорость потока после сжатого сечения уменьшается, а глубина увеличивается.
• Если уклон дна в нижнем бьефе больше критического (i > icr), то состояние потока в нем бурное (рис. 4.7.4), и после водослива устанавливается без гидравлического прыжка через критическую глубину кривая подпора по типу нижней кривой на рис. 4.4.1б.
• Если уклон дна нижнего бьефа меньше критического (i < icr) и состояние потока в отводном русле спокойное, глубина увеличивается согласно форме кривой подпора (нижняя кривая на рис. 4.4.1а), а дальше наблюдается гидравлический прыжок к глубинам, больше критической (рис. 4.7.5).
• Бытовая глубина hn в отводном русле – это глубина, которая установилась бы в данном сечении в случае отсутствия водослива. В частном случае при равномерном движении в отводном русле бытовая глубина равняется нормальной глубине h0.
§
• Движение грунтовых вод является частным случаем фильтрации – движения жидкости в пористой среде.
• Фильтрация происходит через поры грунта и может быть ограничена снизу и сверху водонепроницаемыми (водоупорными) слоями грунта. Такая фильтрация называется напорной (рис. 4.8.1).
• Если водоупорный слой ограничивает поток только снизу, то такая фильтрация называется безнапорной (рис. 4.8.2). Поверхность безнапорного фильтрационного потока называется депрессивной, а кривая свободной поверхности – кривой депрессии. В зависимости от расхода депрессивная поверхность занимает разные положения.
• Безнапорное движение грунтовых вод чаще является неравномерным, поскольку гидравлический уклон J, как правило, не равняется уклону водоупорного слоя i (см. рис. 4.8.2).
• Отношение расхода Q ко всей площади фильтрационного потока ω называется скоростью фильтрации:
V = Q/ω. (4.8.1)
• В мелкозернистых грунтах (пески, глина, суглинки и т.п.) происходит ламинарная фильтрация, которая характеризуется потерями напора, прямо пропорциональными скорости фильтрации в первой степени.
• В крупнозернистых песках и материалах (гравий, галька, щебень, камень) происходит турбулентная фильтрация, при которой потери напора пропорциональны скорости в степени выше, чем первой.
• При фильтрации вода проходит через поры между частичками грунта. Отношение площади пор в сечении фильтрационного потока ωp ко всей площади сечения ω называется коэффициентом пористости грунта: p = ωp/ω. Его значение обычно находится в пределах p = 0,3…0,5.
• Основной закон фильтрации:
Q = kωJm, (4.8.2)
где k – коэффициент фильтрации (см. табл. 4.8.1), зависящий от рода грунта и температуры воды; J – гидравлический уклон, который является потерей напора на единице длины фильтрационного потока:
J = hl/l. (4.8.3)
m – показатель степени, для ламинарной фильтрации m = 1, для турбулентной – m = 0,5…1.
Таблица 4.8.1. Коэффициент фильтрации.
| Грунты | k, см/с |
| Глина Суглинок Супесь Песок: мелкозернистый среднезернистый крупнозернистый Галька и гравий | 1·10-7 1·10-7…1·10-5 1·10-5…1·10-3 1·10-4…1·10-3 1·10-3…1·10-2 1·10-2…1·10-1 1·10-1…1·10 |
• С учетом (6.2) скорость фильтрации
V = kJm. (4.8.4)
• При ламинарной фильтрации скорости фильтрации малы (V ~ 1 мм/с). В расчетах скоростным напором αV2/(2g) пренебрегают и считают, что полный напор равняется пьезометрическому (H0 = H), а гидравлический уклон пьезометрическому (J = ip).
• Прибор Дарси (рис. 4.8.3) представляет собой цилиндр с дырчатым дном и выведенными из боковой поверхности цилиндра пьезометрами. Цилиндр заполняют исследуемым грунтом. Установившееся движение воды через прибор обеспечивается поддержанием постоянной отметки поверхности воды в приборе благодаря сбросу излишка воды в сбросную трубу. Коэффициент ламинарной фильтрации
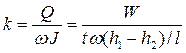 , (4.8.5)
, (4.8.5)
где W – объем воды, проходящей через прибор за время t,  – площадь сечения цилиндра.
– площадь сечения цилиндра.
• Равномерное безнапорное движение грунтовых вод. Гидравлический и пьезометрический уклоны равны уклону водоупорного слоя i (рис. 4.8.4):
J = ip = i. (4.8.6)
И тогда расход
Q = ωki, (4.8.7)
глубина равномерного движения
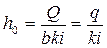 , (4.8.8)
, (4.8.8)
где ω = bh0 – площадь сечения потока, q = Q/b – расход на единицу ширины потока.
• Неравномерное безнапорное движение грунтовых вод. В этом случае (рис. 4.8.5) уклон кривой депрессии
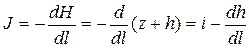 , (4.8.9)
, (4.8.9)
где H – пьезометрический напор над плоскостью сравнения 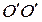 , z – отметка водоупорного слоя, h – глубина фильтрационного потока,
, z – отметка водоупорного слоя, h – глубина фильтрационного потока, 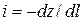 – уклон водоупорного слоя. Тогда расход
– уклон водоупорного слоя. Тогда расход
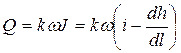 . (4.8.10)
. (4.8.10)
Расход на единицу ширины потока (удельный расход)
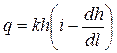 . (4.8.11)
. (4.8.11)
Получено дифференциальное уравнение неравномерного плавноизменяющегося движения грунтовых вод.
• Интегрируя дифференциальное уравнение (4.8.11), получаем расстояние 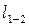 между сечениями с глубинами
между сечениями с глубинами 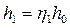 и
и 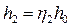 :
:
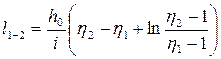 . (4.8.12)
. (4.8.12)
• На практике часто бывает, что уклон водоупорного слоя i = 0. Тогда уравнение (4.8.11) приобретает вид:
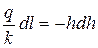 . (4.8.13)
. (4.8.13)
Интегрированием уравнения (4.8.13) получаем уравнение Дюпюи:
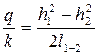 . (4.8.14)
. (4.8.14)
• Дренаж – это система подземных каналов (дрен), через которые осуществляется осушение сельскохозяйственных земель, отвод от сооружений грунтовых вод и снижение их уровня. Воду из дренажной сети выводят за границы осушаемой территории.
• Приток воды к галерее, расположенной на водоупорном слое (рис. 4.8.6). Согласно уравнению Дюпюи (4.8.14), удельный приток воды с одной стороны дренажной галереи (рис. 4.8.6)
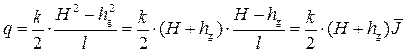 , (4.8.15)
, (4.8.15)
где q – удельный приток с одной стороны галереи, l – длина влияния галереи (расстояние от галереи, на котором уровень грунтовых вод практически не снижается), H – толщина водоносного слоя, 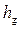 – глубина воды в галерее,
– глубина воды в галерее, 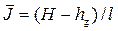 – средний уклон кривой депрессии, значение которого в зависимости от вида грунта приведены в табл. 4.8.2.
– средний уклон кривой депрессии, значение которого в зависимости от вида грунта приведены в табл. 4.8.2.
Таблица 4.8.2. Средний уклон кривой депрессии.
| Вид грунта | 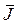 |
| Плотные глины Глинистые грунты Песчано-глинистые грунты Песок Крупный песок, галька | 0,15 0,1 0,05…0,1 0,005…0,015 0,003…0,005 |
• Подставляя найденное значение q в уравнение Дюпюи
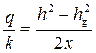 , (4.8.16)
, (4.8.16)
находят глубину воды h на расстоянии x от галереи и строят кривую депрессии.
• Приток воды к галерее, размещенной выше водоупорного слоя (рис. 4.8.7). Такая галерея называется висячей. Удельный приток
q = 2(qlat qbot), (4.8.17)
где удельный приток через одну боковую стенку
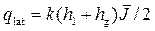 . (4.8.18)
. (4.8.18)
Чтобы найти удельный приток qbot через половину ширины дна, вычисляем значения коэффициентов 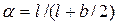 ,
, 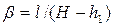 . Потом из графика рис. 4.8.8 находим относительную величину
. Потом из графика рис. 4.8.8 находим относительную величину 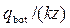 и, в конце концов, вычисляем
и, в конце концов, вычисляем 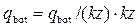 . Кривую депрессии можно построить по уравнению (4.8.16) с учетом того, что в этом случае q = qlat.
. Кривую депрессии можно построить по уравнению (4.8.16) с учетом того, что в этом случае q = qlat.
• Приток воды к круглому совершенному дренажному колодцу. Совершенным называется колодец, расположенный на водоупорном слое (рис. 4.8.9). При откачивании воды из колодца глубина в нем будет уменьшаться, но из-за разности уровней грунтовых вод и отметки воды в колодце вода со всех сторон будет притекать к нему по радиальным направлениям. Основной закон фильтрации (4.8.2) принимает вид:
 . (4.8.19)
. (4.8.19)
Отсюда дифференциальное уравнение кривой свободной поверхности:
 . (4.8.20)
. (4.8.20)
Интегрируя это уравнение, получаем уравнение кривой депрессии для совершенного колодца:
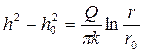 . (4.8.21)
. (4.8.21)
Приток воды к колодцу или необходимая величина откачки
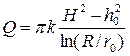 , (4.8.22)
, (4.8.22)
где H – толщина водоносного слоя. Радиус влияния колодца R определяют по эмпирической формуле Зихарда:  , где глубина откачки
, где глубина откачки 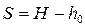 , [R] = м, k – коэффициент фильтрации, м/с.
, [R] = м, k – коэффициент фильтрации, м/с.
Пример 4.8.1. Определить дебит совершенного дренажного колодца, если отметка статического уровня грунтовых вод H = 15 м, отметка уровня воды в колодце h0 = 10 м, отметка водоупорного слоя 0,00 м, диаметр колодца d = 40 см, радиус влияния колодца R = 150 м, коэффициент фильтрации k = 0,03 см/с.
Решение. Радиус колодца r0 = d/2 = 0,2 м. Дебит совершенного дренажного колодца 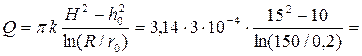 0,0177 м3/с.
0,0177 м3/с.
• Приток воды к совершенному артезианскому колодцу. Артезианский колодец забирает воду из водоносного слоя, ограниченного сверху и снизу водоупорными грунтами (рис. 4.8.10). Вода в таком слое находится под давлением и называется артезианской. В этом случае статический напор (за пределами радиуса влияния колодца) и напор в любом сечении h отличаются от толщины водоносного слоя a. Дебит колодца
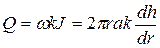 , (4.8.23)
, (4.8.23)
откуда
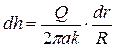 . (4.8.24)
. (4.8.24)
Интегрируя полученное дифференциальное уравнение, имеем:
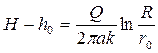 . (4.825)
. (4.825)
Отсюда дебит артезианского колодца
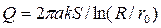 , (4.8.26)
, (4.8.26)
где 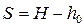 – глубина откачки.
– глубина откачки.
Пример 4.8.2. Найти дебит совершенного артезианского колодца диаметром d = 25 см, забирающего воду из водоносного песчаного слоя толщиной a = 8 м, если коэффициент фильтрации k = 0,002 см/с, напор в водоносном слое в естественном состоянии H = 20 м, глубина воды в колодце h0 = 10 м.
Решение. Радиус колодца r0 = d/2 = 0,125 м,
глубина откачки 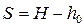 = 10 м,
= 10 м,
радиус влияния колодца  134,2 м,
134,2 м,
дебит колодца
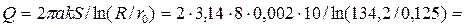 0,00144 м3/с.
0,00144 м3/с.
• Совершенный поглощающий круглый колодец. Такой колодец служит для сброса поверхностной воды, которая фильтруется в водоносный слой (рис. 4.8.11). Кривая депрессии в этом случае имеет форму, обратную к кривой депрессии дренажного колодца (рис. 4.8.9). Поглощающая способность поглощающего колодца
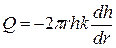 . (4.8.27)
. (4.8.27)
Эта формула отличается от (4.8.19) только знаком “–”, который показывает, что в этом случае вода движется от колодца, а не к нему. После интегрирования получим:
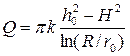 . (4.8.28)
. (4.8.28)
• Фильтрация воды через земляные плотины.
На рис 4.8.12 показана Асуанская земляная плотина.
• Рассмотрим однородную (из однородного грунта, т.е. с постоянным коэффициентом фильтрации k) земляную плотину на водоупорном основании (рис. 4.8.13). Сила давления воды в водохранилище направлена по нормали к верховому откосу плотины, поэтому фильтрационный поток входит в тело плотины под прямым углом, а потом его линии течения на участке AB приобретают вогнутый характер. На дальнейшем пути BC кривая депрессии имеет форму, подобную кривой притока к дренажной галерее (см. рис. 4.8.6). После точки C часть фильтрационного потока выходит за промежуток высачивания CD, а часть – на затопленный откос DE. Расчет фильтрации основывается на разделении фильтрационного потока на три клина.
• Верховой клин ограничен верховым откосом плотины и вертикальной плоскостью, проходящей через точку B, размещенную на одной вертикали с бровкой плотины. Для верхового клина
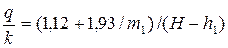 , (4.8.29)
, (4.8.29)
где 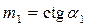 – коэффициент заложения верхового откоса, H и h1 – напоры в начале и в конце верхового клина.
– коэффициент заложения верхового откоса, H и h1 – напоры в начале и в конце верхового клина.
• Средний клин соответствует участку BC, движение на котором описывается уравнением Дюпюи:
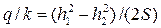 , (4.8.30)
, (4.8.30)
где S – длина среднего клина, т.е. расстояние между живыми сечениями фильтрационного потока, проведенными через точки B и C:
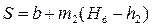 , (4.8.31)
, (4.8.31)
где b – ширина плотины по верху, Hd – высота плотины,  – коэффициент заложения откоса низовой грани, h2 – глубина в сечении, проходящем через точку C.
– коэффициент заложения откоса низовой грани, h2 – глубина в сечении, проходящем через точку C.
• Низовой клин соответствует участку CE. Для низового клина
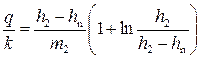 . (4.8.32)
. (4.8.32)
• Через все три клина проходит один и тот же расход q, поэтому решая задачу о фильтрации через плотину, имеем четыре неизвестных величины: q, h1, h2, S, которые можно определить, решив систему из четырех уравнений: (4.8.29), (4.8.30), (4.8.31), (4.8.32).
Пример 4.8.3. Определить фильтрационный расход на 1 м длины плотины и построить кривую депрессии при отсутствии воды в нижнем бьефе (hn = 0), если Hd = 14 м, H = 12 м, b = 10 м, m1 = 3, m2 = 2, k = 0,4 м/сут (рис. 4.8.14).
Решение. Используем систему уравнений (4.8.29), (4.8.30), (4.8.31), (4.8.32) при hn = 0 и известных Hd, H, b, m, m2. Тогда получим:
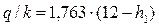 ;
;
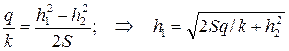 ;
;
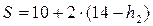 ;
;
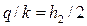 .
.
Назначаем несколько значений h2 и выполняем расчеты, результаты которых заносим в табл. 4.8.3. По результатам расчетов строим линии а и б зависимости 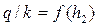 (рис. 4.8.15).
(рис. 4.8.15).
Таблица 4.8.3. Расчёт параметров фильтрации через плотину.
| h2, м | 3,0 | 3,5 | 4,0 |
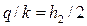 , м; линия а на рис. 4.8.14 , м; линия а на рис. 4.8.14 | 1,50 | 1,75 | 2,00 |
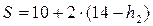 , м , м | |||
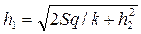 , м , м | 10,25 | 10,99 | 11,66 |
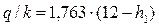 , м; линия б на рис. 4.8.14 , м; линия б на рис. 4.8.14 | 3,09 | 1,78 | 0,60 |
Из графика рис. 4.8.15 получаем:
h2 = 3,53 м, q/k = 1,76 м.
Тогда q = (q/k)·k = 1,76∙0,4 = 0,704 м2/сут.
Расстояние 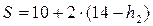 = 30,94 м.
= 30,94 м.
Кривую депрессии на участке среднего клина (рис. 4.8.14) строим согласно уравнению (4.8.30) для значений l = 0…S. Результаты расчетов приведены в табл. 4.8.4.
Таблица 4.8.4. Расчёт кривой депрессии.
| l, м | 30,94 | ||||||
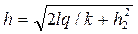 , м , м | 3,53 | 5,48 | 6,90 | 8,01 | 9,10 | 10,02 | 11,02 |
• Фильтрация через земляную плотину с ядром. Для уменьшения фильтрации через земляную плотину, в ней устраивается ядро из малопроницаемого грунта, например, глины (рис. 4.8.16а). Фильтрационный поток в ядре заменяют эквивалентным потоком в прямоугольном массиве грунта, из которого изготовлена плотина, шириной 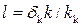 , где k и kk – коэффициенты фильтрации грунта соответственно тела плотины и ядра, δk – средняя толщина ядра. Итак, расчет фильтрации через земляную плотину с ядром сводится к расчету плотины из однородного грунта с теми же коэффициентами заложения откосов, но с большей шириной по верху, которая называется приведенной (рис. 4.8.16б):
, где k и kk – коэффициенты фильтрации грунта соответственно тела плотины и ядра, δk – средняя толщина ядра. Итак, расчет фильтрации через земляную плотину с ядром сводится к расчету плотины из однородного грунта с теми же коэффициентами заложения откосов, но с большей шириной по верху, которая называется приведенной (рис. 4.8.16б):
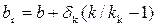 . (4.8.33)
. (4.8.33)

Рис. 4.8.17. Схема к расчёту фильтрации.
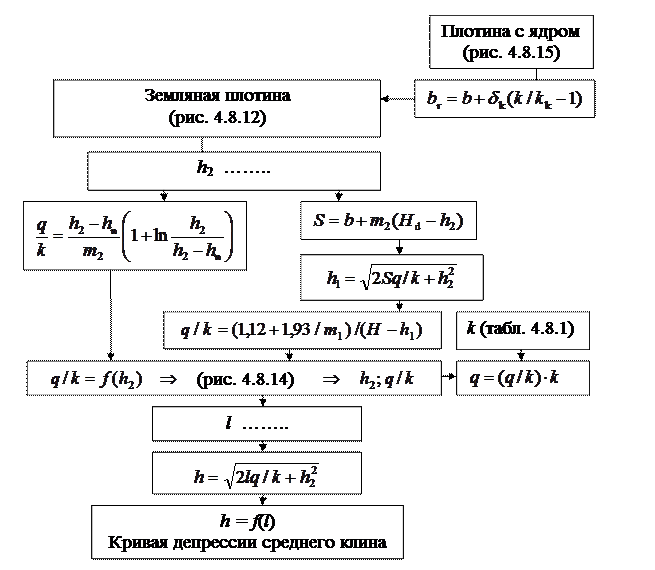
Рис. 4.8.18. Схема к расчёту фильтрации сквозь земляную плотину.
§
• Сложные гидротехнические сооружения не подлежат точному расчету и при проектировании нужно проводить исследование на моделях для качественной и количественной оценки явления. На модели воссоздают то же самое явление, что и в натуре, но в другом масштабе. На рис. 4.9.1 показаны гидравлическое моделирование прохождения судна по каналу (а) и моделирование волнения в гавани (б).
• Геометрическое подобие выражается в следующих отношениях длин, площадей и объемов в натуре и на модели:
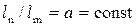 ; (4.9.1)
; (4.9.1)
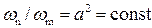 ; (4.9.2)
; (4.9.2)
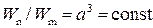 , (4.9.3)
, (4.9.3)
где a – линейный масштаб.
• Кинематическое подобие означает, что при установившемся движении отношение скоростей течения в подобных точках натуры и модели будет постоянным:
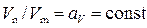 , (4.9.4)
, (4.9.4)
где aV – масштаб скоростей.
Поскольку время 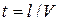 , то
, то
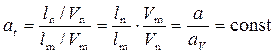 . (4.9.5)
. (4.9.5)
Ускорение при равноускоренном движении 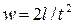 , поэтому масштаб ускорений
, поэтому масштаб ускорений
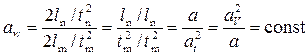 . (4.9.6)
. (4.9.6)
• Динамическое подобие означает, что масштаб сил постоянен для всех точек:
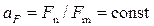 . (4.9.7)
. (4.9.7)
Поскольку сила  , то масштаб сил
, то масштаб сил
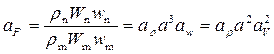 , (4.9.8)
, (4.9.8)
где 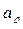 – масштаб плотностей.
– масштаб плотностей.
Это выражение называется законом подобия Ньютона в масштабных множителях.
Таким образом
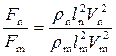 , (4.9.9)
, (4.9.9)
или
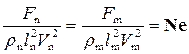 . (4.9.10)
. (4.9.10)
Критерий 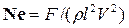 называется критерием Ньютона. Его можно выразить еще и в таком виде:
называется критерием Ньютона. Его можно выразить еще и в таком виде:
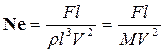 , (4.9.11)
, (4.9.11)
где 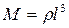 – масса жидкости в рассматриваемом объеме.
– масса жидкости в рассматриваемом объеме.
Для любых подобных точек в натуре и на модели критерии Ньютона должны быть одинаковыми.
• В гидравлических явлениях одновременно действуют силы тяготения, давления, трения, инерции и т.п. Для всех сил одновременное выполнение условия (4.9.10) невозможно, но этого можно достичь, когда некоторые из действующих сил имеют преобладающее значение по сравнению с другими.
• При движении жидкости в напорном трубопроводе важнейшую роль играют силы трения. Потеря напора на трение по длине трубы в соответствии с обобщенной формулой Дарси-Вейсбаха 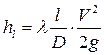 есть работа силы трения, приходящаяся на единицу веса жидкости. Таким образом, сила трения
есть работа силы трения, приходящаяся на единицу веса жидкости. Таким образом, сила трения
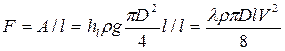 . (4.9.12)
. (4.9.12)
Подставляя это выражение в обе части (4.9.10), находим:
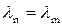 , (4.9.13)
, (4.9.13)
т. е. потоки жидкости в трубопроводах будут гидравлически подобными, если гидравлические коэффициенты трения λ в натуре и на модели будут равны между собой.
• При ламинарном режиме течения или при турбулентном режиме в диапазоне гидравлически гладких труб гидравлический коэффициент трения, – λ = 64/Re (формула Пуазейля) и 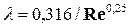 (формулу Блазиуса), – зависит только от числа Рейнольдса Re = VD/ν. Итак, в этом случае потоки будут подобными, если для схожих точек натуры и модели числа Рейнольдса будут одинаковыми. Обычно на модели используют ту же жидкость, что и в натуре (воду). Поэтому из равенства чисел Рейнольдса следует:
(формулу Блазиуса), – зависит только от числа Рейнольдса Re = VD/ν. Итак, в этом случае потоки будут подобными, если для схожих точек натуры и модели числа Рейнольдса будут одинаковыми. Обычно на модели используют ту же жидкость, что и в натуре (воду). Поэтому из равенства чисел Рейнольдса следует:
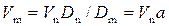 , (4.9.14)
, (4.9.14)
т.е. при моделировании по критерию Рейнольдса скорость на модели должна быть в a раз большей, чем на натуре.
• В квадратичном диапазоне сопротивления турбулентного режима движения коэффициент трения λ не зависит от числа Рейнольдса Re. Поэтому на модели число Rem может быть меньше, чем Ren, но не меньше допустимого значения
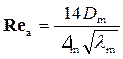 , (4.9.15)
, (4.9.15)
где Δm – высота выступов шероховатости на модели.
При Rem ≥ Rea этот диапазон называется автомодельным. При работе в автомодельном диапазоне скорость на модели
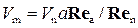 . (4.9.16)
. (4.9.16)
Пример 4.9.1. В натурных условиях в напорном трубопроводе (рис. 4.9.2) диаметром Dn = 150 мм протекает вода (кинематическая вязкость νn = 0,01 см2/с) с расходом Qn = 30 л/с. Определить предельный расход воды на модели стального трубопровода диаметром Dm = 32 мм с эквивалентной шероховатостью Δm = 0,05 мм в условиях гидродинамического подобия.
Решение. Скорость в натурных условиях
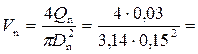 1,7 м/с.
1,7 м/с.
Число Рейнольдса 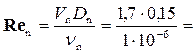 255000.
255000.
Гидравлический коэффициент трения на модели в автомодельной области
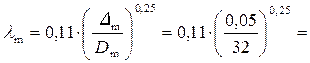 0,0219.
0,0219.
Линейный масштаб: 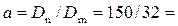 4,69.
4,69.
Минимальное допустимое число Рейнольдса:
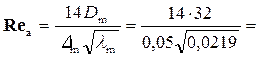 60600.
60600.
Скорость на модели 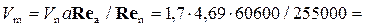 1,9 м/с.
1,9 м/с.
Расход потока на модели
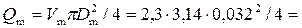 1,52·10-3 м3/с = 1,52 л/с.
1,52·10-3 м3/с = 1,52 л/с.
• При анализе гидравлического прыжка, протекания воды через водосливы и другие сооружения преобладающей является сила веса выделенной массы жидкости 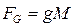 . В этом случае равенство критериев Ньютона (4.9.11) принимает вид:
. В этом случае равенство критериев Ньютона (4.9.11) принимает вид:
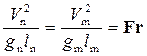 . (4.9.17)
. (4.9.17)
Число 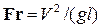 (отношение удвоенной удельной кинетической энергии к глубине) носит название критерия Фруда.
(отношение удвоенной удельной кинетической энергии к глубине) носит название критерия Фруда.
Поскольку gn = gm, то из (4.9.18) масштаб скоростей
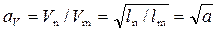 , (4.9.18)
, (4.9.18)
а масштаб расходов
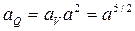 . (4.9.19)
. (4.9.19)
Пример 4.9.2. Модель водослива (рис. 4.9.3) изготовлена размером в 1/25 натуры (линейный масштаб a = 25), измеренные скорость и расход равны: Vm = 0,5 м/с и Qm = 1,5 л/с. Найти соответствующие скорость и расход в натуре.
Решение. Преобладающей является сила веса. По критерию Фруда 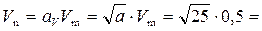 2,5 м/с;
2,5 м/с;
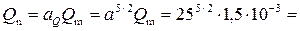 4,69 м3/с.
4,69 м3/с.
Пример 4.9.3. Определить напор Hn перед щитом, открытие an и ширину bn щитового отверстия в натуре (рис. 4.7.15) для пропуска потока с расходом Qn = 3 м3/с, если на модели с шириной отверстия bm = 20 см при расходе Qm = 9 л/с открытие щита am = 3 см.
Решение. По Фруду
масштаб расхода aQ = Qn/Qm = 3/0,009 = 333,3;
линейный масштаб 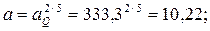
ширина щитового отверстия в натуре bn = abm = 10,22∙0,2 = 2,04 м;
открытие щитового отверстия в натуре an = aam = 10,22∙0,03 = 0,307 м.
Из формулы пропускной способности щитового отверстия (4.7.11)
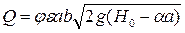 ,
,
приняв в первом приближении коэффициент вертикального сжатия ε = 0,65 и коэффициент скорости φ = 0,95, находим полный напор перед щитом в натуре

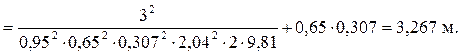
Геометрический напор перед щитом в натуре
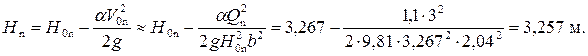
Уточняем коэффициент вертикального сжатия. По таблице рис. 4.7.13 при an/Hn = 0,307/3,257 = 0,094 коэффициент вертикального сжатия ε = 0,614.
Тогда полный напор в натуре


Геометрический напор перед щитом в натуре
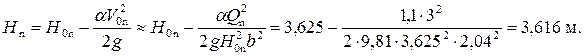
an/Hn = 0,307/3,616 = 0,085 и коэффициент вертикального сжатия ε = 0,617.
Поскольку ε практически не изменилось, расчёт закончен и окончательно имеем: an = 0,307 м; bn = 2,04 м; Hn = 3,616 м.
• Моделирование равномерных течений в открытых неразмываемых руслах. При моделировании равномерных потоков в открытых неразмываемых руслах необходимо в модели создать тот же уклон, что и в натуре, а шероховатость модели и её масштаб подобрать таким образом, чтобы число Фруда в модели было равно числу Фруда в натуре Fr = 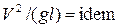 . Моделирование выполняется в автомодельной области. Для этого линейный масштаб не должен превышать значения
. Моделирование выполняется в автомодельной области. Для этого линейный масштаб не должен превышать значения
 . (4.9.20)
. (4.9.20)
Пример 4.9.4. Определить максимальное уменьшение размеров потока, скорость и расход на бетонной модели канала прямоугольного сечения (коэффициент откоса m = 0) с шириной дну bn = 10 м, глубиной h0n = 1 м и расходом Qn = 5 м3/с. Коэффициент шероховатости бетонированных стенок и дна канала nn = 0,014. Работа канала должна быть проверена на модели. Требуется рассчитать модель.
Решение. Определяем характеристики потока в натурных условиях:
площадь сечения 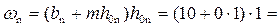 10 м2;
10 м2;
смоченный периметр 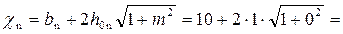 12 м;
12 м;
гидравлический радиус Rn = ωn/χn = 10/12 = 0,83 м;
средняя скорость Vn = Qn/ωn = 5/10 = 0,5 м/с.
В качестве материала модели выбираем бетон с эквивалентной шероховатостью Δeq m = 0,6 мм и коэффициентом шероховатости n = 0,014.
Предварительно берём линейный масштаб α = 10.
Определяем характеристики потока в модели в первом приближении:
гидравлический радиус Rm = Rn/a = 0,83/10 = 0,083 м;
скоростная характеристика 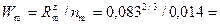 13,6 м/с;
13,6 м/с;
гидравлический коэффициент трения

Максимальный возможный масштаб моделирования
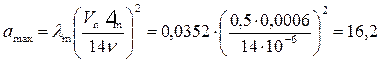 .
.
Берём это значение для масштаба моделирования во втором приближении и снова находим значения Rm, Wm, λm, amax. Далее следует третье приближение и т. д., пока очередное значение amax практически сравняется с a.
Расчёт в MS Excel показан на рис. 4.9.4. В третьем приближении было достигнуто значение amax = 20,02.
Окончательно берём линейный масштаб α = 20.
Определяем характеристики потока в модели:
глубина воды hm = h0n/α = 1/20 = 0,05 м;
ширина по дну bm = bn/α = 10/20 = 0,5 м;
средняя скорость 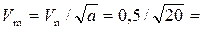 0,11 м/с;
0,11 м/с;
площадь сечения ωm = ωn/a2 = 10/202 = 0,025 м2;
расход Qm = Vmωm = 0,11∙0,025 = 0,00280 м3/с = 2,80 л/с.
Пример 4.9.5. Требуется определить в модели подпор воды в реке Δhn, вызываемый устройством моста. Длина мостовой опоры ln = 24 м; ширина её bn = 4,3 м; глубина воды в русле (до устройства моста) hn = 8,2 м; средняя скорость течения воды Vn = 2,3 м/с; расхода воды в реке Qn = 1650 м3/с.
Решение. Выбираем масштаб модели (по условиям лаборатории) a = 50. Находим линейные размеры модели:
длина опоры lm = ln/a = 24/50 = 0,48 м;
ширина bm = bn/a = 4,3/50 = 0,083 м.
Определяем глубину потока в модели: hm = hn/a = 8,2/50 = 0,164 м.
По Фруду средняя скорость в модели 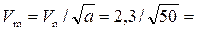 0,325 м,
0,325 м,
расход 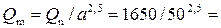 0,0928 м3/с.
0,0928 м3/с.
Проведённые в модели опыты показали, что подпор Δhm = 0,018 м.
В натуре подпор будет: Δhn = a∙Δhm = 50∙0,018 = 0,9 м.
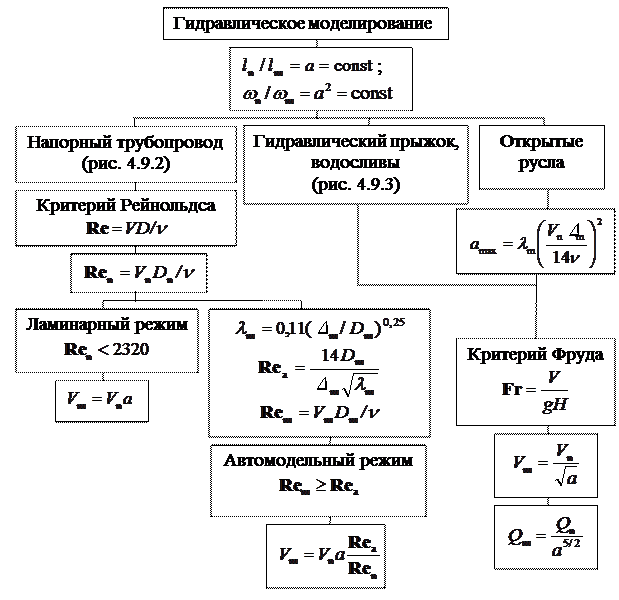 Рис. 4.9.5. Схема к расчёту параметров гидравлического моделирования.
Рис. 4.9.5. Схема к расчёту параметров гидравлического моделирования.
РАЗДЕЛ 5. ГИДРОЛОГИЯ
§
Географическая карта Донецкой области показана на рис. 5.2.1. Уровень воды Азовского моря − 0,4 м, поэтому прибрежная зона лежит ниже уровня мирового океана. На рис. 5.2.1. показана карта Донецкой области с нанесенными на неё реками и городами. Донецкая область находится в степной зоне, климат умеренно континентальный, с малоснежной зимой и жарким летом. Средние температуры января от −5 до −8°C, июля 21–23°С. Осадков около 500 мм в год. Весной бывают суховеи (чаще – в мае), летом – засухи, иногда – пыльные бури, град, зимой – метели.
Самое высокое место области — безымянная высота 336 м, расположенная вблизи железнодорожных остановочных пунктов Платформа № 3 и Метеорологический в Дебальцево; самое низкое место (− 0,4 м) — уровень воды в Азовском море. Рельеф преимущественно равнинный (высотой до 200 м), расчленённый оврагами и балками. На северо-востоке находится Донецкий кряж высотой до 366 м, поверхность которого изрезана долинами рек. На западе кряж переходит в Приднепровскую низменность, на юге – в Приазовскую низменность с отдельными поднятиями (Могила-Гончариха, Саур-Могила и другие). На юге – узкая полоса Причерноморской низменности, которая уступами обрывается к Азовскому морю. В местах залегания известняков и соленосных отложений развиваются карстовые формы рельефа. Характерная черта рельефа области – наличие форм антропогенного происхождения: терриконы, карьеры и т. д.
По территории Донецкой области протекают около 110 рек, из которых 47 длиной более 25 км. Общая длина рек составляет более чем 3000 км. Самая крупная из них – Северский Донец длиной 1053 км, а в границах области – более 100 км, шириной от 60 до 80 м. Средняя глубина 1,5–2 м (на плёсах достигает 7 м). Её притоки – Казённый Торец, Бахмутка и Лугань.
Все реки области принадлежат к 3-м бассейнам: Азовского моря, Дона и Днепра. К бассейну Днепра относятся реки: Самара и Волчья; к бассейну Азовского моря: Кальмиус, Грузский Еланчик, Крынка.
Реки — равнинного типа, преимущественно снежного и дождевого питания. Многие реки летом пересыхают и водоснабжение осуществляется за счёт 20 водохранилищ (наибольшие — Кураховское, Старокрымское, Карловское, Клебан-Быкское, Верхнекальмиусское и другие). На рис. 5.2.3 видим Нижнекальмиусское водохранилище. Сооружены 1011 прудов общей площадью водного зеркала 8049 га.
Озёр на территории области мало, есть небольшие озёра в пойме Северского Донца (Волчье и другие), а также Славянские солёные озёра — Слепное и Репное (рис. 5.2.4).

Рис. 5.2.3. Нижнекальмиусское водохранилище в черте Донецка.

Рис. 5.2.4. Солёное озеро Репное в Славянске.
Основные глубины залегания подземных вод создаваемых от сточных, дождевых и талых вод находятся в пределах 8-12 м. Данная вода «верховодка» скапливается на первом водоупоре (глина) и в своем хим. составе содержит превышающие дозы нитратов, пестицидов и солей тяжелых солей. Чаще всего – это уровень выкопанных колодцев и мелких скважин.
Наиболее распространенный водоносный горизонт Донецкой области – меловой. Глубина залегания не менее 40 м. Усредненное расположение при проведении геологоразведки 70 – 200 м.
Юрский горизонт часто используется для бурения артезианских скважин. Глубина залегания составляет от 160 до 380 м. Артезианские скважины юрского горизонта часто используются для водообеспечения питьевой водой города и села.
Донбасс находится на юрском и каменноугольном щите. Вода в Донбассе чаще всего находится в трещиноватых породах (водопроницаемые горные породы). Вода добытая из недр земли, содержит повышенное содержание минеральных солей (0,7 – 4 г/л). В соответствии с гигиеническими требованиями к качеству питьевой воды суммарная минерализация не должна превышать величины 1 г/л.
Северные районы Донецкой области бурят глубокие артезианские скважины на юрский горизонт. Дебет этих скважин около 1,0 – 1,5 м.куб/мин. Вода содержится в водопроницаемых породах: пеках, трещиноватых известняках, прослойках песчаников и глин.
Донбасс испытывает хронический водный голод. Между тем, почти под всем засушливым Донбассом протянулась уникальная система сбора грунтовой влаги. Образовали ее старые выработки угольных шахт, общий лабиринт которых достигает нескольких тысяч километров. Эта колоссальная дренажная система собирает ежегодно 770-800 млн кубометров воды, которой теоретически хватило бы для удовлетворения нужд всего востока страны. Например, в Луганской области, согласно официальной статистике, из шахт отводят 228 млн кубометров воды в год, что заметно превышает традиционный водозабор из артезианских скважин и крупнейшей реки региона Северского Донца. Проблема же заключается в том, что так называемые шахтные воды обильно загрязнены природными и техногенными веществами. Даже если в шахтерском городе закрывается последняя шахта, администрация должна заботиться об откачке воды из заброшенных выработок. Иначе шахтные воды поднимутся к поверхности, отравят плодородный слой земли, подтопят дома, дороги, коммунальные сети.
Несколько лет назад Европейский Союз предложил Украине профинансировать разработку проекта использования шахтных вод для бытовых нужд. Самые современные технологии очистки позволяют снизить себестоимость полученной питьевой воды до 0,01 или даже 0,001 копейки за литр. К тому же ученые рекомендовали одновременно с водоочисткой сооружать цех по добычи из отходов (рапы — концентрированного солевого раствора) дефицитных химических веществ, что заметно приближало проект к отметке самоокупаемости. Однако средств на строительство установки у государства не нашлось.
ТЕМА 5.3. Река
Бассейн реки – часть земной поверхности, включая толщу почвогрунтов, с которой происходит сток в отдельную речку или речную систему. На рис. 5.3.1 показан бассейн реки Северский Донец.

Рис. 5.3.1. Бассейн реки Северский Донец.
Бассейн каждой реки включает в себя поверхностный и подземный водосборы.
Поверхностный водосбор ограничен водораздельной линией a (рис. 5.3.2), проходящей по наиболее высоким точкам земной поверхности. Положение этой линии определяется по картам.
Подземный водосбор ограничен водораздельными линиями водоупорных подземных напластований b (рис. 5.3.2). Определение подземного водосбора затруднительно и обычно ограничиваются только поверхностным.
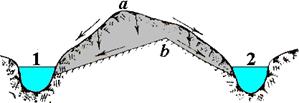
Рис. 5.3.2. Водораздельные линии поверхностного (а) и подземного (б) водосборов.
По величине поверхностного водосбора F различают:
Большие реки F > 50.000 км2;
Средние реки 2.000 км2 < F < 50.000 км2;
Малые реки F < 2.000 км2.
Водораздел – граница между двумя бассейнами, проходящая по наивысшим точкам местности.
Длина рекиL – это расстояние от истока до устья, измеренное не по береговой линии, а по геометрической оси реки. Так как реки кочуют, их длина различна в различные сроки. Например, длина Днепра в 1800 г. составляла 2050 км, в 1950 г. – 2201 км, а сейчас – 2285 км.
Извилистость реки характеризуется коэффициентом извилистости 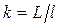 , где l – кратчайшее расстояние от истока до устья.
, где l – кратчайшее расстояние от истока до устья.
Речная (гидрографическая) сеть бассейна – это совокупность всех рек, балок, водотоков, впадающих в главную реку. Главной рекой обычно считается та, у которой наибольший расход и наибольшая длина.
Средняя ширина бассейна реки 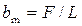 , где F – площадь водосбора, L – длина реки.
, где F – площадь водосбора, L – длина реки.
Гидрологический режим некоторых рек указан в табл. 5.3.1.
Густота речной сети характеризуется коэффициентом 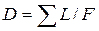 , где
, где 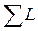 – суммарная длина всех рек и балок, F – площадь водосбора.
– суммарная длина всех рек и балок, F – площадь водосбора.
Коэффициент D изменяется от 0 до 1,3 и зависит от высоты расположения бассейна над уровнем моря, от почвогрунтов, облесённости и т. д. Чем выше бассейн, тем больше осадков, и тем гуще сеть. Так у Днепра D изменяется от 0,211 в верховьях до 0,125 в низовье.
Долины – это относительно узкие, вытянутые в длину, извилистые, наклонённые в одном направлении углубления земной поверхности. Часть дна долины, занятая водным потоком, называется руслом. Речные долины не пересекаются, а сливаясь вместе, образуют общую сеть.
Ширина и глубина долины зависит главным образом от твердости слагающих пород.
Долины горных рек имею форму ущелий. На рис. 5.3.3 показано Дарьяльское ущелье.
Если долина расположена в мягких размываемых породах, то она быстро расширяется. Вначале берега становятся наклонными, а дно остаётся узким. Постепенно долина приобретает трапецеидальную форму с широким дном и пологими склонами. При дальнейшем размыве долина принимает корытообразную форму. На рис. 5.3.4 показана долина реки Апста в Абхазии.
Таблица 5.3.1. Гидрологический режим некоторых рек.
| река (бассейн) | Площадь водосбора F, тыс. км2 | Годовой сток, W, км3 в год | Длина L, км |
| Большие реки Волга (Каспийское море) Днепр (Чёрное море) Дон (Азовское море) Северский Донец (Дон) Средние реки Волчья (Самара – Днепр) Айдар (Северский Донец) Кальмиус (Азовское море) Крынка (Миус – Азовское море) Малые реки Грузская (Кальмиус) | > 50 | 5,6 | |
Форма долин зачастую усложнена террасами или горизонтальными площадками на склонах (рис. 5.3.5). Затопляемая во время половодья нижняя терраса называется поймой. Участки долин, затопляемые высокими водами, называются поймами.
В горных породах долины приобретают вид узких глубоких каньонов, а пойменные участки отсутствуют.
Основными характеристиками русла является его ширина, глубина, площадь водного сечения.
При половодье на равнинных реках потоки воды в русле и пойме могут расслаиваться и двигаться не параллельно.
Речное русло в плане обычно имеет извилистую форму и состоит из ряда излучин, или меандр (рис. 5.3.6). Даже незначительное препятствие, отклоняющее течение к одному из легко размываемых берегов, может вызвать образование целой серии излучин. Постепенно увеличивается вогнутость подмываемого берега. Продукты размыва уносятся водой и откладываются ниже по течению. На рис. 5.3.7 показана излучина Амазонки.
В некоторых местах концы излучин сближаются, и река прорывает перешеек. Скорость в новом русле возрастает. Вход в излучину перекрывается наносами, старое русло отмирает и превращается в староречье. Староречьем является озеро Банное в Святогорске (рис. 5.3.8).

Рис. 5.3.3. Дарьяльское ущелье.

Рис. 5.3.4. Корытообразная долина реки.
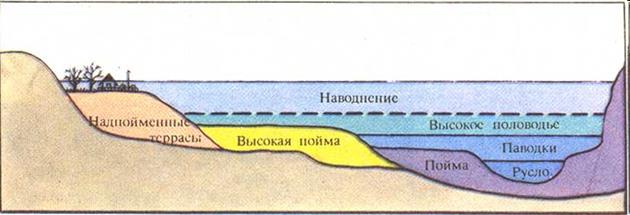
Рис. 5.3.5. Долина реки, усложнённая террасами.

Рис. 5.3.6. Излучины (меандры) русла реки.

Рис. 5.3.7. Излучина Амазонки.

Рис. 5.3.8. Староречье Северского Донца озеро Банное в Святогорске.
Извилистость реки образуется в результате следующих причин:
– Турбулентность движения потока.
– Наличие притока со стороны.
– Наличие кориолисова ускорения (инерционного ускорения, возникающего в неинерциальной системе отсчёта, связанной с Землёй).
Глубина воды по длине реки не одинакова. Глубокие участки, называемые плёсами, чередуются с мелкими участками – перекатами (рис. 5.3.9). Плёсы характерны для излучин, а переката находятся на переходах от одной излучины к другой.
Линии равных глубин называются изобатами. Линия максимальных глубин и максимальных скоростей называется стрежнем (фарватером).
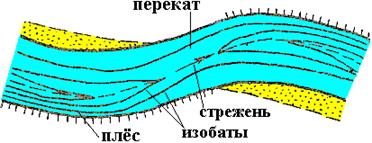
Рис. 5.3.9. Плёсы чередуются с перекатами.
Уклон участка реки 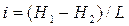 , где
, где 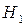 и
и 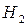 – отметки уровней воды в начале и в конце участка, L – длина участка реки по геометрической оси, проходящей посредине реки. Уклоны равнинных рек составляют 0,001–0,0001, а у горных рек достигает 0,01 и более. В верховьях рек уклоны больше, чем в низовьях.
– отметки уровней воды в начале и в конце участка, L – длина участка реки по геометрической оси, проходящей посредине реки. Уклоны равнинных рек составляют 0,001–0,0001, а у горных рек достигает 0,01 и более. В верховьях рек уклоны больше, чем в низовьях.
Средневзвешенный уклон определяется по средневыравненному уклону продольного профиля реки (рис. 5.3.10). ABCD – продольный профиль русла. Линия АЕ проведена так, что положительные и отрицательные площади, отсекаемые ею, равны между собой. Средневзвешенный уклон реки 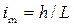 . На рис. 5.3.11 приведен график гидрологических показателей Днестра.
. На рис. 5.3.11 приведен график гидрологических показателей Днестра.
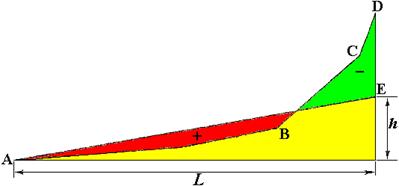
Рис. 5.3.10. Средневзвешенный уклон.
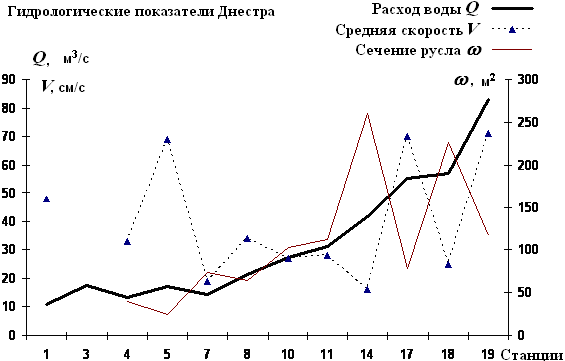
Рис. 5.3.11. График гидрологических показателей Днестра.
Река имеет не только продольный, но и поперечный уклон. Поперечный уклон обусловливается тем, что центробежная сила на закруглениях русла прижимает воду к вогнутому берегу, а это приводит к повышению уровня по сравнению с выпуклым берегом. Кроме того, под действием силы Кориолиса движущаяся масса воды отклоняется в северном полушарии вправо, подмывая правый берег. На рис. 5.3.12 виден крутой правый берег Северского Донца в Святогорске. В южном полушарии под действием силы Кориолиса подмывается левый берег.

Рис. 5.3.12. Крутой правый берег Северского Донца в Святогорске.
Уровень воды может повышаться у одного берега и понижаться у другого, если ветер дует поперек русла или под некоторым углом к направлению потока. У наветренного берега уровень воды повышается, а у противоположного понижается (рис. 5.3.13).

Рис. 5.3.13. Повышение уровня воды у наветренного берега.
ТЕМА 5.4. Факторы стока
Характеристики речного стока:
Расход водыQ – объём воды, прошедший за единицу времени через поперечное сечение реки, [Q] = м3/с.
Объем стокаW – объём воды, прошедший через сечение реки за определенный промежуток времени.
Слой осадковX – объём осадков объём осадков (precipitation) Wp, выпавших за определенный промежуток времени, отнесенный к площади водосбора: X = Wp/F; [X] = мм.
Слой стокаY – объём воды, прошедший через поперечное сечение реки за определенный промежуток времени, отнесенный к площади водосбора: Y = W/F; [Y] = мм.
Модуль стокаМ – объём воды, прошедший через поперечное сечение за единицу времени, отнесенный к площади водосбора: M = Q/F; [M] = л/с/км2.
Коэффициент стока h – отношение высоты слоя стока к высоте слоя выпавших в бассейн реки осадков: η = Y/X.
Модульный коэффициент – отношение модуля стока (или расхода) данного года к среднемноголетнему значению (норме этой величины).
Соотношения между характеристиками стока:
Годовой слой стока в мм
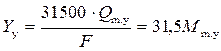 , где
, где  – среднегодовой расход в м3/с, F – площадь водосбора в км2,
– среднегодовой расход в м3/с, F – площадь водосбора в км2, 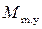 – среднегодовой модуль стока в л/с/км2.
– среднегодовой модуль стока в л/с/км2.
Среднегодовой модуль стока, л/с/км2
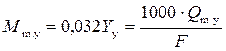 , где
, где  мм,
мм, 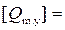 м3/с,
м3/с, 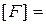 км2.
км2.
Годовой сток в м3
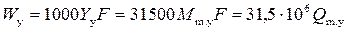 , где
, где  мм,
мм, 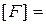 км2,
км2, 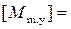 л/с/км2,
л/с/км2, 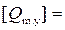 м3/с.
м3/с.
Среднегодовой расход воды в м3/с
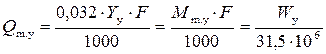 .
.
Основными факторами стока являются климатические. Однако помимо климата на речной сток влияют также геология бассейна реки, его рельеф, почвы, озёра, болота, ледники, вечная мерзлота, величина и форма бассейна, направление течения реки, растительность и т. д. Кроме того, на речной сток оказывает влияние деятельность человека.
К числу климатических элементов относятся осадки, испарение, влажность и температура воздуха. Наблюдения над всеми климатическими элементами производятся на метеостанциях (рис. 5.4.1).

Рис. 5.4.1. Метеостанция.
Основной прибор для измерения осадков – осадкомер Третьякова. Осадкомер представляет собой ведро с площадью приёмной поверхности 200 см², защищенное от выдувания осадков изогнутыми металлическими планками (рис. 5.4.2).

Рис. 5.4.2. Осадкомер.
Для автоматической регистрации выпавших осадков применяется самопишущий прибор плювиограф (рис. 5.4.3). Осадки улавливаются дождемерным ведром 1 площадью 500 см². Из него вода стекает по трубке в специальный сосуд 7 с поплавком 4. Когда уровень воды поднимается, поплавок всплывает вверх. На стержне 2, прикреплённом к поплавку, привинчено перо 3 самописца. Бумажная лента надета на барабан, вращаемый часовым механизмом. После наполнения сосуда вода через сифон 5 выливается в контрольный сосуд 6. По записи на ленте определяют начало и конец дождя, количество выпавшей воды, а следовательно, и интенсивность осадков.
Распределение годового количества осадков по территории Украины показано на рис. 5.4.4.
Рис. 5.4.4. Распределение годового количества осадков по территории Украины.
Контроль за температурой воздуха необходим для расчёта испарения с поверхности воды и суши. Температура воздуха имеет суточные, годовые и многолетние колебания. Суточные изменения температуры характеризуются наличием максимума 13-14 часов, минимума – около рассвета.
Температура почвы следуют за температурой воздуха с некоторым запозданием. Это запоздание увеличивается с глубиной, составляя 2,5…3,5 часа на каждые 10 см. На глубине 1 м суточные температуры остаются постоянными.
Изменение температуры воды, так же как и температуры воздуха, имеют несколько циклов – суточный, годовой и многолетний. Амплитуда изменения температуры воды меньше, чем воздуха.
На рис. 5.4.5 показаны суточные (а) и годовые (б) колебания температуры воздуха в областях с континентальным (I) и приморским (II) климатом.
Распределение средних месячных температур по территории Украины для июля показано на рис. 5.4.6, для января – на рис. 5.4.7.
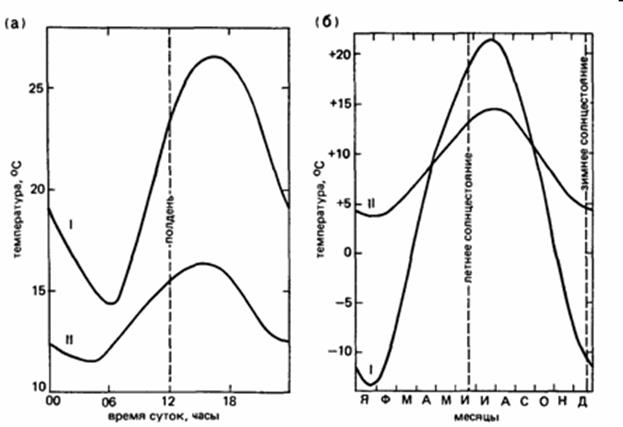
Рис. 5.4.5. Суточные (а) и годовые (б) колебания температуры воздуха в областях с континентальным (I) и приморским (II) климатом.
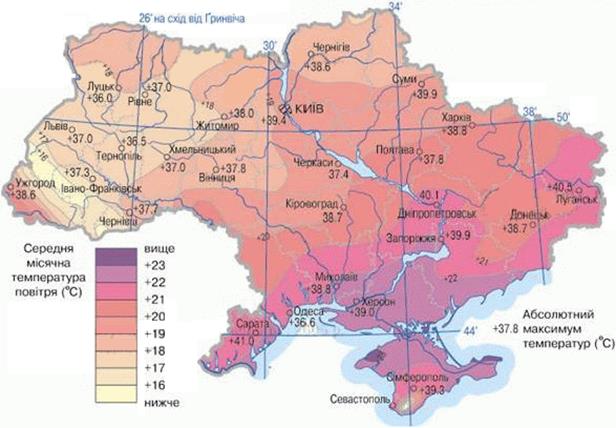
Рис. 5.4.6. Распределение средних месячных температур по территории Украины для июля.
Рис. 5.4.7. Распределение средних месячных температур по территории Украины для января.
Изучение скоростей и направлений ветра представляет интерес для правильного учета величины испарения, определения высоты волн и т.д. Измерения производятся с помощью флюгеров (рис. 5.4.8а), анемометров флюгерных (рис. 5.4.8б) и чашечных (рис. 5.4.8в). Измерение направления фиксируется по 8 румбам (рис 5.4.9).


а б в
Рис. 5.4.8. Измерители скоростей и направлений ветра: а – флюгер, б – флюгерный анемометр, в – чашечный анемометр.
Рис. 5.4.9. Румбы флюгера.
На рис. 5.4.10 показана климатическая карта Украины. На карте показаны изотермы июля и сентября, абсолютные максимумы и минимумы температур в областных центрах. Среднегодовое количество осадков показано цветом. Для ряда городов указаны характеристики ветра. Цифры возле стрелок означают повторяемость ветра определенного направления в процентах от общего числа наблюдений без штилей. Цифрой в центре обозначено среднее количество штилей за период наблюдений. По карте можно определить, что среднегодовое количество осадков в Донецке составляет 550 мм, средняя температура июля 21 °C, декабря –6 °C, абсолютный максимум температуры 39 °C, минимум –34 °C. Характеристики ветра указаны для Луганска: среднее число безветренных дней в году 23, восточный ветер дует в 24% ветреных дней, западный в 18%, северо-восточный в 12% и т. д.
Рис. 5.4.10. Климатическая карта Украины.
Влажность воздуха зависит от количества паров воды, находящихся в нём. Абсолютной влажностьe показывает, какое количество влаги содержится в единице объёма воздуха. Абсолютная влажность может быть выражена в г/м3. Поскольку плотность паров пропорциональна парциальному давлению, то абсолютная влажность может характеризоваться упругостью водяных паров – парциальным давлением 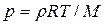 , измеряемым в гектопаскалях. В литературе встречаются также изъятые из употребления единицы давления миллибар и мм ртутного столба (1 мб = 1 гПа; 1 мм рт. ст = 1,333 гПа).
, измеряемым в гектопаскалях. В литературе встречаются также изъятые из употребления единицы давления миллибар и мм ртутного столба (1 мб = 1 гПа; 1 мм рт. ст = 1,333 гПа).
Отношение упругости находящихся в воздухе паров воды e к упругости E паров, насыщающих воздух при данной температуре, называется относительной влажностью: 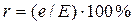 . Значения E берутся из табл. 5.4.1. Так при температуре 20°С E = 23,3 гПа.
. Значения E берутся из табл. 5.4.1. Так при температуре 20°С E = 23,3 гПа.
Таблица 5.4.1. Упругость паров, насыщающих воздух.
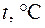 | –5 | |||||||
| E, гПа | 4,0 | 6,1 | 8,8 | 12,3 | 17,1 | 23,3 | 31,7 | 42,7 |
Точка росы – это температура, при которой содержащийся в воздухе пар становится насыщенным. Конденсационный гигрометр (рис. 5.4.11) – прибор для измерения точки росы. Температура полированной поверхности 1 опускается испарением эфира в сосуде до выпадения на этой поверхности росы. Для сравнения поверхность 1 окружена неохлаждаемым кольцом 2.

Рис. 5.4.11. Конденсационный гигрометр.
Из табл. 5.4.1 находят упругость насыщенных паров e в точке росы и E при температуре воздуха. Например, в точке росы 10 °C e = 12,3 гПа, при температуре окружающего воздуха 20 °C E = 23,3 гПа. Относительная влажность: 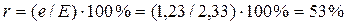 .
.
Разность между упругостью E паров, насыщающих воздух при данной температуре, и упругостью e паров, находящихся в воздухе, называется дефицитом или недостатком влажности: 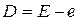 .
.
Для измерения относительной влажности используются также волосяные гигрометры (рис. 5.4.12) и психрометры (рис. 5.4.13).
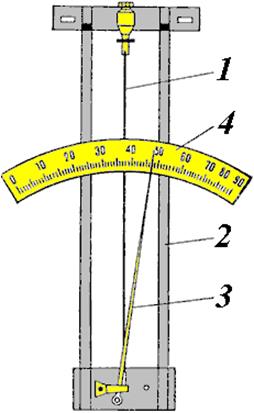
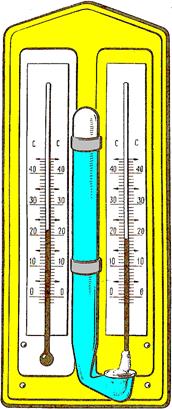
Рис. 5.4.12. Волосяной гигрометр. Рис. 5.4.13. Психрометр.
При использовании психрометра относительная влажность определяется из психрометрической таблицы табл. 5.4.2 по показаниям сухого td и влажного tm термометров. Если, например, td = 20°C, а tm = 16°C, то φ = 66%.
Таблица 5.4.2. Психрометрическая таблица.
Чем выше температура воды, тем больше испарение (рис. 5.4.14). Существуют и перемещения воздушных масс в горизонтальном направлении. На смену влажному воздуху приходит сухой, способный поглотить большее количество влаги, что увеличивает величину испарения. Испарение изучается на специальных бассейнах.
Для малых водоёмов ( 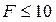 га) испарения с водной поверхности в мм/сут:
га) испарения с водной поверхности в мм/сут:
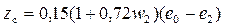 ,
,
где 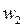 – скорость ветра в м/с на высоте 2 м над поверхностью воды,
– скорость ветра в м/с на высоте 2 м над поверхностью воды, 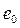 – упругость насыщенного водяного пара при температуре воды на её поверхности в гПа;
– упругость насыщенного водяного пара при температуре воды на её поверхности в гПа; 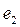 – упругость водяного пара на высоте 2 м над поверхностью воды в гПа.
– упругость водяного пара на высоте 2 м над поверхностью воды в гПа.

Рис. 5.4.14. Испарение с поверхности воды.
Пример 5.4.1. Найти испарение с поверхности водоёма при температуре воды t = 10°C. Скорость ветра над поверхностью воды на высоте 2 м  5 м/с, точка росы на этой высоте tр = 5°C.
5 м/с, точка росы на этой высоте tр = 5°C.
Решение. Согласно табл. 5.4.1 упругость насыщенного водяного пара при температуре воды t = 10°C на её поверхности  12,3 гПа. Согласно табл. 5.4.1 точке росы tр = 5°C соответствует упругость водяного пара
12,3 гПа. Согласно табл. 5.4.1 точке росы tр = 5°C соответствует упругость водяного пара 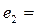 8,8 гПа. Испарения с водной поверхности
8,8 гПа. Испарения с водной поверхности
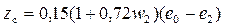 = 0,15(1 0,72·5)·(12,3 – 8,8) = 2,42 мм/сут.
= 0,15(1 0,72·5)·(12,3 – 8,8) = 2,42 мм/сут.
В зимнее время испарение невелико и составляет 6–8% от годовой суммы и им часто пренебрегают.
Тяжелые почвы (глинистые и тяжелосуглинистые) лучше увлажняются капиллярными токами и интенсивнее испаряют влагу, чем лёгкие (супесчаные и песчаные).
Поверхность земли, затенённая растениями, меньше нагревается, а скорость ветра в приземном слое незначительна. Поэтому здесь испаряется влаги меньше, чем с открытой поверхности. Чем гуще растительный покров, тем меньше испарение с поверхности почвы. На рис. 5.4.15 показан выращенный в Волновахском районе в голой степи Великоанадольский лес.

Рис. 5.4.15. Великоанадольский лес сохраняет почвенную влагу.
Процесс испарения воды растениями называется транспирацией. Сумма же испарения с поверхности почвы и транспирации называется суммарным водопотреблением, или суммарным испарением. Эта величина выражается в м3/га или в мм слоя воды, испаряющейся за определённый промежуток времени: за сутки, месяц и год.
На рис. 5.4.16 показано распределение среднего годового слоя испарения в миллиметрах по территории Украины.
Дополнительные факторы стока:
1. Площадь водосбора. Чем больше площадь, тем больше сток.
2. Рельеф водосбора. Круче рельеф – больше скорость стекания осадков.
3. Густота речной сети. С увеличением густоты речной сети модуль стока возрастает.
4. Почвенно-геологические условия – инфильтрация.
5. Растительный покров. Равномерный сток, больше осадков, меньше испарение.
6. Озера способствуют уменьшению максимальных расходов воды, являются регуляторами стока.
7. Ледники при сезонном таянии формируют реки.
8. В районах вечной мерзлоты сток неравномерен. Грунтовое питание мало, реки промерзают.
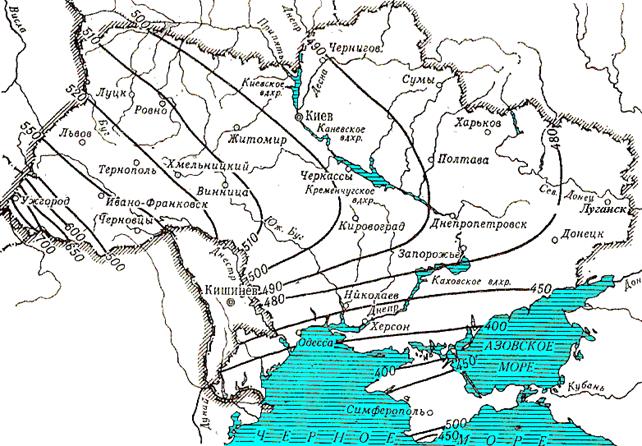
Рис. 5.4.16. распределение среднего годового слоя испарения в миллиметрах по территории Украины.
Уровень воды – положение свободной водной поверхности над условной горизонтальной плоскостью сравнения (неизменной по высоте).
По условиям питания все реки делятся на следующие типы:
1. Реки снегового питания – подавляющее большинство рек, весной 50–100% годового стока.
2. Реки дождевого питания – Крым, Карпаты.
3. Реки ледникового питания – Средняя Азия, Камчатка, Кавказ.
4. Реки смешанного питания.
Любая река, независимо от типа питания несет в разное время разное количество воды.
Амплитуда колебания различна. Волга – до зарегулирования у Твери 12 м, у Самары – 15 м, у Астрахани – 4 м. В низовьях колебания уровня меньше, так как больше глубина и шире устье.
График колебания расхода называется гидрографом реки. Положение уровней фиксируется на водомерных постах. Гидрограф реки Днестр на водомерном посту № 1 (в верховьях) показан на рис. 5.4.17.
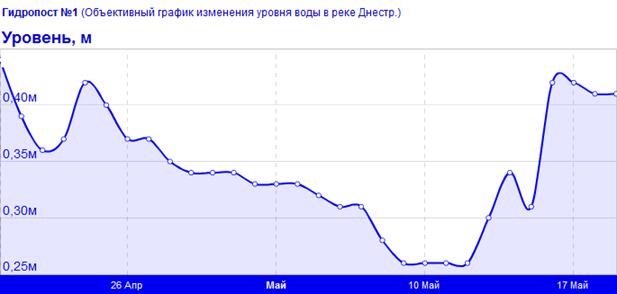
Рис. 5.4.17. Гидрограф Днестра на водомерном посту № 1.
Половодье – ежегодно повторяющееся в одно и то же время высокое стояние уровней, вызванное таянием снега, дождями, ледниками. Продолжительность половодья – у малых рек – 5…20 дней, у больших – 1,5…7 месяцев.
Паводок (рис. 5.4.18) – быстрое и кратковременное поднятие уровня из-за неожиданного сильного дождя или снеготаяния. Продолжительность паводка – от нескольких часов до нескольких месяцев.


Рис. 5.4.18. Паводок.
ТЕМА 5.5. Речные наносы
Вода, стекая с поверхности бассейна, захватывает при своём движении частицы почвы или грунта. Явление смыва почвенных частиц стекающими талыми или ливневыми водами называется водной эрозией почв (рис. 5.5.1). Водная эрозия зависит от характера почвенного покрова, состояния поверхности почвы, рельефа, величины стока и т. д. Смыв ослабляется, если почва защищена густым травянистым покровом и лесом, но возрастает с увеличением уклонов.

Рис. 5.5.1. Водная эрозия почвы.
Продукты поверхностного смыва, попадая в реку, смешиваются с продуктами размыва дна и берегов русла, образуя наносы реки. Вода перемещает наносы во взвешенном состоянии или влечёт их по дну. Влекомые наносы называются также донными.
Количество взвешенных наносов, приходящихся на единицу объёма воды, называется мутностью: ρ = m/V, где ρ – мутность в г/л (кг/м³), m – масса наносов в пробе воды в граммах, V – объём пробы речной воды в литрах. На рис. 5.5.2 показаны результаты измерения на протяжении года мутности воды на входе и на выходе водоочистных сооружений. Мутность на входе минимальна в зимние месяцы и достигает максимума в период весеннего половодья. Флокулянты – вещества, добавляемые в очищаемую воду. Они способствуют объединению коллоидных частиц в рыхлые хлопьевидные агрегаты – флоккулы, задерживаемые затем фильтрами.
Расход наносов – количество твёрдого вещества, переносимого водой через живое сечение реки в единицу времени: r = m/t = ρQ; [r] = кг/с.
Расход наносов неравномерен на протяжении года. Он максимален весной (в половодье) и возрастает в период дождей.
Наивысшие показатели твердого стока и мутности воды имеют горные реки Украинских Карпат и Крыма, а также реки, пересекающие возвышенности лесостепи и степи. Наименьший твердый сток у рек лесной зоны. Карта мутности рек Украины приведена на рис. 5.5.3. Твердый сток постепенно откладывается в виде наносов ниже течению и выносится главными реками в моря или озёра. Там он накапливается на дне или откладывается в устьях рек в виде островов, образующих дельту.
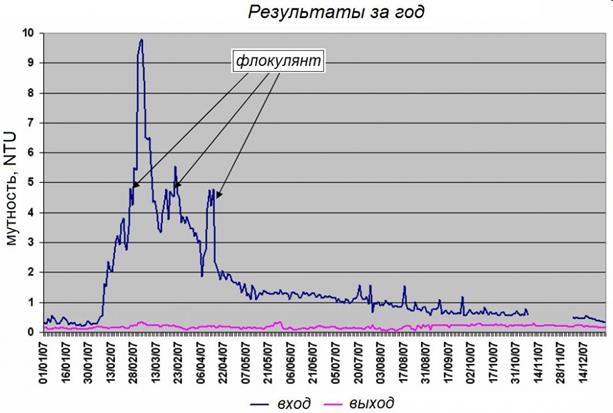
Рис. 5.5.2. Мутность воды на входе и на выходе водоочистных сооружений.
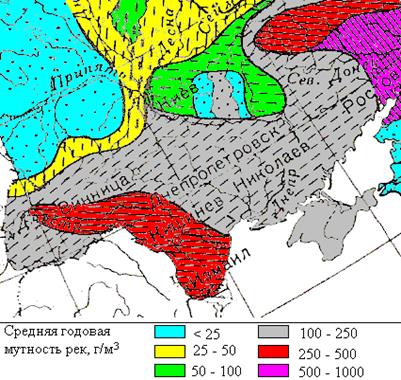
Рис. 5.5.3. Карта мутности рек Украины.
Наносы вызывают затруднения в эксплуатации гидротехнических сооружений и в судоходстве.
При выпадении сильных ливней на горных склонах реки превращаются в грязекаменные потоки, называемые селями, или селевыми потоками. На рис. 5.5.4 показан сель в Карпатах.

Рис. 5.5.4. Сель в Карпатах.
Наносные образования в русле (рис. 5.5.5) наблюдаются, главным образом, у равнинных рек. Наиболее характерный вид отложения наносов – коса (1), которая образуется у выпуклого берега в виде клина, идущего под углом вниз по течению. Коса постепенно уходит под воду, далеко вдаваясь в русло реки. Заструги (2) – это подводные песчаные наносы в виде зубьев у нижней оконечности косы, которые иногда тянутся до противоположного берега. Небольшой залив между косой и берегом, обычно у верхнего плеча яра, называют затониной (3). На рисунке видны также песчаный островок в русле – осередок (4) и песчаная мель – высыпка (5).
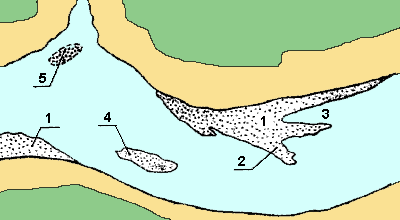
Рис. 5.5.5. Наносные образования: 1 – коса, 2 – заструги, 3 – затонина, 4 – осередок, 5 – высыпка.
Дельта (рис. 5.5.6) – сложенная речными наносами низменность в низовьях реки, прорезанная разветвлённой сетью рукавов и протоков.
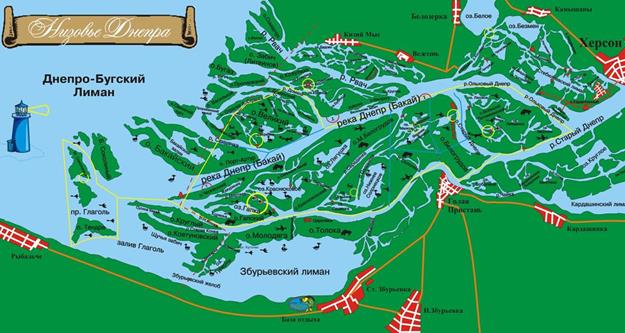
Рис. 5.5.6. Дельта Днепра.
Болота образуются при зарастании водохранилищ: озёр, речных стариц, заводей. Вследствие отложения ила на дне озера, так называемого сапропеля, и выноса в озеро минеральных и органических веществ, смытых с площади водосбора, происходит постепенное обмеление озера. Оно начинает от берегов зарастать водной растительностью, которая отмирает со временем и падает на дно. Это оказывает содействие дальнейшему обмелению озера. Со временем водная растительность покрывает все озеро и образуется болото с характерной водолюбивой растительностью. Насыщенная водой отмирающая растительность вследствие недостатка в воде кислорода полностью не разлагается и превращается в торф.
Болото (рис. 5.5.7) имеет ряд гидрологических особенностей по сравнении с озером, рекой и сушей. В торфяных болотах вмещается от 89 до 94% воды и лишь 11-6% сухого вещества, которое и удерживает в болоте такое огромное количество воды. Связанность воды в болоте сухим веществом торфа исключает возможность ее использования для дополнительного питания рек.
§
ТЕМА 6.1. Гидрометрические работы
Гидромéтрия (др.-греч. ϋδωρ — вода и μετρέω — измеряю) — раздел гидрологии суши, занимающийся измерением элементов гидрологического режима, способами и приборами этих измерений, а также методами обработки полученных результатов, их сбора, хранения и публикации.
Гидрометрией также называется совокупность методов определения величин, характеризующих движение и состояние жидкости и режим водных объектов.
К задачам гидрометрии относятся измерения: уровней, глубин, рельефа дна и свободной поверхности потока; напоров и давлений; скоростей и направлений течения жидкости; пульсаций скоростей и давлений; элементов волн; гидравлических уклонов; мутности потока (концентрации наносов); расходов воды, наносов и гидросмеси; элементов, характеризующих термический и ледовый режим потоков и др.
Для наблюдения за уровнями воды в реках, водохранилищах устраивают водомерные посты. Их назначение – определение и фиксация колебаний уровня. Кроме того фиксируются температура воды, воздуха, ледовые явления, растительность и т. п.
В зависимости от наблюдаемого объекта и установленного объёма наблюдений, гидрологические посты имеют определённый тип и разряд:
гидрологические посты на реках и каналах — ГП. Делятся на ГП: 1-го (ведущие полный объем наблюдений) и 2,3-го разряда (уровенные посты и работающие по сокращенной программе)
озерные гидрологические посты на озерах и водохранилищах — ОГП
морские гидрологические посты на морях — МГП.
На гидрологическом посту проводятся следующие виды наблюдений:
уровень воды на водном объекте (все типы)
уклон водной поверхности (ГП-1)
расход воды в реке или канале (ГП-1)
температура воды (все типы)
мутность воды (ГП, ОГП)
расход взвешенных и донных наносов (ГП-1)
волнение (МГП, ОГП)
рейдовые наблюдения на акваториях (ОГП, МГП)
соленость воды (МГП)
мониторинг загрязнения вод (все типы)
Кроме того, часть постов осуществляет так же и метеонаблюдения: температура воздуха, осадки, снегосъемка и пр.
Размещение водомерных постов вдоль Прута и Днестра показано на рис. 6.1.1. Гидрологические показатели Днестра, фиксируемые на этих постах, показаны рис. 5.3.11
Рис. 6.1.1. Размещение водомерных постов вдоль Прута и Днестра.
Посты могут быть постоянными (действующими не менее года) и временными.
Типы постов по устройству:
• реечные;
• свайные;
• смешанные;
• автоматические.
На каждом посту устанавливается постоянный репер, «привязанный» к ближайшему реперу государственной сети. Репер (от фр. repere – знак, исходная точка) – знак, закрепляющий точку земной поверхности, высота которой относительно исходной уровенной поверхности определена путем нивелирования. Репер показан на рис. 6.1.2, а триангуляционный пункт, на котором он установлен – на рис. 6.1.3.

Рис. 6.1.2. Репер государственной сети.

Рис. 6.1.3. Триангуляционный пункт.
Высоты реперов вычисляются относительно нуля Кронштадтского футштока (рис. 6.1.4). Нуль Кронштадтского футштока представляет собой многолетний средний уровень Балтийского моря. Реперы государственной нивелирной сети служат исходными (опорными) пунктами для определения высот промежуточных точек земной поверхности при топографических съемках и разного рода изыскательских работах, а также используются в научных целях при изучении разности уровней морей.

Рис. 6.1.4. Кронштадтский футшток.
Реечный водомерный пост (рис. 6.1.5) состоит из одной или нескольких надёжно закреплённых реек. Обычно рейки крепят к забитым в грунт сваям, к стенкам набережных, устоям и быкам мостов в защищенном от ледохода и судов месте. На рис. 6.1.5 1 – укреплённая на свае рейка; 2 – ледорез для защиты рейки от плавающих предметов.
Для получения точного отсчёта уровня, например во время волнения, рейку устанавливают в ковше берега, соединённом с руслом канавкой (рис. 6.1.6).
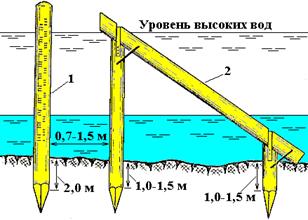
Рис. 6.1.5. Реечный водомерный пост.
Рис. 6.1.6. Рейка в ковше берега.
Часто пользуются наклонными рейками (рис. 6.1.7), у которых деревянный брус укреплён на сваях по откосу берега. Здесь 1 – наклонная рейка, 2 – щебёнчатая подготовка, 3 – сваи.
Каждое деление наклонной рейки 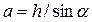 , где h = 1 см. Эти рейки лучше вертикальных защищены от ледохода; они не создают подпора; отсчёт по ним более точен.
, где h = 1 см. Эти рейки лучше вертикальных защищены от ледохода; они не создают подпора; отсчёт по ним более точен.
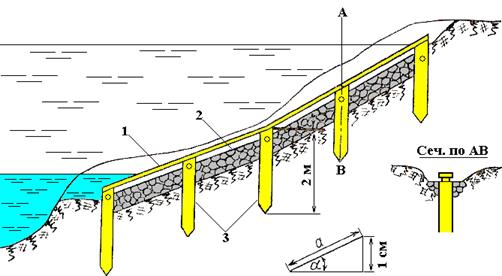
Рис. 6.1.7. Водомерный пост с наклонными рейками.
Свайные водомерные посты (рис. 6.1.8) состоят из ряда свай, забитых в дно и берег перпендикулярно к среднему направлению течения воды. Сваи нумеруют в направлении от репера водомерного поста, устанавливаемого в незатопляемой зоне берега. Головки свай спиливают горизонтально. В центре головки сваи забивают корабельный гвоздь.
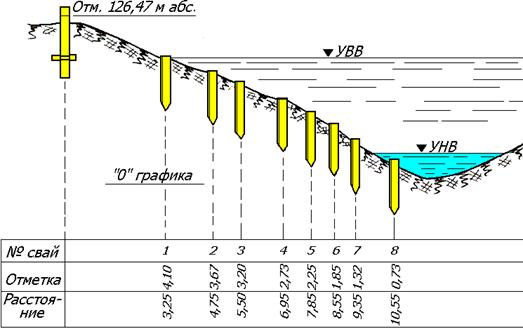
Рис. 6.1.8. Свайный водомерный пост.
После установки свай измеряют расстояние между ними; сваи нивелируют и «привязывают» к отметке репера водомерного поста.
Смешанные водомерные посты (реечно-свайные) (рис. 6.1.9) устанавливают на реках с широкой затопляемой поймой. Здесь1 – линия промерзания грунта, 2 – наинизший уровень воды, 3 – сваи, 4 – водомерные рейки.
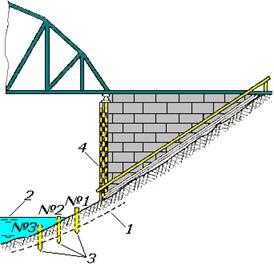
Рис. 6.1.9. Реечно-свайный водомерный пост.
На рис. 6.1.10 показана кинематическая схема самописца уровня «Валдай». Здесь 1 – груз, 2 – поплавок, 3 – противовес, 4 и 5 – поплавковое колесо, 6 – шестерня, 7 – часовой механизм, 8 – барабан, 9 – ролик, 10 – каретка, 11 – струна, 12 – направляющие стержни, 13 – ролик, 14 – груз, 15 – перо, 16 – барабан, 17 – шестерня.
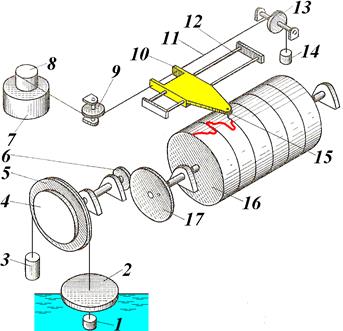
Рис. 6.1.10. Кинематическая схема самописца уровня «Валдай».
На рис. 6.1.11 показан береговой самописец уровня воды. Здесь 1 – будка, 2 – труба, 3 – колодец, 4 – рейка, 5 – столик, 6 – самописец уровня, 7 – барабан.
Рис. 6.1.11. Береговой самописец уровня воды.
Дистанционный гамма-уравнемер (рис. 6.1.12) состоит из источника излучения (датчик уровня) 1, укреплённого на поплавке 4, приёмника (детектор) 3 и счётного механизма 2. Источником является радиоактивный изотоп, помещённый на поплавке. Интенсивность излучения обратно пропорциональна квадрату расстояния между источником и приёмником. При опускании уровня расстояние увеличивается, воздействие гамма-лучей на детектор ослабляется. Такие уравнемеры устанавливаются в малонаселённых местах. Данные передаются на гидрологические станции автоматически по радио.
Рис. 6.1.12. Дистанционный гамма-уравнемер.
График колебаний уровня воды и условные обозначения ледовой обстановки показаны на рис. 6.1.13. Здесь 1 – «сало», 2 – забереги, 3 – сало при заберегах, 4 – редкий шугоход, 5 – шугоход, 6 – редкий ледоход, 7 – ледоход, 8 – неподвижный ледяной покров, 9 – вода течёт поверх льда, 10 – закраины, лёд поднят, 11 – дата зажора или затора, 12 – дата подвижки льда.
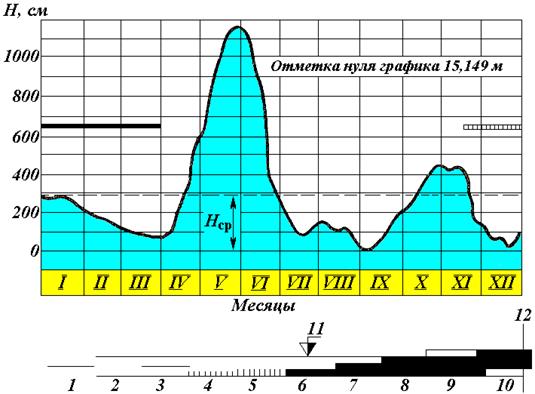
Рис. 6.1.13. График колебаний уровня воды на водомерном посту.
«Сало» (рис. 6.1.14) – это поверхностные первичные ледяные образования в виде серых масляных пятен или тонкого сплошного слоя, состоящие из иглообразных или пластинчатых кристаллов.
Забереги (рис. 6.1.15) – это полосы льда, смёрзшиеся с берегами водных объектов при незамёрзшей основной части водного пространства.


Рис. 6.1.14. Сало. Рис. 6.1.15. Забереги.
Шугá – всплывший на поверхность или занесённый вглубь потока внутриводный лёд в виде комьев, ковров, венков и подлёдных скоплений. Движение шуги по поверхности и внутри водного потока именуется шугоходом (рис. 6.1.16).
Ледоход (рис. 6.1.17) – движение льдин и ледяных полей (льдин размером более 100 м по наибольшему измерению) на реках и водохранилищах под влиянием течений.


Рис. 6.1.16. Шугоход. Рис. 6.1.17. Ледоход.
Закраины (рис. 6.1.18) – полосы открытой воды у берегов, образующиеся перед вскрытием реки.
Зажор (рис. 6.1.19) – возникающее во время осеннего ледохода скопление шуги с мелкобитым льдом в русле реки, вызывающее стеснение водного сечения и связанный с этим подъём уровня воды. Формирование зажоров иногда происходит в течение нескольких суток и сопровождается подвижками льда (перемещением ледяного покрова на отдельных участках реки) в течение часа и больше. В результате возникает нагромождение льда на берегах и на поверхности ледяного покрова (торосы).


Рис. 6.1.18. Закраины. Рис. 6.1.19. Зажор.
Затор (рис. 6.1.20) – возникающее во время весеннего ледохода скопление льдин в русле реки, вызывающее стеснение водного сечения и связанный с этим подъём уровня воды.

Рис. 6.1.20. Затор.
Створ через водоток в месте водомерного поста, перпендикулярный среднему направлению течения воды, называется гидрометрическим створом (рис. 6.1.21). На гидрометрических створах измеряют расходы воды и наносов. Поэтому здесь должна быть высокая точность измерения площадей живых сечений и т. д.
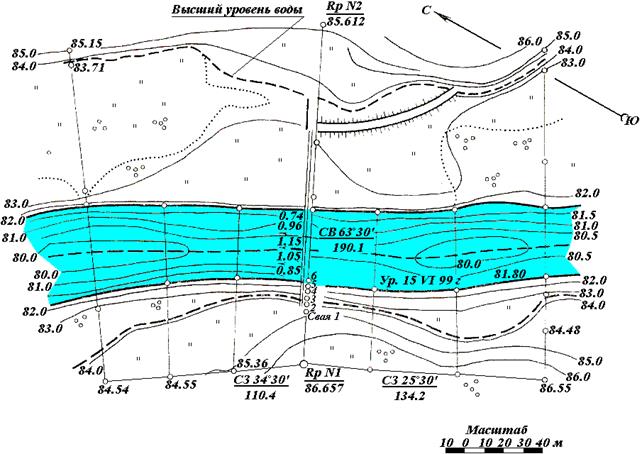
Рис. 6.1.21. Гидрометрический створ.
Направление створа должно быть перпендикулярным к направлению течения воды в русле. С этой целью на берегу реки разбивают базис ABD параллельно берегу (рис. 6.1.22). Из точек А и В восстанавливают перпендикуляры АМ1 и BN1. Линии АМ1 и BN1 закрепляют тремя вехами каждую. На базисе в точке D устанавливают угломерный инструмент (теодолит или мензулу). Ноль лимба совмещают с направлением базиса. Из лодки пускают последовательно ряд поплавков, которые проходят через створы АМ1 и BN1 в разных точках. Поплавки в этих точках засекают инструментом. О моменте прохождения поплавков через створы сигнализируют наблюдатели, находящиеся в точках А и В. Направления хода поплавков переносят на план, после чего уточняют направление базиса АСЕ, параллельное среднему направлению хода поплавков. Створ BN разбивают перпендикулярно базису АЕ. Створ закрепляют двумя реперами на правом и левом берегах.
Для производства гидрометрических работ в створе устанавливают перекидные или подвесные мостики, используют лодки, паромы и подвесные люльки.
На узких реках и каналах шириной до 15 м устраивают перекидные мостики (рис. 6.1.23). Здесь а – план, б – фасад, в – поперечный разрез.
Рис. 6.1.22. Определение направления створа.
При ширине русла, превышающей 15 м, используют подвесные мостики (рис. 6.1.24). Здесь 1 – мёртвый якорь, 2 – тросы, 3 – подпорная рама, 4 – бруски, 5 – настил.
Рис. 6.1.23. Перекидной мостик.
Рис. 6.1.24. Подвесной мостик.
На реках с быстрым течением, резкими колебаниями уровней и высокими берегами применяют подвесные люльки (рис. 6.1.25). В люльке обычно помещаются один-два человека с необходимыми гидрометрическими приборами. Здесь 1 – стойка, 2 – перекидной трос, 3 – люлька, 4 – вертушка.
Рис. 6.1.25. Подвесная люлька.
Дистанционные измерения на створах (глубин, скоростей течения и взятие проб воды) производится с помощью гидрометрической установки ГР-64 (рис. 6.1.26). Здесь 1 и 4 – стойки, 2 – трос, 3 – каретка, 5 – вертушка, 6 – лебёдка, 7 – электродвигатель.
Рис. 6.1.26. Гидрометрическая установка ГР-64.
На реках шириной более 150-200 м паромы закрепляют якорями (рис. 6.1.27). Для перемещения паромов используют моторные суда. Здесь 1 – ездовой трос, 2 – блок с петлёй, 3 – лодка, 4 – помост.
При производстве промеров в зависимости от глубин и скоростей течения воды применяются различные приборы. Небольшие глубины замеряют водомерной рейкой (рис. 6.1.28). Для измерения глубин до 7-8 м при относительно небольших скоростях служит намётка – окованный снизу башмаком шест длиной до 10 м и диаметром 4-6 см. Если дно илистое, намётку снабжают диском диаметром 20-25 см, который предупреждает погружение намётки в илистое дно. Лот (рис. 6.1.29) представляет собой чугунный или свинцовый груз, подвешенный к размеченному шнуру или лотлиню. Момент соприкосновения лота со дном устанавливают по уменьшению натяжения лотлиня или по сигналу от электрического поддона, расположенного под грузом.
Рис. 6.1.27. Паром.


Рис. 6.1.28. Водомерная рейка. Рис. 6.1.29. Лот.
Вследствие относа лотлиня при больших скоростях течения (рис. 6.1.30) истинная глубина h меньше измеренной (длины лотлиня ACB) h = ACB – z – ΔH1– ΔH2, где z – высота подвеса троса над водой, ΔH1= z(1/cosβ – 1), ΔH2 – поправка, найденная из табл. 6.1.1.
Рис. 6.1.30. Относ лотлиня течением.
Таблица 6.1.1. Определение глубины по показания лотлиня.
| ACB, м | Угол отклонения троса β, градус | ||||
| 0,01 | 0,02 | 0,04 | 0,06 | 0,09 | |
| 0,04 | 0,08 | 0,14 | 0,22 | 0,31 | |
| 0,05 | 0,15 | 0,25 | 0,40 | 0,60 | |
| 0,10 | 0,20 | 0,40 | 0,55 | 0,80 |
По отметкам дна и расстояния между промерными вертикалями строят поперечный профиль русла (рис. 6.1.31). Поперечный профиль вычерчивают в искажённом масштабе: вертикальный масштаб принимают в 10 или 100 раз больше горизонтального. Наносят отметки дна или откладывают глубину вниз от рабочего уровня. На профиле показывают рабочий, наивысший и наинизший уровни, репера и их отметки. Отметки берега, не покрытого водой, наносят на профиль по материалам нивелировки.
В поперечном сечении реки возможны небольшие участки мёртвого пространства, в котором отсутствует течение. Вся остальная площадь поперечного сечения между дном и поверхностью воды, в которой скорости наблюдаются во всех точках, называется живым сечением, в отличие от водного сечения, занимаемого водой. Площадь водного сечения реки можно определить планимéтром или аналитически – суммированием площадей фигур, ограниченных промерными вертикалями.
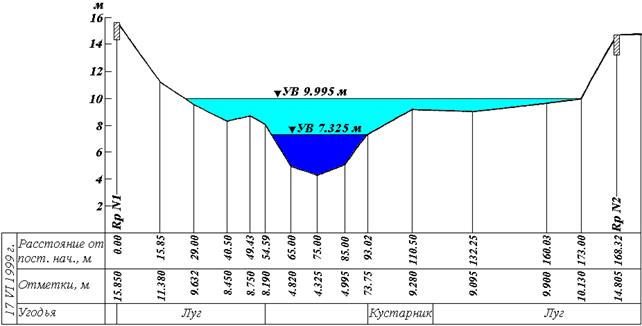
Рис. 6.1.31. Поперечный профиль русла.
С изменением уровня воды изменяется и площадь водного сечения. Зависимость площади ω от высоты H стояния уровня воды выражают графически кривой площадей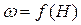 (рис. 6.1.32).
(рис. 6.1.32).
Для измерения скорости течения воды служат поплавки, батометры, вертушки и динамометры.
Поверхностные поплавки (рис. 6.1.33а) – это деревянные кружки с флажком яркого цвета (размеры указаны в сантиметрах). Для поплавков используют и бутылки, погружённые так, что на поверхности находится лишь горлышко с флажком. На широких реках применяют деревянные поплавки с подвешенным грузом.
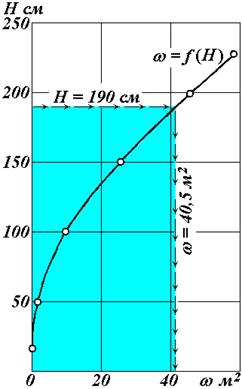
Рис. 6.1.32. Кривая площадей.
Глубинные поплавки (рис. 6.1.33б) состоят из двух: одного крупного, погружённого в воду на определённую глубину, и поверхностного мелкого, перемещающегося со скоростью глубинного и служащего указателем хода. Иногда глубинные поплавки состоят из двух поплавков одинакового размера. В этом случае средняя скорость равна полусумме поверхностной скорости и скорости на глубине: vср = (u0 uгл)/2. Отсюда uгл = 2vср – u0.
Гидрометрические шесты (рис. 6.1.33в) применяют на участках рек с постоянной глубиной. Они служат для определения средней скорости на вертикали. Их свинчивают из металлических полых труб разной длины. Нижнюю часть трубу заполняют дробью для погружения поплавка на 0,95 глубины вертикали.
Поплавок-интегратор более точно (чем шест) измеряет среднюю скорость по вертикали. Поплавок из дерева или другого лёгкого материала отпускается на глубине. Поплавок всплывает через время t на расстоянии L от штанги. Средняя скорость на вертикали vв = L/t.
Гидрометрическая вертушка (рис. 6.1.34) наиболее точный прибор для измерения скоростей в отдельных точках. Основные конструктивные элементы вертушки – чашечный ротор 1 с вертикальной осью вращения, счётно-контрольный механизм, хвостовое оперение 3. Груз обтекаемой формы 2 также снабжён хвостовым оперением. Вертушка крепится на штанге или подвешивается на тросе.
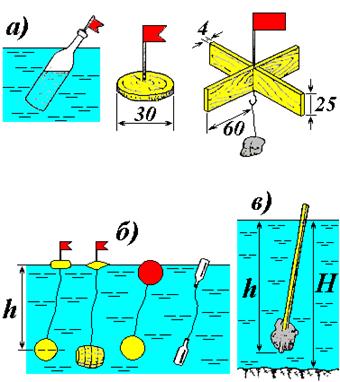
Рис. 6.1.33. Устройства для измерения скорости течения: а – поверхностные поплавки, б – глубинные поплавки, в – гидрометрические шесты.

Рис. 6.1.34. Гидрометрическая вертушка.
Скорости измеряют в разных точках на отдельных скоростных вертикалях. По данным этих измерений вычисляют среднюю скорость на вертикали. Распределение скоростей по вертикали изображают построением эпюры скоростей (рис. 6.1.35). По вертикальной оси отложены глубины в метрах. В местах измерения скоростей по горизонтали отложены измеренные осреднённые скорости в м/с. Концы горизонтальных отрезков соединены плавной кривой.
На нашей эпюре средняя скорость по вертикали vв = Σu/n = 6,53/10 = 0,653 м/с. Она представляет собой частное от деления площади эпюры на глубину. Площадь эпюры можно заменить равновеликой площадью прямоугольника, у которого ширина равна средней скорости vв, а высота – глубине вертикали h.
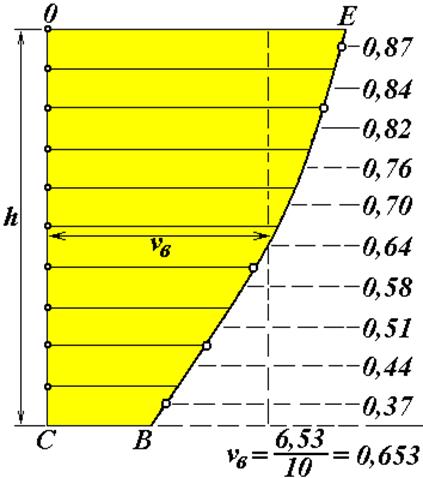
Рис. 6.1.35. Эпюра скоростей.
На поперечном сечении реки изображают изотахи – линии одинаковых скоростей (рис. 6.1.36). В открытом русле (а) наибольшие скорости размещаются на поверхности самой глубокой вертикали. Дополнительная шероховатость, создаваемая ледяным покровом, является причиной перемещения наибольшей скорости вглубь от нижней поверхности льда (б).
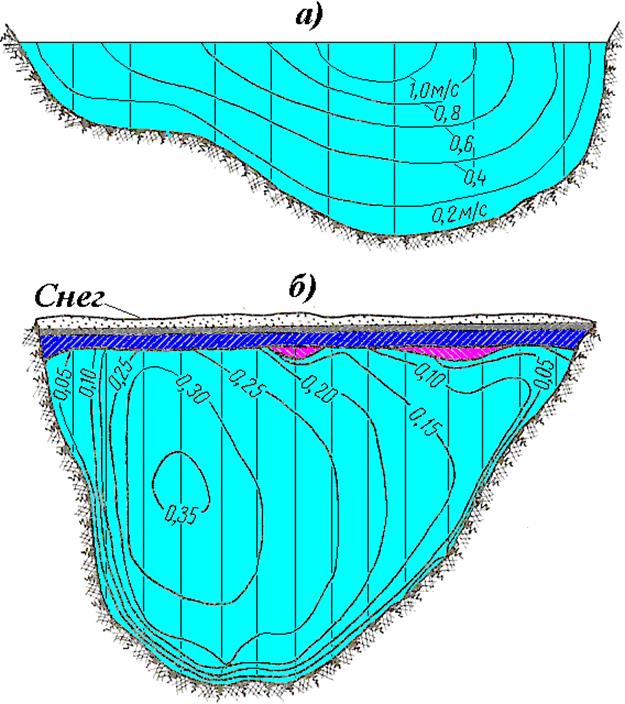
Рис. 6.1.36. Изотахи (линии равных скоростей) в поперечном сечении реки: а – при открытой воде, б – подо льдом.
§
На рис. 6.2.1 изображена модель расхода жидкости: А – объём, равный расходу, Б – тот же объём и расходы воды на вертикалях (заштрихованы). Во всех точках живого сечения восстановлены перпендикуляры длиной u и через концы этих векторов проведена поверхность. Эта поверхность, живое сечение AFEDC, свободная поверхность AMGNC и смоченная поверхность образуют объём, численно равный расходу Q. Такой объём называется моделью расхода потока жидкости.

Рис. 6.2.1. Модель расхода воды.
Пересекая модель расхода вертикальными плоскостями, расположенными по направлению течения, получим профили скоростей u = u(y), например BGKHEB. Если плоскости располагать параллельно живому сечению, получим изотахи, например MLHNN. При пересечении модели расхода плоскостями, параллельными поверхности воды, получим распределение скоростей по ширине потока u = u(b), например FLKDF. При условии y = h имеем эпюру распределения поверхностных скоростей AMGNCBA.
Для расчёта расхода по профилям скоростей строят профиль живого сечения (рис. 6.2.2), на котором обозначают флажками скоростные вертикали. На этом же чертеже строят профили скоростей u = u(y) (для примера показан профиль вертикали 5). Площади профилей скоростей равны удельным (на единицу ширины реки) расходам q на скоростных вертикалях. Средняя скорость на вертикали uв= q/h. Затем строят эпюру uв= uв(b), называемуюэпюрой распределения средних на вертикалях скоростей по ширине потока, откладывая uввверх от линии уровня воды. Откладывая q = uвh вверх от поверхности воды и проводя плавную кривую, строят эпюру распределения расходов на вертикалях по ширине потока q = qв(b). Площадь этой эпюры численно равна расходу Q.
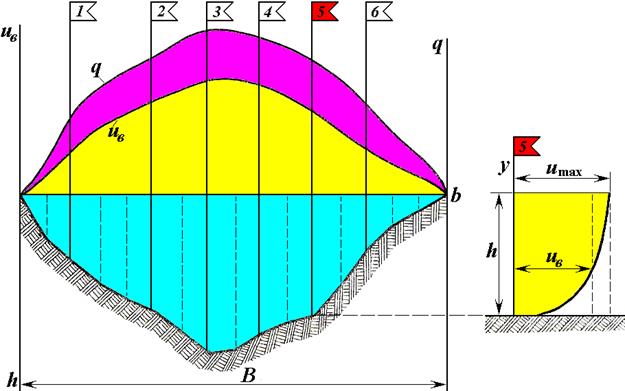
Рис. 6.2.2. Профиль живого сечения.
Пример 6.2.1. Определить расхода воды в русле реки. Результаты измерения глубин h на расстояниях x от постоянного начала на берегу приведены в табл. 6.2.1 (здесь Δx – шаг промеров) и на графике рис. 6.2.3.
Таблица 6.2.1. Глубины h на расстояниях x от постоянного начала.
| x, м | 2,23 | 2,50 | 3,00 | 3,50 | 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 8,89 |
| Δx, м | 0,27 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,39 | |
| h, м | 0,00 | 0,78 | 1,05 | 1,10 | 1,15 | 1,25 | 1,32 | 1,40 | 1,62 | 2,00 | 2,20 | 2,10 | 2,05 | 1,60 | 0,00 |
Решение. Ширина реки 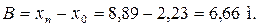
Максимальная глубина 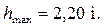
Площадь водного сечения 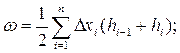
ω = [0,27(0,00 0,78) 0,5(0,78 1,05) … 0,39(1,60 0,00)]/2 = 9,63 м2.
Средняя глубина hср = ω/B = 9,63/6,66 = 1,45 м.
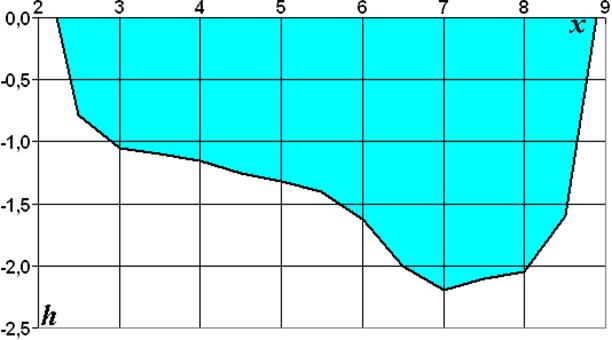
Рис. 6.2.3. Поперечный профиль русла для примера 6.2.1.
Результаты измерения скоростей u в зависимости от глубины h на расстоянии x = 3 м от постоянного начала на берегу и профиль скоростей вертикали, соответствующей x = 3 м, приведены на рис. 6.2.4. Скорости на поверхности при h = 0,00 м и у дна при h = 1,05 м из-за ограничений присущих вертушке находим численной или графической экстраполяцией.
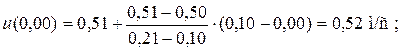
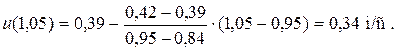
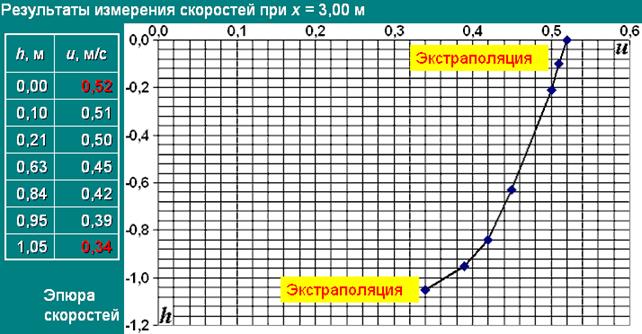
Рис. 6.2.4. Зависимость скорости от глубины для вертикали x = 3 м.
Средняя по вертикали скорость  ;
;
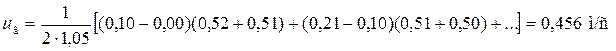 .
.
Удельный (на единицу длины) расход на вертикали находим, перемножая глубину и скорость на вертикали:
q = huvв = 1,05·0,456 = 0,479 м³/с/м.
Точно так же строим эпюры и выполняем расчёты для других вертикалей. Результаты расчётов и графики распределения глубины, скорости и удельного расхода на вертикалях приведены на рис. 6.2.5.
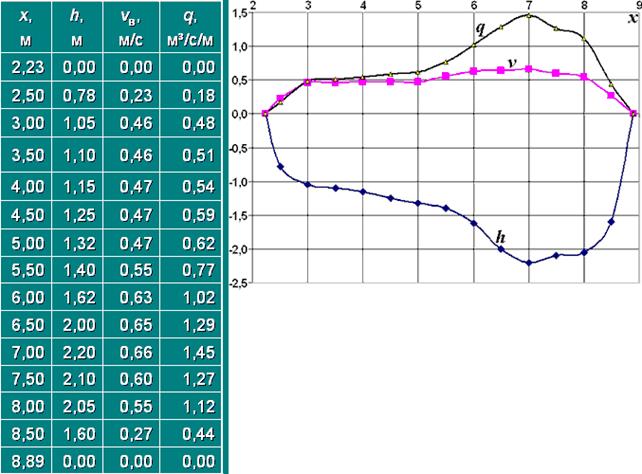
Рис. 6.2.5. Эпюры средней скорости по вертикали и удельного расхода на поперечном профиле русла.
Расход воды в изучаемом сечении  ;
;
Q = 0,5[0,27(0,00 0,18) 0,50(0,18 0,48) … = 5,10 м³/с.
Средняя скорость в сечении V = Q/ω = 5,10/9,63 = 0,53 м/с.
Определение расхода по скоростям поверхностных поплавков.
Строят профиль живого сечения 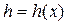 , на котором обозначают флажками места пересечения створа поплавками (рис. 6.2.6). На этом же чертеже строят эпюру поверхностных скоростей поплавков uп= uп(y) в виде плавной кривой. Перемножение ординат двух эпюр – глубин и поверхностных скоростей – на всех промерных вертикалях даёт третью – эпюру фиктивных удельных расходов qф. Фиктивный расход потока Qф равен площади этой эпюры. Действительный расход Q = k1Qф. В рекогносцировочных расчётах коэффициент k1 = 0,85. Более точное значение k1 = С/(С 6), где C – коэффициент Шези:
, на котором обозначают флажками места пересечения створа поплавками (рис. 6.2.6). На этом же чертеже строят эпюру поверхностных скоростей поплавков uп= uп(y) в виде плавной кривой. Перемножение ординат двух эпюр – глубин и поверхностных скоростей – на всех промерных вертикалях даёт третью – эпюру фиктивных удельных расходов qф. Фиктивный расход потока Qф равен площади этой эпюры. Действительный расход Q = k1Qф. В рекогносцировочных расчётах коэффициент k1 = 0,85. Более точное значение k1 = С/(С 6), где C – коэффициент Шези: 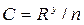 .
.
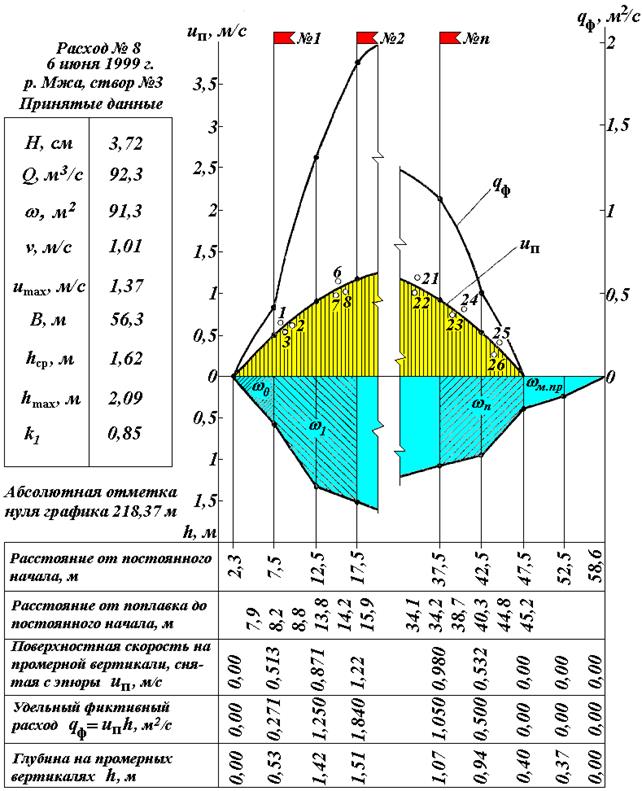
Рис. 6.2.6. Определение расхода по скоростям поверхностных поплавков.
§
Пробы воды отбирают приборами, которые называются батометрами. Они представляют собой бутылки, которые в зависимости от глубины потока опускают на штанге или с грузом (рис. 6.3.1). Здесь 1 – бутылка, 2 – воздухоотводящая трубка, 3 – воздухозаборная трубка, 4 – обойма, 5 – зажимной винт, 6 – хвост. Бутылку наполняют через водозаборную трубку, а воздух из неё удаляют через воздухоотводящую трубку.
Рис. 6.3.1. Батометр.
Принцип действия вакуумного батометра (рис. 6.3.2) основан на всасывании воды с наносами через заборный наконечник 1 и шланг 3 в вакуумную камеру 5 с помощью насоса 8. В камере создаётся разрежение, обеспечивающее всасывание воды со скоростью, близкой к местной скорости течения воды u.
В зависимости от глубины потока и скорости течения заборный наконечник 1 опускают в поток на штанге или на тросе с гидрометрическим грузом 11. Пробу сливают в бутыль через кран 10. Здесь 2 – держатель, 4 – трос, 6 – кран для выпуска воздуха, 7 – водомерное стекло, 9 – отверстие для выхода воздуха.
Взятие проб воды с одновременной автоматической записью температуры проводится с помощью батометра-батитермографа.
Прибор для измерения мутности по поглощению света экспресс-методом называется фотоэлектрическим мутномером (рис. 6.3.3).
Для фильтрования проб применяют беззольные фильтры. Фильтр предварительно высушивают и взвешивают на аналитических весах. Перед фильтрованием фильтр ополаскивают чистой водой. Фильтр с осевшими на нём наносами высушивается при температуре 105°С, после чего взвешивается на аналитических весах. Полученная величина за вычетом веса фильтра даёт вес наносов. Разделив вес наносов на объём пробы, получают относительную мутностьρм.
Расход наносов представляет собой произведение расхода воды на относительную мутность. Единичный расход взвешенных наносов в точке равен uρм.
Рис. 6.3.2. Вакуумный батометр.

Рис. 6.3.3. Фотоэлектрический мутномер.
Строим эпюры распределения uρм по глубине для скоростных вертикалей (рис. 6.3.4). Площади эпюр представляют собой удельные расходы взвешенных наносов на вертикалях gв. Строим кривую их распределения по ширине потока. Делением gв на h получаем средние единичные расходы наносов на вертикалях (uρм)в, строим кривую их распределения по ширине потока. Вычисляем расходы наносов на всех вертикалях gв = (uρм)вh. Площадь эпюры gв численно равна расходу взвешенных наносов Gн. Площадь фигуры под эпюрой gв равна массовому расходу взвешенных наносов Gв [г/с], Площадь фигуры под эпюрой gд равна массовому расходу донных наносов Gд [г/с].
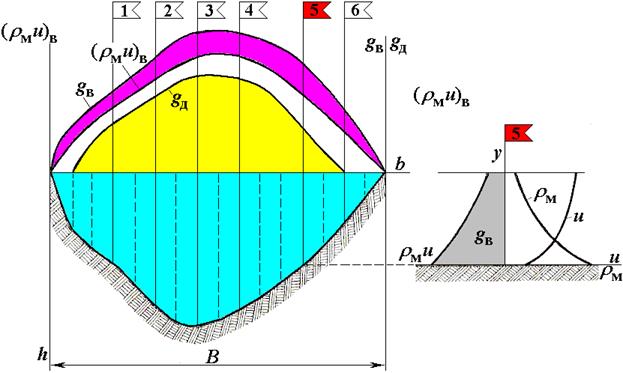
Рис. 6.3.4. Эпюры местной скорости течения u, местной мутности ρм [г/м3], расхода наносов в точке uρм [г/(см2·с)], расхода взвешенных наносов на вертикали  [г/(м·с)], расхода донных наносов на вертикали gд [г/(м·с)].
[г/(м·с)], расхода донных наносов на вертикали gд [г/(м·с)].
Для улавливания песчаных, влекомых по дну наносов пользуются батометром «Дон» (рис. 6.3.5), а для более крупных – гравелистых и галечных – батометром-сеткой (рис. 6.3.6). Батометр «Дон» состоит из ловушки и кожуха, а ловушка – из лотка 1, в который вкладывается рамка 2 с перегородками. Кожух 3 представляет собой коробку с дверцей 4. Дверца закрывает входное отверстие, когда батометр поднимают, а когда он находится на дне, пружина открывает дверцу. Батометр-сетка имеет ячейки диаметром, соответствующим наименьшему размеру улавливаемых наносов.
Рис. 6.3.5. Батометр для улавливания влекомых по дну песчаных наносов.
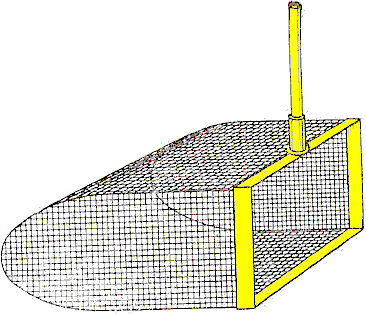
Рис. 6.3.6. Батометр для улавливания влекомых по дну гравелистых и галечных наносов.
§
ТЕМА 7.1. Расчётные гидрографы полноводий и паводков
При катастрофических паводках затапливаются населённые пункты, иногда имеют место аварии и даже разрушения плотин, мостов и других гидротехнических сооружений (рис. 7.1.1). При 1%-ной обеспеченности (вероятности превышения) максимальный расход равен или больше расчётной величины 1 раз в 100 лет, а при 0,1% – 1 раз в 1000 лет. Максимальный расход при определённом значении обеспеченности для рек, оборудованных гидрологическими постами, рассчитывается методами математической статистики по результатам многолетних наблюдений. При отсутствии или недостатке наблюдений расчёт основывается на площади водосбора, рельефе местности, многолетних данных об осадках и интенсивности снеготаяния.
Применяя в гидрологических расчётах методы математической статистики, необходимо понимать их смысл. Если расход 1%-ной вероятности превышения был 1 раз в 100 лет, то это еще не значит, что он не повторится в том же столетии второй раз. Так, на Дунае в 1897 и 1899 гг. прошли два катастрофических паводка 1%-ной обеспеченностью. В течение же очень длительного периода окажется, что максимальный расход 1%-ной обеспеченности повторяется в среднем только 1 раз в 100 лет, а за 500 лет – 5 раз и т. д. На Днепре у Киева максимальный расход 23 тыс. м³/с наблюдался в 1931 г. Его обеспеченность 0,4–1,0%.

Рис. 7.1.1. Повреждение моста при катастрофическом паводке.
Выбор обеспеченности максимального расхода обосновывается экономическими расчётами и соображениями безаварийной работы проектируемых сооружений. С уменьшением обеспеченности возрастает величина максимального расхода и размеры сооружения, а соответственно и стоимость его. Увеличение же расчётной обеспеченности максимального расхода приводит к снижению стоимости сооружения, но зато повышается вероятность его повреждения. Расчётная обеспеченность максимальных расходов зависит от класса капитальности сооружений.
Гидроэлектростанции мощностью > 1.000 МВт – I класс капитальности – обеспеченность 0,01.
Гидроэлектростанции мощностью 301 – 1.000 МВт – II класс капитальности – обеспеченность 0,1.
Гидроэлектростанции мощностью 51 – 300 МВт – III класс капитальности – обеспеченность 0,5.
Гидроэлектростанции мощностью 50 МВт и менее – IV класс капитальности – обеспеченность 1.
Рассмотрим схему формирования расхода на склоне, имеющем уклон в сторону дороги. На рис. 7.1.2 1 – трасса дороги (расчётный створ), 2, 3, 4 – изохроны (линии, к которым вода от удалённых участков добегает одновременно). Допустим следующие упрощения: 1) площадь водосборного бассейна F – прямоугольник со сторонами na и b; 2) склон в пределах всей площади водосбора имеет постоянный уклон i0 в сторону дороги и остальные характеристики поверхности: шероховатость, растительность, тип грунта, испарения и т. д.; 3) предыдущим дождём целиком заполнены все неровности микрорельефа и грунт насыщен водой; 4) дождь, формирующий сток, начинает выпадать и заканчивается одновременно на всей площади водостока.
Перечисленные характеристики должны обеспечить равные по всему водосборному бассейну условия водоотдачи сразу после начала выпадения дождя и условия стекания по склону. Интенсивность водоотдачи h – слой, образующий на данной площади сток за время Δt. Разобьём всю площадь водосбора F на n прямоугольников с равной площадью f и такой ширины a, чтобы можно было допустить, что вода со всех точек каждой полоски достигает расчётного створа (дороги) одновременно, например с первой f1 – за время Δt, со второй f2 – за время 2Δt и т. д. Время, в течение которого к расчётному створу начнёт поступать вода с самой отдалённой точки рассматриваемой площади бассейна, называют временем добегания 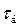 . Для площадки f1 время добегания Δt, для f2 – 2Δt, для всего водосборного бассейна время добегания
. Для площадки f1 время добегания Δt, для f2 – 2Δt, для всего водосборного бассейна время добегания 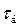 равно времени добегания с самой отдалённой площадки.
равно времени добегания с самой отдалённой площадки.
Границы 2, 3, 4 площадок f1, f2, f3 являются одновременно линиями равных времён добегания; такие линии называют изохронами. График поступления воды или изменения расхода во времени в створе дороги называют гидрографом паводка (рис. 7.1.3). Для бассейна, состоящего из трёх элементарных площадок f1, f2 и f3 (рис. 7.1.3а) через интервал времени Δt после начала выпадения дождя к расчётному створу придёт расход Qfтолько с части водосбора площадью f1. Через интервал 2Δt он увеличится до Q2f = 2Qf, через 3Δt достигнет QF = 3Qf. Время, в течение которого вода поступает на водосбор, называют временем водоотдачиТв. Если время водоотдачи Тв больше времени добегания  , то начиная с момента 3Δt от начала выпадения дождя, т. е. когда вода будет поступать в расчётный створ со всего водосбора F, расход QF = 3Qfбудет сохраняться постоянным. С окончанием дождя расход начнёт убывать. Если площадь F водосборного бассейна делить не на три, а на всё большее число полосок всё меньшей ширины, то ступенчатая часть гидрографа перейдёт в наклонные прямые, а сам гидрограф станет трапецией (рис. 7.1.3б). Здесь tп – время подъёма паводка, tн – время неизменного расхода, tсп – время спада.
, то начиная с момента 3Δt от начала выпадения дождя, т. е. когда вода будет поступать в расчётный створ со всего водосбора F, расход QF = 3Qfбудет сохраняться постоянным. С окончанием дождя расход начнёт убывать. Если площадь F водосборного бассейна делить не на три, а на всё большее число полосок всё меньшей ширины, то ступенчатая часть гидрографа перейдёт в наклонные прямые, а сам гидрограф станет трапецией (рис. 7.1.3б). Здесь tп – время подъёма паводка, tн – время неизменного расхода, tсп – время спада.

Рис. 7.1.2. Схема формирования расхода дождевых вод на склоне.
Продолжительность паводка Tп слагается из времени водоотдачи и времени добегания: Tп = Тв 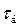 .
.
В действительности водосборный бассейн имеет неправильную форму (рис. 7.1.4а), рельеф, растительность, грунты различны на разных участках бассейна; начало и окончание дождя, его интенсивность также не везде одинаковы. В результате гидрограф трансформируется в фигуру типа треугольника (рис. 7.1.4б).
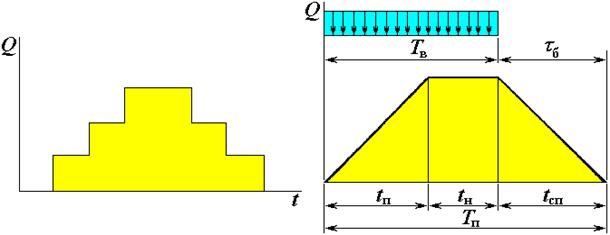
а б
Рис. 7.1.3. Гидрографы паводка: а – ступенчатый, б – трапецеидальный.
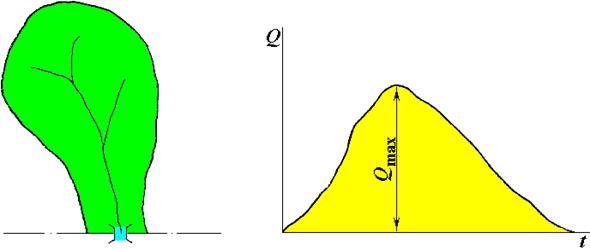
а б
Рис. 7.1.4. Водосборный бассейн (а) и его гидрограф (б).
Пример гидравлического расчёта нагорной канавы (рис. 7.1.5) на ливневый сток.
Исходные данные: район Донецка; поверхность и вид грунта водосборной площади – задернованная глина (для такой поверхности из табл. 7.1.1 коэффициент шероховатости 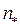 = 0,04; из табл. 7.1.2 коэффициент стока ψ = 0,20); средний уклон водосбора в направлении стока дождевых вод
= 0,04; из табл. 7.1.2 коэффициент стока ψ = 0,20); средний уклон водосбора в направлении стока дождевых вод 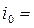 0,04; длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
0,04; длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
Требуется выполнить гидравлический расчет канавы в сечении, проходящем через точку В на рис. 7.1.6.
Расчёт производится в соответствии с рекомендациями инструкции «Руководство по проектированию водоотвода и дренажа на летных полях аэродромов» [13].

Рис. 7.1.5. Нагорная канава трапецеидального сечения.
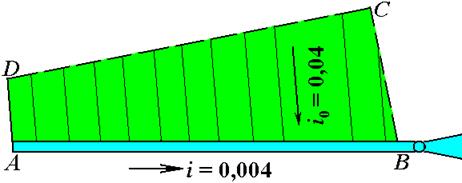
Рис. 7.1.6. Водосборный бассейн нагорной канавы.
Таблица 7.1.1. Коэффициент шероховатости поверхностей.
Таблица 7.1.2. Коэффициент стока поверхностей.
| Вид поверхности | Коэффициент стока ψ |
| Кровли и асфальтобетонные покрытия Брусчатые мостовые Булыжные мостовые Щебёночные покрытия Гравийные садово-парковые дорожки Грунтовые поверхности (спланированные) Газоны | 0,95 0,6 0,45 0,4 0,3 0,2 0,1 |
Решение. По карте находим для района Донецка интенсивность дождя продолжительностью 20 мин с вероятным периодом превышения один раз в год 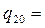 88 л/с/га (рис. 7.1.7). По табл. 7.1.3 находим для востока Украины среднее количество дождей за год
88 л/с/га (рис. 7.1.7). По табл. 7.1.3 находим для востока Украины среднее количество дождей за год 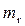 = 60, показатель степени γ = 1,82, для периода однократного превышения расчетной интенсивности дождя P ≥ 1 год показатель степени n = 0,67.
= 60, показатель степени γ = 1,82, для периода однократного превышения расчетной интенсивности дождя P ≥ 1 год показатель степени n = 0,67.
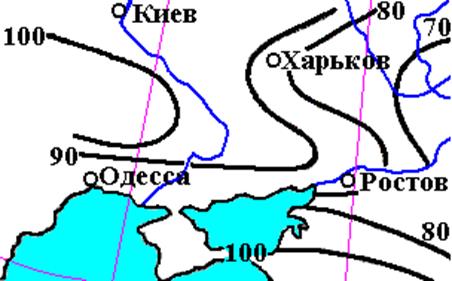
Рис. 7.1.7. Интенсивность дождя продолжительностью 20 мин с вероятным периодом превышения один раз в год 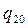 (л/с/га).
(л/с/га).
Таблица 7.1.3. Коэффициенты для определения расчётной продолжительности дождя.
| Район | Значение n при | mr | g | |
| Р ³ 1 | Р < 1 | |||
| Равнинные области Украины | 0,71 | 0,64 | 1,54 | |
| Восток Украины, Южный Крым | 0,67 | 0,57 | 1,82 |
Параметр расчётной продолжительности дождя
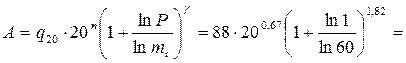 655 л/с/га =
655 л/с/га =
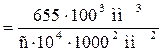 = 0,0655 мм/с = 3,93 мм/мин.
= 0,0655 мм/с = 3,93 мм/мин.
Из табл. 7.1.4 минимальная мгновенная стокообразующая интенсивность дождя, принимаемая равной интенсивности впитывания, iст = U* =0,06 мм/мин. Продолжительность стокообразования
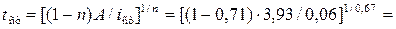 98,2 мин.
98,2 мин.
Длина склона, участвующего в стоке сечения в точке B (равная пути движения воды за время стекания; с более удалённых участков вода не доходит, так как впитывается в грунт),
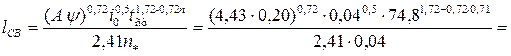 509 м.
509 м.
Таблица 7.1.4. Интенсивность впитывания различными поверхностями.
| Грунты и почвы | Интенсивность впитывания U*, мм/мин |
| Глины, солонцы суглинистые | 0,06 |
| Суглинки, суглинистые черноземы, сероземы глинистые | 0,08 |
| Каштановые почвы, чернозем обычный, солонцы супесчаные | 0,15 |
| Супеси с примесью гумуса в верхних слоях, задернованные, супеси, серолесные почвы | 0,20 |
| Чистые открытые супеси | 0,33 |
| Чистые открытые пески | 0,50 |
Из точек D и C вода приходит в точку B одновременно. Поскольку длина стока lDA определяется как путь движения воды за время 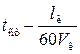 , то длина lDAоказывается зависимой от скорости течения воды по канаве
, то длина lDAоказывается зависимой от скорости течения воды по канаве 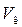 , которая в свою очередь зависит от геометрических размеров канавы и глубины потока
, которая в свою очередь зависит от геометрических размеров канавы и глубины потока 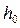 . Кроме того, от глубины потека
. Кроме того, от глубины потека 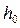 существенно зависит пропускная способность канавы Q0 которая в идеальном случае должна быть равна расчетному расходу Qр, зависящему от площади одновременного стока Fст, т.е. и от величины lDA. Поэтому величину lDAи связанную с ней глубину потока h0 целесообразно определять методом подбора. Будем считать ширину канавы по дну величиной постоянной, равной b = 0,4 м, а глубину потока будем подбирать такой, чтобы пропускная способность канавы Q0 равнялась расчетному расходу Q.
существенно зависит пропускная способность канавы Q0 которая в идеальном случае должна быть равна расчетному расходу Qр, зависящему от площади одновременного стока Fст, т.е. и от величины lDA. Поэтому величину lDAи связанную с ней глубину потока h0 целесообразно определять методом подбора. Будем считать ширину канавы по дну величиной постоянной, равной b = 0,4 м, а глубину потока будем подбирать такой, чтобы пропускная способность канавы Q0 равнялась расчетному расходу Q.
Скорость течения воды определяется по формуле
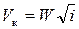 ,
,
где
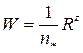 ;
;  ;
; 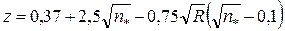 .
.
Результаты расчётов приведены в табл. 7.1.5.
Таблица 7.1.5. Расчёт нагорной канавы на сток дождевых вод.
 , м , м | 0,40 | 0,50 | 0,424 |
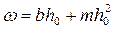 , м2 , м2 | 0,40 | 0,58 | 0,44 |
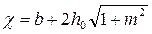 , м , м | 1,84 | 2,20 | 1,93 |
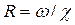 , м , м | 0,22 | 0,26 | 0,23 |
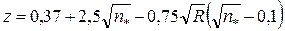 | 0,84 | 1,02 | 0,96 |
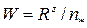 , м/с , м/с | 7,01 | 6,33 | 6,10 |
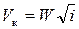 , м/с , м/с | 0,44 | 0,52 | 0,46 |
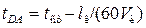 , мин , мин | 52,9 | 59,5 | 54,7 |
 , м , м | 47,4 | 54,8 | 49,4 |
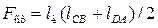 , га , га | 33,4 | 33,8 | 33,5 |
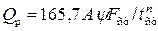 , л/с , л/с | |||
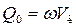 , л/с , л/с |
Таким образом, расход Q = 202 л/с, глубина потока 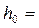 0,424 м, ширина канавы по дну b = 0,4 м, длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5, скорость потока в канаве Vк = 0,46 м/с.
0,424 м, ширина канавы по дну b = 0,4 м, длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5, скорость потока в канаве Vк = 0,46 м/с.
Полная глубина канавы с учётом превышения бровки канала над расчётным уровнем воды (рис. 7.1.8) hк = h0 0,25 = 0,42 0,25 ≈ 0,67 м.
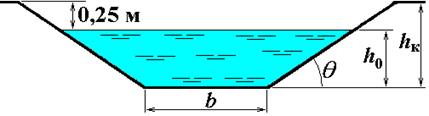
Рис. 7.1.8. Поперечное сечение канавы.
Так как согласно табл. 7.1.6 допустимая скорость для глины составляет 1,2·0,85 = 1,02 м/с, что больше Vк = 0,46 м/с, то укрепления откосов и дна канавы не требуется.
Таблица 7.1.6. Максимальная неразмывающая скорость.
| Грунт лотка | Максимальная скорость, м/с | Вид укрепления откосов канав | Максимальная скорость, м/с |
| Мелкозернистый и среднезернистый песок, супеси | 0,4 | Одерновка плашмя | 1,0 |
| Одерновка в стенку | 1,6 | ||
| Крупнозернистый песок | 0,8 | Мощение одиночное | 2,0 |
| Суглинок | 0,7 | Мощение двойное | 3,5 |
| Суглинок тяжелый | 1,0 | Грунт, обработанный вяжущими | 5,0 |
| Глина | 1,2 | Бетонные плиты | 8,0 |
Примечание: Значения скоростей даны для глубины потока от 0,4 до 1,0 м. При глубине потока менее 0,4 м табличные значения скоростей принимаются с поправочным коэффициентом 0,85, а при глубине более 1 м – с коэффициентом 1,25.
Пример вычисления максимального расхода талых вод 1%-ной обеспеченности при отсутствии наблюдений.
Исходные данные: балка Сухая Маячка (бассейн Днепра) в Полтавской области; площадь водосбора F = 117 км²; уклон балки i = 1,4‰; длина L = 23,3 км; площадь лесов fл = 14%. Озёр на водосборе нет (δ1 = 1,0), болот нет (fб = 0). Обеспеченность p% = 1.
Решение. По карте рис. 7.1.9 норма весеннего стока (сплошная линия) уср = 40 мм, коэффициент изменчивости (штрихпунктирная линия) Cv = 0,65. По табл. 7.1.7 модульный коэффициент k1% = f(Cv, p%) = 3,09. По табл. 7.1.8 для Украины коэффициент редукции n = 0,25; коэффициент дружности половодья для категории рельефа II (холмистые возвышенности чередуются с понижениями между ними) k0 = 0,017. По табл. 7.1.9 коэффициент, учитывающий неравенство статистических и максимальных параметров, μ = 1,0. Сток при 1%-ной обеспеченности у1% = k1%уср = 3,09∙40 = 124 мм.
Коэффициент, учитывающий залесённость и заболоченность,
δ = 1 – 0,8·lg(0,5fл 0,1fб 1) = 1 – 0,8·lg(0,5∙14 0,1∙0,0 1) = 0,82.
Максимальный расход талых вод 1%-ной обеспеченности
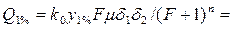
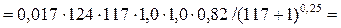 61,3 м3/с.
61,3 м3/с.
Таким образом, примерно 1 раз в 100 лет расход талых вод превысит 61,3 м³/с.
Рис. 7.1.9. Норма весеннего стока (сплошная линия) уср (мм) и коэффициент изменчивости Cv (штрихпунктирная линия).
Таблица 7.1.7. Модульный коэффициент k1%.
| Коэффициент изменчивости Cv | Обеспеченность p% | ||||
| 0,1 | |||||
| 0,60 | 3,89 | 2,89 | 2,39 | 2,15 | 1,80 |
| 0,65 | 4,22 | 3,09 | 2,52 | 2,25 | 1,87 |
Таблица 7.1.8. Коэффициент дружности половодья k0.
| Район | Коэффициент редукции n | Коэффициент дружности половодья k0 для категорий рельефа | ||
| I | II | III | ||
| Украина | 0,25 | 0,030 | 0,017 | 0,012 |
| Северный Кавказ | 0,25 | 0,030 | 0,025 | 0,015 |
Категории рельефа: I категория – бассейны рек расположены в пределах холмистых и платообразных возвышенностей (Среднерусская и др.). II категория – холмистые возвышенности чередуются с понижениями между ними. III категория – плоские низменности (Приднепровская и др.).
Таблица 7.1.9. Коэффициент μ, учитывающий неравенство статистических и максимальных параметров.
| Природная зона | μ при вероятности превышения, % | ||||
| 0,1 | |||||
| Лесостепная и степная зоны: | |||||
| При F ≥ 200 км2 При F < 200 км2 | 1,05 1,10 | 1,00 1,00 | 0,96 0,93 | 0,94 0,87 | 0,92 0,79 |
Пример гидравлического расчёта нагорной канавы на сток талых вод.
Исходные данные: район Донецка; водосборная площадь F = 75 га (задернованный суглинок). Озёра и болота отсутствуют, лес отсутствует. Продольный уклон канавы i = 0,004.
Решение. Максимальная интенсивность снеготаяния, определяемая по карте рис. 7.1.10, A = 1,3 мм/ч.
Рис. 7.1.10. Максимальная интенсивность снеготаяния A (мм/ч).
С увеличением площади меняется интенсивность снеготаяния на отдельных участках бассейна, возрастает неодновременность добегания воды к расчётному створу со всей площади водосбора. Коэффициент редукции (уменьшения) максимального стока талых вод
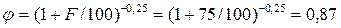 .
.
Коэффициент снижения расходов за счёт аккумуляции воды в болотах и озёрах на водосборе
δ’ = 1 − 0,6∙lg(Fo 0,2Fб 1) = 1 − 0,6∙lg(0 0,2∙0 1) = 1,
где Fo и Fб − доля в общей площади водосбора озёр и болот соответственно.
Коэффициент снижения расходов при наличии леса на водосборе
δ” = 1 − γlg(1 Fл) = 1 − 0,25∙lg(1 0) = 1,
где Fл − доля лесов в общей площади водосбора, γ – коэффициент, равный для лесов на песчаных и супесчаных почвах 0,35 – 0,40 и для лесов на суглинистых почвах – 0,25 – 0,30.
Расчётный расход талых вод, поступающих в канаву:
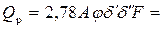 2,78·1,3∙1,0∙1,0∙1,0∙75 = 236 л/с,
2,78·1,3∙1,0∙1,0∙1,0∙75 = 236 л/с,
В расчётном сечении (рис. 7.1.6) задаёмся параметрами канавы: b = 0,4 м; коэффициент заложения откосов m = 1,5. Из табл. 7.1.1 коэффициент шероховатости грунтовой поверхности без дернового покрова 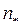 = 0,025. Решаем задачу методом подбора. Подбираем такое значение глубины потока в канаве, при котором расход воды в канаве равен расчётному расходу талых вод, поступающих в канаву. Площадь живого сечения
= 0,025. Решаем задачу методом подбора. Подбираем такое значение глубины потока в канаве, при котором расход воды в канаве равен расчётному расходу талых вод, поступающих в канаву. Площадь живого сечения 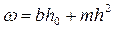 , смоченный периметр
, смоченный периметр 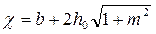 , гидравлический радиус
, гидравлический радиус 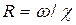 . Показатель степени в формуле Павловского
. Показатель степени в формуле Павловского 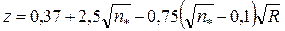 . Скоростная характеристика
. Скоростная характеристика 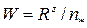 . Скорость воды в канаве
. Скорость воды в канаве 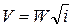 . Пропускная способность канавы в расчётном сечении
. Пропускная способность канавы в расчётном сечении 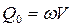 .
.
Результаты расчётов приведены в табл. 7.1.10.
Таблица 7.1.10. Расчёт нагорной канавы на сток талых вод.
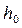 , м , м | 0,30 | 0,40 | 0,346 |
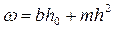 , м2 , м2 | 0,26 | 0,40 | 0,32 |
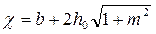 , м , м | 1,48 | 1,84 | 1,65 |
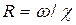 , м , м | 0,17 | 0,22 | 0,19 |
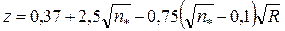 | 0,75 | 0,74 | 0,75 |
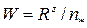 , м/с , м/с | 10,6 | 13,0 | 11,5 |
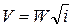 , м/с , м/с | 0,68 | 0,81 | 0,74 |
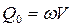 , л/с , л/с |
Полная глубина канавы с учётом запаса глубины 0,25 м равна
hк = h0 0,25 = 0,35 0,25 = 0,60 м.
Так как согласно табл. 7.1.6 допустимая скорость для суглинка составляет 0,7·0,85 = 0,60 м/с, что меньше V = 0,74 м/с, то требуется укрепления откосов и дна канавы одерновкой плашмя. При этом максимально допустимая (неразмывающая) скорость движения воды возрастает до 1,0·0,85 = 0,85 м/с.
ТЕМА 7.2. Малые мосты
К малым мостам (рис. 7.2.1) относятся мосты, полная длина которых не превышает 25 м. Они являются одним из видов водопропускных сооружений на автомобильных и железных дорогах при пересечении ими сухих логов и русел периодически действующих водотоков, оросительных каналов и т. п. Согласно действующим типовым проектам малые мосты имеют стандартные отверстия (расстояние в свету между устоями или опорами): 2; 3; 4; 5; 6; 7,5; 10; 12,5 и 20 м.

Рис. 7.2.1. Малый мост.
Форма устоев моста (рис. 7.2.2а) определяет коэффициент расхода m: облегчённые (а) m = 0,32; с откосными крыльями (б) m = 0,35; с обратными стенками(в) m = 0,32…0,36 (большие значения для больших напоров); эстакадные с конусами (г) m = 0,32.
Различают свободное (незатопленное) и несвободное (затопленное) протекание воды в подмостовом русле. Условие затопления: hнб ≤ NH, где hнб – глубина потока в нижнем бьефе, H – напор перед мостом. Критерий затопления принимает значения N = 0,78…0,84 в зависимости от коэффициента расхода m: N = 1,32 – 1,5m. При hn < NH имеем незатопленный водослив с широким порогом; при hn > NH – затопленный водослив.

Рис. 7.2.2. Формы устоев моста: облегчённые (а), с откосными крыльями (б), с обратными стенками(в), эстакадные с конусами (г).
Рис. 7.2.3а. В конце входного участка устанавливается глубина 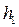 меньше критической
меньше критической 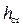 и меньше нормальной глубины в подмостовом русле
и меньше нормальной глубины в подмостовом русле  . Незатопленный водослив. При уклоне русла меньшем критического
. Незатопленный водослив. При уклоне русла меньшем критического 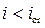 наблюдается гидравлический прыжок после входного участка. Здесь
наблюдается гидравлический прыжок после входного участка. Здесь 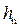 – бытовая (нормальная) глубина нестеснённого потока.
– бытовая (нормальная) глубина нестеснённого потока.
Рис. 7.2.3б. В конце входного участка устанавливается глубина 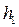 меньше критической, но больше нормальной глубины в подмостовом русле
меньше критической, но больше нормальной глубины в подмостовом русле 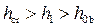 . За входным участком глубины уменьшаются. Незатопленный водослив.
. За входным участком глубины уменьшаются. Незатопленный водослив.
Рис. 7.2.3в. В конце входного участка устанавливается глубина больше критической, но меньше нормальной глубины в подмостовом русле  . Затопленный водослив.
. Затопленный водослив.
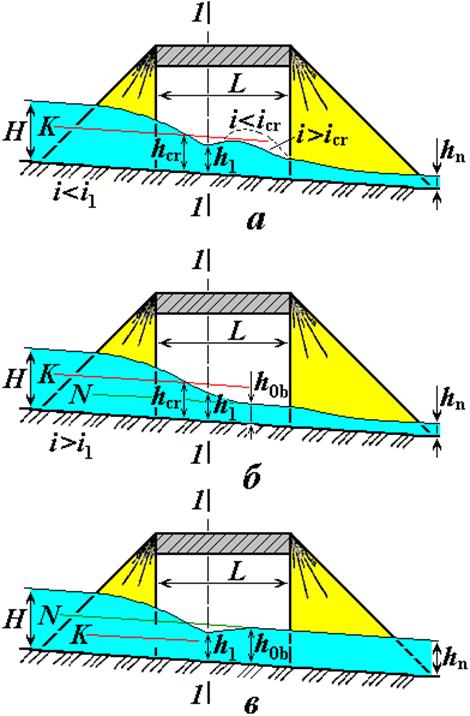
Рис. 7.2.3. Водослив в подмостовом русле: а – незатопленный с гидравлическим прыжком, б – незатопленный без прыжка, в – затопленный.
Как в случае незатопленных, так и в случае затопленных подмостовых водосливов пропускная способность малых мостов определяется по общей формуле водослива (4.6.20), откуда необходимое отверстие моста
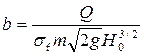 , (7.2.1)
, (7.2.1)
где m – коэффициент расхода, который в зависимости от формы устоев моста принимает значение от 0,32 до 0,36 [6, с. 159, табл. 11.1]; 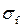 – коэффициент затопления, зависящий от коэффициента расхода m и от степени подтопления
– коэффициент затопления, зависящий от коэффициента расхода m и от степени подтопления 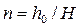 [6, с. 161, табл. 11.5]. Для незатопленных водосливов
[6, с. 161, табл. 11.5]. Для незатопленных водосливов 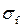 = 1.
= 1.
Отверстие малого моста всегда меньше ширины потока (при расчётном расходе), и в результате этого часть протекающей воды с водосборного бассейна задерживается перед сооружением (рис. 7.2.4), образуя некоторый объём аккумулированной (временно накопившейся) воды Wак, который может составлять значительную часть общего объёма стока W. Учёт временного накопления воды перед сооружением с образованием пруда позволяет пропустить этот же объём стока за более продолжительный период. В связи с этим сбросный расход, по которому определяется отверстие моста, всегда меньше максимального расчётного.

Рис. 7.2.4. Аккумуляция воды перед мостом.
Пример 7.2.1. Графоаналитическим методом рассчитать отверстие малого моста с облегчёнными устоями с учётом аккумуляции (накопления) в логе перед мостом. Расход Q = 30 м³/с; объём стока W = 80 тыс. м³; уклон дна лога iл = 0,005; уклоны склонов лога ic1 = ic2 = 0,007. Напор перед мостом H ≤ 1,7 м, бытовая глубина воды в логе h0 = 0,53 м.
Решение.
1. Для мостов облегчённой системы (рис. 7.2.2а и 7.2.4) коэффициент расхода m = 0,32 [6, с. 159, табл. 11.1] и критерий затопления N = 0,84 [6, с. 160, табл. 11.4]. Коэффициент формы лога
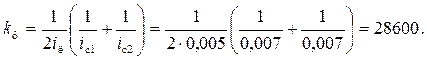
2. Назначаем ряд величин H и вычисляем объём аккумулированной воды Wак = kфH³/3, степень аккумуляции Wак/W, коэффициент аккумуляции φак = 1 – Wак/W, сбросный расход Qсб = φакQmax. Результаты расчётов заносим в табл. 7.2.1.
Таблица 7.2.1. Расчёт сбросного расхода аккумуляции.
| Параметры | Напор перед мостом Н, м | |||
| 1,25 | 1,5 | 1,75 | ||
| Объём аккумулированной воды Wак = kфH3/3, тыс. м3 | 9,55 | 18,6 | 32,5 | 51,5 |
| Степень аккумуляции Wак/W | 0,12 | 0,23 | 0,41 | 0,65 |
| Коэффициент аккумуляции φак = 1 – Wак/W | 0,88 | 0,77 | 0,59 | 0,35 |
| Сбросный расход Qсб = φакQmax, м3/с | 26,4 | 23,0 | 17,7 | 10,5 |
3. Полученную зависимость 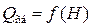 наносим на график пропускной способности малых мостов [6, с. 165, рис. 11.4]. Точки пересечения функции
наносим на график пропускной способности малых мостов [6, с. 165, рис. 11.4]. Точки пересечения функции 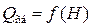 (рис. 7.2.5) с учётом нормативных требований, что
(рис. 7.2.5) с учётом нормативных требований, что 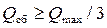 = 10 м³/с, определяет решения по расчёту отверстия моста, приведенные в табл. 7.2.2.
= 10 м³/с, определяет решения по расчёту отверстия моста, приведенные в табл. 7.2.2.
Таблица 7.2.2. Расчёт отверстия моста.
| Отверстие моста b, м | |||||
| Напор перед мостом H, м | 1,67 | 1,62 | 1,54 | 1,42 | 1,32 |
Сбросный расход  , м3/с , м3/с | 12,5 | 14,6 | 16,4 | 19,2 | 21,5 |
4. С учётом того, что по условию задачи напор перед мостом  м, в соответствии с выполненными расчётами выбираем вариант b = 4 м при Н = 1,67 м и
м, в соответствии с выполненными расчётами выбираем вариант b = 4 м при Н = 1,67 м и 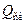 = 12,5 м3/с.
= 12,5 м3/с.
5. При коэффициенте расхода m = 0,32 коэффициент k = 0,45 [6, с. 160, табл. 11.4]. Глубина потока в расчётном сечении (рис. 7.2.3а) 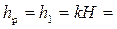 0,75 м.
0,75 м.

Рис. 7.2.5. Пропускная способность малых мостов.
6. Скорость в расчётном сечении подмостового русла
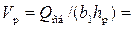 4,1 м/с.
4,1 м/с.
7. Исходя из значений максимальной допустимой (неразмывающей) скорости [6, с. 95, табл. 7.12], устанавливаем, что при Vp = 4,1 м и h0 = 0,75 м подмостовое русло может быть укреплено мощением из камня размером 25 см на слое щебня в 10 см или бетонными плитами.
§
Применение труб (рис. 7.3.1) предпочтительнее, чем малых мостов. Однако трубы не рекомендуется применять: на постоянно действующих водотоках с возможным ледоходом; водотоках, где возможно образование наледей; переходах через селевые потоки. В настоящее время чаще всего применяются водопропускные трубы круглого сечения. По числу отверстий трубы бывают одноочковые, двухочковые, трёхочковые и многоочковые. Согласно действующим типовым проектам дорожные водопропускные трубы имеют стандартные отверстия с внутренним диаметром 0,75; 1; 1,25; 1,5 и 2 м.

Рис. 7.3.1. Водопропускные дорожные трубы.
Безнапорный режим протекания потока (рис. 7.3.2а) характеризуется наличием свободной поверхности потока на всём протяжении трубы. Труба работает в безнапорном режиме, если H ≤ 1,2hтр.
Полунапорный режим протекания потока в трубе (рис. 7.3.2б) имеет два характерных участка: участок на входе и основной. Входной участок характеризуется затопленным входом в трубу, где поток соприкасается по всему периметру со стенками трубы. Входной участок заканчивается сжатым сечением с глубиной hc< hкр, затем поток протекает со свободной поверхностью. Условием существования полунапорного режима является критерий H > 1,2hтр.
Напорный режим (рис. 7.3.2в) характеризуется тем, что всё поперечное сечение трубы по всей длине полностью заполнено водой. При напорном режиме трубы обладают наибольшей пропускной способностью. Напорный режим имеет место при одновременном выполнении трёх условий:
1) обтекаемый входной оголовок;
2) H > 1,2hтр;
3) iтр < if, где iтр – уклон дна трубы,  – уклон трения,
– уклон трения, 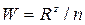 – скоростная характеристика
– скоростная характеристика
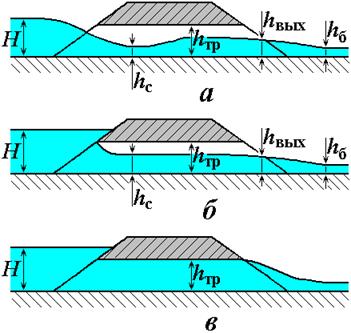
Рис. 7.3.2. Режимы протекания: а – безнапорный, б – полунапорный, в – напорный.
Наименьшая допустимая высота насыпи Нmin над трубами устанавливается расчётом в соответствии с приведенными ниже формулами:
а) по засыпке грунта при безнапорном режиме (рис. 7.3.3а) Hmin = hтр hкон hзас;
б) при полунапорном и напорном режимах (рис. 7.3.3б) Hmin = Н D.
Здесь hтр – высота (диаметр) трубы; hкон – толщина стенки трубы; hзас – высота засыпки (не менее 0,5 м); Н – напор перед трубой; D – запас над уровнем подпёртых вод, принимаемый для труб малых отверстий не менее 0,5 м, а для труб отверстием 2 и больше – не менее 1 м.
На режим работы трубы оказывают особое влияние входные, а также выходные оголовки, которые предназначены для сопряжения трубы с откосами земляного полотна. Входные оголовки подразделяются на обтекаемые и необтекаемые.
Обтекаемые оголовки характеризуются или повышенным входным звеном, или конически сходящимся звеном (рис. 7.3.4). К необтекаемым оголовкам (рис. 7.3.5) относятся раструбные (а), портальные (б) и воротниковые (в).
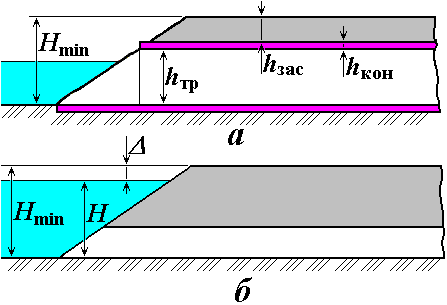
Рис. 7.3.3. Минимальная высота насыпи: а – при безнапорном режиме, б – при полунапорном и напорном режимах.

Рис. 7.3.4. Обтекаемый оголовок с повышенным входным звеном.
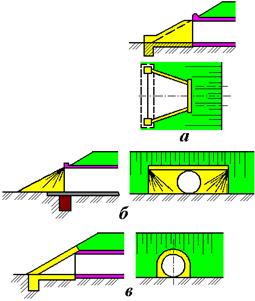
Рис. 7.3.5. Необтекаемые оголовки: а – раструбные, б – портальные, в – воротниковые.
Обтекаемые оголовки хотя и обладают большей пропускной способностью, но уступают по трудоёмкости изготовления необтекаемым, среди которых несколько большая пропускная способность у раструбных оголовков (рис. 7.3.6).

Рис. 7.3.6. Необтекаемый раструбной оголовок.
Пример 7.3.1. Рассчитать круглую железобетонную трубу стандартного отверстия при коэффициенте шероховатости n = 0,014 для пропуска расхода Q = 9 м³/с, уклоне лога i = 0,02 в условиях безнапорного (при предельной степени наполнения 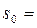 0,95), полунапорного и напорного режимов.
0,95), полунапорного и напорного режимов.
Решение.
Примем двухочковые трубы для расчётного расхода 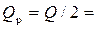 4,5 м³/с.
4,5 м³/с.
а) Безнапорный режим с обтекаемым оголовком. Из табл. 7.3.1 [6, c. 173, табл. 11.9] выбираем d = 2,00 м. При этом напор H = 1,53 м, скорость V = 2,8 м/с. Условие 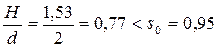 выполнено.
выполнено.
Расходная характеристика  31,8 м3/с. По табл. 7.3.2 [14, с. 287, приложение 14, фрагмент для d = 2 м и n = 0,014] для d = 2 м, n = 0,014 и
31,8 м3/с. По табл. 7.3.2 [14, с. 287, приложение 14, фрагмент для d = 2 м и n = 0,014] для d = 2 м, n = 0,014 и 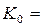 31,8 м3/с находим, что
31,8 м3/с находим, что 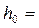 0,64 м. По той же таблице, полагая
0,64 м. По той же таблице, полагая 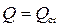 , устанавливаем, что
, устанавливаем, что 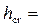 1,05 м. В связи с тем, что
1,05 м. В связи с тем, что 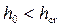 , поток находится в бурном состоянии и, следовательно, hвых = 0,7h0 = 0,7∙0,64 = 0,45 м и соответственно ωвых = 0,53 м2. Скорость протекания в расчётном сечении Vвых = Q/ωвых = 4,5/0,53 = 8,5 м/с. Такая неразмывающая скорость обеспечивается для монолитного бетонного лотка [14, с. 274, приложение 5].
, поток находится в бурном состоянии и, следовательно, hвых = 0,7h0 = 0,7∙0,64 = 0,45 м и соответственно ωвых = 0,53 м2. Скорость протекания в расчётном сечении Vвых = Q/ωвых = 4,5/0,53 = 8,5 м/с. Такая неразмывающая скорость обеспечивается для монолитного бетонного лотка [14, с. 274, приложение 5].
Таблица 7.3.1. Пропускная способность железобетонных труб.
| Q, м3/с | d = 1,25 м | d = 1,50 м | d = 2,00 м | |||||||||
| Тип входного оголовка (I – необтекаемый, II – обтекаемый) | ||||||||||||
| I | II | I | II | I | II | |||||||
| H | V | H | V | H | V | H | V | H | V | H | V | |
| 4,0 | 2,66 | 5,2 | 1,84 | 3,2 | 1,75 | 3,1 | 1,60 | 3,1 | 1,53 | 2,7 | 1,43 | 2,7 |
| 4,5 | 3,26 | 5,9 | 1,98 | 3,7 | 2,07 | 4,2 | 1,71 | 3,2 | 1,65 | 2,8 | 1,53 | 2,8 |
Таблица 7.3.2. Таблица для расчёта дорожных труб.
| h, м | ω, м2 | 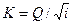 , м3/с , м3/с | hвых = 0,7h, м | ωвых, м2 | Qcr, м3/с |
| 0,60 | 0,79 | 28,0 | 0,42 | 0,48 | 1,6 |
| 0,70 | 0,98 | 37,5 | 0,49 | 0,60 | 2,1 |
| 1,00 | 1,57 | 71,2 | 0,70 | 0,98 | 4,2 |
| 1,06 | 1,69 | 78,5 | 0,74 | 1,07 | 4,6 |
б) Полунапорный режим с необтекаемым оголовком. Из табл. 7.3.1 выбираем d = 1,50 м. При этом напор H = 2,07 м, скорость V = 4,2 м/с. Критерий полунапорного режима H > 1,2d выполняется: H = 2,07 > 1,2d = 1,2∙1,5 = 1,8. Критерий напорного режима H > 1,4d не выполняется: H = 2,07 < 1,4d = 1,4∙1,5 = 2,1.
Расходная характеристика  31,8 м3/с. По таблице [14, с. 286, приложение 14] для d = 1,5 м, n = 0,014 и
31,8 м3/с. По таблице [14, с. 286, приложение 14] для d = 1,5 м, n = 0,014 и 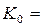 31,8 м3/с находим, что
31,8 м3/с находим, что 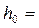 0,72 м. По той же таблице, полагая
0,72 м. По той же таблице, полагая 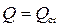 , устанавливаем, что
, устанавливаем, что  1,15 м. В связи с тем, что
1,15 м. В связи с тем, что 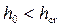 , поток находится в бурном состоянии и, следовательно, hвых = 0,7h0 = 0,7∙0,72 = 0,50 м и соответственно ωвых = 0,81 м2. Скорость протекания в расчётном сечении Vвых = Q/ωвых = 4,5/0,81 = 5,6 м/с. Такая неразмывающая скорость обеспечивается для бутовой кладки из средних пород [14, с. 274, приложение 5].
, поток находится в бурном состоянии и, следовательно, hвых = 0,7h0 = 0,7∙0,72 = 0,50 м и соответственно ωвых = 0,81 м2. Скорость протекания в расчётном сечении Vвых = Q/ωвых = 4,5/0,81 = 5,6 м/с. Такая неразмывающая скорость обеспечивается для бутовой кладки из средних пород [14, с. 274, приложение 5].
в) Напорный режим с обтекаемым оголовком. Из табл. 7.3.1 выбираем d = 1,25 м. При этом напор H = 1,98 м, скорость V = 3,7 м/с. Критерий напорного режима H > 1,4d выполняется: H = 1,98 > 1,4d = 1,4∙1,25 = 1,75.
Площадь живого сечения на выходе из трубы ωвых = 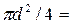 π∙1,252/4 = 1,23 м2, скорость потока Vвых = Q/ωвых = 4,5/1,23 = 3,67 м/с. Такая неразмывающая скорость обеспечивается мощением из рваного камня размером 20 см на слое щебня не менее 10 см [14, с. 274, приложение 5].
π∙1,252/4 = 1,23 м2, скорость потока Vвых = Q/ωвых = 4,5/1,23 = 3,67 м/с. Такая неразмывающая скорость обеспечивается мощением из рваного камня размером 20 см на слое щебня не менее 10 см [14, с. 274, приложение 5].
ТЕМА 7.4. Акведуки и дюкеры
Акведуки устраиваются при пересечениях канала с дорогами (рис. 7.4.1), с понижениями местности (рис. 7.4.2), с реками (рис. 7.4.3). Они представляют собой мосты–водоводы. На рис. 7.4.4 показан древнеримский акведук в Сеговии (Испания).

Рис. 7.4.1. Акведук на пересечении канала с дорогой.
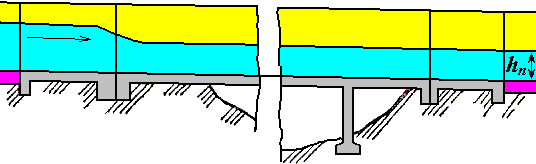
Рис. 7.4.2. Акведук на пересечении канала с понижением местности.
Отметка дна в акведуке у входа чаще всего принимается такая, как и в подводящем канале, или незначительно выше. Расчёт входного участка акведука производится по формуле подтопленного водослива с широким порогом
 , (7.4.1)
, (7.4.1)
где φ – коэффициент скорости (при плавном входе φ = 0,96…0,97, при неплавном входе φ = 0,90…0,95); b – ширина суженной части лотка; hn – глубина в суженной части акведука, которую берут приблизительно равной глубине в отводном канале; H – глубина воды в лотке до сужения.

Рис. 7.4.3. Акведук на пересечении канала с рекой.

Рис. 7.4.4. Древнеримский акведук.
Дюкерами называют напорные трубопроводы, устраиваемые при пересечении канала или водопровода с дорогами (на рис. 7.4.5 показан дюкер канала Северский Донец – Донбасс над железной дорогой, на рис. 7.4.6 – под дорогой), под реками (рис. 7.4.7), каналами и т. п.
Дюкеры следует проектировать согласно СНиП 2.04.03-85, переходы трубопроводов через железные и автомобильные дороги – согласно СНиП 2.04.02-84.

Рис. 7.4.5 Дюкер канала Северский Донец – Донбасс над железной дорогой.

Рис. 7.4.6. Дюкер под дорогой.
Диаметры труб дюкеров следует принимать не менее 150 мм.
Дюкеры при пересечении водоёмов и водотоков необходимо принимать не менее чем в две рабочие линии из стальных труб с усиленной антикоррозионной изоляцией, защищённой от механических повреждений. Каждая линия дюкера должна проверяться на пропуск расчётного расхода с учётом допустимого подпора.
При расходах сточных вод, не обеспечивающих расчётных незаиливающих скоростей (СНиП 2.04.03-85, п. 2.34), одну из двух линий надлежит принимать резервной (нерабочей).
При пересечении оврагов и суходолов допускается предусматривать дюкеры в одну линию.
При проектировании дюкеров необходимо принимать глубину заложения подводной части трубопровода от проектных отметок или возможного размыва дна водотока до верха трубы – не менее 0,5 м, в пределах фарватера на судоходных водных объектах – не менее 1 м.

Рис. 7.4.7. Прокладка дюкера по дну реки.
Гидравлический расчёт дюкеров производят так же, как напорных трубопроводов, принимая расход, равный расходу канала. Скорость течения принимают равной 1,5…4 м/с во избежание заиливания. Разность отметок уровней воды у входной и выходной частей дюкера составляет расчётный напор ΔH. Для равнинного рельефа этот напор должен быть минимальным. Обычно гидравлический расчёт дюкера сводится к определению диаметра при допустимом напоре ΔH.
Задают диаметр дюкера в первом приближении. Находят коэффициент скорости:
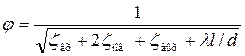 . (7.4.2)
. (7.4.2)
Коэффициенты потерь: на вход 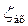 = 0,5, на поворот
= 0,5, на поворот  = 0,05 при угле поворота ≈ 20° и
= 0,05 при угле поворота ≈ 20° и  = 1,1 при угле поворота ≈ 90°, на выход
= 1,1 при угле поворота ≈ 90°, на выход 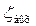 = 1. Гидравлический коэффициент трения железобетонных труб λ = 0,019.
= 1. Гидравлический коэффициент трения железобетонных труб λ = 0,019.
Скорость воды в дюкере
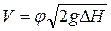 , (7.4.3)
, (7.4.3)
диаметр
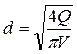 . (7.4.4)
. (7.4.4)
Полученное значение диаметра берётся в качестве второго приближения и т. д.
Диаметр дюкера округляют до стандартного и тогда пересчитывают разность уровней на входе и выходе
 . (7.4.5)
. (7.4.5)
§
Требуется спроектировать дождевую водоотводящую сеть участка городской территории, план которого представлен на рис. 7.5.11. Длина стороны клетки равна 25 м. На плане показаны шесть кварталов, разделённых улицами и река, в которую предполагается сбрасывать сточные воды дождевой водоотводящей сети. На план нанесены горизонтали – линии равной высоты над уровнем моря: 96 м, 97 м, 98 м, 99 м.
Расчёт производится в соответствии с рекомендациями СНиП 2.04.03-85. «Канализация. Наружные сети и сооружения».
Намечаем трассу рассчитываемого водостока (синие линии). Уличный коллектор – труба, собирающая воду с дождеприёмников. Уличные коллекторы проектируются прямолинейными, параллельно красным линиям застройки и располагаются, по возможности по середине проезжей части.
Намеченную трассу разбиваем на расчётные участки и наносим на ней дождеприёмники. Под расчётным участком сети подразумевают отрезок его в пределах кварталов (между поперечными улицами). На плане видим магистральные участки 1-2, 2-3, 3-4, 4-5. К узлам 2, 3 и 4 подходят расчётные участки с боковых улиц.
Дождеприёмники, изображённые на плане в виде маленьких прямоугольников, надлежит предусматривать в лотках проезжей части улиц, а также в пониженных местах и до пешеходных переходов. Расстояние l между дождеприёмниками зависит от уклона земли i [5]. При i < 0,004 l = 50 м, при i < 0,004…0,006 l = 60 м, при i < 0,006…0,01 l = 70 м.
Уклон земли боковых участков iземли < 0,004. Уклон земли участков 1-2 и 2-3 iземли = 0,005. В соответствии с рекомендациями для всех этих участков принимаем расстояние между дождеприёмниками lcon = 50 м.
Уклон земли участка 3-4 iземли = 0,008. В соответствии с рекомендациями для этого участка принимаем расстояние между дождеприёмниками lcon = 200/3 = 66,7 м.
Первый дождеприёмник и первая точка сети от вышележащей границы квартала устраивается на расстоянии, равном расстоянию между дождеприёмниками.
Разбиваем кварталы на площади стока, тяготеющие к каждому участку сети. Границы площадей стока показаны красными отрезками. Для определения площади стока проводят биссектрисы углов (между осями улиц) до их взаимного пересечения и соединяют прямой линией образующиеся вершины треугольников.
Уклон местности на плане рис. 7.5.11 не превышает 0,01. Если уклон местности превышает 0,02, разбивка территории на бассейны, как это видно на рис. 7.5.12, значительно усложняется.
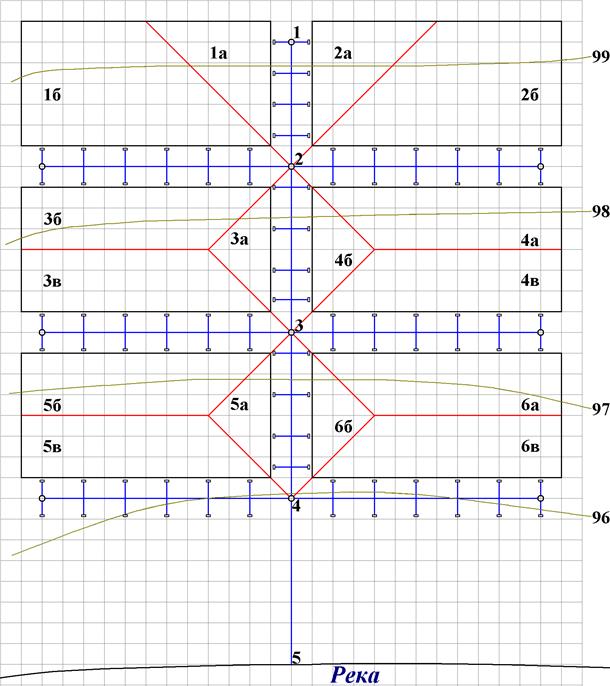
Рис. 7.5.11. Разбиение участка городской территории на площади стока.
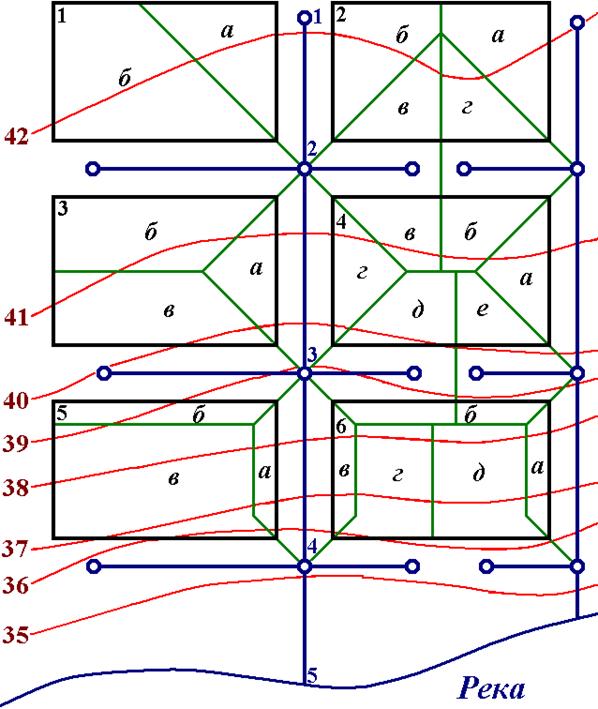
Рис. 7.5.12. Разбиение участка городской территории со сложным рельефом на площади стока.
На рис. 7.5.13а показана площадь, прилегающая к участку 1-2, на рис. 7.5.13б – площадь, примыкающая к участку 2-3 и площади боковых подключений к этому участку, на рис. 7.5.13в – площадь, примыкающая к участку 3-4 и площади боковых подключений к этому участку, на рис. 7.5.13г – площадь боковых подключений к участку 4-5. В табл. 7.5.1 приведены результаты расчёта площадей стока.


а б

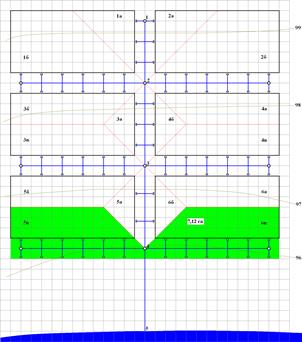
в г
Рис. 7.5.12. Площади стока, прилегающие к участкам сети ливневой канализации.
Таблица 7.5.1. Площади стока.
| № участка | Прилегающая к участку площадь стока | Площадь стока боковых подключений | Общая площадь стока, га | ||
| обозначение | га | обозначение | га | ||
| 1-2 | 1а, 2а | 3,06 | – | 3,06 | |
| 2-3 | 3а, 4б | 2,00 | 1б, 3б, 2б, 4а | 13,82 | 3,06 2 13,82 = 18,88 |
| 3-4 | 5а, 6б | 2,00 | 3в, 5б, 4в, 6а | 11,00 | 18,88 2 11 = 31,88 |
| 4-5 | – | 5б, 6в | 7,12 | 31,88 7,12 = 39,00 |
По карте рис. 7.5.7 (СНиП 2.04.03-85, черт. 1) для Донецка интенсивность дождя продолжительностью 20 мин с вероятным периодом превышения один раз в год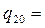 88 л/с/га.
88 л/с/га.
Из табл. 7.5.2 (СНиП 2.04.03-85, табл. 5) при средних условиях расположения коллекторов на проездах местного значения и 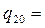 88 л/с/га период однократного превышения расчётной интенсивности дождя P = 0,5…1 год. Принимаем P = 1 год.
88 л/с/га период однократного превышения расчётной интенсивности дождя P = 0,5…1 год. Принимаем P = 1 год.
Таблица 7.5.2. Период однократного превышения расчётной интенсивности дождя.
Из табл. 7.5.3 (СНиП 2.04.03-85, табл. 4) для востока Украины при P = 1 год показатель степени n = 0,67, среднее количество дождей за год mr = 60, показатель степени γ = 1,82.
Параметр расчётной продолжительности дождя (СНиП 2.04.03-85, п. 2.12)
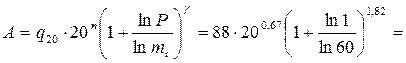 655 л/с/га =
655 л/с/га =
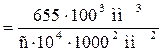 = 0,0655 мм/с = 3,93 мм/мин.
= 0,0655 мм/с = 3,93 мм/мин.
По табл. 7.5.3 (СНиП 2.04.03-85, табл. 10) при А = 655 л/с/га среднее значение коэффициента стока для водонепроницаемых поверхностей (кровли зданий и асфальтобетонное покрытие дорог) zmid = 0,27.
Таблица 7.5.3. Коэффициент, характеризующий поверхность бассейна стока.
| Параметр A | Коэффициент z для водонепроницаемых поверхностей |
| 0,28 0,27 |
Время поверхностной концентрации дождевого стока в населённых пунктах (по грунту, по крышам, по дорожному покрытию) при отсутствии внутриквартальных закрытых дождевых сетей (СНиП 2.04.03-85, п. 2.16) принимается равным 5…10 мин. Примем tcon = 5 мин.
Начальные дождеприёмники участков устанавливаем на расстоянии 25 м от границ кварталов. Тогда длина бокового участка lcan = 325 – 25 = 300 м.
Продолжительность протекания дождевых вод по уличным лоткам до дождеприёмника tcan рассчитывается только при отсутствии дождеприёмников в пределах квартала (СНиП 2.04.03-85, п. 2.15).
С учётом СНиП 2.04.03-85, п. 2.34, расчётную скорость течения по лоткам и трубам, обеспечивающую незаиливание канализационных сетей, примем равной vcan = vр = 1,0 м/с.
Для участка 1-2 и для боковых участков время протекания к началу участка складывается из времени поверхностной концентрации и времени протекания по уличному лотку к первому дождеприёмнику (СНиП 2.04.03-85, п. 2.15 и 2.16):
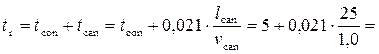 5,5 мин.
5,5 мин.
Расчётная продолжительность протекания дождевых вод по поверхности и трубам боковых участков (СНиП 2.04.03-85, п. 2.15 и 2.16)
 10,6 мин.
10,6 мин.
Расчётная продолжительность протекания дождевых вод по поверхности и трубам участка 1-2 (СНиП 2.04.03-85, п. 2.15 и 2.16)
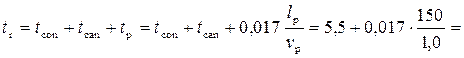 8,1 мин.
8,1 мин.
Расход дождевых вод (в л/с)
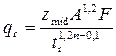 .
.
Согласно табл. 7.5.4 (СНиП 2.04.03-85, табл. 11) при n = 0,67 коэффициент, учитывающий заполнение свободной ёмкости сети в момент возникновения напорного режима, β = 0,665.
Таблица 7.5.4. Коэффициент β в формуле расчётного расхода дождевых вод.
| Показатель степени n | ≤ 0,4 | 0,5 | 0,6 | ≥ 0,7 |
| Значение коэффициента β | 0,8 | 0,75 | 0,7 | 0,65 |
Расчётный расход дождевых вод для гидравлического расчёта дождевых сетей (СНиП 2.04.03-85, п. 2.11) 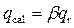 , л/с.
, л/с.
Согласно СНиП 2.04.03-85 (п. 4.30) принимаем ширину потока в лотке перед решёткой (ширину разлива) b = 2 м.
На рис. 7.5.14 показаны типы открытых дождевых сетей: а – борт-лоток бетонный треугольный, б – то же армированный прямоугольный, в – то же армированный трапецеидальный, г – кювет мощённый или одернованный. Выбираем борт-лоток бетонный треугольный как более дешёвый, более удобный в эксплуатации.
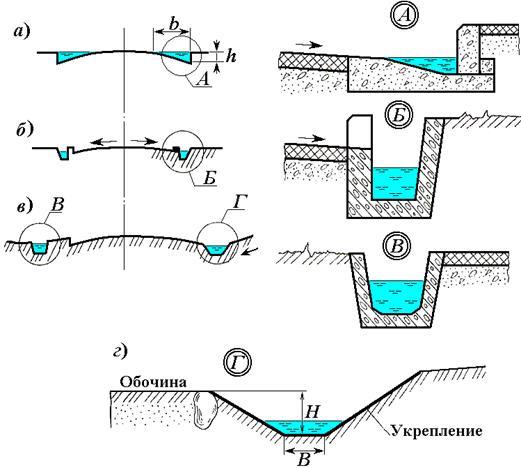
Рис. 7.5.14. Типы открытых дождевых сетей: а – борт-лоток бетонный треугольный, б – то же армированный прямоугольный, в – то же армированный трапецеидальный, г – кювет мощённый или одернованный.
Согласно СНиП 2.04.03-85 (п. 2.42) наименьший уклон лотков проезжей части imin = 0,003. Поскольку уклон земли вдоль лотка на боковых участках меньше этой величины, применяем лоток с пилообразным продольным профилем, продольный разрез которого показан на рис. 7.5.15. Здесь 1 – поверхность дорожного покрытия; 2 – дно лотка; 3 – дождеприёмник; 4 – металлическая решетка; 5 – перепускная труба к коллектору.
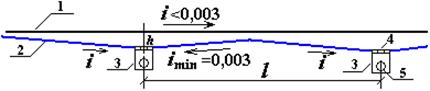
Рис. 7.5.15. Продольный разрез лотка с пилообразным продольным профилем.
Площадь стока до дождеприёмника, установленного в начале участка 1, (ширина квартала 150 м плюс половина ширины улицы 25 м, помноженные на расстояние 25 м от границы квартала до первого дождеприёмника) F = (1,50 0,25)·0,25 = 0,44 га.
Расход дождевых вод через лоток до первого дождеприёмника участка 1
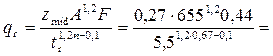 85,7 л/с.
85,7 л/с.
При минимальном уклоне лотка i = 0,003 и глубине лотка у дождеприёмника h = il = 0,003·25 = 0,075 м отметка дождеприёмника будет ниже отметки земли на величину, равную глубине лотка у дождеприёмника h = il = 0,003·25 = 0,075 м.
Площадь сечения потока в лотке ω = hb/2 = 0,075·2/2 = 0,075 м². Смоченный периметр χ ≈ b h = 2 0,075 = 2,08 м. Гидравлический радиус R = ω/χ = 0,075/2,08 ≈ 0,036 м.
Для бетонированных лотков коэффициент шероховатости  0,014.
0,014.
Показатель степени в формуле скоростной характеристики
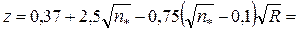
 .
.
Скоростная характеристика 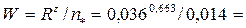 7,88 м/с.
7,88 м/с.
Расходная характеристика K = ωW = 0,075∙7,88 = 0,591 м3/с.
Скорость 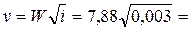 0,43 м/с.
0,43 м/с.
Расход 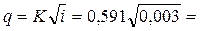 0,032 м3/с = 32 л/с, что меньше расчётного значения
0,032 м3/с = 32 л/с, что меньше расчётного значения 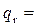 85,7 л/с. Поэтому увеличиваем уклон лотка до i = 0,006.
85,7 л/с. Поэтому увеличиваем уклон лотка до i = 0,006.
Тогда глубина лотка у дождеприёмника h = il = 0,006·25 = 0,15 м. Площадь сечения потока в лотке ω = hb/2 = 0,15·2/2 = 0,15 м².
Смоченный периметр χ ≈ b h = 2 0,15 = 2,15 м.
Гидравлический радиус R = ω/χ = 0,15/2,15 ≈ 0,070 м.
Скоростная характеристика 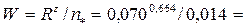 12,3 м/с.
12,3 м/с.
Расходная характеристика K = ωW = 0,15∙12,3 = 1,84 м3/с.
Расход 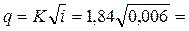 0,142 м3/с = 142 л/с, что больше рассчитанного значения
0,142 м3/с = 142 л/с, что больше рассчитанного значения 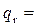 85,7 л/с.
85,7 л/с.
Скорость 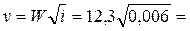 0,95 м/с.
0,95 м/с.
Минимальную допустимую скорость дождевых сточных вод в лотках следует принимать (СНиП 2.04.03-85, п. 2.35) 0,4 м/с, максимальную (п. 2.36) – 7 м/с. Оба эти требования выполняются.
На участках лотков 1-2, 2-3 и 3-4 необходимый расход и скорость потока обеспечиваются за счёт уклона земли i ≥ 0,005 и меньшей площади водосбора, приходящейся на дождеприёмник.

Рис. 7.5.16. Борт-лоток бетонный треугольный.
Согласно СНиП 2.04.03-85 (п. 4.29) дождеприёмники с горизонтальным отверстием в пониженных местах лотков с пилообразным продольным профилем и на участках с продольным уклоном менее 0,005 оборудуются малой прямоугольной дождеприёмной решёткой (рис. 7.5.17а). На участках улиц с продольным уклоном 0,005 или более и в пониженных местах в конце затяжных участков спусков дождеприёмники с горизонтальным отверстием должны быть оборудованы большой прямоугольной решёткой (рис. 7.5.17б).
На рис. 7.5.18 показан чертёж дождеприёмника из сборных железобетонных элементов.
Согласно СНиП 2.04.03-85 (п. 2.33) наименьший диаметр труб самотёчных уличных дождевых сетей следует принимать 250 мм.
Расчётные наполнения и минимальные уклоны в зависимости от диаметра труб [10, с. 154] приведены в табл. 7.5.5.
Таблица 7.5.5. Расчётные наполнения и минимальные уклоны труб.
| Диаметр d, мм | ||||||
| Наполнение, h/d | 0,75 | 0,75 | 0,8 | 0,8 | 0,8 | 0,8 |
| Минимальный уклон | 0,0016 | 0,0012 | 0,0010 | 0,00083 | 0,00071 | 0,00065 |
Железобетонные трубы, применяемые при устройстве подземных безнапорных трубопроводов, транспортирующих самотёком бытовые жидкости и атмосферные сточные воды, изготовляют по ГОСТ 6582–71 [5, с 125, табл. 24]. Их размеры приведены в табл. 7.5.6.
Таблица 7.5.6. Толщина стенки трубы.
| Диаметр условного прохода d, мм | ||||||||||
| Толщина tc, мм |
Согласно СНиП 2.04.03-85 (п. 4.7) соединение трубопроводов разных диаметров следует предусматривать в колодцах по шелыгам (вершинам внутреннего свода) труб. На рис. 7.5.19а показано соединение канализационных труб в колодцах по уровням воды, а на рис. 7.5.19б – шелыга в шелыгу.
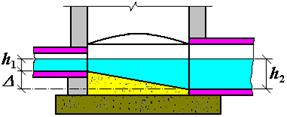
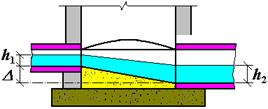
а б
Рис. 7.5.19. Соединение канализационных труб в колодцах: а – по уровням воды, б – шелыга в шелыгу.
Для трубопроводов дождевой и общесплавной систем водоотведения следует принимать полное расчётное наполнение (СНиП 2.04.03-85, п. 2.40). Наименьшие скорости при наибольшем расчётном наполнении приведены в табл. 7.5.7 (СНиП 2.04.03-85, табл. 16).
Таблица 7.5.7. Наименьшие незаиливающие скорости.
| Диаметр d, мм | Скорость vmin, м/с, при наполнении h/D | |||
| ≤ 0,6 | ≤ 0,7 | ≤ 0,75 | ≤ 0,8 | |
| 150–250 | 0,7 | – | – | – |
| 300–400 | – | 0,8 | ||
| 450–500 | – | – | 0,9 | – |
| 600–800 | – | – | – | |
| – | – | 1,15 | – | |
| 1000–1200 | – | – | – | 1,15 |
| – | – | – | 1,3 | |
| > 1500 | – | – | – | 1,5 |
Для боковых участков, примыкающих к узлу 2, расчётный расход сточных вод
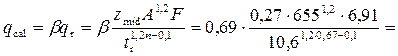 585 л/с,
585 л/с,
уклон земли i = 0. Выбираем d = 1000 мм. При наполнении 0,60d и уклоне i = 0,0015 [10, с. 76, табл. 18] обеспечивается необходимая незаиливающая скорость v = 1,19 > 1,15 м/с (табл. 7.5.7) и расход q = 583,3 ≈ 585 л/с. Падение трубы il = 0,0015·300 = 0,45 м.
Уточняем расчётную продолжительность протекания дождевых вод по поверхности и трубам боковых участков, примыкающих к узлу 2:
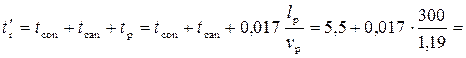 9,8 мин.
9,8 мин.
Уточняем расход по трубам боковых участков, примыкающих к узлу 2:
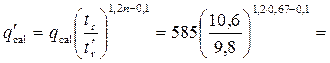 619 л/с.
619 л/с.
По таблицам Лукиных [10, с. 76] для такого расхода получаем практически ту же скорость v = 1,20 м/с. Следовательно, уточнённое время протекания по боковым участкам, примыкающим к узлу 2, равно 9,8 мин.
Результаты этих и дальнейших расчётов заносим в табл. 7.5.8.
С учётом времени протекания 8,1 мин от наиболее удалённых площадей для участка 1-2 расчётный расход сточных вод
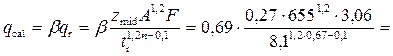 313 л/с,
313 л/с,
уклон земли участка 1-2 iземли = 1/190 ≈ 0,005. Для соединения с трубой бокового участка, примыкающего к узлу 2, падение участка 1-2 должно составить 99,16 – 98,33 0,45 = 1,28 м. Уклон трубы ip = 1,28/150 = 0,0085.
По таблицам Лукиных [10, с. 61] получаем, что труба диаметром d = 600 мм при наполнении 0,55d и уклоне i = 0,0085 обеспечивает требуемый расход при скорости v = 1,95 м/с, превышающей минимальную незаиливающую скорость (табл. 7.5.7), равную 1 м/с. Принимаем диаметр трубы участка 1-2 d = 600 мм.
Уточняем расчётную продолжительность протекания дождевых вод по поверхности и трубам участка 1-2:
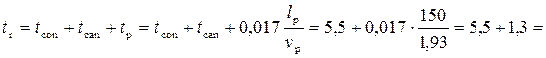 6,8 мин.
6,8 мин.
Уточняем расход по трубам участка 1-2:
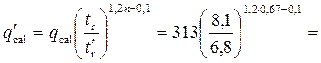 354 л/с.
354 л/с.
По таблицам Лукиных [10, с. 61] для такого расхода получаем практически ту же скорость v = 2,01 м/с. Следовательно, уточнённое время протекания по участку 1-2 равно 6,8 мин.
Расчётную продолжительность протекания дождевых вод по трубам участка 2-3 находим, принимая скорость равной скорости на предыдущем участке 1-2 (СНиП, п. 2.15, 2.16):
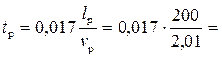 1,7 мин.
1,7 мин.
С учётом времени протекания 9,8 мин от наиболее удалённых площадей боковых участков, примыкающих к узлу 2, время протекания по участку 2-3 составит tr = 9,8 1,7 = 11,5 мин.
Расход на участке 2-3
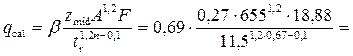 1510 л/с,
1510 л/с,
уклон земли iземли = 1/190 ≈ 0,005. Примем такой же уклон трубы ip = 0,005. По таблицам Лукиных [10, с. 78] получаем, что труба диаметром d = 1000 мм при наполнении 0,80d и уклоне i = 0,005 обеспечивает расход q = 1550 л/с при скорости v = 2,30 м/с, превышающей минимальную незаиливающую скорость (табл. 7.5.7), равную 1,15 м/с. Принимаем диаметр трубы участка 2-3 d = 1000 мм.
Уточняем расчётную продолжительность протекания дождевых вод по трубам участка 2-3:
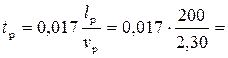 1,4 мин.
1,4 мин.
С учётом времени протекания 9,8 мин от наиболее удалённых площадей боковых участков 1 и 2 время протекания по участку 2-3 составит tr = 9,8 1,4 = 11,2 мин.
Уточняем расход на участке 2-3
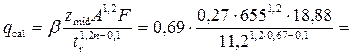 1538 л/с.
1538 л/с.
По таблицам Лукиных [10, с. 78] для такого расхода получаем практически ту же скорость v = 2,30 м/с. Следовательно, уточнённое время протекания по участку 2-3 равно 1,4 мин.
С учётом времени протекания 10,6 мин от наиболее удалённых площадей для боковых участков, примыкающих к узлу 3, расчётный расход сточных вод
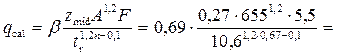 466 л/с,
466 л/с,
уклон земли i = 0. Падение трубы 97,5 – 97,4 0,45 = 0,55. Уклон трубы ip = 0,55/300 = 0,0018. Выбираем d = 800 мм. При наполнении 0,75d и уклоне i = 0,0018 [10, с. 68) обеспечивается необходимая незаиливающая скорость v = 1,19 > 1 м/с (табл. 7.5.7) и расход q = 479,7 > 466 л/с.
Уточняем расчётную продолжительность протекания дождевых вод по поверхности и трубам боковых участков, примыкающих к узлу 3:
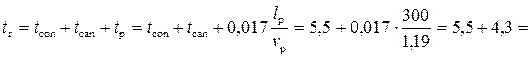 9,8 мин.
9,8 мин.
Уточняем расход по трубам боковых участков, примыкающих к узлу 3:
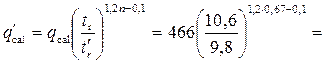 492 л/с.
492 л/с.
По таблицам Лукиных [10, с. 68] для такого расхода получаем ту же скорость v = 1,19 м/с. Следовательно, уточнённое время протекания по участкам, примыкающим к узлу 3, равно 9,8 мин.
Расчётную продолжительность протекания дождевых вод по трубам участка 3-4 находим (СНиП, пп. 2.15, 2.16), принимая скорость равной скорости на предыдущем участке 2-3:
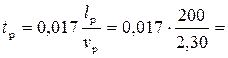 1,5 мин.
1,5 мин.
С учётом времени протекания 9,8 мин от наиболее удалённых площадей боковых участков, примыкающих к узлу 2, а также времени протекания 1,4 мин по трубам участка 2-3 время протекания по участку 3-4 составит tr = 9,8 1,4 1,5 = 12,7 мин.
Расход на участке 3-4
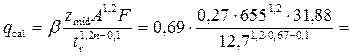 2378 л/с,
2378 л/с,
уклон земли iземли = 1/125 = 0,008. Примем такой же уклон трубы ip = 0,008. По таблицам Лукиных [10, с. 86] получаем, что труба диаметром d = 1200 мм при наполнении 0,8d и уклоне i = 0,008 обеспечивает расход q = 3195 л/с при скорости v = 3,29м/с, превышающей минимальную незаиливающую скорость (табл. 7.5.7), равную 1,15 м/с. Принимаем диаметр трубы участка 3-4 d = 1200 мм.
Уточняем расчётную продолжительность протекания дождевых вод по трубам участка 3-4:
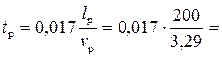 1,0 мин.
1,0 мин.
С учётом времени протекания 9,8 мин от наиболее удалённых площадей боковых участков, примыкающих к узлу 2, и трубам участка 2-3 1,4 мин время протекания по участку 3-4 составит tr = 9,8 1,4 1,0 = 12,2 мин.
Уточняем расход на участке 3-4
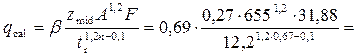 2446 л/с.
2446 л/с.
По таблицам Лукиных [10, с. 86] для такого расхода получаем практически ту же скорость v = 2,9 м/с. Следовательно, уточнённое время протекания по трубам участка 3-4 равно 1,0 мин.
Для боковых участков, примыкающих к узлу 4, расчётный расход сточных вод
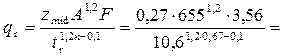 302 л/с,
302 л/с,
уклон земли i ≈ 0,001. Падение трубы 96,3 – 95,9 0,45 = 0,85.
Уклон трубы ip = 0,85/300 ≈ 0,003. Выбираем d = 800 мм. При наполнении 0,50d и уклоне i = 0,003 [10, с. 69] обеспечивается необходимая незаиливающая скорость v = 1,35 > 1,0 м/с (табл. 7.5.7) и расход q = 340 > 302 л/с.
Уточняем расчётную продолжительность протекания дождевых вод по поверхности и трубам боковых участков, примыкающих к узлу 4:
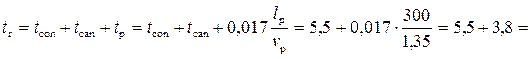 9,3 мин.
9,3 мин.
Уточняем расход по трубам боковых участков, примыкающих к узлу 4:
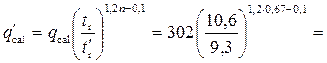 331 л/с.
331 л/с.
По таблицам Лукиных [10, с. 69] для такого расхода получаем практически ту же скорость v = 1,32 м/с. Следовательно, уточнённое время протекания по боковым участкам, примыкающим к узлу 4, равно 9,3 мин.
Расчётную продолжительность протекания дождевых вод по трубам участка 4-5 находим (СНиП 2.04.03-85, пп. 2.15, 2.16), принимая скорость равной скорости на предыдущем участке 3-4:
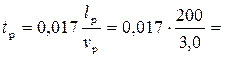 1,1 мин.
1,1 мин.
С учётом времени протекания 12,2 мин от наиболее удалённых площадей боковых участков, примыкающих к узлу 2, время протекания по участку 4-5 составит tr = 12,2 1,1 = 13,3 мин.
Расход на участке 4-5
 2816 л/с.
2816 л/с.
Уклон земли равен (95,96 – 95,00)/200 = 0,0048. Для получения минимальной глубины залегания коллектора падение трубы должно составлять 95,96 – 95,00 – 0,45 = 0,51 м (разность отметок земли минус дополнительное падение 0,45 м в точке 2 для обеспечения необходимого уклона на боковых участках). Уклон трубы ip = 0,51/200 ≈ 0,0025. По таблицам Лукиных [10, сс. 101, 105) получаем, что необходимый расход обеспечивает труба диаметром d = 1600 мм при наполнении 0,65d, уклоне i = 0,0025 и скорости v = 2,1 м/с, превышающей минимальную незаиливающую скорость (табл. 7.5.7), равную 1,5 м/с. Принимаем диаметр трубы участка 4-5 d = 1600 мм. Уточняем расчётную продолжительность протекания дождевых вод по трубам участка 4-5:
 1,6 мин.
1,6 мин.
С учётом времени протекания 12,2 мин от наиболее удалённых площадей боковых участков 1 и 2 время протекания по участку 4-5 составит tr = 12,2 1,6 = 13,8 мин.
Уточняем расход на участке 4-5
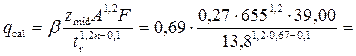 2743 л/с.
2743 л/с.
По таблицам Лукиных [10, (сс. 101, 105] для такого расхода получаем практически ту же скорость v = 2,1 м/с. Следовательно, уточнённое время протекания по участку 4-5 равно 1,6 мин.
Наименьшую глубину заложения канализационных трубопроводов необходимо принимать на основании опыта эксплуатации сетей в данном районе. Изолинии распределения глубин (в см) промерзания грунтов показаны на карте рис. 7.5.20.
Рис. 7.5.20. Изолинии глубин промерзания грунтов (см).
Таблица 7.5.8. Результаты расчётов трубопровода.
| Участок | 1-2 | бок 2 | 2-3 | бок 3 | 3-4 | бок 4 | 4-5 | |
| Длина участка l, м | ||||||||
| Площадь стока F, га | 3,06 | 6,91 | 18,88 | 5,5 | 31,9 | 3,56 | 39,0 | |
| Время протекания, мин | К началу участка | 5,5 | 5,5 | 9,8 | 5,5 | 11,2 | 5,5 | 12,2 |
| По участку | 1,3 | 4,3 | 1,4 | 4,3 | 1,0 | 3,8 | 1,6 | |
| Всего | 6,8 | 9,8 | 11,2 | 9,8 | 12,2 | 9,3 | 13,8 | |
| Расчётный расход qcal, л/с | ||||||||
| Диаметр d, м | 0,60 | 1,00 | 1,00 | 0,80 | 1,20 | 0,80 | 1,60 | |
| Скорость v, м/с | 1,95 | 1,20 | 2,30 | 1,19 | 2,90 | 1,32 | 2,10 | |
| Уклон земли iземли, ‰ | 5,0 | 0,0 | 5,0 | 0,0 | 8,0 | 1,0 | 4,8 | |
| Уклон трубопровода iр, ‰ | 8,5 | 1,5 | 5,0 | 1,8 | 8,0 | 3,0 | 2,5 | |
| Падение, м | 1,28 | 0,45 | 1,06 | 0,55 | 1,60 | 0,85 | 0,51 |
При отсутствии данных по эксплуатации минимальную глубину заложения лотка трубопровода допускается принимать (СНиП 2.04.03-85, п. 4.8): для труб диаметром до 500 мм – на 0,3 м; для труб большего диаметра – на 0,5 м менее большей глубины проникновения в грунт нулевой температуры, не менее 0,7 м до верха трубы, считая от отметок поверхности трубы или планировки. Трубопроводы, укладываемые на глубину 0,7 м и менее, считая от верха трубы, должны быть предохранены от промерзания и повреждения наземным транспортом. Принимаем наименьшую глубину заложения шелыги (верхнего свода) трубы h = 0,7 м.
На рис. 7.5.21 показано рациональное размещение подземных коммуникаций. Здесь Э – электросети, Т – телефонный кабель, Г – газопровод, В – водопровод, К – канализация, КТ – кабели троллейбуса, Д – дождеприёмники, ВС – водосток.
Тип основания под трубы необходимо принимать в зависимости от несущей способности грунтов и нагрузок (СНиП 2.04.03-85, п. 4.10).
Во всех грунтах, за исключением скальных, плавунных, болотистых и просадочных I типа, необходимо предусматривать укладку труб непосредственно на выровненное и утрамбованное дно траншеи.
В скальных грунтах необходимо предусматривать укладку труб на подушку толщиной не менее 10 см из местного песчаного или гравелистого грунта, в илистых торфянистых и других слабых грунтах – на искусственное основание.
На рис. 7.5.22 показан поперечный профиль уличного лотка. Здесь В – ширина проезжей части, b – ширина разлива, h – глубина слоя воды в уличном лотке, i – поперечный уклон проезжей части, Н – глубина заложения уличного коллектора дождевой сети.
Рис. 7.5.21. Рациональное размещение подземных коммуникаций.
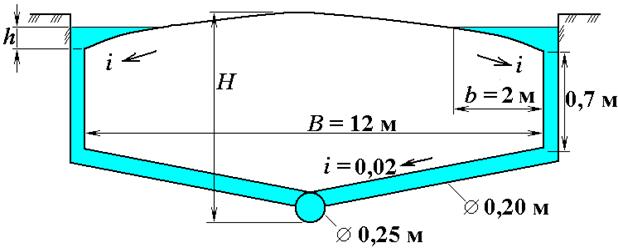
Рис. 7.5.22. Поперечный профиль уличного лотка.
Глубина заложения дождевого коллектора в узле 1
H = h il D tc = 0,7 0,02·6 0,60 0,06 = 1,48 м,
где h = 0,7 м – глубина заложения шелыги трубопровода у первого дождеприёмника, i = 0,02 – уклон трубопровода от дождеприёмника до уличного коллектора, l = B/2 = 6 м – расстояние от дождеприёмника до уличного коллектора, принимаемое равным половине ширины проезжей части улицы, D = 0,60 м – диаметр уличного коллектора, tc = 0,06 м – толщина стенки трубы уличного коллектора (табл. 7.5.6).
Падение трубы на участке 1-2 Δz = 1,28 м подсчитано ранее. Падение трубы на участке 2-3 равно разности отметок земли в начале и в конце участка Δz = 98,33 – 97,27 = 1,06 м; на участке 3-4 Δz = 97,27 – 95,96 = 1,31 м. Падение трубы на участке 4-5 Δz = 0,51 м подсчитано ранее.
Отметка земли в начале участка 1-2 zз = 99,16 м, отметка дна трубы в начале участка 1-2 zдн = zз – H = 99,16 – 1,48 = 97,68 м. Отметку шелыги свода начала участка 1-2 находим, прибавляя диаметр трубы к отметке дна: zш = zд d = 97,68 0,60 = 98,28 м. Отметку шелыги трубы в конце участка найдём, вычтя из отметки шелыги в её начале падение:
zшк = zшн – Δz = 98,28 – 1,28 = 97,00 м.
Отметка шелыги конца участка является отметкой дна начала следующего участка.
Глубина заложения дна трубы равна разности отметок земли и дна.
На рис. 7.5.23 показан незатопленный выпуск поверхностных вод в водоток с откосом, укреплённым железобетонной плитой, где УВВ – уровень высокой воды, УМВ – уровень малой воды.
Рис. 7.5.23. Незатопленный выпуск поверхностных вод в водоток с откосом, укреплённым железобетонной плитой.
Таблица 7.5.9. Результаты расчёта продольного профиля коллектора.
| Участок | 1-2 | 2-3 | 3-4 | 4-5 | |
| Длина трубы, м | |||||
| Уклон земли, ‰ | 5,0 | 5,0 | 8,0 | 4,8 | |
| Уклон трубы, ‰ | 8,5 | 5,0 | 8,0 | 2,5 | |
| Диаметр трубы, м | 0,60 | 1,00 | 1,20 | 1,60 | |
| Наполнение трубы | 0,55d | 0,80d | 0,70d | 0,65d | |
| Падение, м | 1,28 | 1,06 | 1,31 | 0,51 | |
| Отметка земли, м | Начало | 99,16 | 98,33 | 97,27 | 95,96 |
| Конец | 98,33 | 97,27 | 95,96 | 95,00 | |
| Отметка дна трубы, м | Начало | 97,68 | 96,00 | 94,74 | 93,03 |
| Конец | 96,40 | 94,94 | 93,43 | 92,52 | |
| Отметка шелыги свода, м | Начало | 98,28 | 97,00 | 95,94 | 94,63 |
| Конец | 97,00 | 95,94 | 94,63 | 94,12 | |
| Глубина заложения дна трубы, м | Начало | 1,48 | 2,33 | 2,53 | 2,93 |
| Конец | 1,93 | 2,33 | 2,53 | 2,48 |
На рис. 7.5.24 показан продольный профиль коллектора, а в табл. 7.5.10 сведены данные для построения этого профиля.
Таблица 7.5.10. Сводка данных для построения профиля коллектора.
| Номер колодца | |||||
| Отметка земли | 99,16 | 98,33 | 97,27 | 95,96 | 95,00 |
| Отметка шелыги | 98,28 | 97,00 | 95,94 | 94,63 | 94,12 |
| Отметка дна конца участка | – | 96,40 | 94,94 | 93,43 | 92,52 |
| Отметка дна начала участка | 97,68 | 96,00 | 94,74 | 93,03 | – |
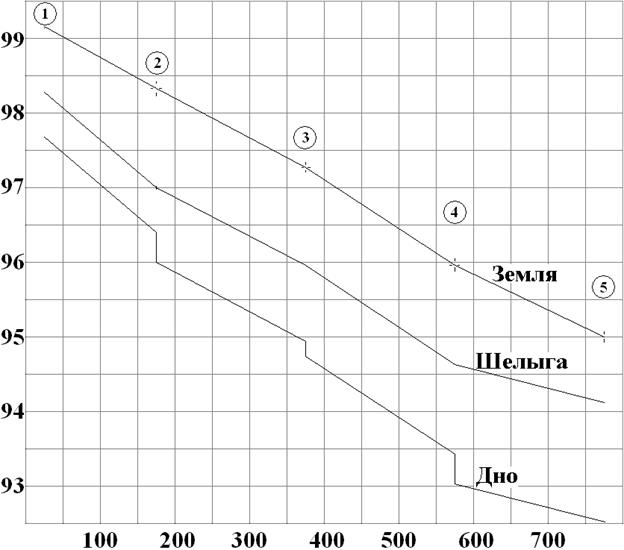
Рис. 7.5.24. Продольный профиль коллектора.
ВАЖНЕЙШИЕ ФОРМУЛЫ
ТМЖГ
• Манометрическое (или избыточное) давление (Па) – это превышение абсолютного давления над атмосферным:
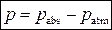 .
.
Нормальное атмосферное давление patm = 1,013·105 Па.
• Вакуумметрическое давление (или вакуум) – это разность между атмосферным давлением и абсолютным давлением в точке, когда абсолютное давление меньше атмосферного:
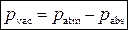 .
.
• Уравнение Эйлера представляет собой основной закон динамики применительно к жидкости: сумма силы давления, действующей единицу массы жидкости, и ускорения массовых сил (сил инерции и тяжести) равна ускорению единицу массы жидкости:
 .
.
где ρ – плотность жидкости, p – давление, X – проекция ускорения массовой силы на ось x, ux – проекция скорости на ось x.
• Основное дифференциальное уравнение гидростатики следует из уравнений Эйлера:
dp = ρ(Xdx Ydy Zdz).
• Уравнение поверхности уровня (равного давления):
Xdx Ydy Zdz = 0.
Его физический смысл: элементарная работа массовых сил по перемещению единицы массы жидкости по поверхности уровня равна нулю.
• Основное уравнение гидростатики: давление в некоторой точке покоящейся жидкости равняется сумме давления p0, приложенного к свободной поверхности жидкости, и давления столба жидкости γh над этой точкой:
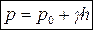 ,
,
где h – глубина (м), на которой находится точка, γ = ρg = 1000·9,81 = 9810 Н/м3 – удельный вес (вес единицы объёма).
• Гидравлический радиус сечения (м) – отношение площади живого сечения (м2) к смоченному периметру (м):
R = ω/χ.
Для напорного течения в трубе диаметром D гидравлический радиус R = D/4.
• Уравнение неразрывности потока: если между двумя сечениями нет притока и оттока воды, то расход (м3/с) для этих сечений одинаков:
Q1 = Q2 или V1ω1 = V2ω2,
где V – средняя скорость по сечению.
• Число Рейнольдса для круглой трубы диаметром D
Re = VD/ν,
где ν – кинематическая вязкость; для воды при t = 20°C ν = 10-6 м2/с. Для русел некруглого сечения и безнапорных труб, как и в других формулах вместо D подставляем эквивалентный диаметр Deq = 4R.
• Уравнение Бернулли: полный напор в сечении выше по течению равняется полному напору в сечении ниже по течению плюс потери напора h:
 .
.
Напор (м) – это удельная (на единицу веса) энергия: геометрический напор z – потенциальная энергия положения, напор давления p/γ – потенциальная энергия давления, скоростной напор αV2/(2g) – кинетическая энергия. Корректив кинетической энергии (коэффициент Кориолиса) α учитывает неравномерность распределения скоростей по сечению. Для турбулентного движения α = 1,1.
• Пьезометрический уклон – это уклон пьезометрической линии (линии удельной потенциальной энергии), соединяющей отметки пьезометров:
Удельная энергия сечения потока
Вспомним, что удельной энергией потока называется сумма
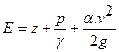 .
.
Удельной энергией сечения потока по определению называется сумма
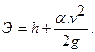
Удельная энергия потока вследствие потерь на трение убывает вниз по течению потока. Удельная энергия сечения потока при равномерном движении остается для всех сечений постоянной, так как при равномерном движении и скорость течения и глубина постоянны по длине потока. Т.о. если удельная энергия потока определяется относительно произвольно выбранной, но одной и той же для разных сечений, плоскости сравнения, удельная энергия сечения потока определяется относительно своей для каждого сечения плоскости сравнения, проходящей через нижнюю точку живого сечения (рис. 2 – 1 и 2 – 2).
Заменяя среднюю скорость течения v отношением расхода Q к площади поперечного сечения w и принимая a @ 1, получим следующее выражение для удельной энергии сечения потока:
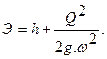
Критическая глубина – это глубина, при которой удельная энергия сечения потока при данном расходе принимает минимальное значение.
Состояние потока при критической глубине называется критическим. Критическими называются и все гидравлические элементы потока, соответствующие его критическому состоянию. Они обозначаются с индексом “к“ – vк, ωк, Rк, Cк и т.д.
Критическая глубина потока может быть найдена как экстремум непрерывной функции Э = Э (h). Для этого приравняем нулю первую производную функции:
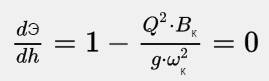
Критическая глубина зависит только от расхода и не зависит от уклона русла
Нормальная глубинаh0– устанавливающаяся при заданном расходе и при равномерном движении
Уравнение Шези для равномерного движения
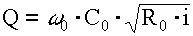
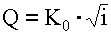
Критический уклон
Существует такой уклон при котором hк = h0
В уравнение Шези подставим параметры при этом условии и найдем Q.
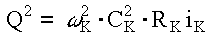
В уравнение 11 подставим значение Q
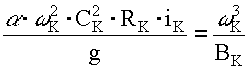
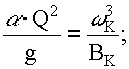
Получим:
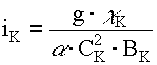
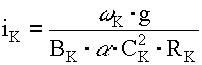
или
так как R = w / c
§
Действительную глубину потока обозначим h.
1. h > h,спокойное состояние потока (при равномерном или неравномерном движении)
2. h < h –бурное состояние потока
3. 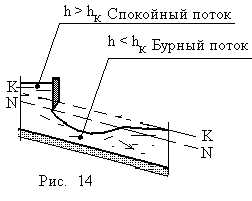 h = h– критическое состояние потока, всегда равномерное движение.
h = h– критическое состояние потока, всегда равномерное движение.
Исследование форм свободной поверхности потока при i > 0.

Интегрирование дифференциального уравнения неравномерного движения воды в случае, когда i > 0 по способу Бахметьева.
Б.А. Бахметьев предложил для интегрирования уравнения (3.23) в случае i > 0 использовать показательную зависимость
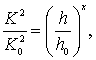 (3.24)
(3.24)
где x – называется гидравлическим показателем русла;
h – действительная глубина в рассматриваемом поперечном сечении;
h0 – нормальная глубина, определяемая по формуле Шези;
К, К0 – модули расхода, отвечающие этим глубинам.
Логарифмируя (3.24), получим
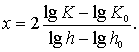 (3.25)
(3.25)
Модуль расхода определен точно для некоторых типов русел: весьма узкие прямоугольные, х = 2,0; широкие прямоугольные, х = 3,4; узкие параболические, х = 3,7; широкие параболические, х = 4,4; треугольные, х = 5,4.
Для трапецеидального русла
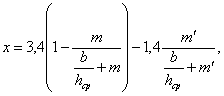 (3.26)
(3.26)
где b – ширина русла по дну;
m – коэффициент откоса; 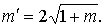
Рассмотрим интегрирование уравнения (3.23) по методу Б.А.Бахметьева
1. Уклон дна i > О
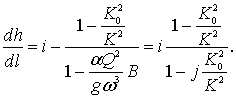 (3.27)
(3.27)
Введем дополнительное обозначение
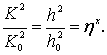 (3.28)
(3.28)
где h/h0 – относительная глубина, откуда h = ηh0 или
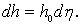
Учитывая принятое обозначение (3.28), уравнение (3.27) запишется
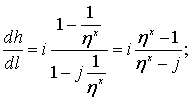 (3.29)
(3.29)
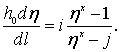
Разделяя переменные, получим
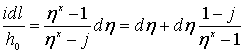 (3.30)
(3.30)
или
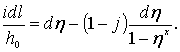
Прежде чем проинтегрировать уравнение (3.30), рассмотрим продольный разрез потока (рисунок 3.14) и выделим часть потока сечениями 1–1 и 2–2. Обозначим:
l – длина кривой свободной поверхности между сечениями;
h1, h2 – глубина потока в верхнем и нижнем сечениях потока;
h0 – нормальная глубина.
Дифференциальное уравнение было составлено для произвольной элементарной части потока длиной dl. Интегрируя уравнение (3.30) от сечения 1–1 до сечения 2–2, получим
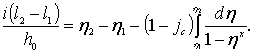 (3.31)
(3.31)
Считая, что для данного русла х = const; подынтегральную функцию в уравнении (3.31) следует рассматривать как функцию только η. Поэтому можно записать
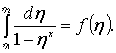 (3.32)
(3.32)
Окончательно уравнение кривой свободной поверхности запишется
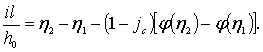 (3.33)
(3.33)
В этом уравнении
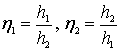 – относительные глубины в соответствующих сечениях;
– относительные глубины в соответствующих сечениях;
j1, j2 – коэффициент изменения кинетической энергии;
jc0,5(j1 j2) – вычисляются по зависимости соответствен но для глубин h1 и h2.
Величины 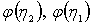 были вычислены путем разложения подынтегральной функции (3.32) в ряд для различных значений η и x. Результаты вычислений сведены в таблицу [6], [16].
были вычислены путем разложения подынтегральной функции (3.32) в ряд для различных значений η и x. Результаты вычислений сведены в таблицу [6], [16].
Пользуясь уравнением (3.33), можно решить следующие задачи:
1) известна глубина h1 (или h2), требуется определить глубину h2 (или h1) в сечении потока, расположенном на заданном расстоянии l от сечения с глубиной h1 (или h2);
2) известны h1 и h2, требуется определить расстояние l между сечениями с заданными глубинами;
3) известны глубины h1 и h2, требуется построить кривую свободной поверхности АВ.
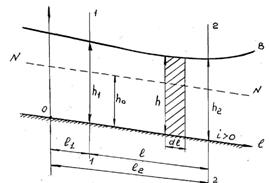
§
§
При устройстве водобойной стенки дно нижнего бьефа не опускается, поэтому величины сжатой глубины и, следовательно, глубины сопряженной сжатой не изменяются. Если водобойная стенка работает как неподтопленный водослив практического профиля, то задача решается без подбора.
Расчет выполняется следующим образом.
1. Из формулы водослива
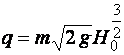 , (5.11)
, (5.11)
где m – коэффициент расхода водослива, получаем зависимость для полного напора водослива
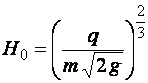 . (5.12)
. (5.12)
2. Вычисляется значение геометрического напора водослива
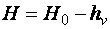 , (5.13)
, (5.13)
где hv – скоростной напор;
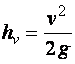 . (5.14)
. (5.14)
3. Определяется высота водобойной стенки
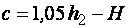 . (5.15)
. (5.15)
4. Если водослив не подтоплен, то проверяют сопряжение бьефов ниже водобойной стенки. При наличии отогнанного прыжка проектируют следующую водобойную стенку меньшей высоты.
5. Если водослив подтоплен, то задачу приходится решать подбором. Задаются рядом высот водобойной стенки. Для этих высот вычисляются: геометрические и полные напоры на водосливе; высоты подтопления; степени подтопления 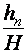 .
.
6. Используя степень подтопления, интерполяцией данных табл. 5.3 определяют коэффициент подтопления.
ª
Водослив с тонкой стенкой
Прямоугольный водослив
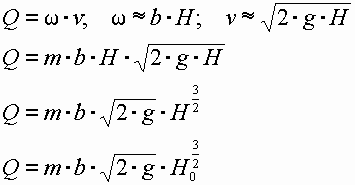
Нормальный водослив 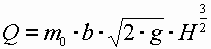
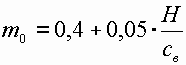
Подтопленный водослив с тонкой стенкой
- горизонт воды нижнего бьефа располагается выше гребня водослива
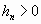
- в нижнем бьефе спокойный режим движения
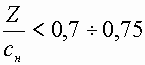
Базен 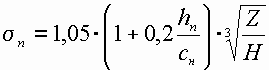
Треугольный водослив с тонкой стенкой 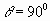
Томсон 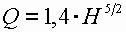
Прибоковом сжатии при входе на водослив с широким порогом линии тока ( з плане) искривляются. В связи с боковым сжатием происходят дополнительные потери энергии, особенно на участке расширения потока за сжатым сечением. Коэффициент скорости ф и коэффициент расхода т водослива при боковом сжатии уменьшаются по сравнению с истечением через водослива без бокового сжатия. Отметим, что боковое сжатие происходит и в случае, если ширина по дну подводящего русла ( канала) равна ширине водослива с широким порогом, а площадь живого сечения в подводящем канале больше, чем площадь живого сечения на пороге водослива. Для этого достаточно, чтобы при равенстве указанных ширин площадь живого сечения в подводящем русле была больше площади живого сечения во входном сечении водослива.
§
§
Водослив практического профиля. Основная расчетная формула (коэффициенты m, σ, ε).
3.1. Общие сведения Водосливы, отличные от водосливов с тонкой стенкой и с широким порогом, называются водосливами практического профиля. Толщина их стенки обычно лежит в пределах δ=(0.5…2 )Н. Водосливы практического профиля могут быть с поли- гональным (прямоугольным, трапецеидальным) и криволи- нейным (безвакуумные, вакуумные), очертаниями. Водосливы полигонального очертания применяются как водопропускные сооружения при малых расходах воды и как гасители энергии. Водосливы криволинейного очертания служат водосливными плотинами в гидроузлах. Безвакуумные водосливы (рис. 3.1) имеют вертикальную (верховую) напорную грань, а сливная (низовая) грань очер- чена по форме нижней поверхности струи, переливающейся через неподтопленный водослив с тонкой стенкой. Очертание такого водослива строится по опытным данным Кригера – Офицерова и обеспечивает его плавное обтекание и атмо- сферное давление под струёй. Коэффициент расхода такого водослива m=0.48…0.51, что существенно больше, чем для водослива с тонкой стенкой. Если сливная поверхность срезана (на рис. 3.1 показана пунктиром), то под струёй устанавливается давление менее атмосферного, а водослив называется вакуумным и коэффи- циент расхода увеличивается до m=0.54…0.57. 15 Условия подтопления водосливов практического профи- ля те же, что и для водосливов с тонкой стенкой. Рис. 3.1. Водослив практического профиля
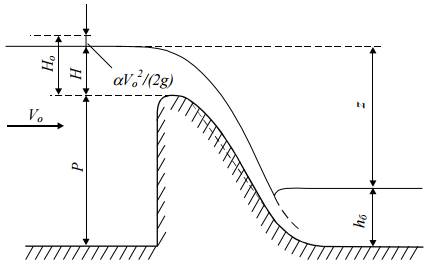
§
Гидравлический расчет водобойного колодца состоит в определении глубины колодца и его длины.
Определение глубины колодца. Затопление прыжка в водобойном колодце осуществляется путем увеличения глубины в нижнем бьефе за счет опускания дна колодца 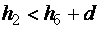 . Но одновременно с опусканием дна колодца растет высота падения струи с порога перепада, что приводит к уменьшению сжатой глубины и, как следствие, росту глубины сопряженной сжатой. Таким образом, вторая сопряженная глубина зависит от глубины колодца, поэтому данную задачу приходится решать подбором или графически.
. Но одновременно с опусканием дна колодца растет высота падения струи с порога перепада, что приводит к уменьшению сжатой глубины и, как следствие, росту глубины сопряженной сжатой. Таким образом, вторая сопряженная глубина зависит от глубины колодца, поэтому данную задачу приходится решать подбором или графически.
Порядок расчета следующий:
1) задаемся произвольной величиной глубины колодца d0;
2) находим значение полного напора 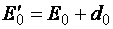 ;
;
3) по найденному значению полного напора определяем величину сжатой глубины, решая (5.6);
4) вычисляем вторую сопряженную глубину, используя основное уравнение прыжка:
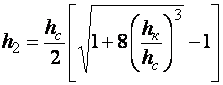 ; (5.7)
; (5.7)
5) сравниваем найденную величину h2 с 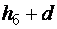 , если данные величины не равны, задаемся новым значением глубины колодца и повторяем пп. 1–5;
, если данные величины не равны, задаемся новым значением глубины колодца и повторяем пп. 1–5;
6) для ускорения решения задачи вычисления по пп. 1–5 заносятся в таблицу (см. пример 7);
7) по двум последним графам табл. 5.2 строятся графики 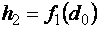 и
и  (см. пример 7);
(см. пример 7);
8) точка пересечения графиков даст теоретическую глубину колодца d0;
9) для затопления прыжка найденную глубину колодца необходимо увеличить на 5¸10 %.
Определение длины колодца. Длина водобойного колодца равна сумме длины отлета струи и величины, несколько меньшей длины гидравлического прыжка
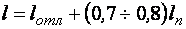 . (5.8)
. (5.8)
В этом случае в колодце установится так называемый подпертый прыжок.
Длина отлета струи находится по уравнению
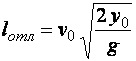 . (5.9)
. (5.9)
Длина прыжка может быть найдена, например, по формуле Павловского
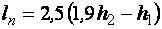 . (5.10)
. (5.10)
§
В водосливных плотинах, водосбросных сооружениях, быстротоках водный поток сбрасывается из верхнего бьефа в нижний обычно с большими скоростями и кинетич. энергией, во много раз превышающий энергию речного потока в бытовых условиях, вследствие чего в нижнем бьефе сооружения могут возникать глубокие размывы дна реки или канала с опасными подмывами сооружения. Для предупреждения подмыва сооружения из-за наличия избыточной энергии русло водотока в нижнем бьефе плотины надлежащим образом закрепляют и принимают меры к погашению избыточной энергии потока воды, переливающейся в нижний бьеф.
Многие способы гашения энергии потока основываются на использовании явления прыжка гидравлического, при к-ром часть избыточной кинетич. энергии с увеличением глубины потока преобразуется в потенциальную, но значит, часть «теряется», переходя в тепловую. Если глубина воды в нижнем бьефб в пределах закрепленной части дна недостаточна для возникновения прыжка, то для его образования применяются спец. устройства — гасители энергии.
К наиболее простым гасителям относится водобойный колодец— углубление во флютбете со стороны нижнего бьефа. Глубина колодца должна создавать такие условия, чтобы в его пределах возникал гидравлич. прыжок, т. е. чтобы струя, сходящая с сооружения, затапливалась. Устраиваются также гасители энергии потока в виде отдельных выступов различной формы, располагаемых в нижнем бьефе за водосливной частью сооружения (шашки, пирсы и т. п.), или непрерывных поперечных конструкций (водобойные стенки, зубчатые пороги и пр.). Гашение энергии потока достигается и устройством в конце водосливной грани носка, отклоняющего переливающуюся через сооружение струю от дна, т. е. создающего т. н. поверхностный режим потока в нижнем бьефе. Поверхностный режим облегчает сброс через плотину плавающих тел (льда, бревен).
При водобойной стенке в нижнем бьефе образуется бассейн, гидравлич. эффективность к-рого для гашения энергии потока подобна водобойному колодцу. В других случаях устройством гасителей снижение скоростей течения достигается вследствие усиленного завихрения потока и разделения его на отдельные, по-разному направленные струи. К таким конструкциям относятся шашечные гасители, отклоняющие струи воды в стороны и вверх, зубчатые пороги, расщепляющие струи по глубине и отчасти по ширине, и балочные гасители, расщепляющие струи по глубине.
§
Гидравлический расчет водобойного колодца состоит в определении глубины колодца и его длины.
Определение глубины колодца. Затопление прыжка в водобойном колодце осуществляется путем увеличения глубины в нижнем бьефе за счет опускания дна колодца 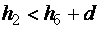 . Но одновременно с опусканием дна колодца растет высота падения струи с порога перепада, что приводит к уменьшению сжатой глубины и, как следствие, росту глубины сопряженной сжатой. Таким образом, вторая сопряженная глубина зависит от глубины колодца, поэтому данную задачу приходится решать подбором или графически.
. Но одновременно с опусканием дна колодца растет высота падения струи с порога перепада, что приводит к уменьшению сжатой глубины и, как следствие, росту глубины сопряженной сжатой. Таким образом, вторая сопряженная глубина зависит от глубины колодца, поэтому данную задачу приходится решать подбором или графически.
Порядок расчета следующий:
1) задаемся произвольной величиной глубины колодца d0;
2) находим значение полного напора 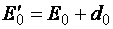 ;
;
3) по найденному значению полного напора определяем величину сжатой глубины, решая (5.6);
4) вычисляем вторую сопряженную глубину, используя основное уравнение прыжка:
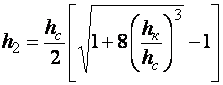 ; (5.7)
; (5.7)
5) сравниваем найденную величину h2 с 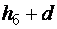 , если данные величины не равны, задаемся новым значением глубины колодца и повторяем пп. 1–5;
, если данные величины не равны, задаемся новым значением глубины колодца и повторяем пп. 1–5;
6) для ускорения решения задачи вычисления по пп. 1–5 заносятся в таблицу (см. пример 7);
7) по двум последним графам табл. 5.2 строятся графики 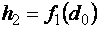 и
и  (см. пример 7);
(см. пример 7);
8) точка пересечения графиков даст теоретическую глубину колодца d0;
9) для затопления прыжка найденную глубину колодца необходимо увеличить на 5¸10 %.
§
Расчет начинается с определения, требуется или нет гаситель энергии воды у перепада. На рис. 11 показана схема перепада с основными гидравлическими параметрами.

Рис. 11. Расчетная схема одноступенчатого перепада
Гаситель энергии у перепада можно не применять, если 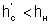 , т. е. в нижнем бьефе имеет место затопленный прыжок.
, т. е. в нижнем бьефе имеет место затопленный прыжок.
Гаситель энергии необходим, если 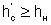 , т. е. имеет место отогнанный или надвинутый прыжок.
, т. е. имеет место отогнанный или надвинутый прыжок.
Здесь 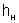 – нормальная (бытовая) глубина воды до и после перепада при установившемся режиме потока и при установленных – расходе воды
– нормальная (бытовая) глубина воды до и после перепада при установившемся режиме потока и при установленных – расходе воды 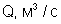 ; ширине лотка перепада
; ширине лотка перепада 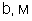 ; уклоне дна водотока перед перепадом
; уклоне дна водотока перед перепадом 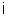 и коэффициенте шероховатости бетонного лотка
и коэффициенте шероховатости бетонного лотка 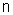 (
(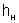 определяется подбором по формулам (1) – (7), с построением графика зависимости:
определяется подбором по формулам (1) – (7), с построением графика зависимости: 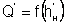 при прямоугольном русле);
при прямоугольном русле);
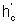 – сопряженная глубина с
– сопряженная глубина с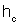 определяемая по формуле:
определяемая по формуле:
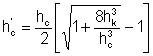 , (8)
, (8)
где 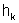 – критическая глубина (глубина воды на уступе), определяемая по формуле
– критическая глубина (глубина воды на уступе), определяемая по формуле
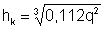 , (9)
, (9)
где 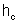 – глубина воды в сжатом сечении, определяемая по уравнению
– глубина воды в сжатом сечении, определяемая по уравнению
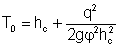 , (10)
, (10)
где 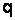 – удельный (на единицу ширины водослива) расход воды, определяемый по заданному расходу воды
– удельный (на единицу ширины водослива) расход воды, определяемый по заданному расходу воды 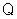 и ширине
и ширине 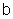 лотка водослива:
лотка водослива:
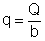 , (11)
, (11)
где 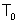 – полный напор воды на уступе с учетом скоростного напора, определяемый по формуле
– полный напор воды на уступе с учетом скоростного напора, определяемый по формуле
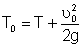 , (12)
, (12)
где 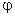 – коэффициент скорости, принимаемый в пределах 0,85–1,00;
– коэффициент скорости, принимаемый в пределах 0,85–1,00; 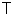 – напор воды на уступе, определяемый по формуле
– напор воды на уступе, определяемый по формуле
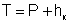 , (13)
, (13)
где 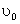 – скорость воды на уступе, определяемая по формуле
– скорость воды на уступе, определяемая по формуле
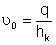 , (14)
, (14)
где 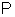 – высота стенки перепада;
– высота стенки перепада; 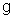 – ускорение силы тяжести, 9,81 м/с2.
– ускорение силы тяжести, 9,81 м/с2.
Для нахождения 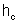 из уравнения (10) задаются несколькими значениями
из уравнения (10) задаются несколькими значениями 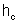 , затем для каждого из них находят
, затем для каждого из них находят 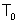 по (10). Затем строится график зависимости:
по (10). Затем строится график зависимости: 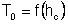 . По этому графику, зная
. По этому графику, зная 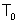 из выражения (12), определяют
из выражения (12), определяют 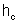 .
.
Определив по формуле (8) 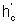 , решают, требуется или нет гаситель энергии воды у перепада. Если требуется, тогда рассчитывается гаситель энергии. В районах с суровым климатом следует применять гаситель энергии с водобойной стенкой.
, решают, требуется или нет гаситель энергии воды у перепада. Если требуется, тогда рассчитывается гаситель энергии. В районах с суровым климатом следует применять гаситель энергии с водобойной стенкой.
В пределах гасителя энергии развивается большая скорость потока воды, поэтому, чтобы выбрать укрепление (см. прил. 4) водобойной части перепада, определяется скорость течения воды в сжатом сечении по формуле Ю.Н. Даденкова:
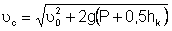 , (15)
, (15)
где 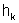 и
и 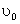 – см. формулы (9) и (13).
– см. формулы (9) и (13).
§
§
§
§








