Магнитный поток единица измерения буква

Квантование магнитного потока

При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:

Φ0=he{displaystyle Phi _{0}={frac {h}{e}}},

где h{displaystyle h} — постоянная Планка, e{displaystyle e} — элементарный заряд.

Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов.

Φs=Φ02=h2e=2,067833758×10−15{displaystyle Phi _{s}={frac {Phi _{0}}{2}}={frac {h}{2e}}=2{,}067833758times 10^{-15}} Вб (в СИ);

Φs=hc2e=2,067833636×10−7{displaystyle Phi _{s}={frac {hc}{2e}}=2,067833636times 10^{-7}} Гаусс·см² (в СГС), c{displaystyle c} — скорость света.

Экспериментально квантование магнитного потока было обнаружено в 1961 году.

Магнитный поток

Вектор магнитной индукции →B характеризует магнитное поле в каждой точке пространства.

Можно ввести еще одну величину, зависящую от значения вектора →B не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром.

Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль →n к плоскости проводника составляет угол α с направлением вектора магнитной индукции →B (см. рисунок).

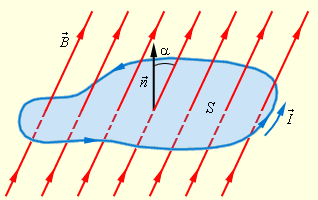
Произведение Bcos.α=Bn представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:

Φ=BnS

Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.

Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Выразим модуль вектора магнитной индукции:

В=ΦScos.α..

Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:

0,20,5cos.(90°−30°)..=0,20,5·0,5..=0,8 (Тл)

Некоторые свойства магнитного потока

В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции B{displaystyle mathbf {B} } через любую замкнутую поверхность S{displaystyle S} равен нулю:

Φ=∮SB⋅dS=0{displaystyle Phi =oint limits _{S}mathbf {B} cdot {text{d}}mathbf {S} =0}.

Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.

В соответствии с теоремой Стокса, магнитный поток Φ{displaystyle Phi } через поверхность, «натянутую» на некий контур L{displaystyle L}, можно выразить через циркуляциювекторного потенциала A{displaystyle mathbf {A} } магнитного поля по этому контуру:

Φ=∮LA⋅dl{displaystyle Phi =oint limits _{L}mathbf {A} cdot mathbf {dl} },

Определение магнитного потока

Магнитным потоком через бесконечно малый элемент поверхности dS{displaystyle {rm {d}}S} называется произведение

dΦ=BdScos⁡α=B⋅dS{displaystyle dPhi =B,{rm {d}}S,cos alpha =mathbf {B} cdot {rm {d}}mathbf {S} },

где α{displaystyle alpha } — угол между вектором магнитной индукции B{displaystyle mathbf {B} } и единичным вектором нормалиn{displaystyle mathbf {n} } к участку поверхности, а векторный элемент dS площади поверхности S определяется как

dS=dSn{displaystyle {rm {d}}mathbf {S} ={rm {d}}S,mathbf {n} }.

Магнитным потоком через поверхность конечной площади называется интеграл от dΦ{displaystyle dPhi } по поверхности:

Φ=∫dΦ=∬SB⋅dS{displaystyle Phi =int {rm {d}}Phi =iint limits _{S}mathbf {B} cdot {rm {d}}mathbf {S} }.

Направление вектора n{displaystyle mathbf {n} } в общем случае непостоянно (см. рис.), магнитное поле также может изменяться вдоль поверхности. Точка в произведениях означает скалярное умножение векторов. Интеграл понимается как предел суммы по малым участкам при стремлении их размеров к нулю. Поверхность может быть незамкнутой (как на рис.) или замкнутой.
В случае однородного поля и плоской поверхности магнитный поток рассчитывается как Φ=BScos⁡α{displaystyle Phi =B,S,cos alpha }.