Напряженность и электрическое смещение электростатического поля.
Напряженность электростатического поля – это силовая характеристика электростатического поля, численно равная силе, действующей на единичный положительный заряд.
Напряженность электростатического поля – векторная величина: E = F/Qпробный
Единица напряженности – вольт на метр (В/м)
Электростатическое поле представляется графически силовыми линиями или линиями напряженности .
Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации(Смещение электрических зарядов вещества под действием электрического поля)
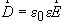Единицей электрического смещения является кулон на метр квадратный (Кл/м2).
, где e0 – электрическая постоянная; e – относительная диэлектрическая проницаемость среды;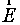 
– вектор напряженности электрического поля.
Направление вектора электрического смещения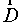 
совпадает с направлением вектора напряженности 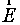. Согласно определению вектора электрического смещения 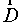и выражения можно записать
.
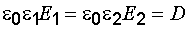Напряженность поля точечного заряда.
Напряженность электростатического поля (точечного заряда):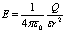 
где r – расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность
Примеры формул напряженности поля заряженных тел.
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
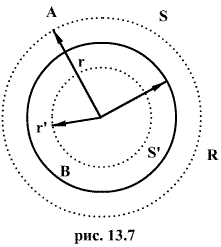Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 
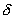заряда в любой точке сферы будет одинакова.
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
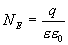
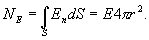
По теореме Гаусса
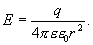
Следовательно
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
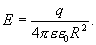Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е.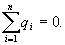 
Следовательно, по теореме Гаусса, 
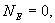и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю.
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью . 
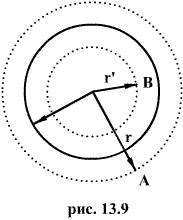
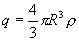В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда ,расположенного в центре шара.
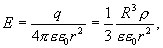
Тогда вне шара
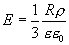
а на его поверхности (r=R)
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом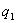 
, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
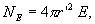
с другой стороны, в соответствии с теоремой Гаусса
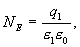
Из сопоставления последних выражений следует
где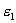 
– диэлектрическая проницаемость внутри шара.
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью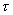 
.
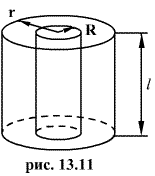
Проведем коаксиальную цилиндрическую поверхность радиуса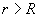 
Поток вектора напряженности через эту поверхность
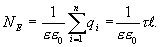
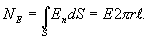
По теореме Гаусса
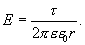Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
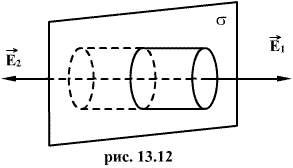
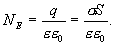Суммарный поток вектора; напряженности равен вектору 
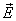, умноженному на площадь S первого основания, плюс поток вектора 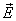через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают.
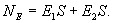Таким образом, с другой стороны по теореме Гаусса
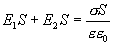
Следовательно
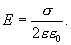но 
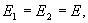тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
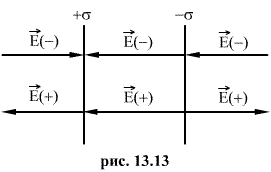Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов 
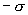и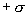 
, равны сумме напряженностей полей, создаваемых пластинами, т.е.
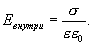
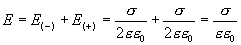
Таким образом,
Вне пластины векторы 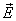от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
2.3.
§
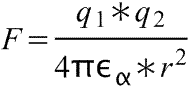где
F – сила взаимодействия двух точечных зарядов
q1, q2– величины зарядов
εα – абсолютная диэлектрическая проницаемость среды
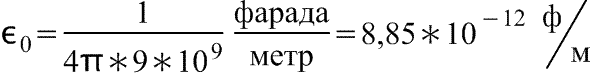r – расстояние между точечными зарядами
Консервативность электростатического взаимодействия.
Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2.
Работа на пути dl равна:
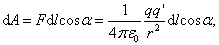
где dr – приращение радиус-вектора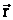 
при перемещении на dl; 
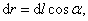т. е.
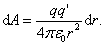
Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу:
Работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально.
Потенциал электростатического поля.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: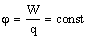
– энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Потенциал электростатического поля точечного заряда.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
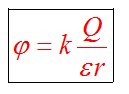
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Формула работы электростатического поля.
На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.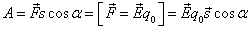 
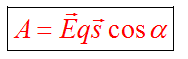
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Связь напряженности электростатического поля с потенциалом.
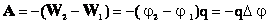
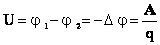
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.
Электроемкость проводника и конденсатора.
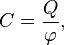Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд
Формула электроемкости плоского конденсатора.
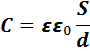
Энергия электрического поля.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.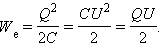 
2.5.
Электрический ток.
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц
Условия возникновения и существования электрического тока.
1. наличие свободных носителей зарядов,
2. наличие разности потенциалов. это условия возникновения тока,
3. замкнутая цепь,
4. источник сторонних сил, который поддерживает разность потенциалов.
Сторонние силы.
Сторонние силы – силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.
Э.д.с. Напряжение.
Электродвижущая сила (ЭДС)— физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил
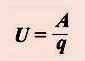Напряжение ( U )равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.
Единица измерения напряжения в системе СИ:
[ U ] = 1 B
Сила тока.
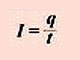Сила тока ( I )-скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
Плотность тока.
Плотность тока j— вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.
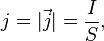
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).
§
Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь 
. Правда в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле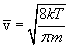 
. Для комнатной температуры ( 
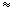300К) вычисление по этой формуле приводит к следующему значению: 
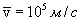. При включении поля на хаотическое тепловое движение, происходящее, со скоростью 
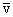, накладывается упорядоченное движение электронов с некоторой средней скоростью 
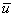. Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью :
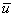Предельная допустимая техническими нормами плотность тока для медных проводов составляет около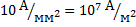 
Таким образом, даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в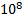 
раз меньше средней скорости теплового движения .
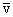Работа электрического тока.
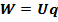
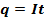
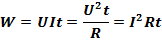
Закон Джоуля-Ленца.
При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.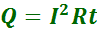 
2.8.
Магнитное взаимодействие.
Магнитное взаимодействие — это взаимодействие упорядочение движущихся электрических зарядов.
Магнитное поле.
Магнитное поле – это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
Сила Лоренца и сила Ампера.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью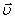 
положительный заряд (здесь 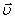– скорость упорядоченного движения носителей положительного заряда). Модуль лоренцевой силы: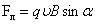 
Сила Ампера– это сила, с которой магнитное поле действует на проводник с током.
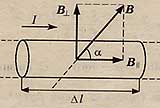
Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индукции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки.
Индукция и напряженность магнитного поля.
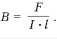Магнитная индукция –векторная физическая величина, характеризующая магнитное поле. Вектор магнитной индукции всегда направлен по касательной к магнитной линии
Расчетная формула:
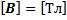
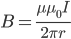Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током
B – магнитная индукция
μ – относительная магнитная проницаемость
μ0 – магнитная постоянная
I – сила тока
r – расстояние до проводника
Магнитная индукция поля в центре кругового тока (витка)
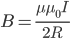
B – магнитная индукция
μ – относительная магнитная проницаемость
μ0 – магнитная постоянная
I – сила тока
R – радиус
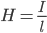Напряженностью магнитного поляназывают векторную величину 
, характеризующую магнитное поле и определяемую следующим образом: , 
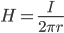Напряжённость магнитного поля: бесконечной прямой провод
H – напряжённость магнитного поля
I – сила тока
r – расстояние до проводника
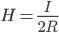Напряжённость магнитного поля в центре витка
H – напряжённость магнитного поля
I – сила тока
R – радиус
Закон Био-Савара-Лапласа.
Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
Формулировка
Пусть постоянный ток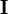 
течёт по контуру γ, находящемуся в вакууме, 
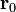—точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
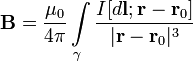
Направление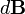 
перпендикулярно 
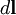и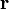 
, то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление 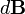, еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора 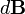определяется выражением (в системе СИ)
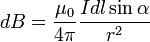
Векторный потенциал даётся интегралом (в системе СИ)
2.9.
§
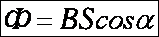Магнитный поток (поток линий магнитной индукции)через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром.
Формула работы силы Ампера при движении прямого проводника с постоянным током в однородном магнитном поле.
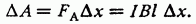
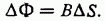
Таким образом, работа силы Ампера может быть выражена через силу тока в перемещаемом проводнике и изменение магнитного потока через контур, в который включен этот проводник: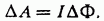 
Индуктивность контура.
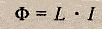Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
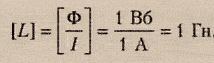где Ф – магнитный поток через контур, I – сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Энергия магнитного поля.
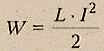Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
2.10.
Электромагнитная индукция.
Электромагнитная индукция— явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Опыты Фарадея. Объяснение электромагнитной индукции.
Если подносить постоянный магнит к катушке или наоборот (рис.3.1), то в катушке возникнет электрический ток. То же самое происходит с двумя близко расположенными катушками: если к одной из катушек подключить источник переменного тока, то в другой также возникнет переменный ток , но лучше всего этот эффект проявляется, если две катушки соединить сердечником
По определению Фарадея общим для этих опытов является следующее: если поток вектора индукции, пронизывающий замкнутый, проводящий контур, меняется, то в контуре возникает электрический ток.
Это явление называют явлением электромагнитной индукции, а ток – индукционным. При этом явление совершенно не зависит от способа изменения потока вектора магнитной индукции.
Формула э.д.с. электромагнитной индукции.
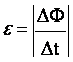ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Правило Ленца.
Правило Ленца
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван.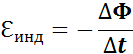
2.11.
Самоиндукция, ее объяснение.
Самоиндукция – явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
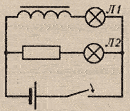Замыкание цепи
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи ( вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
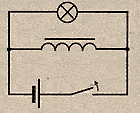Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток ( стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).
Формула э.д.с. самоиндукции.
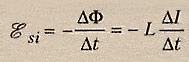ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
2.12.
Первое и второе положения теории электромагнитного поля Максвелла.
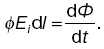1. Всякое перемещенное электрическое поле порождает вихревое магнитное поле. Переменное электрическое поле было названо Максвеллом, так как оно, подобно обычному току, вызывает магнитное поле. Вихревое магнитное поле порождается как токами проводимости Iпр (движущимися электрическими зарядами), так и токами смещения (перемещенным электрическим полем Е).
Первое уравнение Максвелла
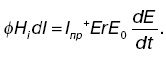2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).
Второе уравнение Максвелла:
Электромагнитное излучение.
Электромагни́тные во́лны, электромагни́тное излуче́ние— распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.
3.1. Волна– это колебания, распространяющиеся в пространстве в течение времени.
Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле. Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.
Продольные волны возникают тогда, когда частицы среды колеблются, ориентируясь вдоль вектора распространения возмущения. Поперечные волны распространяются в перпендикулярном вектору воздействия направлении. Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
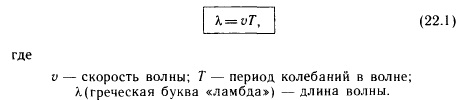
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду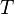 
колебаний, поэтому
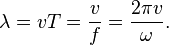
Волновое число (такженазываемое пространственной частотой) — это отношение 2π радиан к длине волны: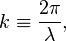 
пространственный аналог круговой частоты.
Определение: волновым числом k называется быстрота роста фазы волны φ по пространственной координате.
3.2. Плоская волна — волна, фронт которой имеет форму плоскости.
Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как фронт плоской волны начинается в 
и заканчивается в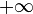 
, чего, очевидно, быть не может.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции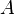 
записывается в ви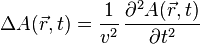де:
где
· 
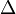– оператор Лапласа;
· 
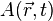— искомая функция;
· 
— радиус вектора искомой точки;
· 
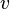— скорость волны;
· 
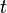— время.
Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Частный случай волновой поверхности — волновой фронт.
А) Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей. 
Б) Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер.
Луч — линия, нормальной и волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская — параллельные прямые).
Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях, смысл понятия луч теряется.
3.3. Энергетические характеристики волны
Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m0 находится по формуле: Е0 = m0 Α2ω2/2. В единице объема среды содержится n = p/m0 частиц (ρ– плотность среды). Поэтому единица объема среды обладает энергией wр = nЕ0 = ρΑ2ω2/2.
Объемная плотность энергии (Wр)- энергия колебательного движения частиц среды, содержащихся в единице ее объема: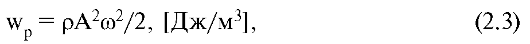 
Поток энергии (Ф) – величина, равная энергии, переносимой волной через данную поверхность за единицу времени: 
Интенсивность волны или плотность потока энергии (I) – величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны: 
3.4. Электромагнитная волна
Электромагнитная волна – процесс распространения электромагнитного поля в пространстве.
Условие возникновения электромагнитных волн. Изменения магнитного поля происходят при изменении силы тока в проводнике, а сила тока в проводнике изменяется при изменении скорости движения электрических зарядов в нем, т. е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только электрическое поле. При постоянной скорости заряда возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.
Электромагнитные волны распространяются в веществе с конечной скоростью.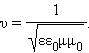 
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
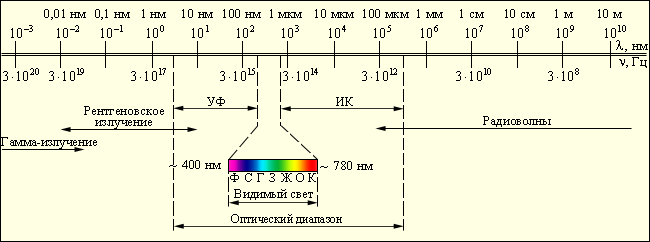
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше.
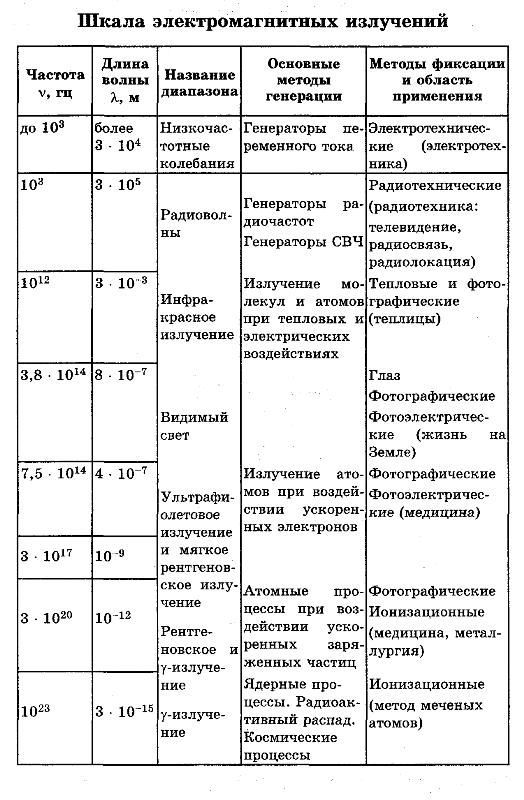
Электромагнитное излучение принято делить по частотам диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
3.6
Интерференция волн. Когерентные волны. Условия когерентности волн.
Оптическая длина пути (о.д.п.) света. Связь разности о.д.п. волн с разностью фаз колебаний, вызываемых волнами.
Амплитуда результирующего колебания при интерференции двух волн. Условия максимумов и минимумов амплитуды при интерференции двух волн.
Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей: а) красным светом, б) белым светом.
1) ИНТЕРФЕРЕНЦИЯ ВОЛН – такое наложение волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.
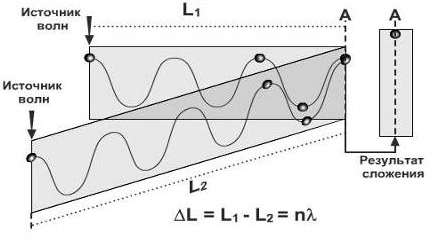
Необходимые условия для наблюдения интерференции:
1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);
2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).
Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе – пространственной когерентностью.
Дальше пример.
Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе).
Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление.
Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление.
Математически это выглядит так. Складываем две волны:
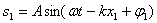
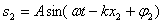
здесь х1 и х2 – расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:
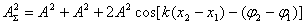
Максимум этого выражения есть 4A2, минимум – 0; всё зависит от разности начальных фаз и от так называемой разности хода волн :
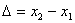
При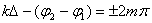 
в данной точке пространства будет наблюдаться интерференционный максимум, при 
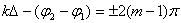– интерференционный минимум.
В нашем простом примере источники волн и точка пространства, где мы наблюдаем интерференцию, находятся на одной прямой; вдоль этой прямой интерференционная картина для всех точек одинакова. Если же мы сдвинем точку наблюдения в сторону от прямой, соединяющей источники, мы попадем в область пространства, где интерференционная картина меняется от точки к точке. В этом случае мы будем наблюдать интерференцию волн с равными частотами и близкими волновыми векторами.
2)1. Оптической длиной пути называется произведение геометрической длины d пути световой волны в данной среде на абсолютный показатель преломления этой среды n.
s=nd.
2. Разность фаз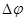 
двух когерентных волн от одного источника, одна из которых проходит длину пути 
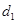в среде с абсолютным показателем преломления 
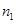, а другая – длину пути 
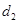в среде с абсолютным показателем преломления 
:
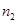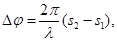
где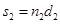 
, 
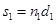, λ – длина волны света в вакууме.
3)Амплитуда результирующего колебания зависит от величины, называемой разностью хода волн.
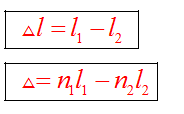
Если разность хода равна целому числу волн, то волны приходят в точку синфазно. Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой.
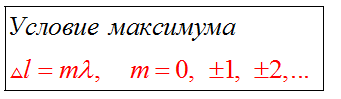
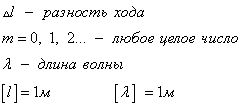
Если разность хода равна нечетному числу полуволн, то волны приходят в точку А в противофазе. В этом случае они гасят друг друга, амплитуда результирующего колебания равна нулю.
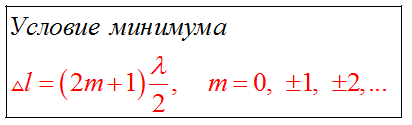
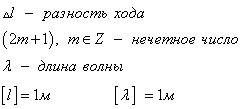
В других точках пространства наблюдается частичное усиление или ослабление результирующей волны.
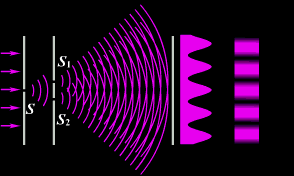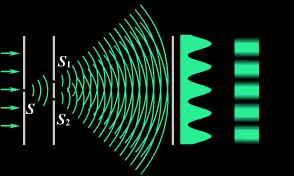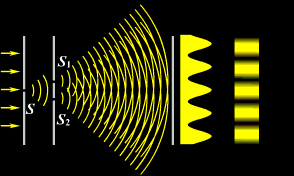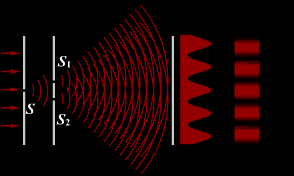
4)Опыт Юнга
В 1802 г. английский ученый Томас Юнг поставил опыт, в котором наблюдал интерференцию света. Свет из узкой щели S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок расширялся, и на белом экране световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
3.7
Осуществление интерференции света от обычных источников света.
Интерференция света на тонкой пленке. Условия максимумов и минимумов интерференции света на пленке в отраженном и в проходящем свете.
Интерференционные полосы равной толщины и интерференционные полосы равного наклона.
1)Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
2) 
интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной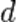 
, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 
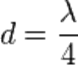, где 
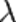— длина волны. Если 
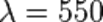нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от 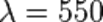нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
— условие максимума;
— условие минимума,
где k=0,1,2… и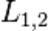 
— оптическая длина пути первого и второго луча, соответственно.
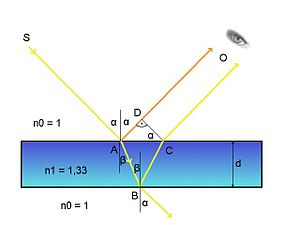
3)Полосы равного наклона
Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).
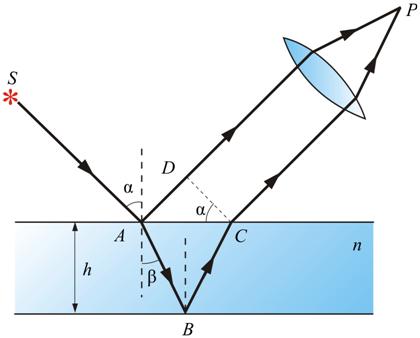
Рис. 8.8
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точкеP такая же, как на линии DC:
.
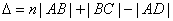Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е.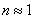 
. Так как 
, 
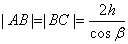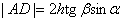(h – толщина пластинк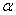и, 
и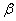 
– углы падения и преломления на верхней грани; 
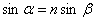), то для разности хода получаем
.
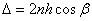Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
,
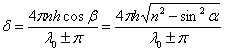где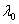 
– длина волны в вакууме.
В соответствии с последней формулой светлые полосы расположены в местах, для которых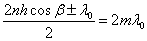 
, где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало 
посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает 
, а луч 2, отражаясь от з2 и далее от , дает 
. Пластинки и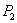 
одинаковы по размерам. 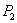ставится для компенсации разности хода второго луча. Луч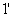и и 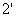когерентны и интерферируют.
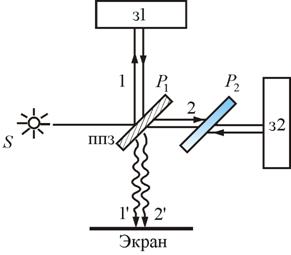
Рис. 8.9
§
Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).
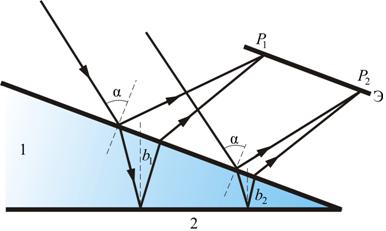
Рис. 8.10
Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).
Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.
Результат интерференции в точках 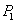и 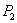экрана определяется по известной формуле 
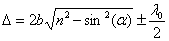, подставляя в неё толщину пленки в месте падения луча ( 
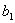или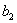 
). Свет обязательно должен быть параллельным ( 
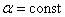): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.
Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
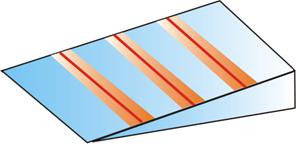
Рис. 8.11
3.8
Стоячая волна как частный случай интерференции. Уравнение плоской стоячей волны. Амплитуда стоячей волны. Узлы и пучности стоячей волны. Изменение вида стоячей волны со временем.
Превращения энергии в стоячей волне.
Образование стоячих волн в сплошных ограниченных средах. Условие их возникновения.
1)Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует
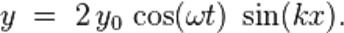
где:
· y0 — амплитуда волны,
· 
— циклическая (угловая) частота, измеряемая в радианах в секунду,
· k — волновой вектор, измеряется в радианах на метр, и рассчитывается как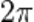 
поделённое на длину волны ,
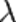· x и t — переменные для обозначения длины и времени.
Пучность — участок стоячей волны, в котором колебания имеют наибольшую амплитуду. Противоположностью пучности является узел — участок волны, в котором амплитуда колебаний минимальна.
Причиной пучности является сложение падающей и отраженной когерентных волн в «фазе», узел — сложение когерентных волн в «противофазе». При суперпозиции двух сигналов, близких по частоте и по амплитуде также образуются пучности и сужения.
2)Энергия в стоячей волне распределена так, что в областях, близких к узлам волны, сосредоточивается главным образом энергия потенциальная, а в областях, близких к пучностям волны, сосредоточивается энергия кинетическая. В тот момент времени, когда кинетическая энергия волны достигает максимума, потенциальная энергия становится минимальной. Через четверть периода максимума достигает энергия потенциальная, а энергия кинетическая убывает до нуля. Таким образом, в стоячей волне происходит непрерывное превращение и перераспределение энергии, но переноса энергии нет.
3)Собственные колебания таких систем связаны с образованием стоячих волн, особенности которых определяются условиями отражения на границах. Возбудить колебания в системе с распределёнными параметрами проще всего кратковременным воздействием, например ударом или щипком. Возникший волновой импульс «побежит» от места своего рождения во все доступные направления. В струне, к примеру, доступно одно лишь направление, по длине. Ввиду ограниченности области распространения колебаний, образовавшаяся волна, дойдя до границ колеблющегося тела, отразится и окажется, как бы «запертой» внутри ограниченного телом пространства. Прямые и отражённые волны, накладываясь, друг на друга, образуют стоячую волну. Параметры стоячей волны существенным образом зависят от условий отражения на границах. Стоячие волны не исчезают сразу после окончания возбуждения. Длительность существования стоячих вол зависит, прежде всего, от потерь, связанных с излучением энергии в окружающую среду и внутренним трением. Поскольку рассматриваемые колебания существуют после прекращения действия источника внешней силы, их относят к собственным колебаниям с затуханием.
3.9
Дифракция волн. Объяснение дифракции волн на основе принципа Гюйгенса – Френеля.
Дифракционная картина, наблюдаемая на плоском экране, если круглое отверстие освещается красным светом, и если между точечным источником красного света и экраном расположена круглая преграда.
1)Явление огибания волнами препятствий получило название дифракции. Для проявления дифракции размеры препятствий должны быть меньше или сравнимы с длиной волны.
Принцип Гюйгенса-Френеля
Каждый элемент поверхности, которой достигла в данный момент волна, является источником вторичных волн, распространяющихся в первоначальном направлении со скоростью исходной волны.
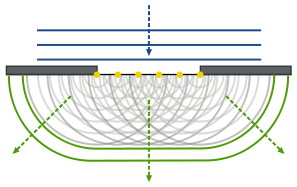
Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой. Согласно Френелю дифракция есть интерференция вторичных волн.
2) Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259).
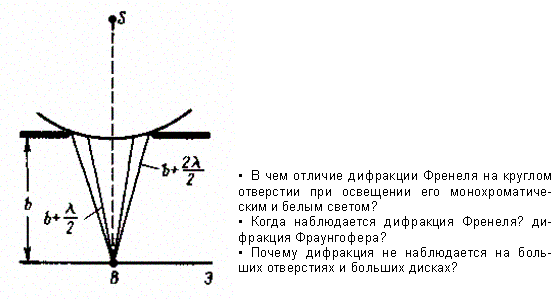
Рис. 259
Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),
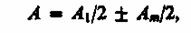
где знак плюс соответствует нечетным mи минус – четным m.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А1, т.е.вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (см. § 177). Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное – то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.
Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.
Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Am≪ A1и результирующая амплитуда A = A1/2,т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.
3.10
Дифракция Фраунгофера (дифракция в параллельных лучах), ее отличие от дифракции Френеля. Способы осуществления дифракции Фраунгофера.
Дифракция Фраунгофера от одной щели. Условия максимумов и минимумов дифракции. Распределение интенсивности света по экрану.
1)Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка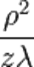 
, что сильно упрощает теоретическое рассмотрение явления. Здесь 
— расстояние от отверстия или преграды до плоскости наблюдения, 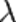— длина волны излучения, а 
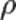— радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля 
, при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.
Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).
§
Размер ядра составляет 10^-14 – 10^-15 метров (следуя опытам Резерфорда).
Атомное ядро состоит из протонов – положительно заряженных частиц и нейтронов.
Атомное ядро характеризуется зарядом Z (равное числу протонов в атоме и совпадающее с порядковым номером х/э)
Радиоактивность – способность некоторых ядер самопроизвольно превращаться в другие ядра, испуская при этом радиоактивные излучения.
Р/излучение бывает трех типов: α, β и γ.
1)α-излучение характеризуется малой проникающей способностью и отклоняется электрическими и магнитными полями. Представляет собой поток ядер гелия.
2)β-излучение характеризуется большей проникающей способностью, но меньшей ионизирующей способностью. Представляет собой поток быстрых электронов.
)γ-излучение не отклоняется электрическими и магнитными полями, обладает слабой ионизирующей способностью, но большой способностью проникновения (при прохождении через кристаллы обнаруживает дифракцию). Представляет собой коротковолновое э/м излучение с чрезвычайно малой длиной волны, и, вследствие этого – ярко выраженными корпускулярными свойствами.
Радиоактивным распадом называют естественное превращение ядер, происходящее самопроизвольно.
dN = λNdt
λ – постоянная радиоактивного распада, или
N = N0e–λt
Из формулы следует, что число нераспавшихся ядер убывает со временем по экспоненциальному закону (закон полураспада – делим N и t на 2!).
Деление тяжелых ядер. В отличие от радиоактивного распада ядер, сопровождающегося испусканием α- или β-частиц, реакции деления – это процесс, при котором нестабильное ядро делится на два крупных фрагмента сравнимых масс.
В 1939 году немецкими учеными О. Ганом и Ф. Штрассманом было открыто деление ядер урана. Продолжая исследования, начатые Ферми, они установили, что при бомбардировке урана нейтронами возникают элементы средней части периодической системы – радиоактивные изотопы бария (Z = 56), криптона (Z = 36) и др.
Уран встречается в природе в виде двух изотопов: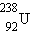 
(99,3 %) и 
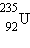(0,7 %). При бомбардировке нейтронами ядра обоих изотопов могут расщепляться на два осколка. При этом реакция деления 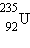наиболее интенсивно идет на медленных (тепловых) нейтронах, в то время как ядра 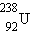вступают в реакцию деления только с быстрыми нейтронами с энергией порядка 1 МэВ.
Основной интерес для ядерной энергетики представляет реакция деления ядра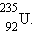 
В настоящее время известны около 100 различных изотопов с массовыми числами примерно от 90 до 145, возникающих при делении этого ядра. Две типичные реакции деления этого ядра имеют вид:
Обратите внимание, что в результате деления ядра, инициированного нейтроном, возникают новые нейтроны, способные вызвать реакции деления других ядер. Продуктами деления ядер урана-235 могут быть и другие изотопы бария, ксенона, стронция, рубидия и т. д.
Продукты деления ядра урана нестабильны, так как в них содержится значительное избыточное число нейтронов. Действительно, отношение N / Z для наиболее тяжелых ядер составляет примерно 1,6 (рис. 6.6.2), для ядер с массовыми числами от 90 до 145 это отношение порядка 1,3–1,4. Поэтому ядра-осколки испытывают серию последовательныхβ–-распадов, в результате которых число протонов в ядре увеличивается, а число нейтронов уменьшается до тех пор, пока не образуется стабильное ядро.
При делении ядра урана-235, которое вызвано столкновением с нейтроном, освобождается 2 или 3 нейтрона. При благоприятных условиях эти нейтроны могут попасть в другие ядра урана и вызвать их деление. На этом этапе появятся уже от 4 до 9 нейтронов, способных вызвать новые распады ядер урана и т. д. Такой лавинообразный процесс называется цепной реакцией
Термоядерные реакции. Второй путь освобождения ядерной энергии связан с реакциями синтеза. При слиянии легких ядер и образовании нового ядра должно выделяться большое количество энергии. Вплоть до ядер с массовым числом около 60 удельная энергия связи нуклонов растет с увеличением A. Поэтому синтез любого ядра с A < 60 из более легких ядер должен сопровождаться выделением энергии. Общая масса продуктов реакции синтеза будет в этом случае меньше массы первоначальных частиц.
Реакции слияния легких ядер носят название термоядерных реакций, так как они могут протекать только при очень высоких температурах. Чтобы два ядра вступили в реакцию синтеза, они должны сблизится на расстояние действия ядерных сил порядка 2·10–15 м, преодолев электрическое отталкивание их положительных зарядов. Для этого средняя кинетическая энергия теплового движения молекул должна превосходить потенциальную энергию кулоновского взаимодействия. Расчет необходимой для этого температуры T приводит к величине порядка 108–109 К. Это чрезвычайно высокая температура. При такой температуре вещество находится в полностью ионизированном состоянии, которое называется плазмой.
Энергия, которая выделяется при термоядерных реакциях, в расчете на один нуклон в несколько раз превышает удельную энергию, выделяющуюся в цепных реакциях деления ядер. Так, например, в реакции слияния ядер дейтерия и трития
§
Элемента́рная части́ца — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить (или пока это не доказано) на составные части. Их строение и поведение изучается физикой элементарных частиц. Понятие элементарных частиц основывается на факте дискретного строения вещества. Ряд элементарных частиц имеет сложную внутреннюю структуру, однако разделить их на части невозможно. Другие элементарные частицы являются бесструктурными и могут считаться первичными фундаментальными частицами.
Со времён первого открытия элементарной частицы (электрона) в 1897 году обнаружено уже более 400 элементарных частиц. Фундаментальные (бесструктурные) частицы:
лептоны — фермионы, которые имеют вид точечных частиц (т. е. не состоящих ни из чего) вплоть до масштабов порядка 10−18 м. Не участвуют в сильных взаимодействиях. Участие в электромагнитных взаимодействиях экспериментально наблюдалось только для заряженных лептонов (электроны, мюоны, тау-лептоны) и не наблюдалось для нейтрино. Известны 6 типов лептонов.
кварки — дробнозаряженные частицы, входящие в состав адронов. В свободном состоянии не наблюдались. Как и лептоны, делятся на 6 типов и являются бесструктурными, однако, в отличие от лептонов, участвуют в сильном взаимодействии.
калибровочные бозоны — частицы, посредством обмена которыми осуществляются взаимодействия:
фотон — частица, переносящая электромагнитное взаимодействие;
восемь глюонов — частиц, переносящих сильное взаимодействие;
три промежуточных векторных бозона W , W− и Z0, переносящие слабое взаимодействие;
гравитон — гипотетическая частица, переносящая г гравитационное взаимодействие. Существование гравитонов, хотя пока не доказано экспериментально в связи со слабостью гравитационного взаимодействия, считается вполне вероятным; однако гравитон не входит в Стандартную модель.
Фундаментальные взаимодействия. Процессы, в которых участвуют различные элементарные частицы, сильно различаются по энергиям и характерным временам их протекания. Согласно современным представлениям, в природе осуществляется четыре вида взаимодействий, которые не могут быть сведены к другим, более простым видам:сильное, электромагнитное, слабое и гравитационное. Эти виды взаимодействий называют фундаментальными.
Сильное (или ядерное) взаимодействие – наиболее интенсивное. Оно обуславливает исключительно прочную связь между протонами и нейтронами в ядрах атомов. В сильном взаимодействии могут принимать участие только тяжелые частицы – адроны (мезоны и барионы). Сильное взаимодействие проявляется на расстояниях порядка10–15 м и менее. Поэтому его называют короткодействующим.
Электромагнитное взаимодействие. В нем могут принимать участие любые электрически заряженные частицы, а так же фотоны – кванты электромагнитного поля. Электромагнитное взаимодействие ответственно, в частности, за существование атомов и молекул. Оно определяет многие свойства веществ в твердом, жидком и газообразном состояниях. Кулоновское отталкивание протонов приводит к неустойчивости ядер с большими массовыми числами. Электромагнитное взаимодействие обуславливает процессы поглощения и излучения фотонов атомами и молекулами вещества и многие другие процессы физики микро- и макромира.
Слабое взаимодействие – определяет ход наиболее медленных процессов, протекающих в микромире. В нем могут принимать участие любые элементарные частицы, кроме фотонов. Слабое взаимодействие ответственно за протекание процессов с участием нейтрино или антинейтрино, например, β-распад нейтрона
а также безнейтринные процессы распада частиц с большим временем жизни (τ ≥ 10–10 с).
Гравитационное взаимодействие присуще всем без исключения частицам, однако из-за малости масс элементарных частиц силы гравитационного взаимодействия между ними пренебрежимо малы и в процессах микромира их роль несущественна. Гравитационные силы играют решающую роль при взаимодействии космических объектов (звезд, планет и т. п.) с их огромными массами.
В 30-е годы XX века возникла гипотеза о том, что в мире элементарных частиц взаимодействия осуществляются посредством обмена квантами какого-либо поля. Эта гипотеза первоначально была выдвинута нашими соотечественниками И. Е. Таммом и Д. Д. Иваненко. Они предположили, что фундаментальные взаимодействия возникают в результате обмена частицами, подобно тому, как ковалентная химическая связь атомов возникает при обмене валентными электронами, которые объединяются на незаполненных электронных оболочках.
Взаимодействие, осуществляемое путем обмена частицами, получило в физике название обменного взаимодействия. Так, например, электромагнитное взаимодействие между заряженными частицами, возникает вследствие обмена фотонами – квантами электромагнитного поля.
Теория обменного взаимодействия получила признание после того, как в 1935 г. японский физик Х. Юкава теоретически показал, что сильное взаимодействие между нуклонами в ядрах атомов может быть объяснено, если предположить, что нуклоны обмениваются гипотетическими частицами, получившими название мезонов. Юкава вычислил массу этих частиц, которая оказалась приблизительно равной 300 электронным массам. Частицы с такой массой были впоследствии действительно обнаружены. Эти частицы получили название π-мезонов (пионов). В настоящее время известны три вида пионов: π , π– и π0 (см. табл. 6.9.1).
В 1957 году было теоретически предсказано существование тяжелых частиц, так называемых векторных бозонов W , W– и Z0, обуславливающих обменный механизм слабого взаимодействия. Эти частицы были обнаружены в 1983 году в экспериментах на ускорителе на встречных пучках протонов и антипротонов с высокой энергией. Открытие векторных бозонов явилось очень важным достижением физики элементарных частиц. Это открытие ознаменовало успех теории, объединившей электромагнитное и слабое взаимодействия в единое так называемое электрослабое взаимодействие. Эта новая теория рассматривает электромагнитное поле и поле слабого взаимодействия как разные компоненты одного поля, в котором наряду с квантом участвуют векторные бозоны.
5.1 Молекурярно-кинетические представления о строении вещества в различных агрегатных состояниях.
Статистический метод описания состояния и поведения систем многих частиц.
Распределение молекул идеального газа по состояниям.:
Тела, которые нас окружают (твердые, жидкие, газообразные) воспринимаются нашими органами чувств как сплошные. Однако, тела не сплошные, а состоят из мельчайших невидимых невооруженным глазом частичек, расположенных не вплотную друг к другу, а на некотором расстоянии. Называют эти мельчайшие частицы вещества молекулами (уменьшительное от латинского слова “масса”).
Демокрит (V в. до н. э.) назвал мельчайшие частицы, из которых состоят все тела в мире, атомами (неделимыми). Согласно Демокриту атомы имеют разные размеры, вес, форму и т.п
1) Все вещества состоят из мельчайших частиц – молекул. Молекула – наименьшая частица вещества, сохраняющая все его химические свойства. Все молекулы, образующие данное вещество, совершенно одинаковы. Молекулы состоят из атомов. Атом – мельчайшая частица химического элемента (105 шт.- 94 природных и 11 искусственных).
2) Между молекулами тела одновременно действуют силы взаимного притяжения и отталкивания.
3) Молекулы, образующие тела находятся в состоянии непрерывного беспорядочного движения (осцилляции).
Скорость движения молекул тем выше, чем выше температура тела. Температура – мера средней кинетической энергии молекул тела. Скорость движения молекул тела, определяющих кинетическую энергию, определяет тепловое состояние тела, величину его внутренней энергии. Хаотическое движение молекул называют тепловым.
Расщепление молекулы на атомы называется диссоциацией. Диссоциация происходит под действием 1) высокой температуры, 2) химических реакций, 3) облучения.
В основу термодинамики входят два метода исследования частиц: термодинамический и статический.
Поведение громадного числа молекул, составляющих макротела, изучается статистическим методом, который основан на том, что свойства макротел определяются свойствами молекул, особенностями их движения (скоростью, энергией, импульсом и т.д.) и взаимодействия. Например, температура может быть выражена через среднее значение кинетической энергии движения молекул. Статистический метод дает представление о механизме тепловых процессов, рассматривая их как бы изнутри макротел, он существенно дополняет термодинамический метод. Основные законы термодинамики также имеют статистический смысл.
В газе, находящемся в состоянии равновесия, установится некоторое стационарное (не меняющееся со временем) распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Такой закон был теоретически выведен Максвеллом.
При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что внешние поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Различают три формы записи распределения Максвелла.
5.2 Термодинамический метод описания состояния и поведения систем многих частиц.
Термодинамические параметры, их связь по средним значениям характеристик молекул:
Основное уравнение молекулярно-кинетической теории идеального газа, внутренняя энергия идеального газа, температура.
Для изучения тепловых процессов в естествознании сформировался термодинамический метод исследования. Он заключается в том, что термодинамическая система рассматривается как один целостный объект (а не как множество ее элементов, молекул), и ее состояние системы задается термодинамическими параметрами (параметрами системы), характеризующими ее свойства. В качестве таковых обычно выбирают абсолютную температуру(температуру по шкале Кельвина – Т), давление(Р), молярный объем (объем одного моля вещества – VМ). Параметры связаны друг с другом, поэтому состояние системы можно представить в виде уравнения. Например, для идеального газа массой в один моль эту связь выражает уравнение Менделеева-Клапейрона:
PVМ = RT, (5.1).где R = 8,314 Дж/моль * К – универсальная газовая постоянная.
ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ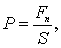 
где S – площадь этой поверхности; – сумма приложенных перпендикулярно сил. При неравномерном распределении сил по поверхности равенство определяет среднее давление на данную площадку, а в пределе, при стремлении S к кулю, – давление в данной точке:
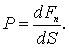По кинетической теории давление газа на стенки сосуда возникает в результате непрерывных ударов о них отдельных молекул. Эти удары молекул о стенки приводят к некоторым смешениям частиц материала стенки и, значит, к ее деформации. Деформированная же стенка действует на газ упругой силой, направленной в каждой точке перпендикулярно к стенке. Сила эта равна по абсолютному значению и противоположна по направлению силе, с которой газ действует на стенку.
Определение температуры в кинетической теории газов. В кинетической теории газов доказывается, что если две подсистемы (из одинаковых или разных молекул) могут обмениваться энергией, то в состоянии равновесия оказываются равными средние кинетические энергии поступательного движения их молекул. Исходя из этого, кинетическая теория газов определяет температуру как величину, пропорциональную средней кинетической энергии поступательного движения молекулы: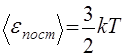
где k — постоянная Больцмана, которая выражается через универсальную газовую постоянную и число Авогадро (см. разд. 2.1): k = R/Na ~1,38•10 -23 Дж/К. Коэффициент пропорциональности выбран так, чтобы уравнение состояния идеального газа.
Внутренняя энергия данной массы идеального газа зависит только от его температуры и не зависит ни от давления, ни от объема.
5.3 Уравнение состояния идеального газа. Уравнения изопроцессов идеального газа.
Соотношение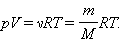 
называется уравнением состояния идеального газа. Для одного моля любого газа это соотношение принимает вид: pV=RT.
Изотермический процесс (T = const) Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. pV = const
Изохорный процесс (V = const)Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
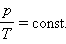
Изобарный процесс (p = const)Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.
5.4 Внутренняя энергия, способы ее изменения. Способы теплообмена. Количество теплоты. Первый закон термодинамики как закон сохранения энергии.
Газ, находящийся в состоянии термодинамического равновесия, можно характеризовать внутренней энергией. Внутренней энергией называют полную энергию его молекул. В термодинамике она включает в себя суммарную кинетическую энергию теплового движения молекул и потенциальную энергию их взаимодействия.
Существует два способа изменения внутренней энергии системы – механическая работа и теплопередача (теплообмен).
Процесс передачи энергии от одного тела к другому без совершения работы называется
теплообменом (теплопередачей).
Существует три вида теплообмена:
1. теплопроводность;
2. конвекция;
3. излучение.
Первый закон термодинамики – это закон сохранения энергии, распространенный на тепловые явления. Он показывает, от каких причин зависит изменение внутренней энергии.
термодинамике рассматриваются тела, положение центра тяжести которых практически не меняется. Механическая энергия таких тел остается постоянной, изменяться может лишь внутренняя энергия каждого тела.
В общем случае при переходе системы из одного состояния в другое внутренняя энергия изменяется одновременно как за счет совершения работы, так и за счет передачи теплоты.
Первый закон термодинамики формулируется именно для таких общих случаев:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Если система является изолированной, то работа внешних сил равна нулю (А = 0) и система не обменивается теплотой с окружающими телами (Q = 0). В этом случае согласно первому закону термодинамики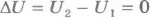 
или U1=U2. Внутренняя энергия изолированной системы остается неизменной (сохраняется).
Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой.
5.5 Работа газа, теплоемкость, изменение внутренней энергии, первый закон термодинамики при изопроцессах.
Работой газа называется его неквазистатическое расширение, а также последующее давление на определенную поверхность (как правило данный закон выполним для газа, находящегося в закрытом пространстве, например, поршне) под действием внешних сил.Теплоемкость– свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении.Газ, находящийся в состоянии термодинамического равновесия, можно характеризовать внутренней энергией.
Внутренней энергией называют полную энергию его молекул. В термодинамике она включает в себя суммарную кинетическую энергию теплового движения молекул и потенциальную энергию их взаимодействия.Закон Генри — закон, по которому при постоянной температуре растворимость газа в данной жидкости прямо пропорциональна давлению этого газа над раствором. Закон пригоден лишь для идеальных растворов и невысоких давлений. 
Собственно, закон Генри констатирует достаточно простой факт: чем выше давление газа над поверхностью жидкости, тем труднее растворенному в ней газу высвободиться. И это совершенно логично с точки зрения молекулярно-кинетической теории, поскольку молекуле газа, чтобы вырваться на свободу с поверхности жидкости, нужно преодолеть энергию соударений с молекулами газа над поверхностью, а чем выше давление и, как следствие, число молекул в приграничной области, тем сложнее растворенной молекуле преодолеть этот барьер.
§
Принцип равнораспределения энергии по степеням свободы молекул и теплоемкость идеальных газов при изопроцессах.
Количество теплоты.
Количеством теплоты (Q) называется изменение внутренней энергии тела, происходящее в результате теплопередачи. Количество теплоты всегда передается от более горячих тел к более холодным до достижения ими одинаковой температуры (теплового равновесия), если нет иных процессов, кроме теплопередачи.В замкнутой системе тел выполняется уравнение теплового балланса: Q1 Q2 … = 0 – количество теплоты, которое теряют горячие тела, равно количеству тепла, получаемому холодными.
Первый закон термодинамики(Q=ΔU A’)
Количество теплоты, переданное телу,
идет на изменение его внутренней энергии (ΔU)
и на совершение им работы(A’).
Теплоемкость.
ТЕПЛОЁМКОСТЬ -отношение подведенного к телу количества теплоты ΔQ к достигнутой при этом разности температур тела ΔT(кол-во теплоты,поглощаемой телом при нагревании):
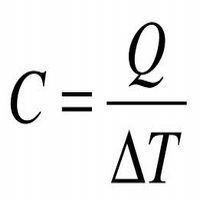
Удельная теплоемкость — это способность разных веществ к поглощению теплоты при их нагревании.
Удельная теплоемкость вещества определяется отношением количества теплоты, полученной им при нагревании, к массе вещества и изменению его температуры:
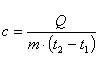
Молярная теплоемкость — количество теплоты, необходимое для нагревания 1 моль вещества на 1 К:
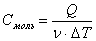
Принцип равнораспределения энергии по степеням свободы молекул.
В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2 , а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы:
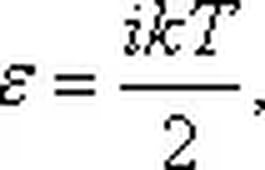
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i = iпост. iвращ. 2iколеб.
Закон равнораспределения показывает, что при тепловом равновесии, любая степень свободы (компоненты векторов положения или скорость частицы), которая появляется только как квадратичная функция в энергии, обладает средней энергией равной ½k в T и поэтому вносит вклад ½k в теплоёмкость системы.
Теплоемкость идеальных газов при изопроцессах.
1)Изохорический (изохорный) процесс– процесс изменения состояния газа, при котором объём газа остаётся постоянным: V=const.Для изохорического процесса:
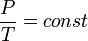
Работа газа при изохорном процессе равна нулю: А=0.
Все полученное тепло идет на изменение внутренней энергии в соответствии с первым началом термодинамики:
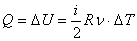
Молярная теплоемкость при изохорном процессе:
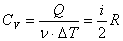
(Q-количество теплоты,c-удельная теплоемкость,M-молярная масса,i-количество степеней свободы,R-универсальная газовая постоянная,T-температура).
Изобарический (изобарный) процесс– процесс изменения состояния газа, при котором давление газа остаётся постоянным: р = const. Для изобарного процесса:
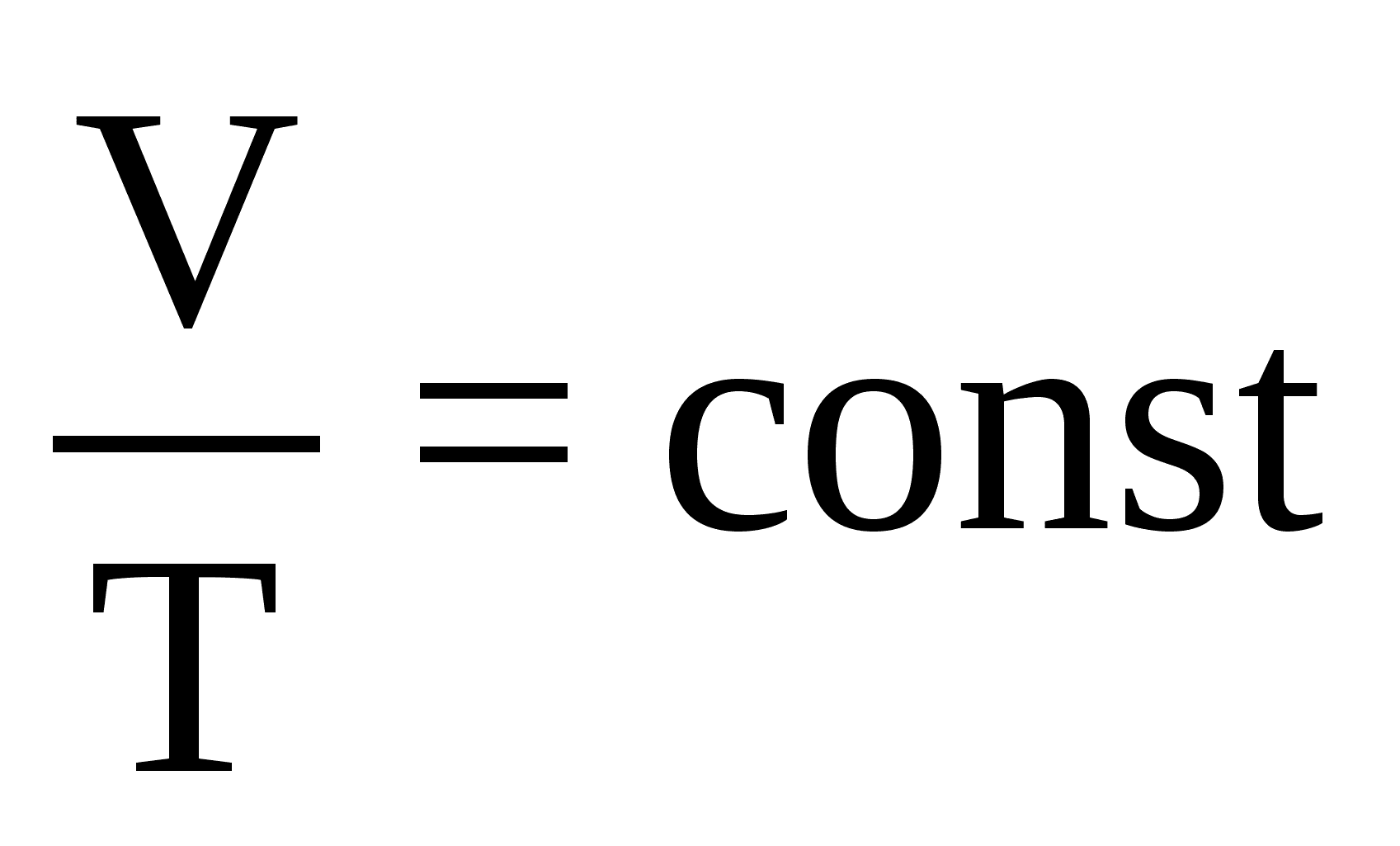
Работа газа при изобарном расширении:
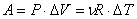
Изменение внутренней энергии:
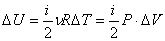
Количество полученного тепла в соответствии с первым началом термодинамики:
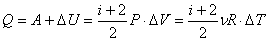
Молярная теплоемкость при изобарном процессе:
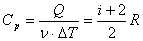
Изотермический процесс- процесс изменения состояния газа, при котором температура газа остаётся постоянным: Т = const. Для изотермического процесса:
PV=const
Работа газа при изотермическом расширении:
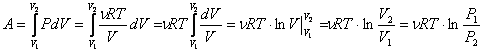
Изменение внутренней энергии при изотермическом процессе равно нулю:
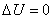
Все полученное тепло идет на совершение работы в соответствии с первым началом термодинамики:
