Измерение скорости потока жидкости. трубка пито
Всасывающее действие струи.
Горизонтальная трубка тока жидкости переменного сечения.
Наклонная трубка тока постоянного сечения.
V = const, тогда p1 rgh1 = p2 rh2g или p2 – p1 = rg(h1 – h2),
Dp = rgDh.
В этом случае, как и в гидростатистике, разность давлений обусловлена разностью весов соответствующих столбов жидкости.
Так как h1 = h2 (рис. 2) , то
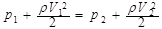 .
.
Полное давление в разных сечениях горизонтальной трубки тока одинаково. В более узких местах S2 < S1, V2 > V1, p2 < p1.
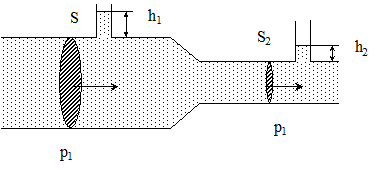
Рис. 2. Горизонтальная трубка тока жидкости переменного сечения.
Можно сделать столь узкое сечение трубки, что вследствие малого давления (ниже атмосферного) в это сечение будет засасываться воздух или жидкость (так называемое всасывающее действие струи). Это явление используют в водоструйных насосах, ингаляторах и пульверизаторах.
Выберем в движущемся потоке жидкости две точки 1 и 2, лежащие на одной линии тока (рис. 3).
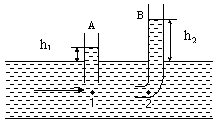
Рис. 3 Измерение скорости потока жидкости.
Так как трубка горизонтальная, а V2 = 0, то на основании формулы (7) запишем:
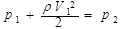 , откуда
, откуда  .
.
Трубку В, изображенную на рисунке 3 называют трубкой Пито. По высоте h2 столба жидкости в трубке Пито измеряют полное давление р2. Статическое давление р1 движущейся жидкости определяют при помощи трубки А по высоте h1 столба.
§
Образование атеросклеротической бляшки в артерии диаметром d1 вызывает сужение просвета артерии до диаметра d2 (рис.4).
Пусть артерия расположена горизонтально.
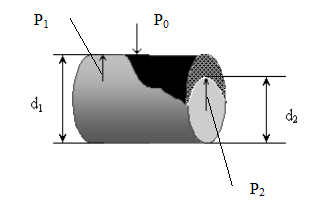
| Рис.4 Схема участка крупной артерии с атеросклеротической бляшкой. d1 – диаметр артерии, d2 – диаметр артерии в месте сужения, P0 – наружное давление, P1 – статическое давление внутри артерии, P2 – статическое давление внутри артерии в месте сужения. |
Течение крови по артерии будет происходить до того момента, пока статическое давление Р2 в месте образования атеросклеротической бляшки будет превышать наружное давление на сосуд Р0(его можно считать приблизительно равным атмосферному). То есть, кровоток возможен при условии:
Р2 – Р0 ³ 0.(8)
Это реализуется, если d2³ dmin.
Запишем уравнение Бернулли и условие неразрывности струи для нашего случая:
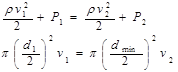 (9)
(9)
Откуда 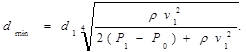 (10)
(10)
| Для сонной артерии: (нормальные условия) | средний диаметр d1= 1 cм, скорость крови v1 = 0,2 м/с, плотность крови r = 1,05 × 103 кг/м3, разница давлений Р1 – Р0 = 100 мм.рт.ст. = 1,33 × 104 Па |
Вычисленный по формуле 10 минимальный диаметр сонной артерии равен dmin » 2 мм.
Если диаметр сужения станет меньше dmin, тогда под действием внешнего давления Р0просвет сосуда в месте расположения атеросклеротической бляшки закроется и кровоток полностью остановится. Однако, в организме как в любой сложной системе существуют компенсационные механизмы. При сужении артерии сердце начинает работать в более напряженном режиме, в результате чего давление Р1в артерии начнет возрастать, и кровь с усилием протекает через сужение. С помощью фонендоскопа можно услышать прерывистый шум во время работы сердца, свидетельствующий о нарушении нормального кровотока.
§
Факторы, влияющие на вязкость крови в организме.
Разрыв аневризмы.
При некоторых патологиях наблюдается локальное снижение прочности и упругости кровеносных сосудов. Как следствие этого на некотором участке кровеносного сосуда его деформация под действием пульсирующего кровотока становится необратимой, и возникает вздутие сосуда (аневризма).
Скорость кровотока в месте развития аневризмы по условию неразрывности струи будет меньше, чем скорость кровотока в его недеформированной части. Согласно уравнению Бернулли, статическое давление в месте вздутия будет больше статического давления на участках сосуда нормального сечения. Нагрузка на расширенную часть сосуда увеличится, и возникшая аневризма под действием повышенного давления будет иметь тенденцию к расширению. В результате возможен разрыв аневризмы.
Вязкость крови в живом организме зависит, в основном, от скорости сдвига, свойств плазмы, относительного объема эритроцитов и механических свойств эритроцитов, температуры.
Скоростью сдвига называют величину градиента скорости движения параллельных слоев жидкости ( 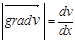 ). Вязкость крови зависит от скорости сдвига в диапазоне 0,1-120 с-1. При скорости сдвига>100 с-1 вязкость достигает значения асимптотической вязкости и при дальнейшем увеличении скорости сдвига (>200 с-1 ) не меняется (рис.10).
). Вязкость крови зависит от скорости сдвига в диапазоне 0,1-120 с-1. При скорости сдвига>100 с-1 вязкость достигает значения асимптотической вязкости и при дальнейшем увеличении скорости сдвига (>200 с-1 ) не меняется (рис.10).
При низких скоростях сдвига в крови эритроциты выстраиваются в монетные столбики. Это определяет высокую вязкость крови, которая, строго говоря, в этом случае не может рассматриваться как чистая жидкость. По мере увеличения скорости сдвига, агрегаты эритроцитов распадаются, и вязкость крови снижается, приближаясь постепенно к некоторому пределу. При высоких скоростях сдвига, например, в крупных артериях, кровь можно рассматривать как ньютоновскую жидкость. Только в этом случае кровь рассматривается как суспензия форменных элементов и ее свойства можно изучать in vitro на модели суспензии эритроцитов в физиологическом растворе.
Плазма.
Плазма ведёт себя как линейно-вязкая ньютоновская жидкость с относительной вязкостью 1,2. При рассмотрении течения в артериальных сосудах плазма принимается несжимаемой и вязкой с кинематической вязкостью 0,04 см2/с.
Неньютоновский характер крови обусловлен наличием форменных элементов крови, в основном, эритроцитов.
§
Ламинарное течение – упорядоченный режим течения вязкой жидкости, характеризующийся отсутствием перемешивания между слоями жидкости.
Течение жидкости с завихрениями называется турбулентным.
При малых скоростях течения случайно возникающие в потоке завихрения гаснут, не вызывая заметного перемешивания слоев. При высоких скоростях течения жидкости создаются условия, при которых течение перестает быть устойчивым и под влиянием случайных возмущений переходит в турбулентное.
Наличие условий, при которых ламинарное течение перестает быть устойчивым, зависит от числа Рейнольдса:
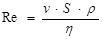 (25)
(25)
где v – скорость течения жидкости, S – сечение трубы, r – плотность жидкости, h – вязкость жидкости.
Как правило, значение критического числа Рейнольдса определяют экспериментально. Для гладких труб Reкр= 2300.
Если Reкр известно, то становится возможным для любой жидкости и разных условий ее течения предсказать, будет ли ее поток ламинарным или турбулентным. Если для определенного течения число Рейнольдса не превышает некоторого критического значения Reкр, ламинарное течение устойчиво. Если же Re > Reкр, то в потоке жидкости возникают завихрения – ее течение становится турбулентным.
Reкрдля крови равно 900¸1600. Движение крови в организме, в основном, ламинарное. Однако, при определенных условиях, кровоток может приобретать и турбулентный характер.
Турбулентность проявляется в полостях сердца (велико значение d), в аорте и вблизи клапанов сердца (высокая скорость движения крови). При интенсивной физической нагрузке скорость движения крови увеличивается, и это может вызвать турбулентность в кровотоке.
С уменьшением вязкости турбулентный характер течения жидкости может проявляться и при сравнительно небольшой скорости ее движения (см. формулу 25). Поэтому, при некоторых патологических процессах, приводящих к аномальному снижению вязкости крови, кровоток в крупных кровеносных сосудах может стать турбулентным.
Кровеносный сосуд не всегда можно моделировать гладкой трубой. В частности, при наличии атеросклеротических бляшек в просвете сосудов имеются локальные сужения, приводящие к возникновению турбулентности в течении крови. Турбулентность в кровотоке сопровождается шумами, прослушиваемыми с помощью фонендоскопа.
§
При сокращении сердца крупные кровеносные сосуды на некоторое время накапливают кровь. Кинетическая энергия выбрасываемой из сердца крови частично переходит в потенциальную энергию упругой деформации стенок аорты и крупных артерий. При диастоле проходит обратный процесс – потенциальная энергия деформированных артерий трансформируется в кинетическую энергию крови. Эластичные кровеносные сосуды как бы «дорабатывают» усилие сердца. Сердце является источником возбуждения колебаний давления на стенки кровеносных сосудов. Эти колебания распространяются по сосудистой системе, и возникающую при этом волну давления называют пульсовой волной.
Пульсовой волной называют волну повышенного давления, распространяющуюся по аорте и артериям, вызванную выбросом крови из левого желудочка в период систолы.
Пульсовая волна является затухающей волной. Происходит также сдвиг колебаний по фазе, который увеличивается с возрастанием расстояния от сердца до рассматриваемого участка сосудистой системы.
Пульсовая волна может быть представлена как сумма простых гармонических волн. Гармонический анализ пульсовых колебаний кровотока является одним из важных методов его изучения. Первая гармоническая составляющая пульсовой волны давленияможет быть записана в следующем виде:
Р1 = Ро е– ax sin w(t – x/v), (26)
где Ро – амплитуда пульсовых колебаний, t – время, х – расстояние от сердца до данной точки, w – циклическая (круговая) частота сердечных сокращений, v – скорость распространения пульсовой волны, a – коэффициент затухания, определяемый по характеристикам сосудистой системы.
Эластичность сосуда уменьшается с увеличением расстояния от сердца до периферии. Это обусловлено изменением относительного содержания эластина и коллагена в сосудистой ткани. С удалением от сердца увеличивается доля гладких мышечных волокон, которые в атрериолах являются уже основной составляющей сосудистой ткани.
Скорость распространения пульсовой волны в крупных кровеносных сосудах определяется по формуле Моенса-Кортевега:
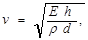 (27)
(27)
где Е – модуль упругости сосуда, h – толщина его стенки, d– диаметрсосуда. r – плотность крови.
Из формулы (27) следует: с увеличением жесткости сосуда и увеличением толщины его стенки скорость пульсовой волны возрастает.
В аорте она равна 4-6 м/с, в артериях мышечного типа – 8-12 м/с. Скорость распространения пульсовой волны намного больше линейной скорости кровотока, не превышающей в покое 0,5 м/с.
Поскольку с возрастом эластичность сосудов снижается (модуль упругости растет), то скорость пульсовой волны возрастает в 2-3 раза. Она растет и с увеличением давления. При повышенном давлении сосуд несколько растягивается, становится более «напряженным», и для его дальнейшего растяжения требуется большее усилие.
Форма пульсовых колебаний и их характеристики являются отражением работы сердца и состояния сосудистой системы.
Наряду с пульсовой волной в кровеносной системе распространяются и звуковые волны, скорость которых велика. Таким образом, в системе кровеносных сосудов выделяют три основных волновых процесса:
1. перемещение частиц крови (0,5 м/с),
2. распространение пульсовой волны (10 м/с),
3. распространение звуковых волн (1500 м/с).
§
Методы измерения давления крови.
В любой точке сосудистой системы давление крови зависит от:
а) атмосферного давления;
б) гидростатического давления pgh, обусловленного весом кровяного столба высотой h и плотностью р;
в) давления, обеспечиваемого насосной функцией сердца.
В соответствии с анатомо-физиологическим строением сердечно-сосудистой системы различают: внутрисердечное, артериальное, венозное и капиллярное кровяные давления.
Артериальное давление – систолическое (в период изгнания крови из правого желудочка) у взрослых людей в норме составляет 100 – 140 мм. рт. ст.; диастолическое (в конце диастолы) – 70 – 80 мм. рт. ст.
Показатели кровяного давления у детей с возрастом повышаются и зависят от многих эндогенных и экзогенных факторов (Таб. 3). У новорожденных систолическое давление 70 мм. рт. ст., затем повышается до 80 – 90 мм. рт. ст.
Таблица 3.
Артериальное давление у детей.
| Дети | Систолическое давление, мм.рт.ст. | Диастолическое давление, мм.рт.ст. |
| от 4 до 7 лет | 80 – 110 | 40 – 70 |
| от 8 до 13 лет | 90 – 120 | 50 – 80 |
| от 14 до 17 лет | 90 – 130 | 60 – 80 |
Разность давлений на внутреннюю (Рв) и наружную (Рн) стенки сосуда называют трансмуральным давлением(Рт): Рт = Рв – Рн.
Можно считать, что давление на наружную стенку сосуда равно атмосферному. Трансмуральное давление является важнейшей характеристикой состояния системы кровообращения, определяя нагрузку сердца, состояние периферического сосудистого русла и ряд других физиологических показателей. Трансмуральное давление, однако, не обеспечивает движение крови от одной точки сосудистой системы к другой. Например, среднее по времени трансмуральное давление в крупной артерии руки составляет около 100 мм.рт.ст. (1,33 . 104 Па). В то же время, движение крови из восходящей дуги аорты в эту артерию обеспечивается разностью трансмуральных давлений между указанными сосудами, которое составляет 2-3 мм.рт.ст. (0,03 . 104 Па).
При сокращении сердца величина давления крови в аорте колеблется. Практически измеряют среднее за период давление крови. Ее величина может быть оценена по формуле:
Рср» Рд (Рс Рд). (28)
Закон Пуазейля объясняет падение давления крови вдоль сосуда. Так, как гидравлическое сопротивление крови растет с уменьшением радиуса сосуда, то, согласно формуле 12, давление крови падает. В крупных сосудах давление падает всего на 15%, а в мелких – на 85%. Поэтому большая часть энергии сердца затрачивается на течение крови по мелким сосудам.
В настоящее время известны три способа измерения артериального давления: инвазивный (прямой), аускультативный и осциллометрический.
Иглу или канюлю, соединенную трубкой с манометром, вводят непосредственно в артерию. Основная область применения – кардиохирургия. Прямая манометрия – практически единственный метод измерения давления в полостях сердца и центральных сосудах. Венозное давление надежно измеряется так же прямым методом. В клинико-физиологических экспериментах применяется суточное инвазивное мониторирование артериального давления. Игла, введенная в артерию, промывается гепаринизированным солевым раствором с помощью микроинфузатора, а сигнал датчика давления непрерывно записывается на магнитную ленту.
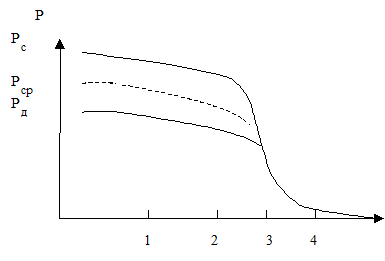
Рис.12. Распределение давления (превышение над атмосферным) в различных частях кровеносной системы: 1 – в аорте, 2 – в крупных артериях, 3 – в мелких артериях, 4 – в артериолах, 5 – в капиллярах.
Недостатком прямых измерений давления крови является необходимость введения измерительных устройств в полость сосуда. Без нарушения целостности сосудов и тканей осуществляется измерение давления крови с помощью инвазивных (непрямых) методов. Большинство непрямых методов являются компрессионными – они основаны на уравновешивании давления внутри сосуда внешним давлением на его стенку.
Простейшим из таких методов является пальпаторный способ определения систолического артериального давления, предложенный Рива-Роччи. При использовании данного метода на среднюю часть плеча накладывают компрессионную манжету. Давление воздуха в манжете измеряется с помощью манометра. При закачивании воздуха в манжету давление в ней быстро поднимается до значения, превышающего систолическое. Затем воздух из манжеты медленно выпускают, одновременно наблюдая за появлением пульса в лучевой артерии. Зафиксировав пальпаторно появление пульса, отмечают в этот момент давление в манжете, которое и соответствует систолическому давлению.
Из неинвазивных (непрямых) методов наибольшее распространение получили аускультативный и осциллометрический методы измерения давления.
§
Аукультативный метод имеет наибольшее распространение и основан на установлении систолического и диастолического давления по возникновению и исчезновению в артерии особых звуковых явлений, характеризующих турбулентность потока крови, – тонов Короткова. На область плеча накладывается компрессионная манжета. В манжету накачивается воздух до установления давления больше систолического. Давление, согласно закону Паскаля, передается на мягкие ткани и сосуды в глубине их. Артерия пережимается, кровь не течет и тоны Короткова не обнаруживаются. При выходе воздуха из манжеты давление, действующее на артерию, уменьшается. При равенстве наружного давления систолическому кровь начинает прорываться сквозь сдавленный манжетой участок артерии, и возникают характерные звуки, сопровождающие турбулентное течение крови и прослушиваемые с помощью фонендоскопа. В момент возникновения тонов по манометру определяют систолическое давление. Момент исчезновения шумов соответствует равенству измеряемого наружного давления диастолическому. Необходимо отметить, что систолическое и диастолическое давления только оцениваются, так как точно определяются по этому методу полное и статическое давления в кровеносном сосуде. Приборы, используемые для измерения давления крови, называют сфигмоманометрами.
Аускультативный метод реализуется в различных вариантах. В частности, в измерителях давления тоны Короткова могут восприниматься микрофоном, преобразующим звуковые воздействия в электрические сигналы, поступающие на регистрирующее устройство. На цифровом табло регистратора указываются значения систолического и диастолического давления. В некоторых приборах изменения в движении стенок артерии при систолическом и диастолическом давлении (сопровождающиеся возникновением и исчезновением тонов Короткова) определяются с помощью ультразвуковой локации и эффекта Доплера.
Осциллометрический метод. Метод основан на том, что при прохождении крови во время систолы через сдавленный участок артерии в манжете возникают микропульсации давления воздуха, анализируя которые можно получить значения систолического, диастолического и среднего давления. Систолическому давлению обычно соответствует давление в манжете, при котором происходит наиболее резкое увеличение амплитуды осцилляций, среднему – максимальный уровень осцилляций и диастолическому – резкое ослабление осцилляций.
Физические вопросы гемодинамики
Гемодинамикой называют область биомеханики, в которой исследуется движение крови по сосудистой системе. Физической основой гемодинамики является гидродинамика Течение крови зависит как от свойств крови, так и от свойств кровеносных сосудов
В главе рассматриваются также физические основы работы некоторых технических устройств, используемых в связи с кровообращением.
§
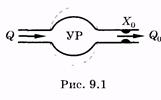 Рассмотрим гидродинамическую модель кровеносной системы, предложенную О. Франком. Несмотря на достаточную простоту, она позволяет установить связь между ударным объемом крови (объем крови, выбрасываемый желудочком сердца за одну систолу), гидравлическим сопротивлением периферической части системы кровообращения Х0 и изменением давления в артериях. Артериальная часть системы кровообращения моделируется упругим (эластичным) резервуаром (рис. 9.1, обозначено УР).
Рассмотрим гидродинамическую модель кровеносной системы, предложенную О. Франком. Несмотря на достаточную простоту, она позволяет установить связь между ударным объемом крови (объем крови, выбрасываемый желудочком сердца за одну систолу), гидравлическим сопротивлением периферической части системы кровообращения Х0 и изменением давления в артериях. Артериальная часть системы кровообращения моделируется упругим (эластичным) резервуаром (рис. 9.1, обозначено УР).
Так как кровь находится в упругом резервуаре, то ее объем V в любой момент времени зависит от давления р по следующему соотношению:
V = V0 kp, (9.1)
где k — эластичность, упругость резервуара (коэффициент пропорциональности между давлением и объемом), V0— объем резервуара при отсутствии давления (р = 0). Продифференцировав (9.1), получим
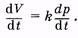 (9.2)
(9.2)
В упругий резервуар (артерии) поступает кровь из сердца, объемная скорость кровотока равна Q. От упругого резервуара кровь оттекает с объемной скоростью кровотока Q0 в периферическук систему (артериолы, капилляры). Предполагаем, что гидравлическое сопротивление периферической системы постоянно. Это моделируется «жесткой» трубкой на выходе упругого резервуара (рис. 9.1).
Можно составить достаточно очевидное уравнение (рис. 9.1)
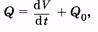 (9.3)
(9.3)
показывающее, что объемная скорость кровотока из сердца равна сумме скорости возрастания объема упругого резервуара и скорости оттока крови из упругого резервуара.
На основании уравнения Пуазейля (7.8) и формулы (7.9) можно записать для периферической части системы
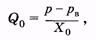 (9.4)
(9.4)
где р — давление в упругом резервуаре, рв— венозное давление, оно может быть принято равным нулю, тогда вместо (9.4) имеем
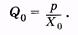 (9.5)
(9.5)
Подставляя (9.2) и (9.5) в (9.3), получаем
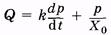 или
или 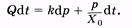 (9.6)
(9.6)
Проинтегрируем (9.6). Пределы интегрирования по времени соответствуют периоду пульса (периоду сокращения сердца) от 0 до Тп. Этим временным пределам соответствуют одинаковые давления — минимальное диастолическое давление рд:
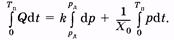 (9.7)
(9.7)
Интеграл с равными пределами равен нулю, поэтому из (9.7) имеем
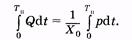 (9.8)
(9.8)
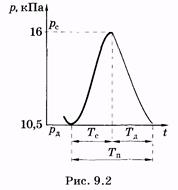 Экспериментальная кривая, показывающая временную зависимость давления в сонной артерии, приведена на рис. 9.2 (сплошная линия). На рисунке показан период пульса, длительности Тссистолы и Тд диастолы, рс— максимальное (систолическое) давление. Интеграл в левой части уравнения (9.8) равен объему крови, который выталкивается из сердца за одно сокращение, — ударный объем. Он может быть найден экспериментально. Интеграл в правой части уравнения (9.8) соответствует площади фигуры, ограниченной кривой и осью времени (см. рис. 9.2), что также можно найти. Используя указанные значения интегралов, можно вычислить по (9.8) гидравлическое сопротивление периферической части системы кровообращения.
Экспериментальная кривая, показывающая временную зависимость давления в сонной артерии, приведена на рис. 9.2 (сплошная линия). На рисунке показан период пульса, длительности Тссистолы и Тд диастолы, рс— максимальное (систолическое) давление. Интеграл в левой части уравнения (9.8) равен объему крови, который выталкивается из сердца за одно сокращение, — ударный объем. Он может быть найден экспериментально. Интеграл в правой части уравнения (9.8) соответствует площади фигуры, ограниченной кривой и осью времени (см. рис. 9.2), что также можно найти. Используя указанные значения интегралов, можно вычислить по (9.8) гидравлическое сопротивление периферической части системы кровообращения.
Во время систолы (сокращение сердца) происходит расширение упругого резервуара, после систолы, во время диастолы — отток крови к периферии, Q = 0. Для этого периода из (9.6) имеем
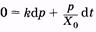 или
или 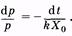 (9.9)
(9.9)
Проинтегрировав (9.9), получаем зависимость давления в резервуаре после систолы от времени:
 (9.10)
(9.10)
Соответствующая кривая изображена тонкой линией на рис. 9.2. На основании (9.5) получаем зависимость объемной скорости оттока крови от времени:
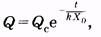 (9.11)
(9.11)
где 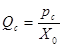 — объемная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).
— объемная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).
Зависимости (9.10) и (9.11) представляют собой экспоненты. Хотя данная модель весьма грубо описывает реальное явление, она чрезвычайно проста и верно отражает процесс к концу диастолы. Вместе с тем изменения давления в начале диастолы с помощью этой модели не описываются.
На основе механической модели по аналогии может быть построена электрическая модель (рис. 9.3).
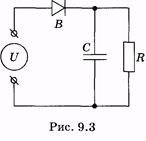
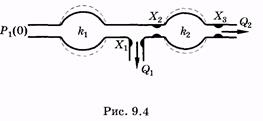
Здесь источник U, дающий несинусоидальное переменное электрическое напряжение, служит аналогом сердца, выпрямитель В — сердечного клапана. Конденсатор С в течение полупериода накапливает заряд, а затем разряжается на резистор R, таким образом происходит сглаживание силы тока, протекающего через резистор. Действие конденсатора аналогично действию упругого резервуара (аорты, артерии), который сглаживает колебание давления крови в артериолах и капиллярах. Резистор является электрическим аналогом периферической сосудистой системы. 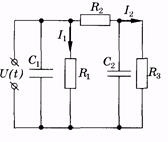 В более точной модели сосудистого русла использовалось большее количество эластичных резервуаров для учета того факта, что сосудистое русло является системой, распределенной в пространстве. Для учета инерционных свойств крови при построении модели предполагалось, что эластичные резервуары, моделирующие восходящую и нисходящую ветви аорты, обладают различной упругостью. На рис. 9.4 приведено изображение модели Ростона, состоящей из двух резервуаров с различными эластичностями (упругостями) и с неупругими звеньями разного гидравлического сопротивления между резервуарами. Этой модели соответствует электрическая схема, изображенная на рис. 9.5. Здесь источник тока задает пульсирующее напряжение U(t), являющееся аналогом давления p(t); емкости С1
В более точной модели сосудистого русла использовалось большее количество эластичных резервуаров для учета того факта, что сосудистое русло является системой, распределенной в пространстве. Для учета инерционных свойств крови при построении модели предполагалось, что эластичные резервуары, моделирующие восходящую и нисходящую ветви аорты, обладают различной упругостью. На рис. 9.4 приведено изображение модели Ростона, состоящей из двух резервуаров с различными эластичностями (упругостями) и с неупругими звеньями разного гидравлического сопротивления между резервуарами. Этой модели соответствует электрическая схема, изображенная на рис. 9.5. Здесь источник тока задает пульсирующее напряжение U(t), являющееся аналогом давления p(t); емкости С1
и С2 соответствуют упругостям резервуаров k1 и k2, электрические сопротивления Rv R2и R3— гидравлическим сопротивлениям Xlf X2и Х3, силы тока /j и /2 — объемным скоростям оттока крови Q1и Q2.
Такая модель математически описывается системой двух дифференциальных уравнений первого порядка, их решение дает
Рис. 9.5 две кривые, соответствующие первой и второй камерам.
Двухкамерная модель лучше описывает процессы, происходящие в сосудистом русле, но и она не объясняет колебания давления в начале диастолы.
Модели, содержащие несколько сотен элементов, называют моделями с распределенными параметрами.
§
Процессы теплообмена крайне важны для жизнеобеспечения. Поддержание постоянства температуры организма (так называемый температурный гомеостазис) является необходимым условием жизни человека (не случайно температура тела пациента служит врачу надежным показателем состояния здоровья). Поэтому все процессы, отображенные в уравнении теплового баланса, имеют в организме надежную регуляцию. Различают механизмы химической и физической терморегуляции.
Под химической терморегуляцией понимают возможность усиления или ослабления теплопродукции за счет изменения интенсивности окислительных процессов. Следовательно, химическая терморегуляция обеспечивается влияниями на обмен веществ (метаболизм). Поэтому теплопродукция в уравнении теплового баланса обозначена буквой М. Нужно заметить, что сам по себе метаболизм столь важен в организме, что изменять его в целях поддержания определенной температуры крайне нецелесообразно. Организм прибегает к химической терморегуляции только в особых случаях. В обычных условиях основным способом поддержания температурного гомеостазиса является физическая терморегуляция, то есть регуляция механизмов теплоотдачи: теплопроводности, конвекции, теплоизлучения, испарения.
Отметим еще раз, что теплообмен организма с окружающей средой происходит на поверхности тела. Как же осуществляется перенос тепловой энергии от внутренних органов и тканей к поверхности? Коэффициент теплопроводности тканей имеет низкое значение, поэтому роль теплопроводности в отведении тепловой энергии от внутренних органов к поверхности кожи и слизистых оболочек невелика Основное значение в этом процессе, а значит, в обеспечении терморегуляции внутренних органов принадлежит кровообращению.
Теплоемкость крови велика (такая же, как у воды), и нормальный кровоток достаточен для эффективного отвода тепла от внутренних органов к открытым поверхностям. Регуляция такого теплопереноса осуществляется главным образом за счет усиления или ослабления кровотока, то есть посредством сосудистых реакций. При необходимости отдать больше тепла кровеносные сосуды кожи и слизистых оболочек расширяются, что приводит к значительному увеличению массы циркулирующей в них крови, имеющей температуру глубоких тканей, а следовательно, и к возрастанию теплоотдачи. Для уменьшения теплоотдачи происходит сужение кожных сосудов.
У человека значительная потеря тепла происходит через кисти рук и стопы. Немудрено, что при переходе от холода к теплу кровообращение в руке человека усиливается в 30 раз, а в пальцах —в 600 раз.
У кроликов и зайцев важнейшим теплообменником служит ушная раковина, лишенная волосяного покрова на внутренней поверхности. У мелких грызунов — хвост, у птиц — конечности (особенно при погружении их в воду), у рогатых животных — рога (например, у коз около 12% тепла покидает организм через рога).
Из сказанного следует, что физическая терморегуляция является многофакторной системой, весьма эффективно обеспечивающей температурный гомеостазис(постоянство температуру организма). Многофакторность физической терморегуляции позволяет регулировать температуру тела в различных условиях: при исключении одних механизмов работают другие.
Например, у человека в состоянии относительного покоя при температуре внешней среды 293 К (суммарное теплообразование — M = ΣQi = 100 ккал-ч-1) роль разных путей теплообмена характеризуется следующими относительными величинами: теплопроведение — 0, конвекция—15%, радиация (теплоизлучение)— 66%, испарение—19%. Зная М, нетрудно рассчитать QT, QC , QR, QE Уравнению теплового баланса организма.
При тяжелой физической работе (М — 600 ккал-ч~’) и той же температуре соотношение вкладов разных способов теплоотдачи в температурный гомеостазис изменяется: теплопроведение— 0, конвекция—15%, радиация—12%, испарение — 75%.
При Tсреды>Tкожи , как уже говорилось, вся теплоотдача обеспечивается только одним механизмом — испарением воды с поверхности кожи (когда потоотделение недостаточно, можно поливать кожу водой).
Среди так называемых дополнительных механизмов терморегуляции нужно иметь в виду потери тепла на нагревание холодной пищи, а также теплопотери с мочой и калом. Их значение невелико Так, если съесть даже килограмм мороженого (его Т=273 К), то дополнительная теплоотдача составит всего около 50 ккал.
Наряду с химической и физической терморегуляцией, существенная роль в поддержании температурного гомеостазиса принадлежит теплоизоляции организма от внешней среды. Теплоизоляция осуществляется главным образом жировой тканью, шерстью на коже животных. Человек создал для этого одежду и жилища.
§
Тепловая энергия, образующаяся в организме, представляет собой конкретную форму связанной энергии биологической системы, так как в условиях жизнедеятельности она не может быть преобразована ни в одну из форм работ, совершаемых организмом. Чем же определяется связанная энергия?
Вспомним, что Wсвяз зависит от степени неупорядоченности молекулярного движения, а ее количественной мерой служит температура. Поэтому Wсвязпропорциональна Т. Однако величина связанной энергии в разных системах, имеющих одинаковую температуру, не всегда одинакова. Следовательно, степень неупорядоченности молекулярного движения зависит не только от температуры, но и от еще каких-то свойств системы. Эти свойства Клаузиус (1865) выразил в виде коэффициента, который однозначно связывает значения Wсвяз и Т. Коэффициент принято обозначать буквой s и называть энтропией. С вводом энтропии зависимость связанной энергии системы от ее температуры выглядит так:
Wсвяз= sT (1)
откуда
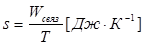 (2)
(2)
Энтропия — это физическая величина, характеризующая значение связанной энергии данной системы, приходящееся на единицу температуры (1 К).
Так как Wсвяз =sT, то выражение для внутренней энергии системы приобретает такой вид:
U=G sT ‘(3)
откуда
G = U-sT. (4)
Более строгое рассмотрение показывает, что эта формула справедлива только при постоянной температуре и постоянном объеме. В других условиях, например, при постоянной температуре, но изменяющемся объеме, выражение для свободной энергии имеет более сложный вид:
G = U — sT pV. (5)
Для изобарических процессов при постоянной температуре можно пользоваться формулой (4). В этом случае свободную энергию обычно обозначают буквой F и называют свободной энергией по Гельмгольцу, тогда как величину G, определяемую по формуле (5), принято называть свободной энергией по Гиббсу.
В; организме человека температура постоянна, а изменения объема, как правило, невелики. Поэтому при рассмотрении большинства жизненных процессов можно пользоваться понятием свободной энергии по Гельмгольцу (F). В биохимии зачастую рассматривают процессы, связанные с выделением или поглощением газов (кислород, углекислый газ и др.); так как объем газа при этом меняется, применяют понятие свободной энергии по Гиббсу (G).
Практический интерес представляет не сама по себе свободная энергия, а ее изменение. При V—const и T = const
ΔF=ΔU-TΔs (6)
Если объем изменяется, то изменение свободной энергии определяется по формуле
ΔG=ΔU-TΔs pΔV (7)
Говоря о запасе энергии в какой-либо системе, интересуются прежде всего тем, какую работу она может совершить. Ясно, что при этом следует учитывать не полную, а только свободную энергию. Пищевые продукты важны для человека потому, что он получает при их усвоении свободную энергию для совершения работы. В ванне горячей воды содержится больший запас энергии, чем в килограмме хлеба, но за счет ее организм, погруженный в ванну, не способен совершить работу, так как почти вся эта энергия является связанной.
Таким образом, энергия в различных формах имеет разную практическую ценность, которая тем выше, чем большую часть этой энергии можно преобразовать в работу, то есть чем меньше доля связанной энергии, мерой которой служит энтропия. Следовательно, чем ниже энтропия системы, тем выше ценность свойственной ей внутренней энергии.
Выше говорилось, что превращение свободной энергии в связанную называют диссипацией (рассеянием) энергии. Нетрудно понять, что таким превращением сопровождается любое преобразование более ценной формы энергии в менее ценную. Например, преобразование химической энергии, заключенной в биологических макромолекулах, в тепловую есть диссипация энергии.
Энтропия является функцией состояния системы. Это означает, что величина энтропии целиком определяется параметрами системы в данный момент и совершенно не зависит от ее «истории», то есть от того, как система пришла в данное состояние. Функцией состояния являются и некоторые другие физические величины, например, потенциальная энергия: ее значение зависит только от высоты, на которую поднято тело, но не от того, каким путем оно достигло этой высоты. А вот количество тепла не является функцией состояния системы: зная, например, что литр воды находится при температуре 303 К, мы ничего не можем сказать о том, какое количество тепла получила или отдала вода. Чтобы ответить на этот вопрос, нужно знать, во-первых, исходное состояние и, во-вторых, как именно протекал процесс изменения температуры, в частности, совершалась при этом работа или нет.
Рассмотрим теперь как практически можно вычислить значение энтропии. Согласно положениям термодинамики, изменение энтропии при элементарном обратимом процессе определяется выражением
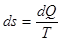 (8)
(8)
или, при обратимом переходе из некоторого состояния (1) в состояние (2):
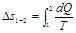
Может показаться, будто эти формулы не имеют практического значения, поскольку все реальные процессы необратимы. Однако ими успешно пользуются и практических расчетах. Дело в том, что Δs1–2 всегда одно и то же, независимо от процесса, посредством которого осуществлен переход системы (1) в состояние (2), так как энтропия — функция состояния. Поэтому расчеты, проведенные применительно к обратимому процессу, оказываются правильными и для необратимого процесса, но их гораздо проще выполнять.
Найдем, например, изменение энтропии при нагревании воды от 293 К до 373 К Это необратимый процесс, Так как в ходе его неизбежны потери энергии за счет утечки тепла в окружающую среду, создания конвекционных потоков и т. д. Однако при вычислении энтропии этим можно пренебречь и использовать формулы, отображающие изменения энтропии при обратимом процессе:

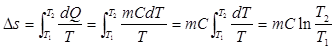
где С — удельная теплоемкость воды. Подставляя числа, получаем:
Δs=1 кг 4180 Дж кг-1 К-1 ln (373/293)≈1220 Дж К-1 (10)
Так как энтропия — функция состояния, то изменение энтропии будет таким же и в реальном необратимом процессе, хотя затраченное количество тепла будет фактически больше, чем при обратимом процессе.
Зная изменение энтропии, легко подсчитать изменение свободной энергии системы как по Гельмгольцу, так и по Гиббсу (формулы 4, 5).
При выяснении понятия энтропии учащиеся нередко задают вопрос: есть ли смысл вводить это понятие, если энтропия выражается через Q и Т, не проще ли прямо выражать свободную энергию через количество тепла? Такой вопрос возникает лишь в том случае, если не учитывать, что количество тепла, которое система получила или отдала, сильно зависит от способа перехода ее из одного состояния в другое, тогда как энтропия как функция состояния не зависит от этого. Поэтому на практике проще вычислить изменение энтропии. Такой расчет позволяет отвлечься от протекания процесса и учитывать только начальное и конечное состояние системы.
Кроме того, понятие энтропии имеет огромное теоретическое значение. Энтропия является физической величиной, количественно характеризующей те особенности молекулярного строения системы, от которых зависят энергетические преобразования в ней, в частности их направление (греческое слово εντρωπα переводится на русский язык как превращение, развитие, эволюция, поворот). Эту связь энтропии с молекулярной структурой системы понял Л. Больцман, установивший ее статистический смысл.







