.
установка специальных сужающих устройств
. Способ крепления сужающего устройства
должен обеспечивать возможность периодического осмотра с целью проверки
соответствия его требованиям настоящих методических указаний.
. Сужающее устройство необходимо
устанавливать концентрично оси трубы. Кратчайшее расстояние l
между осью сужающего устройства и осью трубы определяют по формуле
8.3. Значения внутреннего диаметра
трубопровода (D), соответствующие рабочей температуре t вещества, определяют по формуле
= D20 [l α΄t (t – 20)] = D20k΄t, ()
где α΄t
– средний коэффициент линейного теплового расширения металла трубопровода.
Действительный
внутренний диаметр участка трубопровода перед сужающим устройством вычисляют
как среднее арифметическое результатов измерений в двух поперечных сечениях:
непосредственно у сужающего устройства и на расстоянии 2 Dот него.
При этом в каждом из сечений измерения
проводятся не менее, чем в четырех диаметральных направлениях. Отклонение действительного
диаметра Dот его расчетного значения находят по
формуле
где ![]() выбирается из
выбирается из
требований к погрешности измерений расхода в пределах от 0,05 до 0,3 %. При
этом значение выбранной величины ![]() необходимо учитывать в
необходимо учитывать в
формуле (5.2).
Диаметр трубы после сужающего устройства по длине 2 Dможет отличаться от диаметра трубы перед ним, но
не более чем на ±2 %.
Измерительный
участок трубопровода должен быть прямым, цилиндрическим с круглым сечением, на
внутренней поверхности участка трубопровода перед сужающим устройством и за ним
не должно быть никаких уступов, а также заметных невооруженным глазом наростов
и неровностей от заклепок, сварных швов и так далее.
Результаты
отдельных измерений диаметра в двух различных плоскостях (на расстоянии 2 D и непосредственно перед сужающим
устройством) и четырех диаметральных направлениях не должны отличаться более
чем на ±0,3 % от среднего значения D20
Внутреннее сечение прямых участков трубопровода, расположенных далее чем на 2 Dот сужающего устройства, считается круглым, если
оно кажется таковым при визуальном осмотре.
Специальные
сужающие устройства допускаются к применению только на гладких трубопроводах.
Трубопровод считается гладким, если средняя относительная шероховатость Ra / D
прямого участка длиной 10 Dдо сужающего устройства не превышает
следующих значений:
т Ra / D
· 104 m Ra / D
· 104
,09 25,0 0,2 5,6
,10 18,1 0,25 4,9
,12 12,9 0,36 4,2
,13 10,0 0,49 4,0
,14 8,3 0,64 3,9
,16 7,1
. Установка специального сужающего
устройства непосредственно у местных сопротивлений не допускается.
Необходимые минимальные длины прямых
участков трубопровода (L1/D) до сужающих устройств
Группа колен или смешивающиеся потоки | Задвижка | Запорный вентиль | Кран | Шаровой клапан | Гильза термометра | ||||
0,03 D£d* | d* £ 0,03 D | ||||||||
в разных плоскостях | в одной плоскости | ||||||||
0,05 | 34 | 14 | 12 | 50 | 20 | 18 | 15 | 5 | |
0,10 | 34 | 16 | 12 | 50 | 20 | 18 | 15 | 5 | |
0,15 | 36 | 17 | 12 | 50 | 20 | 19 | 15 | 5 | |
0,20 | 38 | 18 | 12 | 60 | 20 | 20 | 15 | 5 | |
0,25 | 40 | 20 | 12 | 60 | 30 | 22 | 15 | 5 | |
0,30 | 44 | 22 | 14 | 60 | 30 | 24 | 15 | 5 | |
0,35 | 47 | 26 | 14 | 60 | 30 | 26 | 15 | 5 | |
0,40 | 52 | 30 | 15 | 60 | 30 | 28 | 15 | 5 | |
0,45 | 57 | 33 | 18 | 60 | 40 | 30 | 15 | 5 | |
0,50 | 63 | 37 | 20 | 60 | 40 | 33 | 20 | 5 | |
0,55 | 69 | 41 | 24 | 60 | 40 | 36 | 20 | 5 | |
0,60 | 75 | 45 | 27 | 60 | 50 | 40 | 20 | 5 | |
0,65 | 80 | 50 | 30 | 60 | 60 | 44 | 20 | 5 | |
* Диаметр гильзы термометра.
Регулирующий вентиль Н – степень открытия | Регулирующий клапан H – степень | Регулировочная заслонка | Колено или тройник | |||||||
H = 0,25 | H = 0,50 | H = 0,75 | H = 1,00 | H = 0,25 | H = 0,50 | H = 0,75 | H = 1,00 | |||
0,05 | 30 | 30 | 30 | 20 | 20 | 15 | 15 | 15 | 30 | 10 |
0,10 | 40 | 30 | 30 | 20 | 25 | 20 | 15 | 15 | 30 | 10 |
0,15 | 40 | 40 | 30 | 20 | 25 | 20 | 15 | 15 | 35 | 14 |
0,20 | 50 | 40 | 30 | 20 | 30 | 25 | 20 | 15 | 35 | 14 |
0,25 | 60 | 40 | 30 | 30 | 35 | 25 | 20 | 20 | 40 | 14 |
0,30 | 60 | 50 | 40 | 30 | 35 | 30 | 25 | 20 | 40 | 16 |
0,35 | 70 | 50 | 40 | 30 | 40 | 30 | 25 | 20 | 40 | 18 |
0,40 | 70 | 60 | 40 | 30 | 45 | 35 | 25 | 20 | 40 | 21 |
0,45 | 70 | 60 | 40 | 30 | 45 | 35 | 30 | 25 | 40 | 24 |
0,50 | 80 | 60 | 50 | 30 | 45 | 35 | 30 | 25 | 45 | 29 |
0,55 | 80 | 60 | 50 | 40 | 50 | 40 | 30 | 25 | 45 | 35 |
0,60 | 80 | 70 | 50 | 40 | 50 | 40 | 30 | 25 | 50 | 40 |
0,64 | 80 | 70 | 50 | 40 | 50 | 40 | 35 | 30 | 50 | 46 |
Устройства, создающие закрутку потока (угол | Диафрагма с относительной площадью | Внезапное расширение со степенью | Диффузор с углом расширения от 30 до 55° | Конфузор с углом сужения от 35 до 70° | |||
φ = 30° | φ = 45° | φ = 60° | |||||
0,05 | 60 | 70 | 60 | 15 | 60 | 16 | 5 |
0,10 | 60 | 70 | 70 | 15 | 60 | 16 | 5 |
0,15 | 70 | 80 | 70 | 15 | 60 | 16 | 5 |
0,20 | 70 | 80 | 80 | 20 | 70 | 17 | 5 |
0,25 | 70 | 80 | 80 | 20 | 70 | 18 | 6 |
0,30 | 80 | 90 | 90 | 20 | 70 | 20 | 8 |
0,35 | 80 | 90 | 90 | 25 | 80 | 22 | 9 |
0,40 | 80 | 90 | 100 | 25 | 80 | 24 | 10 |
0,45 | 80 | 90 | 100 | 25 | 80 | 27 | 13 |
0,50 | 90 | 90 | 100 | 25 | 80 | 31 | 15 |
0,55 | 90 | 100 | 100 | 25 | 80 | 37 | 20 |
0,60 | 90 | 100 | 110 | 25 | 90 | 45 | 25 |
0,65 | 90 | 100 | 110 | 30 | 90 | 54 | 30 |
В табл. 6 – 8 представлены значения необходимых
минимальных длин прямых участков трубопровода после различных местных
сопротивлений. Для местных сопротивлений, не приведенных в этих таблицах, длину
прямого участка определяют по рис. 12.
Регулирующую
трубопроводную арматуру необходимо устанавливать за сужающим устройством.
Если
ближайшим к сужающему устройству местным сопротивлением является емкость с
внутренним диаметром не менее 10 Dи длиной не менее 20 D, то
при выборе прямого участка, расположенное перед емкостью местное сопротивление
не учитывается.
Если перед сужающим устройством последовательно расположено
несколько местных сопротивлений, то длина прямого участка определяется двумя
последними местными сопротивлениями. Расстояние между сужающим устройствам и
ближайшим к нему местным сопротивлением находят по табл.
Необходимые длины прямых участков между двумя
ближайшими к сужающему устройству местными сопротивлениями
Длина прямого | ||
Группа колен в | 17,5 | |
Группа колен в | 30 | |
Колено или | 15 | |
Сужение при | 7,5 | |
Внезапное | 40 | |
Устройства, | ||
φ = 30° | 45 | |
φ = 45° | 45 | |
φ = 60° | 50 | |
Диафрагма с относительной | 12,5 | |
Симметричный | 12,5 | |
Расширение при | 12,5 | |
Гильза | 10 | |
d* | 2,5 | |
Шаровой клапан | 15 | |
Кран | 20 | |
Задвижка | 10 | |
Запорный | 16 | |
Регулировочный | 40 | |
0,50 | 30 | |
0,75 | 25 | |
1,00 | 15 | |
Регулировочный клапан 0,25 | 22,5 | |
0,50 | 17,5 | |
1,00 | 12,5 | |
Регулировочная | 22,5 |
Для промежуточных значений mдлина прямого участка трубопровода перед
сужающим устройством выбирается по ближайшему наибольшему значению m, приведенному
в табл. 6
– 8.
Необходимые
наименьшие длины прямых участков (L2)
трубопровода за сужающим устройством указаны ниже:
m L2 / D
,05 4,0
,20 6,0
,40 7,0
,60 8,0
Глава 7. техника измерения расхода
– нефтемагнат
Глава 7. ТЕХНИКА ИЗМЕРЕНИЯ
РАСХОДА
7.1. Расходомеры
переменного перепада давления.
Принцип действия. Уравнения
измерений
Принцип действия
расходомеров данного типа, объединенных
единым методом измерений, основан на
измерении перепада давления, образующегося
в результате местного изменения скорости
потока жидкости, газа или пара.
*
Метод переменного перепада
давления один из наиболее старых и
изученных методов измерения расхода. Это, а
также возможность косвенной градуировки и
поверки стандартизованных первичных
преобразователей — сужающих устройств,
реализующих метод, их простота и
надежность, серийный выпуск вторичных
преобразователей — дифманомет-ров
обусловило его чрезвычайно широкое
(преимущественное по сравнению с другими)
использование в практике промышленных
измерений расхода. И вместе с тем в основе
этого чисто гидродинамического метода
лежат столь сложные физические процессы
деформации потоков, столь большое число
неконтролируемых факторов влияет на
характер этих процессов, что применение его
в настоящее время ограничено областями, где
требуется относительно низкая точность
измерений, хотя возможности его
„метрологического совершенствования”
далеко не исчерпаны.

Рассмотрим идеальную
физическую картину явлений, лежащих в
основе метода измерения расхода по
перепаду давления на сужающем
устройстве.
На рис. 55 показана форма
потока несжимаемой жвдкости, протекающей
через диафрагму. Выделим в трубопроводе два
сечения: /-/ — перед сужающим устройством
там, где поток еще не меняет своей
конфигурации, и II—П — в месте
наибольшего сжатия потока, находящемся на
некотором расстоянии от внешнего (по ходу
потока) торца диафрагмы.
Обозначим
F — площадь поперечного
сечения трубопровода, м2;
F0— площадь отверстия
диафрагмы, м2; m=F0/F
— относительная площадь
сужающего устройства; Fl — площадь
сечения потока в месте его наибольшего
сжатия, м2.
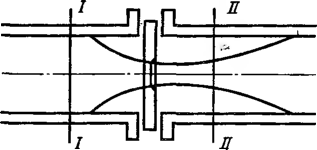
Рис.
55. Форма потока жидкости, протекающей через
диафрагму
Для сечений I I и II— П
горизонтального установившегося потока
несжимаемой жидкости плотностью р
уравнение Бернулли будет иметь
вид
Ру ср2
Р»ср,
2—2–(7-1)
а
уравнение неразрывности
Fvcp,
~Fivcp2 ~ № ^o^cpj
> (7-2)
где ii —
Fi/F0 — коэффициент сжатия потока,
зависящий от вида сужающего устройства;
vcpj и vcPz — средние скорости
потока в сечениях I—I и //-//
соответственно; рх и р2
— абсолютные давления в
сечениях
I—I и II—II
соответственно.
Решая совместно
уравнения (7.1) и (7.2), получим выражение для
средней скорости потока в сечении
II-II
V1 – (ti)2m2
При
течении реальных измеряемых сред возникают
дополнительные (не учтенные в приведенных
выше формулах) физические явления,
например, потери давления на вязкостное
трение, вихревые сопротивления,
неравномерное распределение скоростей,
изменение плотности и т. п.
Учитывая
эти обстоятельства, а также несовпадение
мест реального отбора давлений с базовыми
сечениями /—/ и II—П (обычно перепад
давления измеряется в углах, образованных
стенками трубы с торцами диафрагмы) , для
получения уточненных общих уравнений
расхода правые части формул (7.5) и (7.6)
умножают на скоростной коэффициент ?,
характеризующий распределение скоростей
по сечению выходящего из сужающего
устройства потока, и коэффициент е,
учитывающий изменение плотности потока
газа или пара при течении через сужающее
устройство.

Тогда уравнения расхода
приобретают
вид Q = aeF0 у/ ~
где а
¦
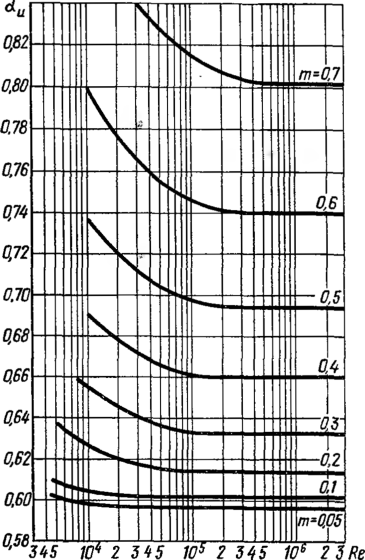
Рис. 56. Графики изменения исходных
коэффициентов расхода нормальных
диафрагм
(Р1-Р2); (7.7)
М =
ae]<(lf2р(pi-pi) , (7.8) м’
Г
V 1 – (д’)2тг
Эти уравнения являются
общими для всех расходомеров переменного
перепада давления и пригодными для
сжимаемой и несжимаемой сред. Для
несжимаемой среды е= 1.
Коэффициент
а, входящий в уравнения (7.7) и (7.8),
называется коэффициентом расхода. Этот
коэффициент зависит от относительной
площади т сужающего устройства. С
его помощью учитывают сложные
гидродинамические явления, происходящие в
потоке при изменении его
конфигурации.
Не принимая во внимание
действие сил тяжести на поток (при течении
измеряемой среды по трубе с дозвуковыми
скоростями такая идеализация допустима), на
основании соображений, приведенных в
предыдущей главе, можно утверждать, что
явления, происходящие в установившемся,
слабо пульсирующем и невращающемся потоке,
однозначно определяются критерием подобия
Рейнольдса. А если это так, то и коэффициент
а, учитывающий эти явления,
функционально зависит от числа
Рейнольдса.
На рис. 56 показаны графики
изменения исходных (для условий
установившегося, не пульсирующего и не
вращающегося потока, при отсутствии
близко расположенных местных
сопротивлений) коэффициентов расхода
нормальных диафрагм для различных значений
т в зависимости от чисел
Рейнольдса.
Как видно из рисунка,
коэффициенты расхода остаются постоянными
для одних и тех же т при Re, больших
некоторых предельных значений Re^, т. е. там
поток приобретает автомодельный характер.
Наличие автомодельной области (Re
> Renp) позволяет градуировать
сужающие устройства, для которых
составлены таблицы значений а
косвенным расчетным
методом.
Естественно, если условия,
при которых определены а, изменяются в
процессе эксплуатации расходомера с
сужающим устройством (например, если
появляются существенные пульсации или
вращательное движё-ние потока, нет
достаточных длин прямых участков перед
расходомером) , то исходные коэффициенты
расхода необходимо корректировать, вводя
соответствующие поправки или внося
коррективы на точность измерений
расхода.
Как следует из уравнений (7.7)
и (7.8), расход (QилиМ) и перепад
давления (Др — Pi – Р2)
функционально связаны квадратичной
параболической зависимостью. Отсутствие
линейной пропорциональности между
объектом измерения (Др) и измеряемым
параметров (Q или М) является
основным методическим недостатком
расходомеров переменного перепада
давления.
Из приведенных выше
методических предпосылок следует, что для
измерения расхода жидкостей, газов и паров
по перепаду давления необходимы три
устройства, объединенные общим понятием
расходомер переменного
перепада:
устройство, создающее
перепад давления в потоке измеряемой среды
за счет местного изменения скорости потока
или по значению (сужающие устройства), или
по направлению (изогнутые участки
трубы);
измерительный прибор —
дифманометр, измеряющий перепад
давления;
соединительное
устройство, передающее перепад давления от
потока к дифманометру.
Иногда к ним
добавляются еще вторичный преобразователь,
преобразующий показания дифманометра в
электрический, пневматический или
частотный сигнал, и вторичный прибор для
регистрации этого
сигнала.
Стандартные типы сужающих
устройств. В настоящее время наиболее
распространены стандартные сужающие
устройства трех типов: нормальная
диафрагма, нормальное сопло и труба (сопло)
Вентури.
Нормальная
диафрагма. При угловом отборе
давления применяют нормальные диафрагмы
двух видов — плоские (рис. 57) и камерные (рис.
58).
Нормальная диафрагма
представляет собой тонкий диск с
отверстием, концентричным оси трубы, с
острой прямоугольной кромкой со стороны
входа потока.
I
Рис. 57. Плоская
диафрагма
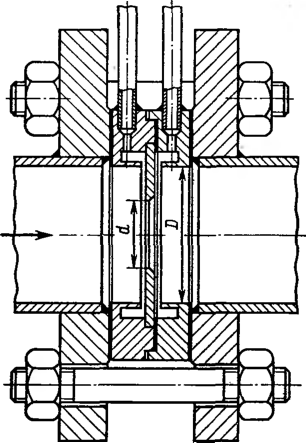
Рис.
58. Камерная диафрагма
Соосность установки, диафрагмы,
острота входной кромки, формирующей
определенный характер течения измеряемой
среды через отверстие диафрагмы , ее
прямоугольность и технологический допуск
на входной диаметр диафрагмы d
определяют возможность и точность
косвенной (расчетной) градуировки
расходомеров переменного перепада с
нормальными диафрагмами. Поэтому к этим
параметрам диафрагмы предъявляют весьма
высокие требования. Так, допустимое
отклонение оси отверстия диафрагмы от оси
трубы не должно превышать 0,015 D (D/d— 1),
где D — диаметр
трубопровода.
Диаметр отверстия
диафрагмы d не должен отличаться от
расчетного более чем на ± (0,001—0,05) % при т
< 0,45 и на ±(0,005—0,05) % при т > 0,45.
Этим обеспечивается геометрическое
подобие диафрагм.
Закругление,
смятие или затупление входной кромки
диафрагмы не допустимы, что обеспечивает
идентичность характера течения измеряемых
сред через однотипные
диафрагмы.
Давления у плоской
диафрагмы отбирают с помощью отдельных
сверлений. Для усреднения давлений
просверливают несколько отверстий,
равномерно распределенных по окружности
трубы в плоскостях отбора давлений.
Выходящие из отверстий трубки объединяются
двумя сборными коллекторами, от которых
давления передаются к
дифмано-метру.
Давления у камерных
диафрагм отбирают из камер, соединенных с
трубой кольцевыми щелями.

Преимуществом камерных
диафрагм является отоор действительных
средних давлений и в связи с этим несколько
менее жесткие требования к длине
прямолинейных участков^ трубопровода до и
после диафрагмы; недостатком —
необходимость специальных уплотнительных
устройств для герметизации
камер.
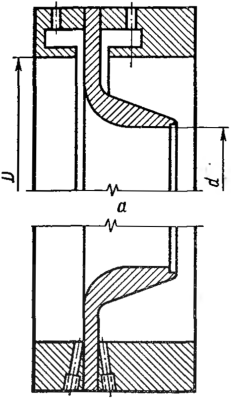
Нормальное сопло.
Нормальное сопло (рис. 59) выполняют в виде
насадка, имеющего входную сходящуюся часть,
образованную дугами окружностей с
радиусами г и г2,
равными 0,2d и d/З и
цилиндрическую часть диаметром d и
длиной 0,3с?.
Выходная кромка сопла, как и
у диафрагмы, должна быть острой, без
закруглений и заусенцев. Она предохранена
на выходе нишей.
<Г
Рис.
59. Нормальное сопло
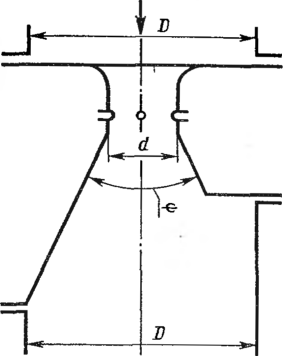
Рис.
60. Нормальная труба Вентури
Давления
также можно отбирать или при помощи камер и
кольцевых щелей (рис. 59, а) или через
отдельные отверстия (рис. 59,
б).
Нормальная труба (сопло)
Вентури. Существуют нормализованные
расходомерные трубы Вентури четырех
конструктивных разновидностей: трубы
Вентури с сопловым и коническим входами, с
длинным и коротким диффузорами.
На рис. 60
изображена труба Вентури с сопловым входом
(сопло Вентури) с длинным (снизу) и коротким
(сверху) диффузорами.
Входная часть
трубы до места отбора минусового (меньшего)
давления имеет тот же профиль, что и
нормальное сопло. Длина цилиндрической
части составляет обычно (0,5—0,7) d Угол
входного конуса диффузора должен быть
менее 30 .
Плюсовое (большее) давление
отбирают как с помощью кольцевой камеры,
так и с помощью отдельных сверлений;
минусовое — с помощью отдельных
сверлений.
Наличие стандартных
сужающих устройств трех типов объясняется
относительными эксплуатационными
преимуществами и недостатками каждого из
них. Так, диафрагмы технологически просты и
в области т < 0,3 имеют меньшие
предельные числа Рейнольдса (Re^), чем сопла и
трубы Вентури. Кроме того, коэффициенты
расхода диафрагм менее подвержены влиянию
искажения профиля скоростей и пульсаций
потока. В то же время потери давления в
соплах и трубах Вентури (особенно в
последних) значительно меньше, чем у
диафрагм. Кроме того, точность измерения
расхода газов и пара с помощью сопел в
области диаметров трубопроводов, меньших 300
мм, выше, чем при использовании диафрагм (в
связи с большим постоянством коэффициента
сжимаемости е при применении сопел).
Надежность сопел и труб Вентури, связанная
с изменениями коэффициента расхода а
при износе или загрязнении входного
профиля сужающего устройства, значительно
выше, чем у
диафрагм.
Метрологические
характеристики и область применения
расходомеров переменного перепада
давления. Измерения расхода по переменному
перепаду давления, создаваемому сужающими
устройствами, относятся к
косвенным.
Рабочей формулой
измерений расходомеров данного типа в
самом общем виде является
![]()
(7.9)
где
к — числовой коэффициент; —
исходный коэффициент расхода, значения
которого для нормализованных сужающих
устройств приводятся в соответствующих
таблицах (например, в таблицах РД 50—213—80);
*ш — поправочный множитель на
шероховатость трубопровода; к$ —
поправочный множитель на остроту кромки
у диафрагм; к^е — поправочный
множитель на вязкость измеряемой среды,
который вводится в случае, если число
Рейнольдса в трубопроводе несколько меньше
предельного числа Рейнольдса для данного
типа и относительной площади сужающего
устройства; kt — поправочный
множитель на расширение сужающего
устройства.
На основании формулы (7.9)
по закону сложения средних квадратических
погрешностей относительная средняя
квадратическая погрешность измерения
расхода Oq при соблюдении условий
нормальной эксплуатации (при
осесимметричном потоке с нормальной эпюрой
скоростей и при отсутствии существенных
пульс^ционных и вращательных составляющих
скоростей)
oQ =
![]()
Средняя
квадратическая погрешность табличного
значения исходного коэффициента расхода
(экспериментальная погрешность при его
определении) зависит от относительной
площади сужающего устройства. Значения
этой погрешности для различных типов
сужающих устройств колеблются в пределах
от 0,2 до 0,7 %. я
Значения средних
квадратических погрешностей о^щ)ако, okRe соответствующих
поправочных множителей (погрешности их
экспериментальной оценки) зависят от типа
сужающего устройства, его относительной
площади, диаметра трубопровода, чисел
Рейнольдса и колеблятся от 0 (при наиболее
благоприятных условиях) до 1,5
%.
Напомним, что предельные значения
погрешностей определения коэффициента
сжатия е составляют 4(1—5)% для диафрагм и 2(1
— S’) % для сопел и труб
Вентури.
Как правило, закон
распределения действительных значений
погрешностей определения е в пределах
указанных допусков для однотипных сужающих
устройств неизвестен и в этом случае,
приняв его равновероятным, найдем
ое = 2,3(1—S) % для диафрагм и
а’е = 1,2(1—S) % для сопел и труб
Вентури.
Следовательно,
максимальные значения средней
квадратической погрешности определения е
(при S = 0) соответствуют °етах = 2,3 %
для диафрагм, Оетах = 1,2 % для сопел и
труб Вентури, а минимальные (при
S
= 0,75) &emin= 0,58 % и
0e‘min = 0,3 %
соответственно.
Далее, является
средней квадратической погрешностью
определения диаметра отверстия сужающего
устройства.
В соответствии с
принятыми нормами максимальная
допускаемая погрешность измерения
диаметра сужающего устройства равна ±0,1
% от d.
Тогда, приняв, как и в
предыдущем случае, равновероятное
распределение погрешностей в пределах
допуска, получим о а — 0,06
%.
Средняя квадратическая
погрешность определения коэффициента
расширения сужающего устройства
ак обычно мала по сравнению с
другими составляющими (даже при Т =
723 К ofc(– 0,02 %), поэтому, как
правило, ею можно пренебречь. Среднюю
квадратическую погрешность измерения
перепада давления определяют по
формуле
п — 1
(Ар)тПЯУ
R
Одп–—zz,
°кл»
V 3
(Др)ср
где (Ар)ср —
среднее расчетное значение перепада
давления, обычно принимаемое равным 4/9
(Др)тах; — максимальная
приведенная по
грешность
дифманометра, определяемая его классом
точности.
Формула также получена для
условий равновероятного распределения
погрешностей в пределах допуска для
однотипной совокупности
дифманометров.
Для обычных
эксплуатационных дифманометров при
соблюдении требований к их установке и
обслуживанию 5
кл 1*0 %
и для
диф
манометров со
вторичными приборами 5^ = 2,0—2,5 %.
Следовательно, Одр колеблется в
пределах от 1,3 до 3,2 %.
Средняя
квадратическая погрешность
ар характеризуется
погрешностью расчетного значения
плотности, взятого из соответствующих
справочных данных, изменением параметров,
влияющих на плотность измеряемой среды,
если отсутствуют корректирующие
устройства, и неточностью корректировочных
поправок, если имеются корректирующие
устройства. Для нормальных условий
применения сужающих устройств Ор = 0,1—1,0 %.
Нижнее значение (0,1 %) соответствует
измерению чистых однофазных жидкостей,
верхнее (1,0 %) — измерению расхода газов
при незначительных колебаниях температуры
и давления. При наличии устройств
автоматической коррекции показаний
дифманометров данная погрешность также
будет лежать в пределах указанных
граничных значений (несколько уменьшится
лишь верхняя граница).

Определим теперь возможные
пределы изменения суммарной средней
квадратической погрешности измерения
расхода с помощью расходомеров переменного
перепада давления.
В лучшем случае —
при измерении расхода жидкостей (е = 1) и при
отсутствии необходимости введения
поправок на вязкость, шероховатость и
острота кромки
Oq = у/0,252 4
• 0,Об2 1/4 • 1,302 1/4 • 0,102 ‘ =
0,75 %.
В наиболее неблагоприятных
случаях (с учетом наибольших погрешностей
всех поправочных коэффициентов) средняя
квадратическая погрешность измерения
расхода может достигать 3,0—4 %.
Таким
образом, максимальная погрешность
измерения расхода (при доверительной
вероятности 0,95) с помощью расходомеров
переменного перепада давления при
нормальных условиях эксплуатации
колеблется в пределах от 1,5 до 8%.
– Указанные пределы
максимальных погрешностей измерений
характерны для косвенных (расчетных)
методов градуировки и поверки расходомеров
с нормализованными типами сужающих
устройств. При индивидуальной аттестации
расходомеров совместно с подводящими
участками трубопроводов и применении
дифманометров повышенной точности
основная погрешность этих расходомеров
может быть снижена доО,5—1%.
Для
нормальной работы сужающих устройств
необходимы достаточно длинные прямые
участки трубопровода, так как любые местные
сопротивления (колена, угольники,
конические встаЕки, вентили, задвижки и т.
п.), вызывая искажение эпюры скоростей по
сечению потока, его закручивание и
дополнительные пульсации, приводят к
отклонению действительных значений
коэффициентов расхода от табличных
(исходных)
и, как следствие, к
появлению дополнительных неконтролируемых
в процессе измерений
погрешностей.
Наименьшие
необходимые длины прямых участков h
перед (по ходу потока) сужающим устройством
при отборе давлений через кольцевые камеры
приведены на рис. 61 и 62. Если же давления
отбирают через отдельные отверстия, то
длина прямых участков должна быть
увеличена вдвое по сравнению с длинами,
указанными на этих рисунках.
Для
местных сопротивлений, создающих винтовое
движение потока, необходимая длина прямого
участка может быть уменьшена за счет
установки в трубопроводе перед сужающим
устройством (на расстоянии не
¦ f
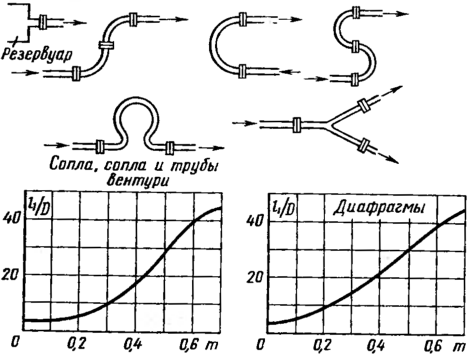
Рис.
61. Наименьшие допустимые длины прямых
участков трубопровода от местных
сопротивлений указанных видов до сужающего
устройства
Г”
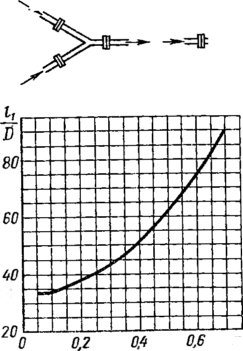
Рис. 62. Наименьшие допустимые
длины прямых участков трубопровода от
местных сопротивлений, создающих
винтообразное движение потока, до
сужающего устройства
менее
2D от него) специальных
струевыпрямителей, представляющих собой
либо мелкоячеистые сетки, либо набор
трубок, перекрывающих все сечения
трубопровода. При этом следует иметь в виду,
что струенаправляющие аппараты вызывают
дополнительные (и немалые) потери напора в
трубопроводе и требуют тщательного ухода в
связи с возможностью засорения и
износа.
Минимально допустимая длина
прямого участка /2 за сужающим
устройством зависит от его относительной
площади и равна 40 для т = 0,05 и
8D для т =
0,7.
Существующие нормализованные
сужающие устройства с унифицированными
табличными значениями исходных
коэффициентов расхода применимы лишь для
диаметров трубопровода больших 50 мм.
Расходомеры переменного перепада на
меньшие диаметры требуют индивидуальной
градуировки, и в этом случае пропадает
возможность их косвенной расчетной
аттестации по унифицированным табличным
данным. Кроме того, существенно возрастают
погрешности, связанные с шероховатостью
трубопровода, так как уменьшение диаметра
ведет к увеличению относительной
шероховатости. Поэтому расходомеры следует
градуировать комплектно с
эксплуатационными участками
трубопровода.
Унифицированные
табличные значения а„ и формулы для
расчета е пригодны при измерении расхода
однофазных (чистых) сред и
квазиста-ционарных потоков. И хотя в
практике сужающие устройства нередко
используют для измерения расхода
двухфазных сред (см. разд. 7.13) и измерения
пульсирующих расходов (см. разд. 7.14)
погрешности показаний расходомеров при
этом (без их индивидуальной градуировки
непосредственно на месте эксплуатации)
невозможно пронормировать и
оценить.
Измерение расходов с
помощью нормализованных сужающих
устройств в области малых чисел Рейнольдса
(при малых диаметрах трубопроводов, вязких
жидкостях, значительно нагретых газах и
других) практически невозможно из-за
непостоянства коэффициентов расхода (при Re
< Re^), а следовательно, и из-за
невозможности нормирования и оценки
реальной точности этих измерений. В
практике для измерений расхода при малых
числах Рейнольдса применяются некоторые
модифицированные типы сужающих устройств,
например, сопло с профилем „четверть
круга”, двойная диафрагма, сегментная
диафрагма, сопло с профилем „полукруг” и т.
п. Предельные числа Рейнольдса у этих
сужающих устройств получаются несколько
меньшими, чем у нормальных. Однако данные
устройства требуют индивидуальной
градуировки, как правило, непосредственно
на месте эксплуатации, их погрешности в
настоящее время не нормированы и применяют
их в основном в качестве
индикаторов.
Таким образом, область
нормального (с определенными и
нормированными погрешностями измерений)
применения расходомеров переменного
перепада давления ограничена измерением
стационарных расходов однофазных
жидкостей, сухого перегретого пара и сухих
газов на трубопроводах диаметром более 50 мм
с определенной длиной прямого участка, при
значительных числах Рейнольдса (Re > Re^,)
и в тех случаях, когда допустимо изменение
конфигурации потока.
Несмотря на эти
ограничения и относительно малую точность,
расходомеры переменного перепада получили
преимущественное распространение в
отечественной расходоизмерительной
практике. По-существу, они являются
единственным типом стандартизованных
расходоизмерительных устройств.
Они не требуют индивидуальной
градуировки и аттестации, обладают
унифицированными и взаимозаменяемыми
элементами, применимы при значительных
давлениях и температуре измеряемых сред. В
случае необходимости изменения предела
измерения в расходомере достаточно сменить
сужающее устройство (изменить
относительную площадь т), наиболее же
сложная и дорогостоящая часть прибора —
дифманометр — остается неизменной. Для
этого следует лишь изменить предел
измерения дифманометра или сменить его
шкалу.
Простота и надежность
сужающих устройств, определяемая при
правильной эксплуатации достаточно
медленными процессами износа, коррозии и
„зарастания” их входного профиля, также
способствовали широкому распространению
расходомеров переменного
перепада.
И наконец, метрологические
возможности (возможности повышения
точности) расходомеров этого типа на
сегодняшний день далеко не исчерпаны. Как
показали проведенные в последние годы
исследования, установка перед сужающими
устройствами специально спрофилированных
насадков (конфузоров и диффузоров),
обеспечивающих равномерное (прямоугольное)
распределение скоростей по сечению потока,
правильно „спланированный” набор
взаимокомпенсирующих возмущающих факторов
(например, отсутствие необходимой длины
прямого участка может частично
компенсироваться „закруткой” потока и т.
п.) в некоторых случаях могут существенно
повысить точность расходомеров
переменного перепада
давления.
Установка и обслуживание
расходомеров переменного перепада
давления. Существенное влияние на
правильность работы данных расходомеров
оказывает взаимное расположение сужающего
устройства и дифманометра, а также монтаж
соединительных (импульсных) линий. Поэтому
для нормальной работы расходомеров при их
монтаже необходимо выполнить ряд общих и
частных (для различных случаев измерений)
требований.
Так, импульсные линии к
сужающему устройству при измерении расхода
жидкостей в горизонтальном трубопроводе
присоединяют в нижней части поперечного
сечения трубопровода (ниже его
горизонтальной оси); при измерении расхода
пара — на горизонтальном диаметре
поперечного сечения трубопровода; при
измерении расхода газа — в верхней части
сечения трубопровода (выше его
горизонтальной оси).
Дифманометр
устанавливают по возможности ближе к
сужающему устройству. Длина соединительных
трубок при этом для достаточного
сглаживания пульсаций давления должна быть
не менее 3 м. Диаметр трубок выбирают из
условий минимального динамического
запаздывания показаний дифманометра,
обычно он раиен 10—12 мм. Соединительные
трубки монтируют или вертикально, или с
уклоном 1:20 до 1:10. Монтаж соединительных
трубок должен обеспечить возможность их
периодической очистки, для чего используют
фланцевые или ниппельные
соединения.
При измерении расхода
жидкости или пара дифманометр
целесообразнее устанавливать ниже
сужающего устройства, чтобы предотвратить
попадание в него пузырьков воздуха.
Если же по каким-либо причинам дифманометр
монтируют выше сужающего устройства, то в
соединительных линиях устанавливают г
азосборники с кранами для выпуска воздуха.
В соединительных линиях (в наиболее
низко расположенных точках) устанавливают
также сосуды с кранами для слива
отстоявшейся грязи и взвешенных
частиц.
При измерении расхода пара
необходимо обеспечить одинаковый уровень
конденсата в соединительных трубках. Для
этого вблизи сужающего устройства
устанавливают уравнительные сосуды на
такой высоте, чтобы конденсат мог
накапливаться в них лишь до определенного
уровня, а превысив его, стекал бы обратно в
трубопровод. Тем самым устраняют ошибку в
показаниях дифманометра за счет разностей
уровней конденсата в соединительных
линиях.
При измерении расхода газа
дифманометр следует располагать выше
сужающего устройства для того, чтобы
содержащаяся в газе влага не попадала в
дифманометр. Если же его можно монтировать
только ниже сужающего устройства, то в
наиболее низко расположенных точках
соединительных линий устанавливают
дренажные устройства.
Качественное
техническое и метрологическое состояние
расходомеров обеспечивается комплексом
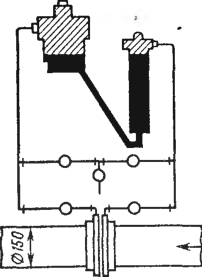
мероприятий по их обслужи-Рис. 63. Схема к
контроль- Ванию, регламентируемым
соответствующими ному вопросу
инструкциями и
правилами.
Контрольный вопрос
№ 11
Проектировщиками был разработан
оптимальный процесс измерения расхода на
технологической линии.
Глядя на рис. 63,
ответьте, какое сужающее устройство (сопло
или диафрагму) было решено установить в
трубопроводе?
Если Вы решите, что сопло,
загляните на с. 154, если – диафрагму, то см. с.
155.
7.2. Расходомеры постоянного
перепада давления
Общая
характеристика расходомеров постоянного
перепада давления. Расходомеры данного
типа довольно широко применяются в
системах автоматического контроля и
регулирования в химическои и топливной
промышленности из-за конструктивной
простоты; высокой чувствительности и
вследствие этого возможности применения
для измерения весьма малых расходов;
возможности применения для измерения
расхода агрессивных жидкостей и газов;
простоты автоматизации измерений;
постоянства относительной погрешности и
вследствие этого значительного диапазона
измерения Gmax/Gmin = Ю:1 (для
расходомеров переменного перепада он
составляет 3:1); незначительных потерь
давления.
Однако эти приборы имеют и
существенные недостатки, препятствующие их
массовому применению: отсутствие научных
принципов взаимозаменяемости и косвенной
расчетной градуировки; необходимость
индивидуальной градуировки на реальных
измеряемых средах и существенные потери
точности при измерении других сред,
отличных от тех, на которых осуществлялась
градуировка; непригодность для измерения
больших расходов.
В настоящее время
разработано и предложено несколько
способов пересчета результатов опытных
градуировок расходомеров постоянного
перепада давления, проводимых на воде или
на воздухе, на реальные измеряемые среды.
Однако ни один из них не является
универсальным и достаточно достоверным.
Подробнее некоторые из этих способов будут
рассмотрены ниже.
Существуют
расходомеры постоянного перепада давления
трех конструктивных разновидностей:
ротаметры, поршневые и поплавковые
расходомеры. Принцип действия всех этих
приборов основан на силовом взаимодействии
потока и помещенного в него
тела.
Ротаметры. Основными
элементами ротаметра (рис. 64), принципиально
необходимыми для его работы, являются
расширяющаяся кверху (по ходу
вертикального потока) коническая трубка
1 и заключенный в нее поплавок 2. Для
визуального отсчета показаний применяют
стеклянную трубку, непосредственно на
которую нанесены деления шкалы
прибора.
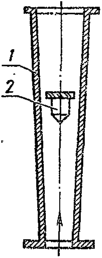
Поплавок состоит из нижней
конической и средней цилиндрической части,
заканчивающейся бортиком с косыми
канавками. Назначение канавок — обеспечить
устойчивое вращение поплавка при течении
измеряемой среды, что необходимо для его
центрирования относительно оси
трубки.
При использовании
ротаметров в системах автоматического
регулирования или контроля необходимы
допол-Рис. 64. Ро- нительные устройства,
преобразующие ход поплавка в про-таметр
порциональный механический, электрический
или пневматический сигналы.
Принцип
действия ротаметров состоит в следующем.
Гидродинамическое давление потока
измеряемой среды воздействует на поплавок
и вызывает его вертикальное перемещение.
При этом (в связи с конусностью трубки)
изменяется площадь проходного сечения
прибора, образованного диаметром буртика
поплавка и внутренней стенкой
трубки.
Это изменение площади
происходит таким образом, что перепад
давления по обе стороны поплавка остается
практически постоянным (отсюда и название
расходомеров).
Поплавок будет
подниматься до тех пор, пока его вес и вес
связанных с ним элементов не уравновесит
уменьшающееся (вследствие уменьшения
скорости из-за увеличения проходного
сечения) по мере подъема поплавка
динамическое давление
потока.
Следовательно, условие
равновесия поплавка будет иметь
вид
Гп(рп-р)*г = спр^-/п,
(7.11)
где Fn —
объем поплавка; рп —
плотность материала поплавка; р
— плот
ность измеряемой
среды; сп — коэффициент
сопротивления поплавка, зависящий в общем
случае от числа Рейнольдса, шероховатости,
формы, геометрических.размеров и высоты
подъема поплавка; /п — наибольшее
поперечное (миделево) сечение поплавка;
v — средняя скорость потока
в кольцевом сечении, ограниченном с
внутренней стороны/п и с внешней
площадью сечения трубки FT,
соответствующей подъему
поплавка.
Так как расход для
рассматриваемого случая Q = v (FT —
/п), иэ уравнения (7.Ц)
получим
в = «p(FT
-/п) у/ —— (7-12)
где
Ир = 1/V сп — коэффициент
расхода ротаметров, а в
общем случае
коэффициент
расхода расходомеров постоянного перепада
давления.
Уравнение (7.12) является
общим уравнением измерений для всех
расходомеров постоянного
перепада.
Как следует из
вышеизложенного, коэффициент расхода
«р зависит от большого числа факторов
и непостоянен по шкале прибора. Эти
обстоятельства и приводят к ряду
теоретических и практических трудностей
при пересчетах результатов градуировок
ротаметров на условия, отличные от условий
градуировки.
4Для конической
трубки площадь FT задается
соотношением
Fr = f-{D0
2Htg-f-f = -*-(Я02 4HD0 tg-f
4/^tg2-|-),(7.13)
где D0— внутренний диаметр трубки
на нулевом делении; Н — высота подъема
поплавка относительно нулевого деления; 5 —
центральный угол конической
трубки.
Если центральный угол S мал
(обычно 5 = 35′), то квадратическим членом в
правой части формулы (7.13) г^ожно пренебречь.
В этом случае уравнение измерений для
ротаметров (связь между ходом поплавка и
расходом) на основе формул (7.12) и (7.13) будет
иметь вид
Как видно из уравнения (7.14),
при малых 5 между ходом поплавка и расходом
существует приближенная линейная
пропорциональность, что также является
достоинством расходомеров постоянного
перепада давления.
Основы пересчета
градуировок ротаметров. Наиболее общим
подходом к пересчету градуировок
ротаметров является установление
некоторых универсальных зависимостей,
определяющих Ор и ход поплавка для
геометрически подобных ротаметров со
стандартизованными формой и размерами их
элементов — поплавка и трубки. При высоком
уровне стандартизации, обеспечивающем
полное геометрическое подобие и
взаимозаменяемость элементов, и
достаточной достоверности полученных
зависимостей их можно было бы использовать
для косвенной (расчетной) градуировки
ротаметров (аналогично расчету сужающих
устройств по стандартизованным значениям
их коэффициентов расхода). При отсутствии
обоснованных норм, обеспечивающих точное
технологическое копирование элементов
ротаметров, каждый ротаметр градуируют
индивидуально. Причем, из-за отсутствия
специальных установок градуировку, как
правило, проводят на типовых контрольных
веществах (при измерении расхода жидкостей
— на воде, при измерении расхода газов на
воздухе). Поэтому применение ротаметров как
приборов с нормированной точностью для
измерения расхода реальных сред, свойства
которых отличны от свойств типовых
контрольных веществ, требует создания
достоверных способов пересчета
градуировочных данных.
Рассмотрим
один из наиболее общих способов пересчета,
разработанный во ВНИИМС под руководством
А.И. Петрова.
В процессе
теоретических и экспериментальных
исследований ротаметров было установлено,
что ход поплавка Д выраженный в долях
диаметра поплавка d, зависит от двух
безразмерных величин: числа Рейнольдса и
величины v2p/G, где v —
кинематический коэффициент вязкости
измеряемой среды; р — ее плотность и G —
кажущийся (с учетом выталкивающей силы) вес
поплавка. Между этими величинами
существует зависимость
вида
JL =fcRe”* (-^f)”s,
(7.15)
а
о
где коэффициент к и
показатели степени и1#п2 —
постоянные величины для геометрически
подобных ротаметров с одинаковой формой
поплавка и трубки.
Эти коэффициенты
для каждого типа ротаметра могут быть
экспериментально определены. В этом случае
при помощи специальных таблиц или
градуировочных кривых показания ротаметра
Н на одной измеряемой среде могут быть
пересчитаны на любую другую измеряемую
среду (с другой вязкостью и плотностью).
Естественно, это требует строгой
взаимозаменяемости и геометрического
подобия трубок и поплавков ротаметров, а
также .большой экспериментальной работы по
определению опытных коэффициентов. Такие
работы в настоящее время проводятся в
метрологических институтах Госстандарта
СССР.
Кроме того, в ряде
отечественных и зарубежных расходомерных
центрах ведутся экспериментальные
исследования по нахождению такой формы
поплавка (дисковой, тарельчатой,
катушечной), при которой влияние вязкости и
плотности измеряемой среды на показания
ротаметров можно свести к
минимуму.
Полученная на основе
теории подобия зависимость (7.15) позволяет
осуществить и достаточно простой
„технологический” метод градуировки
ротаметров ^.заключающийся в изменении веса
поплавка таким образом, чтобы значение
критерия v2p/G оставалось
постоянным, т. е. в случае необходимости
измерения расхода жидкости или газа,
вязкость и плотность которых отличаются от
вязкости и плотности градуировочной среды,
необходимо и достаточно лишь изготовить
новый поплавок весом G2—vlv ¦
Р2/Р1Gi, где Gt — вес
поплавка ротаметра, градуированного на
среде с вязкостью vx и плотностью
pt.
Если форма и размеры нового
поплавка полностью соответствуют старому,
то новые значения шкалы прибора Q2
(соответствующие тому же ходу поплавка//)
подсчитывают, исходя из равенства чисел
Рейнольдса по формуле Q2
—Qi • v-i/vi ¦
Этот
метод очень простой, так как не требует
построения экспериментальных пересчетных
таблиц и графиков и пригоден для ротаметров
любых размеров и любой формы
поплавка.
К недостаткам метода можно
отнести сложность точного
технологического копирования поплавков и
невозможность существенного варьирования
их веса в случае, когда вязкости v2
и vt значительно отличаются друг
от друга.
Одним из перспективных
путей расширения областей применения
ротаметров для измерений расхода различных
сред с гарантированной точностью является
создание условий автомодельности их
коэффициентов расхода «р, т. е. условий, при
которых Ир принимает постоянное значение и
перестает зависеть от изменений вязкости и
плотности измеряемых сред.
Как
показали исследования, автомодельность Ир
для ротаметров с поплавками, имеющими в
верхней части тонкий цилиндрический диск,
наступает при числах Рейнольдса,
характерных для течения среды в зазоре
между трубкой и поплавком, больших
500.
Таким образом, если и при
градуировке, и при работе ротаметра на
реальной измеряемой среде обеспечивается
соотношение
вт1п№т~ *0 __
Cmin
где Gmin — нижний предел
измерений ротаметра; Dm — диаметр
трубки на отметке шкалы ротаметра,
соответствующей Omin. то на основании
выражения (7.14) реальная функция
преобразования ротаметра (градуировочная
характеристика на реальной измеряемой
среде) будет отличаться от его исходной
градуировочной характеристики Н = AQ — В
постоянным сомножителем
1 – -5- у/ Р^Рг
– 1 У Рп/Р, – 1 ‘
Ъ
—–— ¦ –—– .
1 –
‘ГPnlPi sTpJp^T”
D
Это
значит, что каждое новое (пересчитанное)
показание ротаметра Яр1>
соответствующее расходу ?2,-, будет
Яр,- = bHTi гдеЯп-,—
показание ротаметра, соответствующее
расходу Q* в условиях
градуировки.
.Сам метод прост, но для
его осуществления необходим выбор таких
конструктивных параметров поплавка,
которые в достаточно широком диапазоне
изменения вязкости обеспечат соотношение
(7.16).
Рассмотренные примеры
показывают, что и те, кто сейчас еще только
осваивает по этому учебнику азы
расходометрии, будут иметь широкие
возможности для творческих поисков
повышения точности даже таких, казалось бы,
простейших и хорошо изученных средств
измерения расхода, как
ротаметры.
Поршневые и поплавковые
расходомеры. Поршневые расходомеры
применяются для измерения расхода воды,
нефтепродуктов, вязких и агрессивных
жидкостей. Устройство поршневого
расходомера показано на рис. 65. В корпусе
прибора 1 запрессована цилиндрическая
бронзовая втулка 2, имеющая круглое
входное отверстие и прямоугольное
выходное. Внутри втулки под действием
динамического давления потока измеряемой
среды перемещается поршень 3 с грузами
8, открывая или перекрывая выходное
отверстие. Положение поршня, являющееся
мерой расхода вещества, передается с
помощью штока 7 и фиксируется индукционной
системой 4, 5, 6.
Конструктивно
корпус, втулка и поршень выполняются таким
образом, что в крайнем нижнем положении
поршня выходное отверстие остается
полностью открытым, а входное полностью
закрытым.
Предел измерений прибора
регулируется изменением ширины выходного
отверстия.
Если у измеряемого
вещества высокая температура, крышка
прибора снабжается ребристым охладителем,
если низкая температура и большая вязкость,
то крышка обогревается паром или горячей
водой.
Поршневой расходомер следует
устанавливать на горизонтальном участке
трубопровода длиной не менее 10Z? до прибора
и не менее 8D после прибора. В
случае измерения расхода загрязненных
жидкостей перед прибором монтируют
фильтр.
Принцип действия
поплавковых расходомеров (рис. 66)
аналогичен принципу действия ротаметров и
поршневых расходомеров. В
данном
случае динамическое давление
потока измеряемой среды воздействует на
поплавок, занимающий в зависимости от
величины расхода определенное положение
относительно седла, находящегося в корпусе
вентильного типа.
Основные
недостатки ротаметров (необходимость
индивидуальной градуировки и существенное
влияние свойств измеряемых сред на
точность измерений) сохраняются и у этих
расходомеров.
Метрологические
характеристики и область применения
расходомеров постоянного перепада
давления. В настоящее время нормируются
погрешности лишь тех расходомеров
постоянного перепада, которые были
индивидуально градуированы на реальной
измеряемой среде. В этом случае при
постоянных (и не отличающихся от условий
градуировки) уело-
Рис. 66. Поплавковый
расходомер:
1 — поплавок; 2 —
измерительное сопло;
3 — шток; 4 —
диск, предохраняющий механизм от нагрева- 5 –
втулка с уплотнительной набивкой; 6 —
диафрагма для записи показаний; 7 —
счетный указатель; 8 —
уравновешивающий груз; 9 — поршень для
обеспечения плавного движения
поплавка
виях измерений погрешность
приборов будет определяться погрешностями
их градуировки (бгр), отсчета показаний
(Ън) и нелинейности шкалы
(6нел).
Существующие
установки для градуировки промышленных
ротаметров позволяют градуировать их с
погрешностью, не превосходящей 0,2—
0,3 %. Следовательно, среднее квадратическое
значение погрешности градуировки (при
равновероятном ее распределении в пределах
допусков) может оцениваться величиной ст^,
— агр//”3 = 0,18 %.
Среднее
квадратическое значение погрешности
бн определяется ошибкой отсчета,
равной половине целения шкалы (при
визуальном отсчете, например, у стеклянных
ротаметров), и у применяемых приборов
данного типа достигает 1,5-2,0 % (при Q ?=
¦
Погрешность
вследствие нелинейности шкалы бнел
связана, в основном, с непостоянством
коэффициента расхода ctp при изменении
положения поплавка и связанных с этим
изменений структуры потока. Обычно среднее
квадратическое значение этой погрешности
5нет по аналогии с сужающими
устройствами принимают равным 0,5—0,6
%.
Вы правы. Как следует из схемы
соединительных линий в случае, показанном
на рис. 38, измеряется расход газа. Поэтому ¦
при диаметре трубопровода, меньшем 300 мм, по
причинам, указанным в разд.
7.1,целесообразнее применять нормальное
сопло.
Если Вы рассуждали аналогичным
образом, то в материале учебника,
относящемся в расходомерам переменного
перепада давления, Вы разобрались
достаточно хорошо.
Просуммировав все
составляющие, получим наибольшую по шкале
(при Q = 0,lQmax) относительную среднюю
квадратическую погрешность расходомеров
постоянного перепада давления
6^, Ьд =1,6
—2,2%.
Максимальная (с
доверительной вероятностью Р = 0,9973)
приведенная к верхнему пределу измерений
расхода погрешность данного типа
расходомеров составит 8щ, = 3/10 •
ар — 0,5 — 0,7 %.
При
колебаниях плотности измеряемой среды,
характеризуемых средним квадратическим
значением ар, к рассмотренным выше
составляющим добавляется дополнительная
погрешность вследствие колебаний
плотности среды, равная на основании
формулы (7.14)
* _
г _ . V3”1
рп
БР= ±
—°р-
2 рп-р
Таким
образом, при индивидуальной градуировке,
проведенной на реальной измеряемой среде,
расходомеры постоянного перепада давления
могут применяться как приборы с
нормированной точностью для измерения
расхода жидкостей, газов или пара. При этом,
в случае измерения однофазных чистых-сред с
незначительными изменениями их вязкости и
плотности точность измерения расхода
данными приборами выше, чем точность
измерения расходомерами переменного
перепада давления. Нормальные (не влияющие
на точность) условия их эксплуатации
определяются лишь наличием достаточно
длинных вертикальных (для ротаметров) или
горизонтальных (для поршневых и
поплавковых расходомеров) участков
трубопровода.
Без индивидуальной
градуировки или при градуировке на средах,
отличных от измеряемой, расходомеры
постоянного перепада в настоящее время (до
разработки и внедрения правил пересчета
результатов градуировок) можно применять
лишь как устройства индикаторного типа,
качественно характеризующие изменения
расхода (больше — меньше, есть расход — нет
расхода). Устройства такого типа используют
в системах автоматического регулирования и
контроля за ходом различных
технологических процессов в химической,
газовой, топливной промышленности и др.
Простота, хорошие динамические
характеристики (постоянная времени 0,5—1 с),
устойчивость к агрессивным средам — эти
свойства ротаметров способствовали их
наибольшему распространению в упомянутых
системах.
В настоящее время серийно
выпускают ротаметры показывающие со
стеклянной трубкой типа PC, ротаметры с
электрической дистанционной передачей
типа РЭ и ротаметры с пневматической
дистанционной передачей типа
РП.
л»
Контрольный вопрос №
12
Определите знак дополнительной
ошибки, вызванной термическим расширением
поплавка ротаметра.
Если Вы решите, что
ошибка положительна, загляните на с. 157; если
отрицательна, обратитесь к с. 159.
К
контрольному вопросу № 11
Вы неправильно
ответили на вопрос, поэтому Вам необходимо
заново повторить разд. 7.1.
7.3. Турбинные
расходомеры
Общие характеристики.
Турбинные (или как их часто называют
та-хометрические) расходомеры являются
наиболее точными приборами для измерения
расхода жидкостей. Приведенная погрешность
измерения расхода турборасходомерами
составляет значение порядка 0,5—1,0 %
(известны турборасходомеры с приведенной
погрешностью 0,1—0,2
%).
Приборы просты по конструкции,
имеют большую чувствительность и большие
пределы измерений (для одной модификации
10:1 и более), возможность измерения как
малых (от 5 • 10-9 м3/с), так и
достаточно больших (до 1 м3/с)
расходов жидкостей с широким диапазоном
фи-зико-химических свойств, малую
инерционность и вследствие этого
относительно малые динамические
погрешности при измерении средних и
мгновенных значений расходов. Их, в
основном, применяют там, где требования к
точности измерений превалируют, например, в
ракетной и авиационной технике.
К
недостаткам турбинных расходомеров
существующих модификаций, препятствующим
более широкому применению данных приборов,
можно отнести: необходимость
индивидуальной градуировки и вследствие
этого необходимость наличия
градуировочных установок высокой точности;
влияние изменения вязкости измеряемой
среды и гидродинамических параметров
потока на показания приборов; наличие
изнашивающихся опор, что резко сокращает
срок службы приборов (особенно при
измерении расхода абразивных сред), снижает
их точность в процессе эксплуатации и
приводит к необходимости их частых
переградуиро-вок (уточнения значений
меняющихся в процессе эксплуатации
градуировочных коэффициентов).
В
настоящее время отечественным
приборостроением разработаны и
осваиваются безопорные турбинные
расходомеры, турбинные расходомеры с
устройствами автоматической коррекции
показаний при изменении вязкости
измеряемой среды, у которых два последних
недостатка отсутствуют.
Принципдействия. Уравнение измерений. Для
осуществления процесса измерений
турбинный расходомер (рис. 67) должен
состоять, по крайней мере, из трех элементов
; турбинного первичного преобразователя
вторичного преобразователя 4
отсчетной системы (регистратора) 1.
Турбинный преобразователь представляет
собой аксиальную или тенгенциальную
лопастную турбинку (на рис. 67 показана
аксиальная турбинка), опирающуюся на
керновые подпятники или подшипники
2.
Поток измеряемой среды,
воздействуя на наклонные лопасти турбинки,
сообщает ей вращательное движение с
угловой скоростью со, пропорциональной
расходу Q.
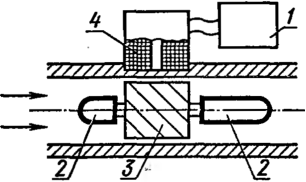
Рис.
67. Принципиальная схема турбинного
расходомера
Вторичный
преобразователь, изображенный на схеме,
представляет собой индукционную катушку.
При пересечении магнитного поля катушки
лопастями ферромагнитной турбинки в
катушке наводится пикообразный
пульсирующий ток. Частота пульсаций
наведенного тока пропорциональна угловой
скорости вращения турбинки, а
следовательно, и измеряемому расходу. В
качестве вторичных преобразователей
используются также индуктивные катушки, в
которых при вращении ферромагнитной
турбинки создается периодическое
изменение индуктивности, вызывающее
соответствующие изменения одного из
параметров текущего через нее тока.
Применяются также и фотоэлектрические
элементы.
Импульсы пульсирующего тока
регистрируются отсчетной системой. Общее
число импульсов, зарегистрированных этой
системой за время t, характеризует
суммарное количество вещества, протекающее
по трубопроводу за это время. Число
импульсов, зарегистрированных
(отсчитанных) системой за единицу бремени,
характеризует расход измеряемого
вещества.
Уравнение равномерного
вращения лопастной турбинки имеет
вид
Mm = ZMci,
(7.17)
где Мда — движущий
момент на роторе турбинки, сообщаемый ей
потоком измеряемой среды; 2 Mci
— сумма моментов сопротивления.
На
основе известного уравнения Эйлера (на
котором базируются все расчеты турбинных
двигателей) для осевого входа потока
движущий момент
М№ = ар Q2
— bp Q со, (7.18)
где а и
Ъ — коэффициенты, определяемые
конструктивными параметрами турбинного
датчика (радиусом лопастей R,
радиусом ступицы турбинки г, углом наклона
лопастей а) и зависящие от числа Рейнольдса
в области неавтомодельного
потока.
Если предположить, что на
турбинны датчик не действует никаких
моментов, препятствующих его вращению, т. е.
что 2 Ми = 0, то на основании формулы
(7.18) зависимость менру угловой скоростью
вращения датчика со и расходом Q
определялась бы
уравнением
o>=AQ,
(7.19)
где А =
а/Ь.
В действительности же на
турбинку действуют моменты сил
гидравлического трения жвдкости, момент
сил трения в опорах и ряд других. Действие
этих моментов будет характеризоваться так
называемой зоной нечувствительности
прибора, т. е. тем наименьшим расходом
(Q0), который необходим для того,
чтобы преодолеть моменты сопротивления и
сдвинуть турбинку с места или изменить ее
установившуюся скорость вращения.
С
учетом сказанного из формулы (7.19) получим
рабочее уравнение турбинных
расходомеров
gj =
A(Q-Q0).
(7.20)
Так как коэффициент
А и величина Q0 определяются в
процессе непосредственной градуировки, то
уравнение (7.20), решенное относительно Q,
называют иногда градуировочной
зависимостью турбинных
расходомеров.
Как следует из этого
уравнения, область постоянной линейной
зависимости угловой скорости вращения
турбинки от расхода определяется зоной
постоянства коэффициента А и величины
Q0, которые в общем случае кроме
конструктивных параметров прибора зависят
также от числа Рейнольдса, структуры потока
(его Искажений и „закрутки”), расхода и
вязкости измеряемой среды.
Значение
Q0 при правильном проектировании и
изготовлении турбинных датчиков (малый
коэффициент трения в опорах, отсутствие
перекосов, хорошая балансировка турбинки,
защищенность от осевых нагрузок) может быть
сведено к ничтожно малому, что и
обеспечивает высокую чувствительность и
большой диапазон измерений турбинных
расходомеров.
Метрологические
характеристики и область применения
турбинных расходомеров. Основными
составляющими погрешности турбинных
расходомеров при нормальных (ке
отличающихся от условий градуировки)
условиях их эксплуатации являются:
К
контрольному вопросу № 12
Вы правильно
ответили на вопрос.
Действительно,
увеличение диаметра поплавка при том же
расходе через ротаметр приводит к
увеличению силы, действующей на поплавок со
стороны потока, а следовательно, и к
большему его подъему относительно нулевого
деления шкалы.
погрешность
градуировки прибора на образцовой
расходомерной установке бгр, т. е.
погрешность определения градуировочных
значений
А и
е0;
погрешность счета (или
регистрации количества импульсов,
соответствующих угловой скорости вращения
турбинки бдг;
погрешность 6,
регистрации времени счета импульсов
t.
Погрешность = AN/Nmin,
где ДN — ошибка счета импульсов, обычно
равная ± 1 импульс, iYmin — суммарное
число импульсов, поданное на счетную
систему при минимальном расходе за время
t.
Увеличивая Nmia за счет
увеличения t, угла наклона лопастей
а, числа лопастей г турбинки или
заполняя импульсные паузы
высокочастотными модулированными
сигналами, можно свести погрешность
SN практически к любому сколь
угодно малому значению.
Погрешность
6, высокоточных электронных
чаетотомеров, применяемых для счета
импульсов, составляет в худшем случае (при
t = 1 с) 1(Г3-1(Г4
%.
Таким образом, погрешность измерения
расхода турбинными расходомерами при
нормальных условиях эксплуатации и в
случае применения высокоточных отсчетных
систем для регистрации N vit практически
целиком определяется погрешностями их
градуировок.
Основными
эксплуатационными факторами, существенно
влияющими на точность измерения расхода
турбинными расходомерами, являются:
изменение вязкости измеряемой среды;
закрутка потока и неравномерность
распределения скоростей, вызванные
наличием близко расположенных местных
сопротивлений и износ
опор.
Вследствие этого данные
приборы мало пригодны для измерения
расхода загрязненных или абразивных сред, а
также жидкостей, сильно меняющих свою
вязкость, в условиях эксплуатации
приборов.
Если не принять
соответствующих мер для частичной или
полной компенсации влияния указанных
факторов, то дополнительные погрешности,
например, вследствие изменения
кинематического коэффициента вязкости
измеряемой среды всего лишь на 10 % могут
достигать 3 % и более, а из-за близкой
установки 90-градусного колена трубопровода
—
2-5 %.
Для снижения влияния
вязкости применяют различного рода
устройства (сетки, спицы, конфузоры),
устанавливаемые перед турбинкой и
искусственно турбулизирующие
поток.
Влияние местных
сопротивлений, закручивающих поток, в
значительной мере устраняется, если перед
турбинным датчиком установлены
специальные направляющие или сопловые
аппараты. В этом случае для нормальной
работы, турбинных датчиков не требуется
столь длинных прямых участков
трубопровода, как для других типов
расходомеров.
Для измерения расхода
газов сравнительно редко применяют
турбинные расходомеры. Это объясняется тем,
что движущий момент на роторе турбинки в
газовых потоках вследствие их малой
плотности получается значительно меньшим,
чем в жидкостных, в результате чего
уменьшается чувствительность прибора и
диапазон измерений. Кроме того, большие
скорости газовых потоков ускоряют износ
опор.
Турбинные расходомеры
обладают достаточно хорошими
динамическими характеристиками
(постоянной времени 0,001 с), поэтому их
мож-
но применять для измерения
мгновенных значении расхода в пульсирующих
потоках.
Контрольный вопрос № 13
д
Две совершенно идентичные
турбинки установлены непосредственно друг
за другом.
Какая из турбинок будет
вращаться с большей угловой скоростью
вращения при одном и том же расходе —
первая (по ходу потока) или вторая?
Если
Вы решите, что первая — см. с. 168; если вторая
— см. с. 174.
К контрольному вопросу №
12
Вы не поняли физический принцип работы
расходомеров постоянного перепада
давления.
Повторите заново разд. 7.2 и
уясните себе, каким образом и за счет чего
поднимается поплавок ротаметра?
К
тахометрическим расходомерам, кроме
турбинных, относятся и шариковые
расходомеры, получившие достаточно широкое
распространение для измерения расхода
агрессивных сред и сред, содержащих
абразивные включения, т. е. там, где трудно
обеспечить надежную работу опор турбинных
датчиков. .
Подвижным элементом
шарикрвых расходомеров является шарик,
непрерывно движущийся в одной плоскости по
внутренней поверхности трубы под
воздействием предварительно закрученного
винтовым направляющим аппаратом потока
жидкости. От перемещения вдоль оси трубы
шарик удерживается ограничительным
кольцом. Неподвижные лопасти служат для
„выпрямления” потока на выходе из
преобразователя. Для преобразования
скорости вращения шарика в частоту
импульсов тока служит индукционное или
индуктивное устройство. Шар под действием
центробежной силы прижимается к внутренней
поверхности трубы, а под действием осевой
составляющей скорости потока — к
ограничительному кольцу. Поэтому шару
помимо сил вязкостного трения жидкости
приходится преодолевать силы трения о
поверхность трубы и ограничительного
кольца. Это вызывает отставание окружной
скорости шара vm от соответствующей
окружной скорости потока v. Это отставание
характеризуется скольжением SCK,
равным?ск = (v – vm)/v.
Откуда,vm = v(1 — SCK). Как
следует из этого соотношения,
пропорциональность между угловой
скоростью вращения шара и скоростью потока
измеряемой среды обеспечивается при
постоянстве скольжения SCK.,
которое зависит, в основном, от лобового
сопротивления шара. Следовательно,
шариковые расходомеры целесообразно
использовать там, где коэффициент лобового
сопротивления шара С остается (в
приемлемых пределах) постоянным, т. е. в
автомодельной для С по числу Рейнольдса
зоне, которая обычно принимается равной
103 < Re < 10s.
7.4. Электромагнитные
расходомеры
Принцип действия.
Уравнение измерении. В проводнике,
пересекающем силовые линии магнитного
поля, индуцируется ЭДС,
пропорцио
нальная скорости движения
проводника. При этом направление тока,
возникающего в проводнике, перпендикулярно
к направлению движения проводника и
направлению магнитного поля.
Это
известный закон электромагнитной индукции
— закон Фарадея.
Если заменить
проводник потоком проводящей жидкости,
текущей между полюсами магнита, и измерять
ЭДС, наведенную в жидкости по закону
Фарадея, можно получить принципиальную
схему электромагнитного расходомера (рис.
68), предложенную еще самим
Фарадеем.
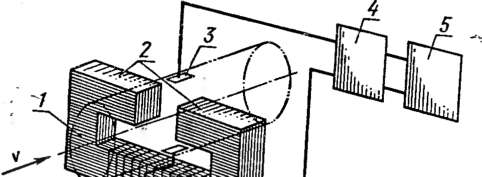
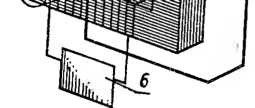
Рис. 68. Принципиальная схема
электромагнитного расходомера:
1 —
трубопровод; 2 — полюса магнита;
3
— электроды для съема ЭДС; 4 —
электронный усилитель; 5 — отсчетная
система; 6 — источник питания
магнита
Индуцируемую разность
потенциалов Е на электродах 3
определяют по уравнению электромагнитной
индукции
E=-KBDv с,
(7.21)
где В —
магнитная индукция в зазоре между полюсами
магнита; средняя скорость потока жидкости;
D — внутренний диаметр
трубопровода; К —
коэффициент, зависящий от вида магнитного
поля.
Для случая постоянного
магнитного шля К= 1. Если же
магнитное поле изменяется во времени t с
частотой f,ioK = sin
2irft.
Магнитное поле
создается источником питания 6 магнита (см.
рис. 68). ЭДС, снимаемую с электродов, при
помощи электронного усилителя 4,
преобразуют в усиленный электрический
сигнал, регистрируемый отсчетной системой
5.
Выражая в уравнении (7.21)
среднюю скорость потока через объемный
расход измеряемой среды, получим уравнение
измерений электромагнитных
расходомеров:
для случая
постоянного магнитного
поля
E=-A-^~Q:
(7.22)
пD
для случая
переменного магнитного поля
Таким
образом, электромагнитные расходомеры
могут быть выполнены как с постоянными, так
и с электромагнитными, питаемыми
переменным током частотой f. Эти
электромагнитные расходомеры имеют свои
достоинства и недостатки, определяющие
области их применения.
Метрологические
характеристики и область применения
электромагнитных расходомеров.
Погрешность данных приборов определяется в
основном погрешностями их градуировки
(определения постоянной величины С =
AKBfuD) и измерения разности
потенциалов Е. Однако
электрохимические процессы в потоке
жидкости, различные помехи и наводки,
непостоянство напряжения питания и другие,
не позволяют пока получить той
потенциально высокой точности измерений
расхода, которая вытекает из принципа
действия данного типа расходомеров. Так,
изготовляемые в СССР электромагнитные
расходомеры, несмотря на индивидуальную
градуировку, (на высокоточных
расходомерных стендах) и весьма
совершенные средства измерения Е
имеют класс точности 1,0—
2,5
%.
Существенным и основным недостатком
электромагнитных расходомеров с
постоянным электромагнитом,
ограничивающим их применение для измерения
слабопульсирующих потоков, является
поляризация измерительных электродов, при
которой изменяется сопротивление
преобразователя, а следовательно,
появляются существенные дополнительные
погрешности. Поляризацию уменьшают,
применяя электроды из специальных
материалов (угольные, каломадиевые) или
специальные покрытия для электродов
(платиновые, танталовые).
В расходомерах
с переменным магнитным полем явление
поляризации электродов отсутствует, однако
появляются другие эффекты, также
искажающие полезный сигнал.
Во-первых,
это трансформаторный эффект, когда на
витке, образуемом жидкостью, находящейся в
трубопроводе, электродами, соединительными
проводами и вторичными приборами наводится
трансформаторная ЭДС, источником которой
является первичная обмотка системы
возбуждения магнитного поля.
Трансформаторные помехи могут достигать
20—30 % полезного сигнала. Для их
компенсации в измерительную схему прибора
вводят специальные дополнительные
устройства.
Во-вторых, имеет место
емкостный эффект, возникающий из-за большой
разности потенциалов между системой
возбуждения магнитного поля и электродами
и паразитной емкости между ними
(соединительные провода и т. п.). Средством
борьбы с этим эффектом является тщательная
экранировка.
В-третьих, может иметь
место эффект влияния изменения частоты
питающего систему возбуждения магнитного
поля тока. Компенсируют этот эффект
установкой специальных стабилизирующих
устройств, что усложняет измерительные
схемы и уменьшает надежность
приборов.
Тем не менее электромагнитные
расходомеры широко применяют в
металлургической, биохимической и пищевой
промышленности, в строительстве и
руднообогатительном производстве, в
медицине, так как они малоинерционны по
сравнению с расходомерами других типов.
Расходо-
меры незаменимы в тех
процессах автоматического регулирования,
где запаздывание играет существенную роль,
или при измерений “быстро меняющихся
расходов. ;
Первичные
преобразователи электромагнитных
расходомеров не имеют частей, выступающих
внутрь трубопровода (электроды
устанавливаются заподлицо со стенкой
трубопровода), сужений или изменений
профиля. Благодаря этому гидравлические,
потери на приборе минимальны. Кроме Того,
преобразователь расходомера и
технологический трубопровод можно чистить
и стерилизовать без демонтажа. Поэтому зти
расходомеры используют в биохимической и
пищевой промышленности, где доминирующими
являются требования к стерильности
измерений среды. Отсутствие полых
углублений исключает застаивание и
коагулирование измеряемого
продукта.
На показания
электромагнитных расходомеров не влияют
взвешенные в жвдкоСти частицы и пузырьки
газа, осесимметричное (а в каналах
специальной формы любое) измерение профиля
распределения скоростей потока, а также
физико-химические свойства измеряемой
жидкости (вязкость, плотность, температура
и т. п.), если они не изменяют ее
электропроводность.
Электромагнитные
расходомеры можно монтировать в любом
положении на расстояниях, равных не менее
20 диаметров трубопровода после местных
сопротивлений, нарушающих осесимметричное
течение среды, и не менее восьми диаметров
до местных
сопротивлений.
Конструкция
первичных преобразователей позволяет
применять новейшие изоляционные,
антикоррозийные и другие покрытия, что дает
возможность измерять расход агрессивных и
абразивных сред.
Отмеченные
преимущества и обеспечили достаточно
широкое распространение электромагнитных
расходомеров, несмотря на их относительную
конструктивную сложность и необходимость
тщательного каждодневного технического
ухода (подрегулировка нуля,
поднастройкаит.п.).
Электромагнитные
расходомеры применяют для измерения очень
малых (3 • 10-9 м3/с)
расходов (например, для измерения расхода
крови по кровеносным сосудам) и больших
расходов жидкостей (3 м3/с). Причем
диапазон измерения расходомера одного
типоразмера достигает значения 10:1,
т. е. достаточно
велик.
Электромагнитные расходомеры
непригодны для измерения расхода газов, а
также жидкостей с электропроводностью
менее 10-3— 10-5 сим/м
(ДО–5—10-7
Ом–1-см-1), например,
легких нефтепродуктов, спиртов й т. п.
Применение разрабатываемых в настоящее
время специальных автокомпенсирующих
устройств позволит существенно снизить
требования к электропроводности
измеряемых сред и создать электромагнитные
расходомеры для измерения расхода любых
жидкостей, в том числе и
нефтепродуктов.
7.5.
Ультразвуковые
расходомеры
Принципиальная схема
ультразвукового расходомера приведена на
рис. 69. Звуковые колебания высокой частоты
(20 кГц и выше), создаваемые
электроакустическим вибратором
(излучателем) И1, проходят через текущую
по трубопроводу среду и регистрируются
приемником
П1, отстоящим от
излучателя на ————|—тшшшш
расстояние L. Если v —
скорость
V
потока среды, а с —
скорость
——–звука в данной среде,
то про-
Щ(П2)~ I—I
П1(и2) Д°лжитепьность
распространения
^——–‘ „
звуковой волны по
направлению
движения потока от
излучателя И1 до приемника
П1
Рис. 69. Принципиальная схема
ультразву- _
(7.24)
кового расходомера
с
v
Продолжительность же
распространения звуковой волны против
движения потока от излучателя И2 до
приемника П2
тг = —^-
. (7.25)
С—V
Не трудно
убедиться, что на основании формул (7.24) и (7.25)
разность тг —Т, измеряемая
электронно-счетной схемой,
Ат =
^—irV— •
(7–26)
г
Приняв
во внимание, что v2/c2
пренебрежимо мала по сравнению с единицей
(например, для жидкостей, у которых с =
1000—1500 м/с, a v не превосходит 6—8 м/с,
v2/c2 <6 •
10_s), и выразив скорость потока
через расход, получим уравнение измерений
ультразвуковых расходомеров
Дт =
2<р ^гг~ & (7.27)
где
F – площадь сечения потока; <р —
коэффициент, учитывающий распределение
скоростей по сечению
потока.
Существуют различные
способы и различные измерительные схемы
для определения Дт:
1)
измерение разности фазовых
сдвигов ультразвуковых волн, направляемых
по потоку и против него;
2)
измерение разности частот
повторения коротких импульсов или пакетов
ультразвуковых колебаний, направляемых
одновременно по потоку и против
него;
3) измерение разности
длительности прохождения коротких
импульсов, направляемых одновременно по
потоку и против него.
Кроме того,
имеется самостоятельный метод определения
расхода, основанный на измерении смещения
потоком ультразвуковой волны, направляемой
перпендикулярно к направлению движения
среды.
Основные трудности
практического использования
ультразвуковых расходомеров связаны с тем,
что, во-первых, скорость распространения
звука зависит от физико-химических свойств
измеряемой среды (ее температуры, давления,
концентрации и т. п.) и, во-вторых, она
несоизмеримо больше скорости движения этой
среды. Первое из отмеченных обстоятельств
приводит к необходимости применения в
ультразвуковых расходомерах специальных
методов и средств компенсации влияний
свойств среды, второй — к необходимости
использования дифференциальных схем
измерений (для выделения „слабого”
полезного сигнала). И то, и другое
обусловливает большую сложность
измерительной аппаратуры.
Кроме
того, показания ультразвуковых
расходомеров зависят от числа Рейнольдса.
Это объясняется тем, что они измеряют не
действительную среднюю скорость потока, а
среднюю скорость по линии ультразвукового
луча. Соотношение между этими скоростями
является функцией числа
Рейнольдса.
Несмотря на это,
ультразвуковые расходомеры все более
широко применяют в нефтехимической,
пищевой и других отраслях промышленности,
при гидравлических исследованиях и
испытаниях гидромашин. Достоинствами их
являются:
возможность
бесконтактного измерения любых сред, в том
числе и
неэлектропроводных;
достаточно
высокая точность приборов при их
индивидуальной градуировке и
использовании специальных средств
автокомпенсации наиболее существенных
помех (известны ультразвуковые
расходомеры, основная погрешность которых
не превышает 0,3 % верхнего предела
измерений) ;
высокая надежность
чувствительных элементов (излучателей и
приемников ультразвуковых колебаний),
представляющих собой круглые пластинки
кварца или титаната бария, устанавливаемые
снаружи трубопровода или защищенные от
непосредственного контакта с измеряемой
средой металлическим (пластмассовым)
звукопроводом;
высокое
быстродействие, позволяющее измерять
пульсирующие расходы с частотой пульсаций
до 10 ООО Гц.
Чувствительность
ультразвуковых расходомеров зависит от
отношения v/с. Чем больше зто отношение,
тем больше чувствительность прибора и тем
меньше погрешности измерений. Из
сказанного следует, что данные приборы
более пригодны для измерения расхода газов,
чем жидкостей, так как значение v/c у
газов значительно больше. Однако в
настоящее время ультразвуковые
расходомеры преимущественно применяются
для измерения расхода жидкостей. Это
объясняется тем, что акустическое
сопротивление (рс) газов мало. Поэтому
ультразвуковым колебаниям в газе трудно
сообщить энергию, необходимую для переноса
волны от излучателя до приемника, поскольку
количество энергии, отбираемой средой от
излучателя, пропорционально акустическому
сопротивлению среды.
Кроме того,
коэффициент поглощения звука для газов
значительно больше, чем для
жидкостей.
7.6. Оптические
(лазерные) расходомеры
К числу
сравнительно новых, но быстро
развивающихся методов измерения локальных
скоростей потока и расхода относятся
методы, основанные на применении
оптических квантовых генераторов—лазеров
(ОКГ). Достоинствами этих методов являются:
бесконтактность, высокая чувствительность,
малая инерционность, большой диапазон
измерений скоростей и расходов независимо
от физических свойств измеряемой среды (как
жидкостей, так и газов), за исключением
требования ее прозрачности в диапазоне
длин волн, излучаемых квантовыми
генераторами.
Наиболее перспективно
применение оптических методов в
экспериментальной гидродинамике, особенно
в области турбулентных явлений, изучение
которых традиционными способами (например,
с помощью термоанемометров) уже не дает
желаемых результатов вследствие малой
точности приборов и, главное, вносимых ими
искажений в изучаемую структуру
потока.
Кроме того, лазерные
расходомеры используют при измерении
расхода агрессивных, высоко- и
низкотемпературных (криогенных) жидкостей
и газов.
Б настоящее время
распространение получили две
конструктивные разновидности оптических
(лазерных) расходомеров,. отличающихся
лежащими в их основе физическими явлениями:
расходомеры, основанные на эффекте
рассеяния света движущимися частицами
(допплеровские расходомеры), и расходомеры,
основанные на эффекте Физо-Френеля —
увлечения света движущейся средой.
Б
оптическом расходомере (назовем его
сокращенно ДИС), реализующем первый эффект,
излучение лазера, рассеянное движущимися в
потоке естественными или искусственно
введенными частицами, приобретает
частотный сдвиг, пропорциональный
осредненной скорости
частиц.
Принципиальная схема ДИС
показана иа рис. 70. Прибор работает
следующим образом. Световой поток,
излучаемый газовым лазером 1, делится
расщепителем 2 на два параллельных
пучка равной интенсивности, которые линзой
3 фокусируются в исследуемой области
среды, движущейся по трубопроводу 4. В
области пересечения лучей возникает
пространственная интерференционная
картина из чередующихся светлых и темных
полос. Перемещающиеся в этой области
частицы перекрывают светлые полосы, в
результате чего рассеянный частицами свет
модулируется частотой, пропорциональной
скорости движения
частиц.
Рассеянный свет
улавливается приемной оптической системой
5 и направляется на фото детектор 7.
Выделение и регистрация, частотного
сигнала (пропорционального скорости
движения частиц) осуществляется
анализатором спектра или автоматической
следящей системой 8. Диафрагма 6
предохраняет фотодетектор от фонового
излучения.
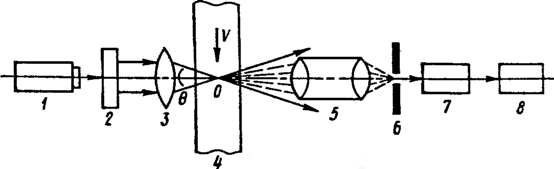
Рис.
70. Принципиальная схема лазерного
измерителя скоростей
Для создания
рассеивающих центров (зоны движущихся
частиц) в жидкостях в настоящее время чаще
всего используют полистироловые шарики
диаметром 0,5—1,0 мкм, добавляемые в поток с
объемной концентрацией 0,002—0,02 %. Для
получения сигнала требуемой интенсивности
в газах достаточно 0,15 • 10-3
кг/м3 взвешенных примесей и
аэрозоля. Эффективным способом получения
рассеивающих центров в газах является
способ распыления жидкостей (например,
воды).
Основными источниками
методических погрешностей ДИС являются:
неравномерность профиля скоростей потока;
турбулентные пульсации скоростей;
неоднородность рассеивающих частиц и их
„проскальзывание” (несовпадение
скоростей) относительно основного
потока.
Эти погрешности совместно с
аппаратурными обусловливают суммарную
погрешность измерений расхода с помощью
ДИС порядка 1,5— 2,0%.
Принципиальная
схема расходомера, реализующего эффект
Физо-Френеля, показана на рис. 71. Основным
элементом расходомера является
гелиево-неоновый лазер, резонатор которого
образован зеркалами 1,
4, 5,
расположенными в вершинах треугольника, и
активным элементом
9. Лазер
генерирует две встречные волны, бегущие по
замкнутым оптическим путям. Поток жидкости
или газа, движущийся на некотором участке
резонатора по трубопроводу 2 с
прозрачными окнами 3, создает различные
по знаку приращения оптических путей
встречных волн лазера за счет составляющей
проекции вектора скорости потока на
направление луча. Вследствие этого
различны и частоты встречных
волн.
Часть энергии встречных лучей
выводится из резонатора и
зеркалами
6, 8 направляется на
фотодетектор 7, в цепи которого появляется
фототок разностной частоты биений,
пропорциональной скорости потока,
ос-редненной по пути
луча.
Инструментальная погрешность
описанных расходомеров определяется, в
основном, погрешностью измерения частоты
биений. Нестабильность частоты биений
вызывается механическими вибрациями,
изменением температуры окружающей среды, а
также процессами, происходящими в плазме
ОКГ. Известны „Физо-Френелевские”
расходомеры, основная погрешность которых
не превосходит 0,5 % верхнего предела
измерений.
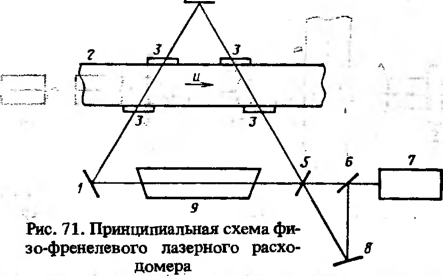
;
Методические погрешности этих
расходомеров обусловливаются
непостоянством показателя преломления
измеряемой среды и отличйем скорости,
осредненной по длине луча, от
действительной средней скорости потока
(аналогично, как у рассмотренных выше
ультразвуковых расходомеров)
.
Особенно перспективны данные
расходомеры для измерения расхода газов,
поскольку частота выходного сигнала при
показателях преломления, близких к единице
(что характерно для большинства газов),
пропорциональна массовому
расходу.
7.7. Измерение расхода
методом контрольных „меток”
Если
создать в потоке измеряемой среды
какую-либо „метку” (какой-либо
отличительный признак части потока, за
перемещением которого можно проследить) и
измерять время ?м, за которое эта
„метка” пройдет определенный
фиксированный путь Z,M, то, считая, что
скорость перемещения „метки” v равна
скорости потока,
получим
(7.28)
*М
Расходомеры,
основанные на этом методе измерений (рис. 72),
состоят из устройства, периодически
создающего ту или иную „метку” потока;
устройства, фиксирующего момент
прохождения „метки”, и прибора,
измеряющего продолжительность перемещения
„метки” на фиксированное расстояние
Ьы.
На основании формулы
(7.28) уравнение измерений зтих приборов
будет иметь вид
=
(7-29)
v
—
1н
Рис. 72. Схема
измерения расхода методом контрольных
„меток”
где кр — коэффициент,
зависящий от распределения скоростей по
сечению потока и числа
Рейнольдса.
Погрешности измерения при
данном методе не нормируются. Метод, как
правило, используется в лабораторных
условиях для измерения расхода газа при
сверхвысоких скоростях, т. е. там, где другие
методы трудно применить.
Й
контрольному вопросу №
13
Действительно, „закрутка” потока,
вызванная сопротивлением первой турбинки,
оказывает тормозящее действие на
вторую.
7.8. Расходомеры, основанные на
явлении
ядерного магнитного резонанса
(ЯМР-расходомеры)
Поляризованные в
постоянном магнитном поле атомные ядра
большинства элементов, помещенных в
переменное осциллирующее поле, при угловой
частоте осциллирующего поля, равной
угловой скорости прецессии (колебаний
относительно среднего положения) ядер
(ларморовой частоте), взаимодействуют с ним,
поглощая часть его энергии. При этом
изменяется намагниченность ядер, т. е.
суммарный магнитный момент ядер в единице
объема вещества.
Это явление — явление
взаимодействия поляризованных ядер с
резонансным осциллирующим шлем называется
ядерным магнитным
резонансом.
Существует несколько
принципов построения расходомерных
устройств, основанных на ядерном магнитном
резонансе. Во-первых, явление ядерного
резонанса используется для создания
„меток” в потоке жидкости.
Схема
ЯМР-расходомера, работающего на принципе
контрольных „меток”, показана на рис. 73.
Жидкость проходит через магнитное поле,
создаваемое магнитом 1 и поляризуется
(ядра жидкости
ориентируются
относительно силовых
линий поля, что обусловливает ее
намагниченность). Протекая через катушку
2, на которую подается от генератора
5 переменное напряжение резонансной
частоты, поляризованные ядра жидкости
поглощают часть энергии осциллирующего
поля, создаваемого катушкой, и жидкость
деполяризуется. При периодическом
отключении тока, Рис. 73. Схема
ЯМР-расходомера, рабо- питающего катушку 2, в
потоке тающего на принципе контрольных
меток жидкости на выходе из катушки
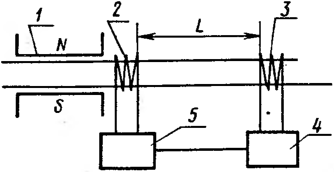
будут создаваться пакеты
поляризованных молекул. Эти молекулы,
пройдя фиксированное расстояние L,
попадают в катушку 3, которая также
питается переменным напряжением
резонансной частоты. В моменты протекания
поляризованных молекул через
осциллирующее поле катушки 5 в ее цепи будет
возникать сигнал ядерного магнитного
резонанса, фиксируемый измерительной
схемой 4. Таким образом, в данном случае
измерение расхода сводится к измерению
времени между моментом отключения
напряжения от катушки 2 и моментом
появления сигнала ядерного магнитного
резонанса в схеме 4, связанной с
катушкой 3. Уравнение измерений
расходомеров данного типа не отличается от
уравнения измерений метода контрольных
„меток” (98).
Другой принцип работы
ЯМР-расходомеров основан на зависимости
амплитуды сигнала ядерного резонанса А
от скорости течения жидкости V, открытой
индийским ученым Сурианом
А-А А
о
![]()
(7.30)
где
А0 — амплитуда сигнала ядерного
резонанса в неподвижной жидкости; fp —
постоянное для данной жидкости время
продольной релаксации ядер; I – длина
датчика, создающего резонансное
поле.
Пользуясь выражением (7.30), рабочее
уравнение данного типа ЯМР-расходомеров
можно представить в
виде
Q=fC(~7— 1)
(7.31)
¦Л0
где постоянная К =
lF/tp; F — калибр
расходомера.
Принципиальная схема
такого расходомера показана на рис. 74.
Участок трубопровода помещен в сильное
поляризующее поле. На концах участка
монтируется датчик ядерного магнитного
резонанса, на катушку которого подается
переменное напряжение резонансной частоты.
Поляризованная жидкость, протекая через
датчик, дает сигнал ядерного резонанса,
амплитуда которого зависит от расхода
жидкости. Подобное устройство можно
применять для измерения расхода жидкостей
с большим количеством ядер (например,
жидкости, содержащие водород или фтор),
обеспечивающим достаточно большой сигнал
ядерного резонанса. Концентрация рдер
должна сохраняться постоянной, в
противном случае будет изменяться
чувствительность прибора. Концентрация
ядер пропорциональна плотности, а
следовательно, погрешность показаний
прибора зависит от всех факторов
(температуры, давления, концентрации и т. п.),
влияющих на плотность измеряемой среды.
Кроме того, погрешность показаний
существенным образом зависит от качества
стабилизации питающего напряжения и
наличия внутренних (схемных) и внешних
(вызываемых турбулентностью потока) шумов.
При аппаратурном подавлении этих шумов (что
ведет к большой сложности измерительной
схемы) погрешность ЯМР-расходомеров при их
градуировке на реальной измерят емой среде
может быть сведена к погрешности порядка
0,5—1,0% верхнего предела измерений.
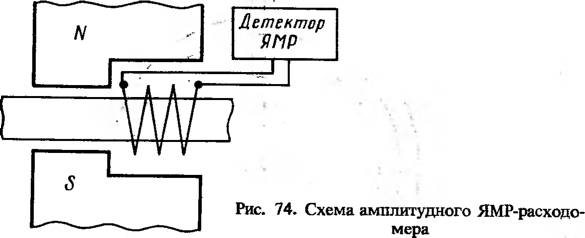
К
достоинствам ЯМР-расхоДомербв (значительно
окупающим их конструктивную сложность)
относят: высокую чувствительность и малый
нижний диапазон измерений; бесконтактность
измерений; нечувствительность к перемене
ориентировки трубопровода в пространстве;
линейность шкалы и возможность
использования их в системах контроля и
регулирования в связи с малой
инерционностью и электрическим выходным
сигналом датчика в виде напряжения низкой
частоты.
В настоящее время
ЯМР-расходомеры применяются в основном при
лабораторных исследованиях, в биологии и
медицине (для измерения расхода крови).
7.9. Центробежные
расходомеры
Центробежный расходомер
(рис. 75) представляет собой 360-градусное
колено (т. е. полную окружность)
трубопровода, в верхней части которого на
внешней и внутренней (по радиусу кривизны)
стенках отбирают давления рг и
рх соответственно. Ранее
применялись и 90-градусные колена, но они не
обеспечивали достаточной точности
измерений, поэтому в настоящее время
рекомендовано применять 360-градусные
колена.
Принцип действия центробежных
расходомеров основан на том, что при
движении среды по криволинейному участку
трубопровода появляются центробежные силы,
создающие перепад давлений между точками с
разными радиусами кривизны (где кривизна
больше, там и центробежная сила больше и
больше давление на стенку).
Полученные
из условия равенства гидростатической и
центробежной сил, действующих на элемент
объема среды, текушей по криволинейному
участку трубопровода (с радиусом кривизны
его геометрической оси Ro) рабочие
уравнения измерений центробежных
расходомеров имеют вид:
для капельных
жидкостей
для газов
Q = -fr
г^0г у/ In -?а-
(7.33)
р 2 р рг
гдег
— внутренний радиус (см. рис. 77)
трубопровода; р0 — 1/2 (pi Рг) ; ф
— корректировочный коэффициент,
зависящий от вязкости измеряемой среды и
шероховатости трубопровода; f —
коэффициент, характеризующий степень
неиэотермичности процесса сжатия газа в
цилиндрическом колене.
При Р2/Р1 <2 как
для жидкостей, так и для газов с достаточной
для практики точностью можно использовать
формулу (7.32).
Как показали широкие
экспериментальные исследования
американских прибористов В. Лансфорда, Д.
Картеля и др., коэффициенты ф, f при
прямолинейном участке трубопровода перед
360-градусным коленом расходомера, большем
2R0, стабильны и мало (на 1,0—1,5 %)
отличаются от единицы в весьма широком
диапазоне изменения вязкости измеряемой
среды и ее расхода, что может быть объяснено
малостью сил трения по сравнению с
центробежными силами.
Отмеченное
обстоятельство позволяет сделать вывод о
возможности косвенной (расчетной)
градуировки центробежных расходомеров с
круговым коленом го результатам измерений
технологически качественно выдержанных
геометрических параметров Ro и г. При
этом их основная погрешность может быть
„уложена” в ±2,0—2,5 % верхнего предела
измерений, что соответствует точности
расходомеров с сужающими
устройствами.
Существенным
достоинством центробежных расходомеров
является и малая степень влияния
пульсационных характеристик потока на их
показания. Действительно, так как давления
рi и р2 отбираются в одном
сечении
потока (а не в разных, как у сужающих
устройств) постоянные по сечению
пульсационные составляющие будут
компенсироваться при измерении разности
давлений.
Простота и надежность
центробежных расходомеров позволяет
применять их в сложных эксплуатационных
условиях, характерных для технологических
процессов в нефтяной, газовой и химической
промышленности.
7.10.
Вихревые и гидродинамические
расходомеры
Вихревые расходомеры
сравнительно новые приборы, применяемые
для измерения расхода жидкостей и газов с
широким диапазоном изменения
физико-химических свойств. Принцип
действия этих расходомеров заключается в
создании (с помощью винтообразных шнеков) в
потоке движущейся по трубопроводу среды
устойчивого периферийного вихря.
Центральная часть потока (вблизи оси
трубопровода) при зтом приобретает
характер винтового шнура. Если
сформированный таким образом поток пустить
через расширяющийся насадок, то
периферийные вихреобразования теряют
устойчивость, а центральный шнур начинает
прецессировать (колебаться) относительно
геометрической оси насадка с частотой,
пройорциональной средней скорости потока,
и амплитудой, равной диаметру выходной
части насадка. С аналогичной частотой и
амплитудой, равной скоростному напору
pv2, будет изменяться при этом и
давление на выходе потока из насадка.
Преобразовав с помощью
ампли-тудно-частотного датчика (например,
струнного) пульсации давления в
электрический сигнал и поделив его
амплитудное значение на частотное, получим
величину, значение которой пропорционально
массовому расходу вещества. Для нахождения
объемного расхода достаточно измерить
частотную составляющую
сигнала.
Погрешность вихревых
расходомеров при их индивидуальной
градуировке на реальной измеряемой среде
не превосходит 1,5—2,0
%.
Гидродинамические расходомеры
основаны на измерении лобового давления
(рп) движущейся среды,
действующего на помещенное в поток
тело.
На рис. 76 показаны схемы различных
типов гидродинамических расходомеров,
отличаюйдахся друг от друга формой тела,
воспринимающего гидродинамическое усилие
R = слр v2cp/2 (f — площадь
миделево-го сечения тела — проекции тела на
плоскость, перпендикулярную к направлению
потока) и способом измерения
гидродинамического усилия.
Для
расходомеров с поворотным крылом (рис. 76,
а) и поворотным диском (рис. 76, б) мерой
расхода является поворот крыла или диска
относительно оси вращения. Уравнение
измерений этих приборов, полученное из
условия, равенства моментов
гидродинамической силы и веса крыла (диска),
имеет вид
![]()
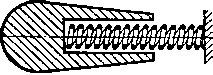
уШ/7//7/////У?/УУУУ/УУУУ/УУУУУУ//УЛ
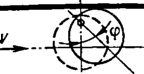
в
Рис. 76.
Гидродинамические расходомеры
где F
— площадь сечения трубопровода; / —
площадь наибольшего сечения крыла или
диска; G — вес крыла или диска;
сл — коэффициент лобового
сопротивления, зависящий от формы и
размеров тела обтекания (в данном случае
крыла или диска) и чисел Рейнольдса. В
расходомере с каплевидным телом обтекания
(рис. 76, б) мерой расхода является деформация
упругой пружины, а следовательно, и осевое
перемещение I тела обтекания. Уравнение
измерений этих приборов имеет вид
![]()
слр/
(7.35)
где
с — жесткость пружины.
Иногда и
первые два типа гидродинамических
расходомеров снабжаются упругими
элементами в виде пластинчатых или
струнных пружин.
Зависимость сл от
большого числа изменяющихся и
неконтролируемых в процессе измерений
параметров, нестабильность поля скоростей
набегающего потока при перемещении тела
обтекания являются источниками больших
погрешностей этих расходомеров. Вследствие
этого основные усилия их разработчиков
направлены на отыскание таких форм и
габаритных размеров тел обтекания, при
которых в достаточно широком диапазоне
изменений расхода обеспечивается
автомодельность (постоянство) сп.
Наиболее полно этим требованиям отвечают
крыловидные профили с перекрытием потока
порядка 0,5—0,6 и тела обтекания, выполненные
в вцде концентрических окружностей с
перемычками, наружный радиус которых
составляет 0,754 радиуса проточной части
трубопровода.
Достоинствами
гидродинамических расходомеров являются
их конструктивная простота, надежность и
удобство обслуживания. На сегодняшний день
их применяют в качестве индикаторов
расхода загрязненных жидкостей и
газов.
7.11. Приборы для
измерения расхода в единицах массы
(массовые расходомеры)
В системах
автоматического регулирования
теплоэнергетических установок, в ракетной
и авиационной технике, в различных
химических процессах массовый расхоц
{М) является основным физическим
параметром, определяющим оптимальные
режимы работы объектов и качество
процессов. В связи с этим в последнее время
у нас в стране и за рубежом интенсивно
разрабатываются и внедряются различные
приборы для измерения массового расхода.
Развитие этой области расходометрии идет
по трем направлениям. Во-первых, объемные
расходомеры (переменного перепада
давления, электромагнитные, турбинные и пр.)
снабжаются соответствующими датчиками
плотности и корректирующими схемами;
во-вторых, создаются приборы, способные
непосредственно измерять прямыми методами
массовый расход благодаря особенностям
своего принципиального устройства:
в-третьих, находят применение
комбинированные расходомеры, измеряющие
массовый расход косвенными методами путем
автоматической обработки результатов
прямых измерений связанных с ним
параметров.
Контрольный вопрос №
14
На показания какого типа
расходомеров – ультразвуковых или
ЯМР-расходомеров- изменения вязкости
измеряемой среды оказывают большее
влияние?
Если Вы решите, что на
показания ультразвуковых расходомеров —
см. с. 182, если на показания ЯМР-расходомеров
— см. с. 1S6.
К контрольному вопросу №
13
Вы неправильно ответили на
вопрос.
Разберитесь, что происходит
с потоком измеряемой среды при ее течении
через турбинный датчик, и как „закрутка”
потока влияет на показания турбинных
расходомеров.
Несмотря на
многообразие предложенных принципиальных
схем и конструктивных решений, массовые
расходомеры прямого действия можно отнести
к двум основным видам: инерционным и
тепловым. Принцип действия инерционных
расходомеров основан на том, что потоку
измеряемого вещества сообщается
дополнительное движение, чтобы создать в
потоке инерционные эффекты, по которым
судят о значении массового расхода. В
зависимости от того, какое именно
дополнительное движение сообщается потоку
(при помощи вращающегося или колеблющегося
звена), на чувствительном элементе прибора
возникает или усилие Кориолиса, или
гироскопический, или инерционный момент.
Принцип действия тепловых расходомерйв
основан на непрерывном нагреве потока
(калориметрические расходомеры) или
специального элемента, помещенного в поток
(термоанемометры). В первом случае массовый
расход определяется количеством тепла,
обеспечивающим определенную разность
температур потока до и после нагревателя;
во втором — количеством тепла, теряемым
нагретым или непрерывно нагреваемым телом,
помещенным в поток измеряемого
вещества.
Массовые турборасходомеры. В
турборасходомерах, реализующих
инерционный принцип измерений, закручивакй
поток относительно вектора его актуальной
(продольной) скорости.
Момент,
нюбходимый для обеспечения устойчивого
вращения потока с угловой Скоростью со,
определяется (без учета сил
гидравлического трения)
соотношением
Мвр =
Jсо, (7.36)
где / —
момент инерции среды.
Учитывая, что dJ
= R^drn (RK – радиус инерции; т –
масса вращающейся среды) и dm/dt =М (М –
массовый расход среды), из выражения (7.36)
получим общее для всех турборасходомеров
уравнение для определениям
мвр
При торможении
предварительно закрученного потока на
тормозящее устройство будет действовать
момент, соответствующий выражению (7.29), и
уравнение приборов, использующих эффект
торможения закрученного потока, не будет
отличаться от выражения (7.37).
Существует
большое число различных модификаций
турбинных датчиков массового расхода,
отличающихся способами вращения потока,
измерения Мвр и значениями
RK.
Принципиальные схемы
датчиков, получивших преимущественное
распространение, приведены на рис.
77.
Основным источником методических
погрешностей турборасходомеров является
непостоянство сил трения в их
гидравлическом тракте, обусловленное
изменениями вязкости, температуры и других
параметров измеряемой
среды.
Погрешность измерения массового
расхода турборасходомерами может бьггь
доведена до ±(0,5—1,0) % верхнего предела
измерений. Повышение точности лимитируется
трудностями поддержания постоянного числа
оборотов ведущей (закручивающей поток)
турбинки, нестабильностью характеристик
упругих элементов, воспринимающих действие
инерционного звена, и изменением КПД
приводного двигатедя при изменении
нагрузки (расхода). Кроме того, на показания
турборасходомеров (как уже отмечалось выше)
влияет изменение параметров измеряемой
среды, а их надежность ограничивается
наличием изнашивающихся
опор.
Корнолисовые и гироскопические
расходомеры. В этих расходомерах
закручивание и торможение потока
производится в помощью вращающихся
элементов трубопровода сложной
конфигурации.
Кориолисовый расходомер
(рис. 78) состоит из двух Т-образных участков
2 и 6 трубопровода, сочлененных при
помощи гибких соединений 1 и приводимых
во вращение с постоянной угловой скоростью
со специальным приводным механизмом.
Прибор размещен в корпусе 5 (показан
условно). При протекании вещества со
скоростью v через вращающийся в
уплотнительных муфтах 4 элемент
трубопровода в потоке возникает
направленное против вращения ускорение
Кориолиса, равное
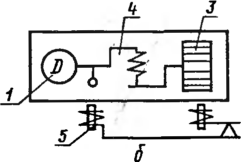
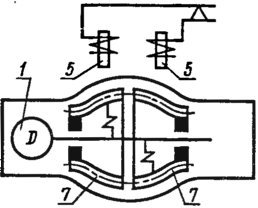
Рис. 77. Принципиальные схемы
наиболее распространенных датчиков:
а — измеряется мощность,
необходимая для закручивания потока;
б — измеряется момент вращения по
углу поворота упругой муфты; в — измеряется
момент вращения заторможенной крыльчатки
по углу ее поворота при упругом зацепле*
нии; г — измеряется разность углов
поворота двух крыльчаток, упруго
закрепленных на валу двигателя; д —
измеряется относительный угол поворота
двух крыльчаток с разными углами поворота
лопастей; 1 — двигатель; 2 —
датчик мощности; 3 — прямолопастная
крыльчатка; 4 — упругое соединение
валов; 5 — импульсный датчик; 6
— датчик угла поворота; 7 — радиальная
крыльчатка; 8 — спиральная
крыльчатка
а = 2сж Вследствие этого в
каждой ветви Т-образного участка создается
усилие RK = —m2ojv – —2Mco(i?2 — /?i)
и на всем вращающемся участке возникает
момент
Мк = 2RK =
2Д/со (Rl – Я?). (7.38)
В
результате действия этого момента
Г-образные участки, деформируя гибкое
соединение 1, поворачиваются
относительно друг друга на некоторый угол
а. Угол поворота а преобразуется в
электрический сигнал при помощи
торсионного датчика 3. Значение этого
сигнала пропорционально Мк, а
следовательно, при постоянной угловой
скорости вращения и массовому расходу
вещества.
Гироскопический расходомер
(рис. 79) состоит из эксцентрично
расположенных элементов трубопровода
сложной конфигурации. Устрой-
Рис. 78.
Схема кориолисова расходо- Рис. 79. Схема
гироскопического рас-меРа
ходомера
ство приводится во
вращение относительно оси АА с
постоянной угловой скоростью. Возникающий
при этом гироскопический момент
Мт стремится повернуть ротор
относительно оси ВВ.
Величина
Мг = 2Мы (Ri-R^b
(7.39)
пропорциональна массовому
расходу вещества и преобразуется в
соответствующий сигнал с помощью датчиков
деформации (например,
тензо-метрических).
Относительно
невысокая точность кориолисовых и
гироскопических расходомеров,
характеризуемая приведенной погрешностью
1—2 %, объясняется большими температурными
влияниями на жесткость упругих элементов,
их гистерезисом и последействием, а также
трудностями поддержания постоянным числа
оборотов приводного механизма, особенно
при колебаниях расхода. Расходомеры
данного типа громоздки, сложны в
эксплуатации, требуют специальных
вращающихся уплотнительных устройств и
большой мощности приводного
механизма.
Два последних недостатка
отсутствуют у вибрационных расходомеров, у
которых вращательное движение
трубопровода заменяется колебательным.
Однако точность вибрационных расходомеров
получается меньшей.
Преимуществом
кориолисовых и гироскопических
расходомеров является полная
независимость их показаний от вязкости
измеряемой среды. Поэтому их целесообразно
применять лишь для измерения массового
расхода веществ с большим диапазоном
изменения вязкости.
Калориметрические и
термоанемомегрические расходомеры. Если
пренебречь теплом, отдаваемым потоком
через стенки трубопровода в окружающую
среду, то уравнение теплового баланса Между
расходом тепла, потребляемым нагревателем,
и теплом, сообщенным потоку, принимает
вид
Qt = *о М.ср
АТ,
(7.40)
где к0
— поправочный множитель на
неравномерность распределения температур
по сечению трубопровода; ср —
теплоемкость (для газа при постоянном
давлении) при температуре Тг
7’2/2; Т[, Т2 — температуры
потока до и после нагревателя; АТ —
Т2 – Т.
Тепло к потоку в
калориметрических расходомерах подводится
обычно электронагревателями, для
которых
qt = 0,24pR,
(7.41)
где I — сила тока; R —
сопротивление нагревателя.
На основании
выражений (7.40) и (7.41) получим уравнение
измерений (статическую характеристику
преобразования) калориметрических
расходомеров
![]()
(7.42)
Возможны
и существуют два способа измерения
массового расхода в соответствии с
выражением (7.42) :
расход определяют по
значению мощности, потребляемой
нагревателем и обеспечивающей постоянную
разность температур АТ
расход
определяют по разности температур АТ
при неизменной мощности, подводимой к
нагревателю.
В первом случае
расходомеры работают как регуляторы
температуры нагрева потока, у которых
измерительным и регулирующим элементом
является уравновешенный мост с
термометрами сопротивления до и после
нагревателя. При изменении разности
температур мост выходит из равновесия и
включает устройство, которое изменяет
регулировочное сопротивление до тех пор,
пока не восстановится заданная степень
нагрева. Массовый расход при этом
определяют по показаниям ваттметра,
включенного в цепь нагревателя.
Датчики
калориметрических расходомеров второго
типа (рис. 80) состоят из двух
последовательно соединенных термометров
сопротивления 1 и 3, устанавливаемых
до и после нагревателя 2.
Последовательное соединение термометров
обеспечивает равенство токов в их цепях,
что позволяет градуировать rix
непосредственно по разности температур.
Кроме термометров сопротивления
используют также термисторы и термопары.
Термометры сопротивления обладают тем
преимуществом, что их можно выполнять в
виде равномерной сетки,.перекрывающей все
сечения потока, и таким образом измерять
среднюю по сечению температуру.
j
Калориметрические
расходомеры
=2s==j обладают
достаточно высокой точ–УУ1 – ностью,
оцениваемой (в условиях индивидуальной
градуировки) приведенной погрешностью ±
(0,5—1,0) %, большим диапазоном измерений (10:1 и
выше), малой инерционностью.
Недостатками их являются
сложность измерительных схем и
нестабильность характеристик, связанная с
коррозией приемных устройств и осаждением
на них различных частиц, переносимых
потоком.
Дачные приборы можно применять
для измерения массового расхода как
жидкостей, так и газов. Но в настоящее время
ими измеряют, главным образом, малые (в
трубках диаметром 2—3 мм) и средние расходы
чистых газов.
Статическая
характеристика преобразования (уравнение
измерений) термоанемометров определяется
известным уравнением теплофизики
Qt =
0,2412В = (Тн – Тс) (X V
2тгс,.сГ V’vp” ), (7.43)
где
Тн — температура тела;
Тс — температура потока
измеряемой среды; X — теплопроводность
среды; с„ — теплоемкость среды при
постоянном объеме; d — диаметр
нагреваемого тела.
Термоанемометры
измеряют „массовую” скорость vp потока
в месте установки нагреваемого тела.
В
последние годы появились бесконтактные
термоанемометрические расходомеры, в
которых роль термоэлемента играет
изолированный участок трубопровода.
Как
видно из уравнения (7.43), „массовую”
скорость при помощи термоанемометра можно
измерять двумя способами. В одном случае
ток, нагревающий приемник, поддерживают
постоянным, и скорость определяют по
результатам измерения его температуры. В
другом случае ток нагрева регулируют таким
образом, чтобы температура приемника
оставалась постоянной, а скорость
определяют по значению питающего тока. В
практике встречаются оба этих способа
измерений.
Приемник термоанемометра
(термонить) обычно выполняют из платиновой
проволоки диаметром 0,005—0,3 мм. Температура
термонити должна быть по возможности
высокой, так как при ее увеличении
повышается чувствительность приемника и
уменьшается влияние колебаний температуры
потока. Однако значительное повышение
температуры проволоки может вызвать
изменение структуры металла и тем самым
„снос” градуировочных кривых
прибора.
Основным недостатком
термоанемометров является существенное
влияние на их показания температуры,
давления и различных теплофизических
параметров измеряемой среды.
В связи с
очень малыми габаритными размерами
приемника (термо-нити) приборы получили
преимущественное распространение в
лабораторно-экспериментальной практике
при измерении скоростей в тончайших
пристенных слоях и пленках жидких и
газообразных потоков. До появления
оптических (лазерных) методов
термоанемометры были единственными
приборами, позволяющими проводить такие
измерения.
Погрешности
термоанемометров до настоящего времени
полностью не изучены, и точность
выполняемых с их помощью измерений не
нормируется.
Комбинированные
турбопоршневые расходомеры. Одним из
примеров, иллюстрирующим возможность
комбинированного измерения массового
расхода, являются турбопоршневые
расходомеры, состоящие иэ турбинного с
аксиальной крыльчаткой и поршневого
преобразователей. Угловая скорость
вращения турбинки пропорциональна
объемному расходу среды, протекающей по
трубопроводу,
со = &i Q.
(7.44)
Поршневой преобразователь
воспринимает и передает на регистрирующий
или показывающий прибор гидродинамическое
давление потока, действующее на ступицу
турбинки и равное
р — кърй2,
(7.45)
где hi, к2 —
коэффициенты пропорциональности, в общем
случае зависящие от числа Рейнольдса и
конструктивных параметров
преобразователей.
Поделив выражение (7.45)
на выражение (7.46), т. е. поделив показания
поршневого преобразователя на показания
турбинного, получим рабочие уравнения
измерений турбопоршневых расходомеров.
Так, при измерении массового
расхода
М=Ам-Е-,
(7.46)
СО
тцеАм =
hi/кг;
при измерении плотности
протекающей среды
P=Ap-Ej,
(7.47)
me Ар
=кЦк2
Используя формулы (7.46) и
(7.47), по результатам измерений угловой
скорости и гидродинамического давления при
известных (определенных в процессе
градуировки приборов) коэффициентах
Ам и Арможно рассчитать
значения массового раЬхода и плотности
протекающей среды.
Турбопоршневой
расходомер (рис. 81) работает следующим
образом. Турбинка 11 жестко закреплена
на поршне 8, который может перемещаться
вдоль оси и вращаться относительно
неподвижного цилиндра 9, закрепленного
в опоре 10. Все детали прибора помещены в
корпусе 2.
В цилиндре 9 создается
давление, пропорциональное статическому
давлению в потоке и гидродинамическому
напору, действующему на турбинку 11 и
поршень 8 в аксиальном направлении. Это
давление по трубке 7, заполненной
специальной манометрической жидкостью,
передается в одну из полостей
дифференциального манометра 5. Во
вторую полость дифманометра по трубке 4
подается статическое давление, отбираемое
из кольцевой
Рис. 81. Схема
турбопоршневого расходо- камеры 3.
Следовательно, диф-мера
манометр 5 будет измерять
толь
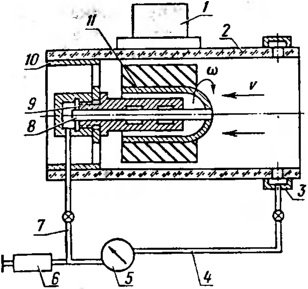
ко динамическую составляющую
давления потока, действующую на
поверхность турбинки и выражаемую формулой
(7.45). Поршневая пара 8—9 имеет микронные
зазоры, что обеспечивает чисто жидкостное
трение в поршневом датчике и весьма малые
утечки манометрической жидкости,
заполняющей систему дифманометра. Для
пополнения утечек в систему введен пресс
6. Угловая скорость вращения турбинки
измеряется счетным устройством
1.
Основными достоинствами
турбопоршневых расходомеров
являются:
возможность одновременного и
комплексного измерения объемного,
массового расхода и плотности протекающей
по трубопроводу среды;
высокая точность
измерений, обусловленная объединением в
этих приборах двух прецизионных
измерительных преобразователей —
турбинного и поршневого и характеризуемая
погрешностями измерений объемного расхода
0,1—0,2 %, массового расхода и плотности 0,3—0,5
%;
отсутствие опор с сухим трением, а
следовательно, высокая стабильность и
надежность турбопоршневых
приборов.
Специфическим недостатком
данных расходомеров являются утечки
манометрической жидкости в измеряемую
среду. Однако эти утечки могут быть сведены
к ничтожно малым известными и применяемыми
в системах с неуплотненным поршнем
конструктивными мероприятиями. При
измерении же расхода нефтепродуктов и
других жидкостей, которые могут быть
использованы в поршневых системах при
соответствующем подборе материалов
поршневых пар в качестве манометрических,
этот недостаток вообще не сказывается.
В
связи с достаточно высокой точностью и
надежностью турбопорш-невые расходомеры
используют в настоящее время’ в качестве
образцовых расходоизмерительных
устройств.
Естественно, возможны и
другие комбинированные системы для
измерения массового расхода, например,
одновременное использование сужающего
устройства и турбинного датчика и пр.
Однако точностные возможности этих систем
получаются существенно меньшими.
7.12.
Техника измерения расхода жидкостей и
газов в трубопроводах больших
диаметров
Проблема измерения расхода в
трубопроводах больших диаметров (свыше 1 м)
является самостоятельной
расходоизмерительной проблемой, которая
решается своим специфическим путем. Это
обусловливается тем, что использование для
зтих целей расходомеров, реализующих
традиционные методы (описанные в
предыдущей главе), требует колоссальных
затрат как на создание самих приборов, так и
на создание средств их индивидуальной
градуировки и поверки, которые в настоящее
время практически полностью
отсутствуют.
Последнее обстоятельство и
определяет, в основном, те специфические
требования, которые предъявляются к
методам и средствам измерения расхода в
трубопроводах больших
диаметров:
возможность косвенной
(расчетной) градуировки без применения
расходомерных стендов и
установок;
инвариантность
(независимость) градуировочных
характеристик к диаметру трубопровода или
возможность их пересчета с малых диаметров
(для которых имеются образцовые установки)
на сколь угодно большие.
Контрольный
вопрос № 15
При некоторых режимах
работы сечение технологического
трубопровода диаметром 100 мм лишь
частично заполняется текущей жидкостью
(трубопровод в месте установки расходомера
„работает” неполным
сечением).
Какой из известных Вам
типов расходомеров Вы бы выбрали для
измерений при этих условиях?
Ответ
на этот общий по гл. 7 вопрос дан в конце гл.
8.
К контрольному вопросу №
14
Вы правильно ответили на
вопрос.
Действительно, показания
ультразвуковых расходомеров зависят от
распределения скоростей по сечению потока,
которое в свою очередь зависит от числа
Рейнольдса и, следовательно, от вязкости. В
то же время, как следует из принципа
действия и рабочего уравнения
ЯМР-расходомеров, изменения вязкости
измеряемой среды не влииют на их
показания.
Парциальный метод
измерения расхода основан на измерении
расхода определенной части основного
потока,1 отведенной в байпасную или
обводную трубку.
Часть потока отводится
обычно при помощи сужающего устройства,
установленного в трубопроводе так, как это
показано на рис. 82.
Для измерения расхода
в байпасной трубке можно применять любой из
рассмотренных в гл. 7
расходомеров.
метода измерения
расхода:
1 — байпасная
трубка; 2 — расходомер; 3 —
пиафрагма, установленная в основном
трубо-проводе
31
Q
Если между
расходом Q в основном трубопроводе и
расходом q в байпасе существует
стабильная функциональная зависимость
Q = f(q), то по результатам измерения
q в каждом конкретном случае можно
определить Q. Для этого необходимо лишь
определить зависимость между Q и q
при непосредственной (в ограниченной
области) или расчетной градуировке
(например, по соотношению сопротивлений
основного и байпасного
трубопроводов).
Погрешность измерения
расхода парциальным методом будет
складываться из погрешностей установления
и стабильности зависимости Q=f(q) и
измерения расхода в байпасе.
Измерение
расхода методом гидравлического удара.
Гидравлический удар, возникающий при
быстром перекрытии потока капельной
жидкости (за счет инерционного воздействия
внезапно остановленной массы жидкости),
вызывает колебания давления в
трубопроводе, фронт которых
распространяется со скоростью звука.
Процесс изменения давления в сечении
трубопровода, находящемся на расстоянии
L перед перекрывающей поток задвижкой,
графически изображен на рис. 83, на
котором
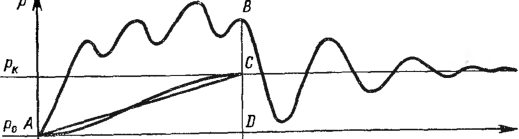
Рис.
83. График изменения давления в трубопроводе
при гидравлическом
ударе
Ро — начальное статическое
давление в контрольном сечении; рк
— конечное статическое давление в том же
сечении. Точка А соответствует началу
перекрытия потока задвижкой, точка В —
окончанию.. Затухающие колебания после
закрытия задвижки (по истечении времени ДО
характеризуют лишь инерционные свойства
прибора, примененного для записи изменений
давления.
Линия АС характеризует
изменение давления, связанное с изменением
гидравлического сопротивления задвижки
при перемещении ее затвора, а линия АВ —
изменение давления вследствие
гидравлического удара.
Закон количества
движения при гидравлическом ударе имеет
вид
At
pLQ = F f Apdt,
(7.48)
At 0
где /
Др dt — импульс ударной волны, равный
площади/д
диаграммы
О
изменения давления (см.
рис. 83), ограниченной линиями АВ и AC; F —
площадь сечения трубопровода.
Откуда
искомый объемный расход
Q = /д–
(7.49)
Таким образом,
планиметрируя диаграмму изменения
давления, измерив предварительно диаметр
трубопровода (а, следовательно, и F),
длину контрольного участка/, и плотность
протекающей среды, по выражению (7.49) можно
рассчитать объемный расход.
Данный
метод применяют при испытаниях
гидравлических машин и насосов, т. е. в тех
случаях, когда расход можно измерять после
воспроизведения (а не в процессе испытаний)
определенных режимов
испытаний.
Измерение расхода с помощью
интегрирующей трубки. Интегрирующая трубка
представляет собой цилиндрический зонд,
полностью пересекающий поток по диаметру
водовода. По образующей трубки просверлен
ряд отверстий для отбора давления
набегающего потока.
Статическая
характеристика интегрирующей трубки имеет
вид
Q = V<of ~ Др’ (7.50)
где
Др — перепад давлений, отбираемых в конце
интегрирующей трубки и со стенок водовода;
— коэффициент расхода трубки; со —
площадь сечения
отверстий.
Автомодельность
коэффициента расхода для трубок с
отношением толщины стенки к диаметру
отверстия, равным 0,33, наступает при числах
Рейнольдса, больших 106. Значение ip
при этом устойчиво стремится к единице.
‘
В этих условиях возможность расчетной
градуировки интегрирующих трубок
обусловливается соответствием величины
у/ — &р сред-
р
ней скорости
потока. ‘
Однако влияние температуры
измеряемой среды, пульсаций давления и
расхода, трудности технологического
порядка не позволяют на сегодняшний день
получить погрешности измерения расхода
интегрирующими трубками, меньшие 6—8 %.
Кроме того, область применения данных
устройств ограничивается измерением
расхода чистых однофазных
веществ.
Методы смешения. Принцип
измерений,^лежащий в основе зтих методов,
заключается в следующем. В протекающее по
трубопроводу вещество вводят раствор
реагента („прививку”) и определяют
кратность разбавления этого реагента в
потоке вещества.
Уравнение баланса
реагента, вводимого в поток, имеет
вид
qCt QC0 = (Q q)C2,
(7.51)
где q — расход раствора
реагента, вводимого в поток; С0,
Сt,C2 — концентрации реагента
соответственно в среде до „прививки” в
растворе реагента и в смеси, отбираемой из
потока после „прививки”.
В
соответствии с выражением (7.51) уравнение
измерений данным методом будет
сг-с0 с –
с
гдеК = —-– –коэффициент
разбавления.
Сг —
С0
Если в самом измеряемом
веществе не содержится примесей вводимого
реагента или они ничтожно (по сравнению с
С2) малы, то К = = CJC2 —
1.
Расход q может быть измерен с
достаточно высокой точностью, чего нельзя
сказать о точности измерения величины К
Действительно, если концентрация реагента
(С2) в отбираемом из потока пробе
ненамного превышает его концентрацию в
„чистой” среде (С0), а именно к
этому и стремятся при реализации метода, то
даже незначительные погрешности измерений
С2 и С0 приведут к
существенно недостоверной оценке величины
К.
Другой разновидностью методов
смешения является метод интегрирования,
заключающийся в том, что в поток вещества за
малый промежуток времени вводят
определенную объемную порцию V раствора
реагента и непрерывно (в течение времени
t) следят за изменением концентрации
С реагента в потоке.
Уравнение этого
метода, полученное на основе баланса
объемных количеств реагента, имеет
вид
Q = —f-. (7.53)
/
Cdt
с
Методы смешения используют в
настоящее время исключительно для
измерения расхода воды в цилиндрических
водоводах. В качестве реагентов в растворах
с концентрацией 10-4—10 мг/д применяют
дихромат натрия, хлорид натрия, родамин и
другие химически пассивные к воде вещества
(в основном, соли). Применяют и
радиоактивные „прививки”, например,
изотопы брома, натрия, йода. Использование
радиоактивных реагентов позволяет
осуществить бесконтактные измерения,
однако требует обеспечения специальных,
условий работы.
.. Основным источником
погрешности определения расхода методами
смешения является .неравномерность
распределения, концентрации вводимого
реагента по сечению, в котором отбирают
пробы. Относительная неравномерность
распределения концентрации, а
следовательно, и вызываемая ею погрешность,
зависит от расстояния Lc между
устройствами для ввода раствора реагента в
поток и отбора проб (расстояния смешения), а
также характеристик потока. Для
обеспечения приемлемых (меньших 1,5 %)
значений погрешности Lc должно
быть большим 6QD (.D — диаметр
трубопровода).
Предложено несколько
способов уменьшения неравномерности
распределения концентрации и сокращения-
Lc. Например, одновременное
впрыскивание, раствора реагента с помощью
ряда инжекторов, равномерно расположенных
на кольцевой линии, радиус которой
составляет 0,63 радиуса трубопровода;
искусственная турбулизация потока на
участке смешения с помощью различных
местных сопротивлений; отбор проб в
нескольких точках сечения потока и
определение осредненной концентрации.
Особенно эффективен последний
способ.
При соблюдении оптимальных
условий погрешность измерения расхода
методами смешения (без учета влияния
турбулентности, изменений температуры,
наличия примесей и т. п.), по-видимому, может
быть оценена в 1,5—2,5 % верхнего предела
измерений. Однако достоверных данных на
зтот счет до настоящего времени не
имеется.
Основным достоинством методов
смешения является отсутствие
необходимости определения площади сечения
трубопровода.
„Точечные” методы
основаны на измерении локальной скорости в
одной какой-либо точке потока и определении
расхода по теоретической или эмпирической
зависимости между измеренной локальной и
средней скоростями потока.
Локальную
(местную) скорость можно измерять
различными методами (оптическими,
акустическими, тепловыми) и приборами
(трубки скоростного напора, микровертушки,
термоанемометры, электромагнитные
измерители скорости и др.).
По существу,
если известна модель развитого
турбулентного потока, с достаточной
точностью описывающая распределение его
скоростей, то локальную скорость при
реализации „точечного” метода можно
измерять в любой фиксированной точке
потока. Однако отсутствие такой
(метрологически пригодной) модели
обусловило практическое использование на
сегодняшний день лишь двух модификаций
„точечного” метода — метода средней
скорости и метода максимальной
скорости.
К контрольному вопросу №
14
Вы неправильно ответили на
вопрос.
Разберитесь как следует в
физических принципах, лежащих в основе
ультразвуковых и ЯМР-расходомеров- Ведь
вполне возможно, что в своей практической
деятельности Вам придется столкнуться с
этими новыми достаточно универсальными
расхо-’ доизмерительными
устройствами.
Суть первого метода
заключается в измерении локальной скорости
в точке, где скорость равна средней
скорости потока. Тогда по результатам
предварительных измерений диаметра
трубопровода и показаниям измерителя
местной скорости (ИМС) можно определить
расход.
По уточненным данным А.Д.
Альтшуля ордината точки, где скорость равна
средней скорости развитого
осесиммегричного турбулентного
потока
г0 = 0,777/?,
(7.54)
где R — радиус
трубопровода в месте установки
ИМС.
Соотношение (7.54) и положено в основу
метода средней скорости.
Погрешности
измерений г0, установки ИМС,
изменение местоположения точки средней
скорости при изменении чисел Рейнольдса,
коэффициента гидравлического трения,
турбулентные пульсации — все это
обусловливает погрешность измерения
данным методом, равную 4—6 % верхнего
предела измерений.
Второй метод — метод
максимальной скорости заключается в
измерении скорости на оси трубопровода
(максимальной) и определении расхода по
уточненным соотношениям между
максимальной и средней скоростями
потока.
Достоинствами второго метода
являются: стабильность ординаты точки
(всегда жестко фиксирована на
геометрической оси осесимметричного
потока), в которой скорость максимальна;
независимость ординаты от чисел Рейнольдса
и характеристик потока; наибольшая
удаленность места установки ИМС от стенок
трубопровода, что существенно снижает
требования к его габаритным размерам. Так,
при установке ИМС в точке средней скорости
наибольшая площадь сечения ИМС не должна
превышать 0,01 площади сечения трубопровода,
при установке же ИМС на оси трубопровода
отношение площадей может быть увеличено до
0,06.
Использование наиболее
универсального соотношения между средней и
максимальной скоростями развитого
осесимметричного турбулентного потока
дает следующее рабочее уравнение измерений
расхода методом максимальной
скорости
Q = ttR2S (0,75 0,0275 lg -^-)
(7.55)
(S — показания ИМС,
установленного на оси трубопровода
радиусом/?) и позволяет оценить погрешность
метода в 3—5 % верхнего предела
измерений.
Суть кросс-корреляциоиного
метода заключается в определении функции
корреляции между случайными пульсациями
скорости в двух точках (А и В)
турбулентного потока, отстоящими друг от
друга на расстояние L.
Так как
функция корреляции случайных величин
характеризует степень их связи и степень их
взаимообусловленности во времени, то
очевидно, что максимум ее будет
соответствовать времени перемещения
турбулентных возмущений из точки А в
точку В (так как степень временной
взаимообусловленности тех же самых
пульсаций, естественно,
максимальна).
Полученный вывод
справедлив и для осредненных по сечению
потока пульсационных составляющих
скоростей.
Таким образом, зафиксировав
пульсационные составляющие скоростей в
двух сечениях потока, отстоящих друг от
друга на расстояние L, определив (с
помощью специального прибора —
коррелографа) функцию корреляции между
ними и измерив (автоматически или
непосредственно по рис. 84) значение времени
тт, соответствующее максимуму
(пику) этой функции фхут, можно
определить расход потока по формуле
Q =
F(7.56)
Тт
Сам метод
прост, однако его аппаратурная реализация,
требующая наличия ультразвуковых или
лазерных измерителей пульсационных
составляющих скоростей, коррелографа и
устройств автоматической регистрации
тт довольно сложна.
При
компенсации наиболее существенных
методических и аппаратурных погрешностей
точность метода соответствует приведенной
погрешности ±(2—2,5) % в диапазоне
значений измеряемых расходов 15:1.
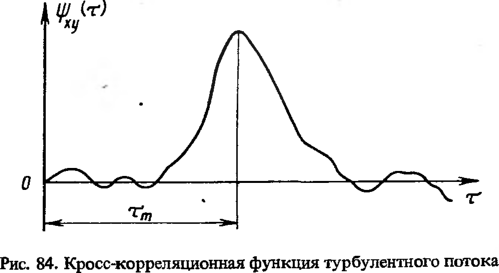
К
контрольному вопросу № 15
Сравните
уравнения измерений расходомеров,
описанных в гл. 2, и убедитесь, что
единственно пригодными для этих условий
измерений являются гироскопические или
кориолисовы расходомеры.
7.13. Измерение
расхода многофазных сред
В
расходоизмерительной практике довольно
часто встречаются задачи, связанные с
измерением расхода двух- или трехфазных
сред. К наибо-
лее типичным промышленным
средам относятся влажный пар, нефтегазовые
смеси, пульпы, пылеугольное топливо (смесь
воздуха с угольным порошком), водогрунтовые
смеси, низкокипящие криогенные вещества,
поток которых в отдельных случаях
представляет смесь жидкой, газообразной и
твердой (шуги) фаз.
Трудности
обеспечения приемлемой (в некоторых
случаях довольно высокой, характеризуемой
допускаемой погрешностью 2—3 %) точности
измерения расхода таких сред
обусловливаются множеством физических и
технических причин, главные из которых —
различие скоростей течения фаз через
первичные преобразователи применяемых
расходомеров (например, сужающие
устройства); неоднородность распределения
фаз по сечению потока; значительные
флуктуации скоростей, давлений и
концентраций фаз.
Основными параметрами
многофазных сред, определяющими
отличительные особенности их движения по
трубам и степень влияния указанных выше
причин на точность измерения расхода,
являются массовая концентрация фаз в
потоке и их плотность. Вследствие этого, как
правило, приходится измерять расход таких
сред в единицах массы (массовый расход) или
объемный расход и плотности, фаз, что также
вносит дополнительные технические
трудности.
Наличие значительных
флуктуаций параметров многофазных сред при
их течении по трубам и каналам затрудняет, а
в ряде случаев делает невозможным,
измерение мгновенных или осредненных за
малый промежуток времени значений расхода.
Так, при движении газожидкостных смесей по
трубам при некоторых концентрациях
(относительном содержании) жидкой и
газообразной фаз и определенных скоростях
поток смеси приобретает „пробковый”
характер (смесь движется в ввде
последовательных „пробок” жидкости и
газа, занимающих все сечение трубопровода,
— то только жидкость, то только газ).
Естественно, при этом понятие мгновенного
расхода смеси теряет смысл.
Вследствие
отмеченного на практике в большинстве
случаев измеряют средний (осредненный за
достаточно большой промежуток времени — не
менее 40—60 с) расход многофазных
потоков.
Среди множества измерительных
задач, возникающих в практике измерения
расхода многофазных сред, можно выделить
две наиболее типичные:
1)
измерение общего (суммарного)
расхода среды (смеси);
2)
измерение расхода отдельных
компонентов (фаз) смеси, например, сухой
части влажного пара или твердой фазы во
взвесенесущем потоке.
Каждая из этих
задач решается своими специфическими
техническими способами и приемами.
Так,
для измерения общего (суммарного) расхода
Мс диспергированных двухфазных
сред (сухой пар влага; воздух угольная
пыль и
т. п.) наиболее распространены
расходомерыссужающимиустройствами.
Как
показали результаты теоретических и
экспериментальных исследований, рабочая
формула измерений при этом (связь между
расходом и перепадом давлений Др на
сужающем устройстве) имеет вид
Данная
формула отличается от рассмотренных ранее
уравнений метода переменного перепада
давлений тем, что в нее входит коэффициент
/3, зависящий в общем случае от массовой
концентрации 77 тяжелой фазы (массовой доли
тяжелой фазы в смеси), плотностей легкой
рл и тяжелой рт фаз, геометрии
сужающего устройства и скоростей течения
фаз в приемном преобразователе. Кроме того,
сомножителем перед Ар в данную формулу
входит плотность смеси
Рс =
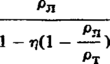
(7.58)
Если
скорости легкой и тяжелой фаз при течении
смеси через приемный преобразователь
несущественно отличаются друг от друга (что
характерно, например, для стандартных
диафрагм, у которых участок сужения при
достаточно больших т очень короткий и
вследствие этого частицы тяжелой фазы на
этом участке почти не ускоряются), то в
ограниченной области значений rj (77
< 0,2 — для влажного пара: V < 0,35 —
для смеси воздуха с угольным порошком)
коэффициент
1
(7.59)
V
1 — 7}
Во многих случаях отношение
рл/рт много меньше 1. Так,для
влажного пара рл/рх = 0,001—0,005;
для пылеугольного топлива это отношение
еще меньше.
Тогда на основании формулы
(7.58)
![]()
(7.60)
и
уравнение измерений (7.57) с учетом выражений
(7.59), (7.60) преобразуется к виду
ЛГС(1
– v) = aeFo V 2рлДр ‘.
(7.61)
Как следует из зтой формулы,
перепад давлений на диафрагме (при
сделанных допущениях и в ограниченной
области значений т?) характеризует лишь
массовый расход Мл = Мс (1
— 7j) легкой фазы. Этот вывод, подтвержденный
экспериментально, объясняется тем, что при
принятом равенстве скоростей легкой и
тяжелой фаз энергия на ускорение тяжелой
фазы не затрачивается.
Таким образом,
при использовании стандартной диафрагмы
расход легкой фазы (сухой части влажного
пара или воздуха для пылеугольного топлива)
может быть определен по
уравнению
М„ = aeFо V 2рлДрд
,
(7.62)
где Дрд —
измеренный перепад давлений при течении
смеси; коэффициент расхода а
принимается равным табличному
значению.
При известной массовой
концентрации тяжелой фазы г) полный
расход смеси вычисляют по формуле
”
.?/ ‘.-in—i.
г..-.,
л/с = —* .. М
(7.63)
‘г-‘ЖК Я – •
4
расход тяжелой
фазы
. V —- Mr =Mcv=млуЛ¦— . (7.64)
В случае,
если г] неизвестна или изменяется в
процессе измерений, приходится определять
ее по результатам измерения перепада
давлений на дополнительно устанавливаемых
в поток смеси трубе или сопле Вентури –
Арв. Отношение (или разность)
Арв и Дрд характеризует
часть энергии потока, затрачиваемой на
ускорение твердой фазы при течении смеси
через трубу или сопло Вентури (напомним, что
при течении смеси через диафрагму
ускорение твердой фазы практически не
наблюдается) . Следовательно, данное
отношение будет пропорционально
содержанию твердой фазы 7?.
Для расчетов
17 используют
экспериментально-апробированную
зависимость
73
Арп
^ 775″ =
д ^Г ~ ¦ <765>
где
р0 — коэффициент, зависящий от
свойств твердой фазы и геометрии
применяемых сужающих устройств и
определяемый путем опытной градуировки
комплекта расходомёров.
Тогда в
соответствии с формулой (7.65)
’’“-тЬг-
(7–66)
где А =
Дрв/Лра.
Таким образом,
при измерениях расхода методом переменного
перепада давлений двухфазных сред с
неизвестной массовой концентрацией
твердой фазы измеряют перепады давлений на
двух последовательно установленных
сужающих устройствах (диафрагме и сопле или
трубе Вентури), по формулам (7.61) и (7.66)
рассчитывают расход легкой фазы и
Т],а затем по формулам (7.63) и (7.64) –
общий расход смеси и расход твердой фазы.
Расчетные операции при этом могут
выполняться вычислительными устройствами,
сблокированными со вторичными
преобразователями расходомеров.
Еще раз
подчеркнем, что все изложенное справедливо
для хорошо диспергированных двухфазных
штоков с равномерной концентрацией фаз и в
ограниченной области значений
7].
Расходомеры переменного перепада
давлений довольно часто применяют и для
измерения расхода различных пульп и
водогрунтовых смесей. Характерной
особенностью данных сред является то, что
плотности их легкой и тяжелой фаз мало
отличаются друг от друга. В этом случае
суммарный расход смеси определяют по
уравнению (7.57), в котором коэффициент Р
принимают равным единице.
Расход смесей
твердой и жидкой (или газообразной) фаз
измеряют комбинированными методами,
основанными на определении общего
объемного расхода смеси и содержания в ней
твердой фазы. Объемный расход смеси
измеряют при этом с помощью
электромагнитных, ультразвуковых,
ядерно-магнитных и расходомеров других
типов, приемные преобразователи которых не
имеют выступающих внутрь потока элементов.
Расходомеры устанавливают на вертикальных
участках трубопровода для предотвращения
скапливания более тяжелой фазы в нижней
части сечения трубы.
Содержание твердой
фазы определяют по показаниям
радиоизотоп-ных концентратомеров,
радиоактивных или компенсационных весовых
плотномеров. Наибольшее применение находят
весовые плотномеры, представляющие собой
участок трубопровода с гибкими
сочленениями, подвешенный на ленточных
опорах. При изменении массы смеси,
протекающей по данному участку, он
перемещается в вертикальном направлении
вместе с плунжером индуктивной катушки.
Перемещение плунжера вызывает сигнал
рассогласования, приводящий во вращение
электродвигатель. При этом изменяется
натяжение уравновешивающей пружины, что
возвращает участок в исходное положение.
Угол поворота электродвигателя,
фиксируемый ферродинамическими
преобразователями, является мерой
плотности протекающего
вещества.
Компенсационные весовые
плотномеры в комплекте с электромагнитными
расходомерами получили преимущественное
применение для измерения расхода твердого
топлива (угля, торфа) при его
гидротранспорте.
Расход пульп, сыпучих
материалов, нефтегазовых смесей измеряют и
массовыми расходомерами, в основном —
кориолисовыми. Предпочтительное
применение этих расходомеров объясняется
тем, что измеряемая среда в приемном
преобразователе кориолисовых расходомеров
(см. рис. 78) движется перпендикулярно к оси
вращения потока и вследствие этого
„кориолисовы” усилие и момент не зависят
от распределения фаз.
В заключение
отметим, что совершенствование техники
измерений расхода многофазных сред
сдерживается отсутствием высокоточных
образцовых стендов и установок, способных
воспроизводить все характерные
особенности течения таких сред (структуру
потока, геометрию и распределение фаз). И
хотя кое-какие сдвиги в этой области
определенно наметились, работы здесь
„непочатый край”.
Одной из
перспективных отечественных разработок,
восполняющих этот пробел, является
созданная во Всесоюзном
научно-исследовательском институте
расходометрии (ВНИИР) исходная образцовая
установка, реализующая принцип смешения
потоков жидкости и газа для
воспроизведения и измерения параметров
газожидкостных потоков (рис. 85). Установка
работает следующим образом. Жидкость (вода)
из резервуара 10 насосом 13 через
систему стабилизации напора, состоящую из
бака 8,
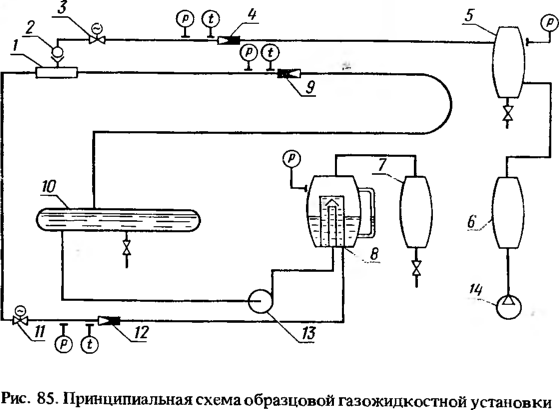
где
поддерживается постоянный уровень
жидкости, и воздушного ресивера 7, подается
в смеситель 1. Расход жидкости
регулируется задвижкой 11 и измеряется
турбинным расходомером 12. Одновременно
с этим компрессором 14 через ресивер
6, узел стабилизации расхода 5 и эжектор 2
в смеситель подается воздух. Расход воздуха
регулируется задвижкой 3 и измеряется
турбинным расходомером 4. Из смесителя
газожидкостная смесь подается в
испытательный участок, на котором
устанавливается градуируемый или
поверяемый расходомер 9, и затем
сбрасывается в резервуар 10, где она
сепарируется (разделяется на газ и
жидкость). Давление и температуру смеси
контролируют при помощи измерительных
преобразователей, обозначенных на
схемер и t соответственно.
Кроме
того, для измерения действительной
расходной концентрации и идентификации
различных режимов течения смеси
(дисперсного, разделенного, пробкового)
установка снабжена емкостным измерителем
ее диэлектрической
проницаемости.
Метрологические
исследования и аттестация установки
показали, что осуществляя рассмотренный
принцип смешения и используя для
раздельных измерений расхода жидкости и
газа индивидуально аттестованные
турбинные расходомеры, возможно обеспечить
воспроизведение и измерение расхода
газожидкостных потоков с погрешностью, не
превышающей 0,8—1,0%.
7.14.
Измерение переменных расходов
В
практике измерения переменных расходов
приходится иметь дело с двумя наиболее
типичными измерительными
задачами:
измерение мгновенного
значения расхода, что характерно, для
систем автоматического регулирования
технологическими процессами, управления
работой энергетических установок или
измерений в условиях существенного
систематического „тренда” (монотонного
возрастания или уменьшения)
расхода;
измерение среднего
(осредненного за достаточно большой
промежуток времени) расхода, что характерно
для систем учета или измерений
пульсирующих относительно какого-либо
среднего значения
расходов.
Качественное (обеспечивающее
приемлемую точность измерений) решение
каждой из этих задач достигается
правильным выбором динамических
характеристик применяемых расходомеров
или умением оценить дополнительную
динамическую погрешность при известных
динамических характеристиках
расходомеров.
Наиболее полно
динамические свойства любой измерительной
системы (ее инерционность, обусловливающую
запаздывание и искажение выходного сигнала
относительно входного) описываются
переходной характеристикой — зависимостью
выходного сигнала от изменяющегося во
времени входного при заданных параметрах
измерительной системы.
В
расходоизмерительной практике наиболее
часто приходится иметь дело с двумя
классами приборов, отличающихся видом
переходной характеристики, а
следовательно, и обобщенными динамическими
свойствами. К первому классу относятся
расходомеры, представляющие собой
инерционное звено первого порядка,
переходная характеристика которых
описывается линейным дифференциальным
уравнением первой степени
T^- y = Q{t),
(7.67)
где у — выходной
сигнал (показания) расходомера, выраженный
в единицах входного сигнала (расхода) Q(t);
Т — постоянная времени расходомера,
с.
Величина Т характеризует
инерционное запаздывание выходного
сигнала и определяется следующим образом.
Если на вход прибора подать скачкообразный
импульс расхода LQ, то в соответствии с
переходной характеристикой (7.67) изменение
выходного сигнала Лу будет описываться
уравнением
Ay = AQ(l (7.68)
Из
этого уравнения следует, что полное
соответствие выходного сигнала
действительному значению расхода (при
ТФО) наступит лишь при t = °о, т. е. в
связи с инерционностью расходомера
переходный процесс (процесс установления
действительного значения выходного
сигнала) длится бесконечно долго.
При
t = Т, как следует из формулы (7.68),
Дут = 0,632Дб- Следовательно, постоянная
времени Т соответствует времени, в
течение которого изменение выходного
сигнала достигает значения 0,632 от полного
скачкообразного импульса входного
сигнала.
Напомним еще раз, что значения
выходного сигнала при этом должны быть
выражены (через коэффициент преобразования
или по именованной шкале) в единицах
входного.
К расходомерам, переходная
характеристика которых описывается
линейным дифференциальным уравнением
первой степени вида (7.67), относят, например,
турбинные, тепловые и гидродинамические.
Естественно, такое „отнесение” носит
приближенный характер, однако существенно
облегчает практические расчеты
динамических погрешностей
расходомеров.
Так, решение уравнения (7.67)
для случая изменяющегося с постоянной
скоростью а расхода (Q = at)
имеет вид
y — a(t-T)
аТе,/т.
П.69)
Следовательно,
абсолютная динамическая погрешность
измерения расхода в этом случае
АУ =у-at
= аТ(ё~*’т – 1), (7.70)
а
максимальное ее значение
3
АУтах йТ.
Решение
уравнения (7.67) для случая пульсирующего
(относительно среднего значения
Qcp) с амплитудой В и частотой
со расхода (Q = Qcp Bsincot) имеет
вид
У — бср РУ sin(atf е),
(7.71)
I
где у =-
– —; е = arctg —
cot.
у/ О)2Т2
1
Следовательно, относительная
динамическая погрешность измерения
мгновенных значений пульсирующего расхода
приборами, представляющими собой
инерционное звено первого порядка
6 „
=-—- [7 sin (cot е) — sin o;f].
(7.72)
2(??ср В
sinuO
Максимальное значение этой
погрешности
5„ «
В–—- .
(7.73)
J шах о/п ,—-—
-’«
^ со2
7 2
1
И наконец, на основании
формулы (7.71) относительная динамическая
погрешность измерения средних (осредненных
за время Т0) значений
пульсирующего расхода
ВТ
cj7’(l-cosu>7’0) sinu>7’0
(ППЛЛ
ьу–^’~Тв‘
1 ‘
Формулы (7.70), (7.73)
и (7.74) позволяют определить расчетное
значение постоянной времени Т по
заданным допускаемым значениям
динамических погрешностей (при известных
а, В, юл. Qcp) или оценить
эти
погрешности при известных расчетно или
экспериментально определенных) значениях
Г. ‘
Величина Т зависит от
характеристик (массы, геометрических
размеров, моментов инерции и других)
подвижных элементов и линий связи
измерительных преобразователей
расходомеров.
Так, для турбинных
расходомеров с аксиальным ротором
постоянная времени определяется
выражением
Г=~(р’^ р),
(7.75)
pQ /ж
где I
— длина лопасти ротора; S — площадь
живого сечения потока в зоне ротора; р, р
— плотности измеряемой среды и
материала ротора соответственно;
Jp, /ж — моменты инерции
плоского сечения ротора и сечения,
заполненного жидкостью,
соответственно.
Как следуёт из формулы
(7.75), в общем случае Т зависит не только
от конструктивных параметров
измерительных преобразователей, но и от
значений входного сигнала
Q.
Переходная характеристика
расходомеров второго класса (к которым
относят расходомеры переменного и
постоянного перепада давлений) описывается
линейным дифференциальным уравнением
второго порядка
Т1 T3^r y =
Q{f), (7.76)
где Тс
характеризует время или круговой период
свободных колебаний подвижной системы
прибора, а постоянная времени Т3 —
время запаздывания прибора.
Отношение (3
– TJ2TC называется степенью
успокоения или демпфирования
прибора.
Выводы, аналогичные
приведенным выше (для инерционных звеньев
первого порядка), дают следующие выражения
для оценки относительных динамических
погрешностей расходомеров данного
класса:
5′ = -^3_(e-w_l),
(7.77)
Т /
т2 – тг 1
^
где Ъ — — -^-5—_ _ лрИ
измерении мгновенных значений
мо-
2ГС
нотонно изменяющегося с
постоянной скоростью а расхода;
О.
(7-78)
где а =
1 –‘при
измерении мгновенных значе-
/ (1 – bSTlf
4/3347и? Т?
ний пульсирующего с амплитудой В и
частотой со расхода;
– -4dlb
20:toTc
.VOIW ¦”
где e =
arctg–—-—- – при измерении осредненрых
за.нремя Т0
–_
С
значений пульсирующего
расхода. ^
Как следует из
приведенных формул, динамические
погрешности расходомеров при известном
виде переходной характеристики целиком
определяются их постоянными времени (Т
— для линейных переходных характеристик
первого порядка, Тс и Т3
— для линейных переходных характеристик
второго порядка). Чем меньше Т; Тс
и Т3, тем лучше инерционные
свойства прибора и тем меньше динамические
погрешности измерения параметров
переменных расходов. Обычно Тс в
3—4 раза меньше постоянной времени
запаздывания Т3 (Т), которая у
турбинных и тепловых расходомеров
составляет 0,005—0,1 с, у ротаметров — 0,5—3 с (в
зависимости от массы поплавка,
геометрических параметров поплавка и
трубки), у электромагнитных и
ультразвуковых расходомеров — 0,0001—0,001 с, у
расходомеров с сужающими устройствами (в
зависимости от типа и конструктивных
особенностей используемых дифмано-метров,
длин и диаметров соединительных трубок,
плотности заполняющих систему
дифманометров жидкостей) — 0,5—10
с.
Следовательно, расходомеры
переменного перепада давлений в общем
случае являются наиболее (среди других
типов расходомеров) инерционными приборами
и наименее пригодны для измерения
параметров переменных расходов. Данное
обстоятельство усугубляется й наличием у
этих расходомеров дополнительной
динамической погрешности, обусловленной
квадратичной зависимостью расхода и
перепада давлений. Действительно,
квадратный корень из измеренного
дифманометром среднего перепада давлений
больше среднего значения корня из перепада,
характеризующего осредненный за время
Т0 расход, т. е.
у/ -4г~ i°(Pi
-Pi) dt>-±- Л/ (Pi -р2) dt.
1 Q О
-* о
0
Вследствие этого при
измерении средних значений пульсирующего с
амплитудой Врасхода будет
возникать дополнительная погрешность
/-
= (V 1
—2-г- О * Ю0%. (7.80)
¦
2бср
И тем не менее в практике довольно
часто встречаются случаи измерения
пульсирующих расходов расходомерами
переменного перепада давлений. Наилучшим
способом уменьшения существенных
динамических погрешностей при этом
является сглаживание пульсаций
специальными фильтрами-успокоителями.
Отметим, что этот способ пригоден и для
уменьшения динамических погрешностей
расходомеров любых типов. Пульсация
сглаживается тем сильнее, чем больше объем
системы V (включая и емкость
фильтра-успокоителя) между источником
пульсаций и сужающим устройством и чем
больше падение давления на этом участке,
соответствующее среднему расходу
Qcp.
Для оценки сглаживающего
эффекта служит безразмерный критерий
успокоения пульсаций, предложенный П.П.
Кремлевским
к = —
Y“AP. (7.81)
te
всрРср
или К –
4пк,
где 26 — показатель
адиабаты измеряемой среды (в случае
измерения пульсирующих расходов газов или
пара).
Необходимая величина к (или
К), обеспечивающая приемлемые значения
динамических погрешностей расходомеров
переменного перепада давлений, зависит рт
характера пульсаций. Для одноцилиндровых
гидравлических машин характер пульсаций
определяется коэффициентом подачи S,
равным отношению времени т5
движения потока за один период ко времени
то полного периода, т. е. S —
т$/т0.
Для многоцилиндровых
гидравлических машин коэффициент
неравномерности расхода © равен отношению
минимального мгновенного расхода бткг к
максимальному мгновенному расходу
Qmax.
Таблицы и номограммы для определения сопротивления
изоляции по величинам затухания сигнала для частот f = 3,1
гц и f = 1000 гц.
(Таблицы и графики на частоты F = 1,5; 6,25; 12,5; 175; 450; 512; 640; 1425; 8200 и 10000 Гц
высылаются по запросам пользователей)
Таблица определения величин
сопротивления покрытия по величинам затухания сигнала частотой 3,1 Гц для
трубопроводов диаметром 159 ¸ 530 мм
Затухание, мБ | Сопротивление | ||||||
D =159 мм | D =219 мм | D =273 мм | D =325 мм | D =377 мм | D =425 мм | D =530 мм | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0,0102 | 100000 | – | – | – | – | – | – |
0,0113 | – | 100000 | – | – | – | – | – |
0,0118 | – | – | 100000 | – | – | – | – |
0,0125 | – | – | – | 100000 | – | – | – |
0,0131 | – | – | – | – | 100000 | – | – |
0,0136 | – | – | – | – | – | 100000 | – |
0,015 | – | – | – | – | – | – | 100000 |
0,0159 | – | – | – | – | – | – | – |
0,0175 | – | – | – | – | – | – | – |
0,0186 | – | – | – | – | – | – | – |
0,02 | – | – | – | – | – | – | – |
0,0213 | – | – | – | – | – | – | – |
0,0243 | – | – | – | – | – | – | – |
0,0268 | – | – | – | – | – | – | |
0,0394 | 10000 | – | – | – | – | – | – |
0,0438 | – | 10000 | – | – | – | – | – |
0,0462 | – | – | 10000 | – | – | – | – |
0,0486 | – | – | – | 10000 | – | – | – |
0,0504 | – | – | – | – | 10000 | – | – |
0,0518 | – | – | – | – | – | 10000 | – |
0,0578 | – | – | – | – | – | – | 10000 |
0,0621 | – | – | – | – | – | – | – |
0,0678 | – | – | – | – | – | – | – |
0,0723 | – | – | – | – | – | – | – |
0,0778 | – | – | – | – | – | – | – |
0,0825 | – | – | – | – | – | – | – |
0,0945 | – | – | – | – | – | – | – |
0,104 | – | – | – | – | – | – | |
0,151 | 1000 | – | – | – | – | – | – |
0,16 | 920 | – | – | – | – | – | – |
0,168 | – | 1000 | – | – | – | – | – |
0,17 | 830 | 990 | – | – | – | – | – |
0,177 | – | – | 1000 | – | – | – | – |
0,18 | 750 | 895 | 980 | – | – | – | – |
0,186 | – | – | 1000 | – | – | – | |
0,19 | 680 | 810 | 890 | 980 | – | – | – |
0,194 | – | – | – | – | 1000 | – | – |
0,2 | 625 | 750 | 810 | 900 | 960 | – | – |
0,204 | – | – | – | – | – | 1000 | – |
0,22 | 530 | 640 | 695 | 770 | 810 | 880 | – |
0,223 | – | – | – | – | – | – | 1000 |
0,239 | – | – | – | – | – | – | – |
0,25 | 427 | 510 | 560 | 610 | 650 | 705 | 820 |
0,259 | – | – | – | – | – | – | – |
0,27 | 375 | 450 | 480 | 540 | 575 | 620 | 720 |
0,276 | – | – | – | – | – | – | – |
0,299 | – | – | – | – | – | – | – |
0,3 | 312 | 373 | 408 | 450 | 470 | 520 | 600 |
0,315 | – | – | – | – | – | – | – |
0,32 | 280 | 337 | 366 | 410 | 430 | 467 | 540 |
0,35 | 240 | 290 | 315 | 350 | 370 | 400 | 465 |
0,362 | – | – | – | – | – | – | – |
0,37 | 218 | 263 | 286 | 315 | 336 | 365 | 425 |
0,4 | 192 | 230 | 250 | 275 | 295 | 318 | 370 |
0,42 | 185 | 211 | 231 | 255 | 270 | 295 | 340 |
0,45 | 158 | 188 | 203 | 226 | 249 | 259 | 300 |
0,47 | 145 | 175 | 190 | 208 | 222 | 242 | 278 |
0,5 | 132 | 158 | 173 | 188 | 200 | 218 | 249 |
0,54 | 117 | 138 | 150 | 167 | 175 | 192 | 218 |
0,6 | 97 | 117 | 127 | 140 | 148 | 160 | 184 |
0,64 | 89 | 105 | 115 | 126 | 133 | 144 | 164 |
0,7 | 78,5 | 82 | 98 | ПО | 115 | 124 | 142 |
0,74 | 72 | 84 | 91 | 100 | 105 | 114 | 129 |
0,8 | 65 | 75 | 81 | 89 | 94 | 100 | 114 |
0,84 | 60 | 70 | 76 | 83 | 87 | 93 | 105 |
0,9 | 54,5 | 63,5 | 68,5 | 75 | 78 | 84 | 95 |
0,94 | 51,5 | 59,5 | 64 | 70 | 73,5 | 79 | 88,5 |
1 | 47,5 | 54,5 | 58,5 | 64 | 67,5 | 72 | 80,5 |
1,1 | 41,5 | 48 | 51,5 | 56 | 59 | 62,5 | 70 |
1,2 | 37,3 | 42,6 | 45,8 | 49,8 | 52,5 | 55,5 | 62 |
1,3 | 33,5 | 38,3 | 41 | 44,5 | 46,8 | 49,5 | 55,5 |
1,4 | 30,5 | 35 | 37,5 | 40,5 | 42,5 | 45 | 50 |
1,5 | 28 | 32 | 34 | 36,8 | 38,5 | 40,8 | 45 |
1,6 | 26 | 29,9 | 31,5 | 34 | 35,8 | 37,8 | 42 |
1,7 | 24 | 27,3 | 29 | 31,3 | 32,8 | 34,5 | 38,3 |
1,8 | 22,5 | 25,5 | 27 | 29,5 | 30,5 | 32,3 | 35,7 |
1,9 | 21,1 | 23,8 | 25,3 | 27,3 | 28,5 | 29,9 | 33 |
2 | 19,8 | 22,4 | 23,8 | 25,5 | 26,9 | 28,1 | 31 |
2,5 | 15,5 | 17,4 | 18,5 | 19,8 | 20,7 | 21,6 | 23,7 |
3 | 12,9 | 14,3 | 15,2 | 16,2 | 16,8 | 17,6 | 19,2 |
3,5 | 11,2 | 12,3 | 13 | 13,8 | 14,3 | 14,9 | 16,2 |
4 | 9,9 | 10,7 | 11,3 | 12 | 12,5 | 13 | 13,9 |
4,5 | 8,9 | 9,7 | 10,2 | 10,8 | 11,2 | 11,6 | 12,4 |
5 | 8,2 | 8,9 | 9,3 | 9,8 | 10,1 | 10,4 | 11,3 |
6 | 7,2 | 7,7 | 8 | 8,4 | 8,7 | 8,9 | 9,5 |
7 | 6,5 | 6,9 | 7,2 | 7,5 | 7,7 | 7,9 | 8,4 |
8 | 6,1 | 6,4 | 6,6 | 6,8 | 7 | 7,2 | 7,5 |
9 | 5,7 | 6 | 6,2 | 6,4 | 6,5 | 6,6 | 6,9 |
10 | 5,5 | 5,7 | 5,9 | 6 | 6,2 | 6,3 | 6,5 |
12 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 | 5,7 | 5,9 |
14 | 5 | 5,1 | 5,2 | 5,2 | 5,3 | 5,4 | 5,5 |
16 | – | 5 | 5 | 5 | 5,1 | 5,2 | 5,3 |
18 | – | – | – | – | – | 5 | 5,1 |
20 | – | – | – | – | – | – | 5 |
25 | – | – | – | – | – | – | – |
30 | – | – | – | – | – | – | – |
35 | – | – | – | – | – | – | – |
Таблица определения величин сопротивления покрытия по величинам
затухания сигнала частотой 3,1 Гц для трубопроводов диаметром 620 ¸ 1420 мм
Затухание, мБ | Сопротивление | ||||||
D =620 мм | D =720 мм | D =820 мм | D =920 мм | D = 1020 мм | D = 1220 мм | D =1420 мм | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0,0159 | 100000 | – | – | – | – | – | – |
0,0175 | – | 100000 | – | – | – | – | – |
0,0186 | – | – | 100000 | – | – | – | – |
0,02 | – | – | – | 100000 | – | – | – |
0,0213 | – | – | – | – | 100000 | – | – |
0,0243 | – | – | – | – | – | 100000 | – |
0,0268 | – | – | – | – | – | – | 100000 |
0,0394 | – | – | – | – | – | – | – |
0,0438 | – | – | – | – | – | – | |
0,0462 | – | – | – | – | – | – | – |
0,0486 | – | – | – | – | – | – | – |
0,0504 | – | – | – | – | – | – | – |
0,0518 | – | – | – | – | – | – | – |
0,0578 | – | – | – | – | – | – | – |
0,0621 | 10000 | – | – | – | – | – | – |
0,0678 | – | 10000 | – | – | – | – | – |
0,0723 | – | – | 10000 | – | – | – | – |
0,0778 | – | – | – | 10000 | – | – | – |
0,0825 | – | – | – | – | 10000 | – | – |
0,0945 | – | – | – | – | – | 10000 | – |
0,104 | – | – | – | – | – | – | 10000 |
0,151 | – | – | – | – | – | – | – |
0,16 | – | – | – | – | – | – | – |
0,168 | – | – | – | – | – | – | – |
0,17 | – | – | – | – | – | – | – |
0,177 | – | – | – | – | – | – | – |
0,18 | – | – | – | – | – | – | – |
0,186 | – | – | – | – | – | – | – |
0,19 | – | – | – | – | – | – | – |
0,194 | – | – | – | – | – | – | – |
0,2 | – | – | – | – | – | – | – |
0,204 | – | – | – | – | – | – | – |
0,22 | – | – | – | – | – | – | – |
0,223 | – | – | – | – | – | – | – |
0,239 | 1000 | – | – | – | – | – | – |
0,25 | 920 | – | – | – | – | – | – |
0,259 | – | 1000 | – | – | – | – | – |
0,27 | 810 | 940 | – | – | – | – | – |
0,276 | – | – | 1000 | – | – | – | – |
0,299 | – | – | – | 1000 | – | – | – |
0,3 | 685 | 780 | 870 | 995 | – | – | – |
0,315 | – | – | – | – | 1000 | – | – |
0,32 | 610 | 705 | 780 | 890 | 970 | – | – |
0,35 | 525 | 605 | 670 | 770 | 835 | – | – |
0,362 | – | – | – | – | – | 1000 | – |
0,37 | 475 | 550 | 610 | 700 | 760 | 975 | – |
0,4 | 418 | 485 | 535 | 610 | 665 | 850 | 1000 |
0,42 | 370 | 445 | 495 | 565 | 615 | 790 | 920 |
0,45 | 340 | 392 | 435 | 500 | 542 | 695 | 820 |
0,47 | 315 | 365 | 405 | 464 | 505 | 645 | 760 |
0,5 | 285 | 330 | 364 | 415 | 455 | 580 | 685 |
0,54 | 249 | 285 | 320 | 363 | 398 | 510 | 600 |
0,6 | 208 | 240 | 267 | 305 | 334 | 428 | 503 |
0,64 | 188 | 215 | 239 | 272 | 298 | 380 | 450 |
0,7 | 162 | 185 | 205 | 234 | 257 | 327 | 386 |
0,74 | 146 | 168 | 187 | 212 | 233 | 297 | 351 |
0,8 | 128 | 147 | 163 | 186 | 203 | 258 | 307 |
0,84 | 118 | 136 | 152 | 173 | 187 | 240 | 284 |
0,9 | 107 | 120 | 134 | 153 | 167 | 212 | 250 |
0,94 | 99,5 | 113 | 125 | 143 | 156 | 197 | 234 |
1 | 90 | 102 | 113 | 128 | 141 | 178 | 212 |
1,1 | 78,5 | 88 | 97,5 | 112 | 120 | 152 | 180 |
1,2 | 69,5 | 77 | 85 | 96,5 | 105 | 133 | 156 |
1,3 | 61 | 68 | 75 | 85 | 92 | 115 | 135 |
1,4 | 55,5 | 61 | 68 | 76 | 83 | 102 | 119 |
1,5 | 50 | 55 | 61 | 68 | 74 | 91 | 106 |
1,6 | 46 | 50,5 | 55,5 | 62 | 68 | 83 | 97 |
1,7 | 42,3 | 46,2 | 50,5 | 57 | 61,5 | 75,5 | 87,5 |
1,8 | 39,4 | 43 | 47 | 53 | 57 | 70 | 80,5 |
1,9 | 36,4 | 40 | 43,5 | 48,5 | 52,5 | 64 | 74 |
2 | 34 | 37 | 40,5 | 45 | 49 | 59,5 | 68,5 |
2,5 | 25,8 | 27,8 | 30 | 33,6 | 36,5 | 43,7 | 49,7 |
3 | 20,8 | 22,2 | 24,1 | 26,7 | 28,7 | 34,1 | 38,7 |
3,5 | 17,5 | 18,7 | 20,2 | 22,3 | 23,9 | 28 | 31,8 |
4 | 15 | 16 | 17,3 | 18,8 | 20,3 | 23,8 | 26,7 |
4,5 | 13,4 | 14 | 15 | 16,6 | 17,8 | 20,4 | 23,1 |
5 | 12 | 12,7 | 13,6 | 14,7 | 15,8 | 18,3 | 20,4 |
6 | 10 | 10,6 | 11,3 | 12,3 | 13 | 14,8 | 16,2 |
7 | 8,8 | 9,2 | 9,7 | 10,5 | 11,2 | 12,7 | 14 |
8 | 7,9 | 8,2 | 8,7 | 9,3 | 9,9 | 11,1 | 12,2 |
9 | 7,3 | 7,5 | 7,9 | 8,5 | 8,9 | 9,9 | 10,8 |
10 | 6,8 | 7 | 7,3 | 7,8 | 8,2 | 9,1 | 9,8 |
12 | 6,1 | 6,3 | 6,5 | 6,9 | 7,2 | 7,8 | 8,4 |
14 | 5,7 | 5,8 | 6 | 6,3 | 6,5 | 7 | 7,5 |
16 | 5,4 | 5,5 | 5,6 | 5,8 | 6 | 6,5 | 6,8 |
18 | 5,2 | 5,3 | 5,4 | 5,6 | 5,7 | 6,1 | 6,4 |
20 | 5 | 5,1 | 5,2 | 5,4 | 5,5 | 5,8 | 6 |
25 | – | 5 | 5 | 5,1 | 5,2 | 5,3 | 5,4 |
30 | – | – | – | 5 | 5 | 5,1 | 5,2 |
35 | – | – | – | – | – | 5 | 5 |
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 159
мм и DT =
620 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 219
мм и DT =
720 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 273
мм и DT =
820 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 325
мм и DT =
920 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 327
мм и DT =
1020 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 425
мм и DT =
1220 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 3,1 Гц
для DT = 530
мм и DT=1420 мм
Таблица определения величин сопротивления покрытия по величинам
затухания сигнала частотой 1000 Гц для трубопроводов диаметром 159 ¸530
мм
Затухание, мБ | Сопротивление | ||||||
D =159 мм | D =219 мм | D =273 мм | D =325 мм | D =377 мм | D =425 мм | D =530 мм | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0,068 | 100000 | – | – | – | – | – | – |
0,07 | 92000 | – | – | – | – | – | – |
0,08 | 62000 | – | – | – | – | – | – |
0,084 | – | 100000 | – | – | – | – | – |
0,09 | 43000 | 81000 | – | – | – | – | – |
0,1 | 32000 | 59000 | 100000 | – | – | – | – |
0,11 | 24000 | 45000 | 76000 | – | – | – | – |
0,12 | 18500 | 35000 | 60000 | – | – | – | – |
0,122 | – | – | – | 100000 | – | – | – |
0,13 | 14500 | 27000 | 47000 | 82000 | – | – | – |
0,14 | 11700 | 22000 | 38000 | 63000 | – | – | – |
0,142 | – | – | – | – | 100000 | – | – |
0,15 | 9400 | 17500 | 31000 | 54000 | 84000 | – | – |
0,16 | 7900 | 15000 | 26000 | 44500 | 70000 | – | – |
0,17 | 6300 | 12500 | 22500 | 37000 | 59000 | 100000 | – |
0,18 | 5500 | 11400 | 18300 | 31500 | 50000 | 85000 | – |
0,19 | 4700 | 8900 | 15400 | 26800 | 43000 | 72000 | – |
0,2 | 4000 | 7600 | 13200 | 23000 | 32000 | 62000 | – |
0,22 | 3000 | 5700 | 9900 | 17300 | 28000 | 47000 | – |
0,235 | – | – | – | – | – | – | 100000 |
0,27 | 1630 | 3100 | 5300 | 9500 | 15200 | 25600 | 76000 |
0,3 | 1200 | 2250 | 3950 | 6900 | 11000 | 19000 | 49000 |
0,31 | – | – | – | – | – | – | – |
0,32 | 990 | 1850 | 3250 | 5800 | 9100 | 15700 | 41000 |
0,35 | 750 | 1420 | 2500 | 4400 | 7000 | 12000 | 31500 |
0,37 | 620 | 1200 | 2100 | 3700 | 6000 | 10000 | 26000 |
0,4 | 500 | 960 | 1650 | 2920 | 4800 | 8000 | 21000 |
0,41 | – | – | – | – | – | – | – |
0,42 | 480 | 820 | 1440 | 2500 | 4140 | 7000 | 20400 |
0,45 | 360 | 680 | 1170 | 2040 | 3400 | 5700 | 15000 |
0,47 | 315 | 585 | 1020 | 1770 | 2970 | 5000 | 13300 |
0,5 | 260 | 490 | 860 | 1500 | 2500 | 4200 | 11000 |
0,52 | – | – | – | – | – | – | – |
0,54 | 200 | 390 | 680 | 1180 | 1970 | 3300 | 8800 |
0,6 | 170 | 290 | 500 | 860 | 1450 | 2440 | 6500 |
0,64 | 145 | 250 | 410 | 710 | 1200 | 2000 | 5300 |
0,65 | – | – | – | – | – | – | – |
0,7 | 120 | 200 | 310 | 545 | 930 | 1550 | 4100 |
0,74 | 107 | 175 | 270 | 460 | 790 | 1300 | 3500 |
0,8 | 89 | 146 | 220 | 365 | 620 | 1030 | 2770 |
0,81 | – | – | – | – | – | – | – |
0,84 | 81 | 132 | 197 | 315 | 500 | 890 | 2400 |
0,9 | 70 | 113 | 167 | 260 | 440 | 730 | 1950 |
0,94 | 65 | 103 | 150 | 235 | 387 | 640 | 1730 |
1 | 58 | 91 | 130 | 205 | 328 | 540 | 1450 |
1,1 | 48 | 75 | 106 | 163 | 250 | 400 | 1080 |
1,18 | – | – | – | – | – | – | – |
1,2 | 41 | 64 | 89 | 134 | 200 | 310 | 840 |
1,3 | 36 | 54 | 75 | 111 | 167 | 250 | 660 |
1,4 | 31 | 48 | 65 | 95 | 142 | 210 | 540 |
1,5 | 28 | 43 | 57 | 82 | 120 | 176 | 430 |
1,6 | 25 | 38 | 50 | 73 | 107 | 154 | 360 |
1,65 | – | – | – | – | – | – | – |
1,7 | 23 | 34 | 45 | 64 | 93 | 133 | 300 |
1,8 | 21 | 31 | 41 | 58 | 83 | 117 | 255 |
1,9 | 19,3 | 28 | 37 | 52 | 74 | 104 | 220 |
2 | 18 | 26 | 34 | 47 | 67 | 94 | 195 |
2,2 | 15,5 | 22 | 27,5 | 39 | 53 | 76 | 155 |
2,5 | 13,1 | 18,3 | 23,4 | 31,5 | 44 | 60 | 115 |
2,7 | 12 | 16,4 | 20,8 | 27,7 | 38,5 | 52 | 98 |
3 | 10,5 | 14,3 | 18 | 23,7 | 33 | 43 | 80 |
3,2 | 9,5 | 13 | 16,3 | 21 | 29 | 38 | 68 |
3,5 | 9 | 11,6 | 14,3 | 18,5 | 25 | 33 | 58 |
3,7 | 8,5 | 10,8 | 13,8 | 17 | 23 | 30 | 51 |
4 | 7,9 | 10 | 12 | 15,3 | 20,4 | 26,5 | 44,5 |
4,2 | 7,6 | 9,6 | 11,3 | 14,3 | 18,8 | 23,5 | 40,5 |
4,5 | 7,15 | 9 | 10,4 | 13 | 17,3 | 22 | 36 |
4,7 | 6,95 | 8,8 | 9,8 | 12,3 | 16,2 | 20,3 | 33 |
5 | 6,6 | 8,1 | 9,4 | 11,3 | 14,8 | 18,7 | 29,8 |
5,4 | 6,3 | 7,6 | 8,7 | 10,3 | 13,3 | 16,7 | 26 |
6 | 5,9 | 7 | 7,9 | 9,4 | 11,7 | 14,3 | 22 |
6,4 | 5,7 | 6,8 | 7,4 | 8,8 | 10,8 | 13,3 | 20 |
7 | 5,5 | 6,25 | 6,95 | 8,05 | 9,9 | 11,8 | 17,5 |
7,4 | 5,4 | 6,05 | 6,65 | 7,65 | 9,3 | 11 | 16 |
8 | 5,2 | 5,8 | 6,3 | 7,2 | 8,6 | 10,1 | 14,3 |
8,4 | 5,15 | 5,7 | 6,1 | 6,9 | 8,1 | 9,7 | 13,5 |
9 | 5,1 | 5,5 | 5,9 | 6,6 | 7,7 | 9 | 12,3 |
9,4 | 5,05 | 5,4 | 5,75 | 6,4 | 7,4 | 8,6 | 11,5 |
10 | 5,01 | 5,3 | 5,6 | 6,2 | 7 | 8,1 | 10,8 |
11 | 5 | 5,2 | 5,4 | 5,8 | 6,6 | 7,5 | 9,7 |
12 | – | 5,1 | 5,2 | 5,6 | 6,2 | 7 | 8,9 |
13 | – | 5 | 5,15 | 5,4 | 5,9 | 6,6 | 8,2 |
14 | – | – | 5,05 | 5,25 | 5,7 | 6,2 | 7,7 |
15 | – | – | 5 | 5,15 | 5,5 | 6 | 7,2 |
16 | – | – | – | 5,1 | 5,35 | 5,8 | 6,9 |
17 | – | – | – | 5,05 | 5,2 | 5,6 | 6,6 |
18 | – | – | 5 | 5,15 | 5,5 | 6,3 | |
19 | – | – | – | – | 5,1 | 5,35 | 6,1 |
20 | – | – | – | – | 5,05 | 5,25 | 5,95 |
22 | – | – | – | – | 5 | 5,1 | 5,65 |
25 | – | – | – | – | – | 5 | 5,35 |
27 | – | – | – | – | – | – | 5,2 |
30 | – | – | – | – | 5,05 | ||
35 | – | – | – | – | – | – | 5 |
Таблица определения величин сопротивления покрытия по величинам
затухания сигнала частотой 1000 Гц для трубопроводов диаметром 620 ¸1420
мм
Затухание, мБ | Сопротивление | ||||||
D =620 мм | D =720 мм | D =820 мм | D =920 мм | D = 1020 мм | D =1220 mm | D =1420 мм | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0,31 | 100000 | – | – | – | – | – | – |
0,32 | 92000 | – | – | – | – | – | – |
0,35 | 70000 | – | – | – | – | – | – |
0,37 | 60000 | – | – | – | – | – | – |
0,4 | 47000 | – | – | – | – | – | – |
0,41 | – | 100000 | – | – | – | – | – |
0,42 | 41000 | 94000 | – | – | – | – | – |
0,45 | 34000 | 78000 | – | – | – | – | – |
0,47 | 29500 | 68000 | – | – | – | – | – |
0,5 | 24500 | 57000 | – | – | – | – | – |
0,52 | – | – | 100000 | – | – | – | – |
0,54 | 19400 | 45000 | 89000 | – | – | – | – |
0,6 | 14300 | 36000 | 65000 | – | – | – | – |
0,64 | 11700 | 27000 | 53500 | – | – | – | – |
0,65 | – | – | 100000 | – | – | – | |
0,7 | 9000 | 21000 | 41500 | 80000 | – | – | – |
0,74 | 7700 | 17500 | 35000 | 68000 | – | – | – |
0,8 | 6050 | 14000 | 27500 | 54000 | – | – | – |
0,81 | – | – | – | – | 100000 | – | – |
0,84 | 5250 | 12200 | 24000 | 47000 | 90000 | – | – |
0,9 | 4600 | 9800 | 19500 | 38000 | 73000 | ||
0,94 | 3750 | 8700 | 17000 | 33500 | 63000 | – | – |
1 | 3140 | 7100 | 14300 | 28000 | 53000 | – | – |
1,1 | 2300 | 5400 | 10700 | 21000 | 39500 | – | – |
1,18 | – | – | – | – | – | 100000 | – |
1,2 | 1800 | 4400 | 8300 | 16500 | 30500 | 97000 | – |
1,3 | 1430 | 3300 | 6500 | 13000 | 24000 | 76000 | – |
1,4 | 1150 | 2650 | 5200 | 10400 | 19500 | 61000 | – |
1,5 | 920 | 2100 | 4200 | 8400 | 15500 | 49000 | – |
1,6 | 780 | 1750 | 3600 | 7000 | 13000 | 41000 | – |
1,65 | – | – | – | – | – | – | 100000 |
1 J | 580 | 1470 | 3000 | 5900 | 10800 | 33500 | 90000 |
1,8 | 540 | 1250 | 2500 | 5000 | 9100 | 28500 | 75000 |
1,9 | 460 | 1050 | 2100 | 4200 | 7800 | 24000 | 64000 |
2 | 390 | 900 | 1800 | 3700 | 6700 | 20800 | 57000 |
2,2 | 295 | 680 | 1350 | 2730 | 5000 | 15700 | 43000 |
2,5 | 212 | 460 | 920 | 1850 | 3450 | 10500 | 28000 |
2,7 | 177 | 370 | 730 | 1480 | 2700 | 8400 | 22300 |
3 | 140 | 275 | 530 | 1100 | 2000 | 6200 | 16500 |
3,2 | 115 | 230 | 440 | 900 | 1450 | 5100 | 13500 |
3,5 | 98 | 190 | 340 | 700 | 1250 | 3900 | 10500 |
3,7 | 87 | 163 | 290 | 590 | 1050 | 3300 | 8800 |
4 | 75 | 137 | 242 | 470 | 840 | 2600 | 7000 |
4,2 | 68 | 123 | 215 | 410 | 730 | 2250 | 6000 |
4,5 | 59 | 105 | 193 | 330 | 590 | 1800 | 4900 |
4,7 | 54 | 95 | 164 | 295 | 520 | 1600 | 4600 |
5 | 48,5 | 84 | 143 | 250 | 430 | 1320 | 3600 |
5,4 | 44 | 71 | 118 | 206 | 340 | 1040 | 2800 |
6 | 35 | 58 | 95 | 162 | 260 | 770 | 2050 |
6,4 | 31,5 | 52 | 84 | 120 | 222 | 630 | 1700 |
7 | 27 | 44 | 70 | 115 | 180 | 480 | 1300 |
7,4 | 24,8 | 39,5 | 62 | 102 | 157 | 410 | 1100 |
8 | 22 | 34,6 | 54 | 86 | 132 | 330 | 860 |
8,4 | 20 | 32 | 49 | 79 | 118 | 290 | 750 |
9 | 18,3 | 28 | 43 | 68 | 102 | 240 | 610 |
9,4 | 17,3 | 26,5 | 40 | 63 | 94 | 220 | 535 |
10 | 15,7 | 24 | 36 | 56 | 82 | 190 | 450 |
11 | 13,8 | 20,5 | 31 | 47 | 68 | 150 | 340 |
12 | 12,3 | 18 | 26,8 | 40 | 58 | 125 | 275 |
13 | 11,2 | 16 | 23,5 | 35 | 49,5 | 103 | 220 |
14 | 10,3 | 14,5 | 21 | 31 | 43 | 89 | 183 |
15 | 9,6 | 13 | 18,8 | 27,5 | 38 | 76 | 158 |
16 | 9 | 12 | 17 | 24,8 | 34,5 | 68 | 137 |
17 | 8,5 | 11,3 | 15,7 | 22,4 | 31 | 60 | 118 |
18 | 8 | 10,5 | 14,5 | 20,5 | 28 | 54 | 105 |
19 | 7,7 | 9,9 | 13,5 | 19 | 26 | 49 | 94 |
20 | 7,3 | 9,5 | 12,6 | 17,5 | 24 | 44 | 84 |
22 | 6,8 | 8,6 | 11,2 | 15,3 | 20,05 | 37,5 | 69 |
25 | 6,2 | 7,6 | 9,8 | 13 | 17 | 30 | 54 |
27 | 5,95 | 7Д | 9 | 11,7 | 1,5,2 | 26,4 | 46,6 |
30 | 5,65 | 6,6 | 8,15 | 10,3 | 13,3 | 22,3 | 38,6 |
35 | 5,3 | 5,95 | 7,15 | 8,85 | 11 | 18,7 | 29,8 |
40 | 5,1 | 5,6 | 6,5 | 7,8 | 9,5 | 14,5 | 24 |
45 | 5,02 | 5,3 | 6,05 | 7,1 | 8,45 | 12,6 | 20 |
50 | 5 | 5,15 | 5,7 | 6,55 | 7,65 | 11 | 17 |
60 | – | 5 | 5,3 | 5,85 | 6,65 | 9,1 | 13,3 |
70 | – | – | 5,1 | 5,5 | 6,05 | 7,9 | 11 |
80 | – | – | 5 | 5,2 | 5,65 | 7,05 | 9,5 |
90 | – | – | – | 5,05 | 5,4 | 6,45 | 8,4 |
100 | – | – | – | 5 | 5,2 | 6,05 | 7,65 |
120 | – | – | – | – | 5,05 | 5,55 | 6,6 |
140 | – | – | – | – | 5 | 5,25 | 6 |
160 | – | – | – | – | – | 5,1 | 5,55 |
180 | – | – | – | – | – | 5 | 5,35 |
200 | – | – | – | – | – | – | 5,15 |
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT = 159
мм и DT =
620 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT = 219
мм и DT =
720 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT = 273
мм и DT = 820
мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT =325
мм и DT =
920 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT =377
мм и DT
=1020 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT = 425
мм и DT =
1220 мм
Номограмма определения сопротивления изоляции по затуханию сигнала
с частотой F = 1000 Гц
для DT = 530
мм и DT =
1420 мм









