Линии напряженности. поток вектора
НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Для того, чтобы описать электрическое поле, нужно задать Е в каждой точке поля . Это можно сделать аналитически, выражая зависимость Е(х,у,z) в виде формул. Однако, это можно сделать и графически с помощью так называемых линий напряженности или силовых линий.
Силовой линией,или линией вектора напряженности поля,называют линию, проведенную в электрическом поле, для которой направление касательной в любой точке совпадает с направлением вектора напряженности поля (рис.2)

 `E
`E
Рис.2 `E
Т.к. касательная определяет два взаимно противоположных направления, то силовой линии приписывают определенное направление, отмечая его на чертеже стрелкой.
Густота силовых линий на чертеже отражает величину напряженности поля, а именно, число силовых линий, проходящих через единицу поверхности, перпендикулярной к силовым линиям, равно ( или пропорционально) величине напряженности поля в данном месте. Вследствие наглядности графический способ представления полей широко применяют в электротехнике.
Из сказанного следует, что силовую линию можно провести через всякую точку поля. Далее, т.к. в каждой точке поля вектор напряженности имеет вполне определенное (одно!) положение, то силовые линии нигде не пересекаются.
В качестве примера рассмотрим картину силовых линий точечного заряда. Для точечного заряда `E||`r и линии напряженности направлены по радиусам, проведённым из заряда. Для положительного заряда (q>0) эти линии исходят из заряда и уходят в ¥ (рис.3 а). Для отрицательного заряда (q<0) `E направлен против радиус-вектора `r, а линии напряженности идут из ¥ и сходятся в точке нахождения заряда (рис.3 б). Как видно из рисунка, густота линий убывает обратно пропорционально квадрату расстояния от заряда, т.е. так же, как и
Рис.3.
напряженность поля.
Т.е. густота линий равна отношению полного числа линий N к величине поверхности сферы радиуса r, т.е. N/4pr2~1/r2.
На рис.4 показано электрическое поле между двумя равными по величине точечными зарядами одинаковых и противоположных (рис.5) знаков, расположенными на расстоянии l друг от друга (диполь).
Рис.4. Рис.5. (Дипольный момент Р = q l ).
Связь между электрическим полем и его источником может быть выражена достаточно просто. Для этого введём понятие потока вектора напряженности,которое используется при формулировке важнейших свойств электрического, магнитного и других векторных полей.
Рассмотрим в пространстве некоторое электрическое поле и замкнутую поверхность произвольной формы.
Разделим всю поверхность на столь малые части, что поверхность каждой части (элемента поверхности) можно считать практически плоской; на такой поверхности вектор напряженности электрического поля не будет заметно меняться. Направление элемента поверхности представим вектором нормали. За положительную нормаль к поверхности примем внешнюю нормаль, т.е. нормаль, направленную наружу. Способ разделения поверхности на элементы не имеет значения, пока элементы достаточно малы. Число силовых линий, равных скалярному произведению
N = (`E×`n)dSi = Фi – называется потоком вектора напряженности через элемент поверхности dSi.
Величина Ф может быть >0 и<0, т.к. нормаль может быть как положительной, так и отрицательной.
Теперь сложим потоки через все элементы поверхности и получим поток через всю поверхность
Ф = ò (`E×`n)dS =ò (En ×dS,
где Еn – проекция `Е на направление нормали к площадке dS, где интеграл берется по поверхности S.
Пусть Вас не пугает сложность вычисления таких интегралов для поверхностей сложной формы. Удивительное свойство, которое мы с вами сейчас рассмотрим, делает такие вычисления ненужными!
Теорема Остроградского-Гаусса.
1). Возьмём наиболее простой случай: предположим, что поле создано изолированным положительным точечным зарядом q и что поверхностью является сфера радиуса r, в центре которой расположен точечный заряд (Риc. 6). Чему равен поток Ф через такую поверхность?
Рис.6.
Ответить на этот вопрос легко, т.к. в каждой точке поверхности
`E = (1/4pe0)(q/r3)`r,
а поверхность сферы S=4pr2, тогда
Ф = E×4pr2= (q/4pe0 r2) 4pr2=q/e0.
Как мы видим из этой формулы, поток не зависит от размеров сферы.
2). Покажем теперь, что поток не зависит и от формы поверхности,
окружающей заряд q. Проведем две концентрические сферы разных радиусов. Мы увидим, что число линий напряженности электрического поля, пронизывающих сферы, одинаково. Между этими сферами линии вектора напряженности `Е идут непрерывно, нигде не заканчиваясь и не начинаясь вновь. Поэтому, если мы проведем между этими сферами замкнутую поверхность S1произвольной формы, тоже охватывающую заряд q, то поток вектора напряженности через эту поверхность также будет равен q/e0.
Напомню, что линии напряженности электрического поля начинаются и заканчиваются только на электрических зарядах. Если замкнутая поверхность не охватывает заряда, то поток вектора электрического поля через эту поверхность равен нулю, т.к. число силовых линий, входящих в поверхность, равно числу выходящих из неё.
3). Пусть поле создается не одним точечным зарядом, а произвольной системой точечных зарядов q1, q2, q3…qn. По принципу суперпозиции напряжённость результирующего электростатического поля равна векторной сумме напряжённостей электростатических полей, создаваемых каждым из зарядов в отдельности :
`E = `E1 `E2 `E3 … `En = S`Ei.
поэтому проекция вектора `Е на направление нормали к площади dS равна алгебраической сумме проекций всех векторов `Еi на это направление

Поток напряженности результирующего поля сквозь произвольную замкнутую поверхность S, охватывающую заряды q1, q2, …qk , и не охватывающую заряды qk 1…qm, равен 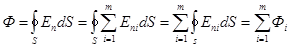 , но Фi=0, если i>k
, но Фi=0, если i>k
поэтому
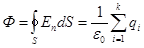 ,т.е.
,т.е.
поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов, охватываемых этой поверхностью, к электрической постоянной.Это и есть теорема Оетроградского -Гаусса применительно к электростатическому полю в вакууме.
Теорема Остроградского-Гаусса выведена нами как прямое следствие из закона Кулона. Она позволяет сравнительно просто рассчитывать электрические поля при симметричных распределениях зарядов и окружающих их диэлектриков.
Для характеристики электрического поля наряду с `Е удобно ввести ещё одну векторную величину `D ,называемую электрическим смещениемили электрической индукцией.Для поля в электрически изотропной среде связь `D и `E в СИ имеет вид
`D = ee0 `E
Тогда к
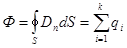 -теорема Остроградского-Гаусса.
-теорема Остроградского-Гаусса.
§
Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Остроградского-Гаусса.
Пример 1. Равномерно-заряженная плоскость.
Имеется безграничная плоскость, заряженная равномерно с поверхностной плотностью заряда s. Найти напряженность Е(х), где х – расстояние до плоскости.
Из симметрии задачи очевидно, что линии напряженности должны быть направлены симметрично в обе стороны от плоскости ^ ей. В этом случае в качестве замкнутой поверхности в теореме Остроградского-Гаусса удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограниченный двумя плоскими основаниями, перпендикулярными к силовым линиям и расположенными по обе стороны заряженной плоскости (рис.7).
Рис. 7. Рис.8.
Т.к. образующие цилиндра параллельны вектору напряженности электрического поля `Е, то поток через боковую поверхность цилиндра равен нулю и поэтому полный поток сквозь цилиндр равен сумме потоков через его основания
Ф =:2ЕS.
Полный заряд, заключенный внутри цилиндра равен Ss. Поэтому применяя теорему О-Г, имеем:
2ЕS =sS/e0, откуда
Е = s/2e0,
т.е. `Е не есть функция расстояния. Следовательно `Е = соnst по величине и по направлению.
Если плотность заряда отрицательная, т.е. (-s), то линии напряжённости имеют противоположное направление.
Пример2.Определим поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноимёнными зарядами (плоский конденсатор, рис.8). Считаем плоскости бесконечными.
Заряженная плоскость каждой пластины создаст по обе стороны от себя напряженность поля, выражаемую формулой ±s/2e0. Внутри металлических пластин и вне конденсатора эти поля направлены противоположно и поэтому в сумме дают нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и, складываясь, дают у поверхности пластин напряженность Е = s/e0. В данном частном случае электрическое поле однородно и поэтому его напряженность у поверхности пластин такая же, как и в других точках поля.
Пример 3. Равномерно заряженный шар.
Рассмотрим электрическое поле между двумя шаровыми концентрическими электродами (рис.9) – шаровой конденсатор. Под действием взаимного притяжения (-) и ( ) заряды расположатся только на поверхности внутреннего шара и на внутренней поверхности внешнего
Рис.9. Рис.10.
электрода. Из условий симметрии очевидно, что заряды на обоих шаровых электродах будут распределены равномерно, и что линии напряженности электрического поля могут быть только радиальными прямыми. Выберем в качестве замкнутой поверхности сферу с радиусом r, расположенную между электродами и имеющую общий центр с обоими электродами.
По теореме Остроградского-Гаусса
Ф = Е(r)4pr2 = q/e0,
откуда
Е(r)=q/4pe0r2. (*)
Эта формула показывает, что напряжённость поля между электродами зависит от расстояния r рассматриваемой точки поля от центра внутреннего шара, но не зависит вовсе от размеров внешнего электрода. Ту же напряженность поля получим, если радиус внешнего электрода будет как угодно велик. Роль внешнего электрода могут играть различные удалённые заземлённые предметы, например стены, пол и потолок комнаты. Поэтому часто говорят просто о поле заряженного шара(рис.10),не указывая, что именно является вторым электродом. Из формулы (*) следует, что электрическое поле шара, равномерно заряженного по поверхности, во внешнем пространстве совпадает с полем точечного заряда, равного полному заряду шара и помещённого в центре шара. Если бы мы рассмотрели шар, заряженный равномерно по объёму, то напряженность поля тоже выражалась бы формулой (*). Напряженность же поля внутри шара в обоих случаях различна. В случае шара, равномерно заряженного по поверхности Е = О в любой внутренней точке. Если же шар заряжен равномерно по объёму, то Е= 0 только в центре шара и с увеличением расстояния r от центра возрастает пропорционально r. В справедливости этого можно убедиться также при помощи теоремы Остроградского-Гаусса.
Пример: «клетка Фарадея».
металл

Рис.11.
§
ПОЛЯ. ГРАДИЕНТ ПОТЕНЦИАЛА.
Для понимания свойств электрического поля большое значение имеет понятие разности потенциалов или электрического напряжения.К этому понятию мы придем, рассматривая работу сил электрического поля.
Предположим, что электрический заряд qперемещается в каком -либо электрическом поле (например, в электрическом поле плоского конденсатора, рис. 12), из некоторой точки 1 в другую точку 2. Так как на заряд в электрическом поле действует сила, то при таком перемещении будет произведена определённая работа А12. Ясно, что если тот же заряд перемещается по прежнему пути в обратном направлении (от точки 2 к точке 1), то величина работы будет та же самая, но изменится её знак, т.е. А12 = -А21.
Покажем, что работа по перемещению заряда в электрическом поле не зависит от формы пути, по которому движется заряд, и определяется только положением точек 1 и 2 – начала и конца пути заряда.
Допустим, что это не так, и что работа А(L)12 при перемещении заряда вдоль контура L (рис.12) не равна работе А (L’) 12 для контура L’, причём оба контура соединяют одни и те же точки 1 и 2.
 –
–

 2 –
2 –

 1
1
 –
–
L L¢
 –
–
 –
–
Рис. 12.
Тогда перемещая заряд по замкнутому контуру, составленному из контуров L и L’, мы найдём, что электрические силы совершают работу
А(L)12 А(L’)21= А(L)12– А(L’)12,
которая не равна нулю. Но это противоречит общему закону сохранения энергии. Если заряды, создающие электрическое поле, неподвижны, то при перемещении подвижного заряда в окружающих телах не происходит никаких процессов. После возвращения заряда в исходную точку 1 мы не имеем никаких изменений в рассматриваемой системе тел и поэтому не можем получить ни выигрыша работы, ни её потери. Это значит, что наше предположение неверно, и что в действительности
А(L)12 =А(L’)12
Т.о., в электростатическом поле работа перемещении заряда между двумя точками не зависит от формы пути, соединяющего эти точки.Иными словами: при перемещении заряда в электростатическом поле по замкнутому контуру работа равна нулю.

Если заряд q0перемещается в поле,создаваемом_системой точечных зарядов q1,q2,…qn , то на него действует сила
 “
“ 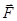 =
= 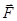 1
1 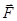 2 ….
2 …. 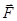 n,
n, 
а работа А равнодействующей силы равна алгебраической сумме работ составляющих сил
А=А1 А2 Аз … Аn.
Полная работа А, как и каждая из работ А1 , А2,.. Аn зависит от начального и конечного положений заряда q, но не зависит от формы его пути. _
Работа, совершаемая силой `F при перемещении заряда q0 на отрезке d,
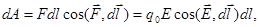
где 
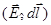
-угол между направлениями векторов `Е и dl.
В случае конечного перемещения заряда q0 източки а в точкув работа сил поля
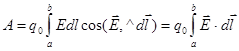
Работа, которую совершают силы электрического поля, перемещая единичный положительный заряд по замкнутому пути L , численно равна
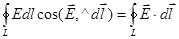
Этот интеграл называется циркуляцией напряженностивдоль замкнутого контура L.
Поскольку работа при перемещении заряда по любому замкнутому контуру равна нулю, то
т.е. циркуляция напряженности электростатического поля вдоль замкнутого контура равна нулю.Силовое поле, напряжённость Е которого удовлетворяет такому условию, называется потенциальным полем.Т.о. электростатическое поле является потенциальным.
РАЗНОСТЬ ПОТЕНЦИАЛОВ.Если в электрическом поле перемещается заряд ( 1), то работа зависит только от существующего электрического поля и поэтому может служить его характеристикой. Она называется разностью потенциаловточек 1 и 2 в данном электрическом поле или электрическим напряжениеммежду точками 1 и 2.
Разность потенциалов двух точек 1 и 2 в электростатическом поле измеряется работой, совершаемой силами поля при перемещении заряда (
1
)
из
точки
1
в 2,
т.е.
(1)
Еl – проекция вектора Е на направление dl. Интегрирование производится вдоль любого контура L, соединяющего рассматриваемые точки, в направлении от точки 1 к точке 2.
Если в электрическом поле перемещается не единичный заряд, а заряд произвольной величины q, то в каждой точке сила, действующая на заряд, увеличится в q раз. Поэтому работа А12, совершаемая силами поля при перемещении q из 1 в 2,равна
А12 =qU12. (2)
Из сказанного следует, что физический смысл имеет только разность потенциаловили напряжение между двумя точками поля, т.к. работа определена только тогда, когда заданы две точки – начало и конец пути. Несмотря на это, часто говорят просто о потенциале или напряжении в данной точке. Однако при этом всегда имеют в виду разность потенциалов, но подразумевают, что одна из точек выбрана заранее. Такую постоянную точку часто выбирают “в бесконечности”, т.е. на достаточном удалении от всех заряженных тел.
Если заряд ( 1) перемещается по замкнутому контуру, например, сначала из 1 в 2 по контуру L (рис.12), а затем от 2 к 1 вдоль L’, то
U12 U21 =U12 -U12 =0 (3)
§
Рассмотрим заряженный уединенный проводник, находящийся в неподвижном диэлектрике (вдали от заряженных тел и других проводников). При сообщении ему некоторого заряда последний распределяется по его поверхности с различной плотностью s. Однако характер этого распределения зависит не от общего заряда q, а только от формы проводника. Каждая новая порция зарядов распределяется по поверхности проводника подобно предыдущей. Т.о., s изменяется пропорционально q. Между зарядом проводника q и его потенциалом U существует прямая пропорциональность:
q = CU (1)
Коэффициент С зависит только от размеров и формы проводника, а также от диэлектрической проницаемости окружающего диэлектрика и ее распределения в пространстве.
Он называется емкостью уединённого проводника.
Пример:Для уединенного проводящего шара радиуса R, несущего заряд q и находящегося в однородной среде с относительной диэлектрической проницаемостью e потенциал
U = q/4pe0eR,
oткуда С = 4pe0eR. (2)
Из последней формулы видно, что ни от материала проводника, ни от формы и размеров возможных полостей внутри проводника его электроёмкость не зависит.
За единицу электроёмкости в СИ,называемой фарадой(Ф), принимается электроёмкость такого уединённого проводника, потенциал которого изменяется на один вольт при сообщении ему заряда в один кулон: 1Ф=1К/В.
Если проводник А не уединённый, т.е. вблизи него имеются другие проводники, то его электроемкость больше, чем у такого же, но уединённого проводника, потому что при сообщении проводнику А заряда q окружающие его проводники заряжаются через влияние. Причём ближайшие к наводящему заряду q оказываются заряды противоположного знака. Эти заряды несколько ослабляют поле, создаваемое зарядом q. Т.о. они понижают потенциал проводника А и повышают его электроёмкость.
Наибольший интерес представляет система, состоящая из двух близко расположенных друг от друга проводников, заряды которых численно равны, но противоположны по знаку. Если проводники находятся вдали от каких бы то ни было заряженных тел и иных проводников, то
U1-U2= U = q /C, или С = q/U, (3)
где С – взаимная электроёмкость двух проводников, зависит от их формы, размеров и взаимного расположения, а также от диэлектрической проницаемости среды.
Важным для практики является случай, когда два разноименно заряженных проводника имеют такую форму и так расположены друг относительно друга, что создаваемое ими электрическое поле полностью или почти полностью сосредоточено в ограниченной части пространства. Такая система проводников называется простым конденсаторомили просто конденсатором, а сами проводники –его обкладками.
Электроёмкость конденсатора представляет собой взаимную ёмкость его обкладок и выражается формулой (3). В зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Вычислим емкость плоского конденсатора.Будем считать, что зазор между пластинами мал по сравнению с их размерами, так что краевыми эффектами можно пренебречь. Если поверхностная плотность заряда s и диэлектриком является вакуум, то
U=sd/e0 ,
где d – расстояние между пластинами.
Но q = sS,
поэтому
С =q/U = e0S /d.
Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостыо e, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то ёмкость будет в e раз больше:
С = ee0S/d.
При уменьшении расстояния d между пластинами ёмкость увеличивается, что можно наблюдать на опыте.
Конденсатор характеризуется не только электроёмкостью, но и так называемым “пробивным напряжением” – разностью потенциалов между его обкладками, при которой может произойти его пробой, т.е. электрический разряд через слой диэлектрика в конденсаторе. Величина пробивного напряжения зависит от свойств диэлектрика, его толщины и формы обкладок.

 Для получения больших электроёмкостей конденсаторы соединяют параллельно, рис.15. C1
Для получения больших электроёмкостей конденсаторы соединяют параллельно, рис.15. C1

 1 C2 2
1 C2 2




C3 Рис. 15.
Пусть электроёмкость конденсаторов С1, С2,…Сn.
В этом случае общим для всех конденсаторов является напряжение U и мы имеем: q1 = С1U, q2= С2 U ,…
Суммарный заряд, находящийся на батарее, равен
q = Sqi = USCi
и поэтому емкость батареи
C = q/U = SCi.
Емкость батареи конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов. Допустимое напряжение на батарее будет равно меньшему допустимому напряжению из всех конденсаторов.
Если к концам батареи последовательно соединенных конденсаторов приложить разность потенциалов U, то крайние пластины зарядятся разноименными зарядами ± q. Вследствие электростатической индукции на всех промежуточных пластинах индуцируются заряды, также численно равные ± q, как это показано на рис.16.
С1 С2 С3



 q -q q -q q -q
q -q q -q q -q
Рис.16.
Т.е. при последовательном соединении одинаковым для всех конденсаторов является заряд q, равный полному заряду батареи, и мы можем записать : U1=q/C1, U2=q/C2 ,…
Напряжение же батареи будет равно сумме напряжений на отдельных конденсаторах:
U = 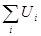 = q
= q 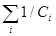 ,
,
Поэтому 1/С = S1/Ci
При последовательном соединении конденсаторов суммируются обратные величины емкостей. В этом случае напряжение на каждом конденсаторе будет меньше напряжения на батарее, и поэтому допустимое рабочее напряжение батареи будет больше, чем у одного конденсатора. В отдельных случаях используют смешанное соединение конденсаторов.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Если обкладки заряженного конденсатора замкнуть металлической проволокой, то в ней возникает электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проволоке определённое количество тепла, а это значит, что заряженный конденсатор обладает энергией.
Вычислим энергию заряженного конденсатора С. Для этого обозначим через U мгновенное значение напряжения на обкладках конденсатора в процессе разряда. Если малое количество заряда dq проходит в процессе разряда с одной обкладки на другую, то работа электрических сил dА будет
dА =U dq.
Выражая в этой формуле заряд обкладок qчерез напряжение
Q = CU, получим
dA = CU dU.
Полную работу, совершаемую электрическими силами за все время разряда, равную энергии конденсатора W, мы получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда). Это дает:
A= – W = C 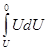 = – CU2/2. (1)
= – CU2/2. (1)
Можно (1) переписать:
W = CU2/2 = q2/2C = qU/2. (2)
А где именно, т.е. в каком месте в конденсаторе локализована эта энергия? – На обкладках конденсатора, т.е. на электрических зарядах, или в его электрическом поле, т.е. в пространстве между обкладками. В дальнейшем мы сможем ответить на этот вопрос, что энергия сосредоточена в электрическом поле.Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию.
Учитывая это, мы можем преобразовать (2) т.о., чтобы в него входила характеристика поля – его напряженность.
Рассмотрим вначале однородное поле и применим формулу (1) к плоскому конденсатору. Мы получим
W = ee0SU2/2d = ee0(U/d)2Sd/2, но
U/d=E, a Sd – объём, занимаемый полем.
Мы видим, что энергия однородного электрического поля пропорциональна объёму, занимаемому полем. Поэтому целесообразно говорить об энергии каждой единицы объёма, или об объёмной плотности энергии электрического поля.Она равна
W1 = ee0E2/2 = ED/2, т.к. V = Sd = 1.
Последнее выражение справедливо только для изотропного диэлектрика.
Если электрическое поле неоднородно, то его можно разбить на элементарные объемы dV и считать, что в пределах бесконечно малого объема это поле однородно. Поэтому энергия, заключенная в объеме поля dV, будет W1dV, а полная энергия любого электрического поля может быть представлена в виде
W = (e0/2) 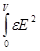 dV,
dV,
Причем интегрирование проводится по всему объему V, где имеется электрическое поле.
§
Электрическим токомназывается направленное движение электрических зарядов. Ток, возникающий в проводнике вследствие того, что в нем создастся электрическое поле, называется током проводимости.При движении зарядов нарушается их равновесное распределение: поверхность проводника уже не является эквипотенциальной и электрические силовые линии не направлены ^ ей, т.к. для движения зарядов необходимо, чтобы на поверхности проводника тангенциальная составляющая напряженности электрического поля не равнялась нулю (Et¹ 0). Но тогда и внутри проводника должно существовать электрическое поле, ибо, как известно из электростатики, внутри проводника нет поля лишь в случае равновесного распределения зарядов по поверхности этого проводника. Перемещение зарядов – электрический ток – продолжается до тех пор, пока все точки проводника не станут эквипотенциальными.
Т.о., для появления и существования электрического тока проводимости необходимы два условия.
Первое- наличие в данной среде носителей заряда,т.е. заряженных частиц, которые могли бы в ней перемещаться.Такими частицами, как мы убедимся далее, в металлах являются электроны проводимости, в жидких проводниках (электролитах) – положительные и отрицательные ионы; в газах – положительные ионы и электроны, а также иногда и отрицательные ионы.
Второе – наличие в данной среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов.Для того чтобы ток был длительным, энергия поля должна все время пополняться, иными словами, нужен источник электрической энергии-устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В зависимости от свойств этих источников в электротехнике различают источники напряжения и источники тока. Поэтому во избежание неточностей мы будем в дальнейшем пользоваться только термином “источник электрической энергии”.
Упорядоченное движение зарядов можно осуществить и другим способом – перемещением в пространстве заряженного тела (проводника или диэлектрика). Такой электрический ток называется конвекционным током.Например, движение по орбите Земли, обладающей избыточным отрицательным зарядом, можно рассматривать как конвекционный ток.
За направление тока условно принимают направление движения положительных зарядов.
Для характеристики электрического тока через какую либо поверхность (например, в случае тока проводимости – через поперечное сечение проводника) вводится понятие силы тока.
Силой токаназывается физическая величина I, равная отношению заряда dq, переносимого через рассматриваемую поверхность S за малый промежуток времени dt, к величине этого промежутка:
I=dq/dt (1)
Если сила тока и его направление не изменяются с течением времени, то ток называется постоянным.Сила постоянного тока
I=q/t, (2)
где q – заряд, переносимый через поверхность S за конечный промежуток t.
Для того чтобы ток проводимости был постоянным, заряды не должны накапливаться или убывать ни в одной части проводника. Поэтому цепь постоянного тока должна быть замкнутой,а суммарный электрический заряд, который поступает за 1 секунду. сквозь поверхность S1 в объем проводника, заключенный между двумя произвольно выбранными поперечными сечениями S1 и S2 (рис.1), должен быть равным суммарному заряду, выходящему из этого объема за то же время сквозь поверхность S2 Т.о., сила постоянного тока I во всех сечениях проводника одинакова.


 I I
I I
Рис.1 S2
S1
Единица силы тока в СИ– ампер(А) – определяется на основании электромагнитного взаимодействия двух параллельных прямолинейных проводников, по которым протекает постоянный ток. Из (2) следует, что 1А – равен силе постоянного электрического тока, при котором через поперечное сечение проводника в 1секунду переносится заряд, равный 1К:
1А=1К/с.
Для характеристики направления электрического тока в различных точках рассматриваемой поверхности вводится вектор плотности электрического тока,который совпадает по направлению с движением положительно заряженных частиц – носителей заряда и численно равен отношению силы тока dI сквозь малый элемент поверхности, нормальный к направлению движения заряженных частиц, к площади dS^ этого элемента:
`J = dI/ dS^, (3)
В СИ плотность тока измеряется в (А/м2).
Очевидно, что dI = Jсоsa dS = Jn dS , или dI = `J 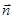 dS,
dS,
где `n – единичный вектор, перпендикулярный площадке dS, Jn – проекции `J на направление нормали `n.
Сила тока через произвольную поверхность S равна
I = òJn dS = ò J dS,
где интегрирование проводится по всей площади этой поверхности. В дальнейшем S- это поперечное сечение проводника. Для постоянного тока I = JS (4)
В цепи постоянного тока, состоящей из проводников с переменной площадью поперечного сечения, рис. 1, плотности тока в различных сечениях S1 и S2 обратно пропорциональны площадям этих сечений:
J1: J2 = S2 : S1.
§
Е12 = 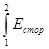 dl.
dl.
Электродвижущая сила численно равна работе, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2.
Эта работа проводится за счет источника электрической энергии. Поэтому величину Е12 можно также называть э.д.с, источника электрической энергии, включенного на участке цепи 1-2. В СИ э.д.с. выражается в вольтах.
Ранее в электростатике мы определили U12 = U1 – U2 как напряжение, приложенное к проводнику. А напряжением на участке цепи 1-2 называется физическая величина U12 численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2 :
U12 = 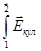
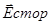 )d
)d 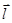 =
= 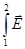
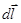 , или
, или
U12 = (U1 – U2) E12. (10)
Это выражение (10) является обобщением понятия напряжения, введенного в электростатике.
Выражение (9) можно переписать
IR12 = (U1 – U2) E12. – обобщенный закон Ома для участка цепи: (11)
или IR12 = U12
произведение сопротивления участка цепи на силу тока в нем равно сумме падения электрического потенциала на этом участке и э д.с. всех источников электрической энергии, включенных на участке.
Обобщенный закон Ома выражает закон сохранения и превращения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для участков электрической цепи, не содержащих источников электрической энергии и называемых, пассивными участками, так и для активных участков, содержащих указанные источники.
При определении E12 в (11) нужно пользоваться следующим правилом знаков для э.д.с. источников, включенных на участке 1-2: если напряженность поля сторонних сил в источнике совпадает по направлению с током в участке цепи, т.е. если внутри источника ток идет от катода к аноду , то при подсчете э.д.с. этого источника нужно считать положительной (рис.За). Если же ток внутри источника идет от анода к катоду, то э.д.с. этого источника следует считать отрицательной (рис.Зб).


 Е, r E,r
Е, r E,r







 1 2 1 2
1 2 1 2
I – I –
Ir = (U1 – U2) E Ir = (U1 – U2) – E
Рис.3а Рис.3б
Для неразветвленной замкнутой цепи сила тока одинакова, и такую цепь можно рассматривать как участок, концы которого совпадают, так что U1 – U2 и R12 = R – общее сопротивление цепи, тогда
RI = Е,
где Е – алгебраическая сумма э.д.с., приложенных к этой цепи.
Если замкнутая цепь состоит из источника электрической энергии с э.д.с. Е и внутренним сопротивлением r, а также внешней части цепи, имеющей сопротивление R, то
E, r



 1 – 2
1 – 2
K I
 R
R
Рис.4.
Разность потенциалов на электродах источника равна напряжению на внешней части цепи
U1 – U2 = RI = E – Ir.
Если с помощью ключа К цепь разомкнуть, то ток в ней прекратится и разность потенциалов на клемах источника будет равна его э.д.с.
На практике часто приходится рассчитывать сложные цепи постоянного тока. Решение этой задачи значительно облегчается, если воспользоваться двумя правилами Кирхгофа.
Назовем узлом любую точку разветвленной цепи в которой сходятся более двух проводников. Тогда первое правило: алгебраическая сумма токов, сходящихся в узле, равна нулю:
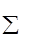 Ik =0, где (12)
Ik =0, где (12)
 n- число проводников, сходящихся в узле, а Ik – токи в них.
n- число проводников, сходящихся в узле, а Ik – токи в них.
I1


 I5 I2
I5 I2
I4 I3
Рис.4.
Токи подходящие к узлу, считают положительными, а токи , отходящие от него – отрицательными.
Второе правило: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I на сопротивления R соответствующих участков этого контура равна алгебраической сумме э.д.с. Е в контуре:
 , (13)
, (13)
где n – число отдельных участков, на которые контур разбивается узлами.
Для составления (13) необходимо условиться о направлении обхода контура (по часовой стрелке или против нее). Выбор этого направления совершенно произволен. Все токи Ik, совпадающие по направлению с направлением обхода контура, считаются положительными. Э.д.с. источников тока, включенных на различных участках контура, считают положительными, если они создают ток, направленный в сторону обхода контура.
Дня поддержания в цепи постоянного тока необходимо совершать работу по перемещению зарядов. Если сила тока в участке цепи равна I, то за время t пройдет заряд It, и поэтому работа электрического тока в этом участке будет:
A = UIt,
т.к. U = IR,
то A = RI2t.
Мощность постоянного электрического тока Р равна:
P = dA/dt = UI = I2R.
Энергия электрического тока в проводнике непрерывно расходуется и переходит в другие формы энергии. Действительно, проводник, по которому течет электрического ток, нагревается и в нем выделяется некоторое количество тепла Q. Если при этом не происходит переход электрической энергии в др. виды энергии (например, в химические превращения, совершаемые током), то по закону сохранения энергии
А = Q = I2Rt = Iut = U2t/R [Дж] – интегральный закон Джоуля-Ленца.
МАГНИТНОЕ ПОЛЕ ТОКОВ. МАГНИТНАЯ ИНДУКЦИЯ. ЗАКОН БИО – САВАРА – ЛАПЛАСА.
Из школьного курса физики Вы знаете, что в пространстве, окружающем намагниченные тела и вокруг проводников с электрическим током существует магнитное поле, которое легко обнаружить по силовому действию, оказываемому им на проводники с током или постоянные магниты. Магнитное поле обладает энергией, свойством инерции и оно столь же материально, как и электрическое поле. Вы уже знаете, что постоянные магниты двумя разноименными полюсами – северным, или положительным, и южным, или отрицательным. Одноименные полюса взаимно отталкиваются, а разноименные -взаимно притягиваются.
Многочисленные опыты показывают, что магнитное (М) поле тесно связано с электрическим током. Электрический ток порождает в пространстве вокруг себя М поле, а проходя в М поле другого тока испытывает со стороны последнего механические воздействия. Поскольку электрический ток представляет собой поток движущихся заряженных частиц, то это означает, что магнитное поле порождается движущимися зарядами, и что другие движущиеся заряды испытывают в этом поле действия механических сил.
Покоящиеся заряды взаимодействуют по закону Кулона. Это взаимодействие сохраняется и при любом движении зарядов. Но в случае движения зарядов возникает дополнительное М поле, обуславливающее появление добавочного магнитного взаимодействия.
Повторяю, важнейшая особенность М поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды.
Основной характеристикой магнитного поля служит вектор магнитной индукции `В. Вектор магнитной индукции `В в произвольной точке поля совпадает по направлению с силой, которая действует на северный полюс бесконечно малой магнитной стрелки, помещенной в эту точку поля. Такая магнитная стрелка не может своим присутствием исказить то поле, в которое она вносится. Сила, действующая со стороны М поля на южный полюс стрелки, направлена в сторону, противоположную вектору `В. Следовательно в магнитном поле на магнитную стрелку действует пара сил, поворачивающая ее т.о., чтобы ось стрелки, соединяющая южный полюс с северным, совпала с направлением поля, т.е. вектора `В. В дальнейшем мы дадим более точное определение `В.
Для графического изображения магнитных полей пользуются линиями магнитной индукции.
Линиями магнитной индукции называются линии, проведенные в магнитном поле так, что вектор `В в каждой точке этой линии направлен по касательной к ней. Картины плоских сечений простейших магнитных полей известны из курса физики средней школы.
Направление линий индукции магнитного поля тока определяется по известному правилу буравчика: если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции.
Линии индукции магнитного поля ни в каких точках поля не могут обрываться, т.е. не начинаться не оканчиваться. Эти линии либо замкнуты, либо идут из бесконечности в бесконечность. Поля, обладающие замкнутыми силовыми линиями, называются вихревыми полями. Магнитное поле есть вихревое поле.
Сколь угодно малая часть постоянного магнита всегда имеет оба полюса. Следовательно, в отличие от электрических зарядов свободных магнитных “зарядов” в природе не существует.
Движение электрических зарядов есть электрический ток. Т.к. магнитных зарядов нет, то магнитного тока не существует. Монополей нет. Полосовой магнитик – магнитный диполь.
Французские ученые Ж.Био и Ф. Савар, исследуя магнитные поля, создаваемые в воздухе прямолинейным током, катушкой с током и т.д. пришли к следующим выводам:
– во всех случаях В~ I;
– В зависит от формы и размеров проводника с током;
-`В в произвольной точке поля зависит от расположения этой точки по отношению к проводнику с током.
Однако получить общий закон, который позволял бы вычислить `В в каждой точке поля создаваемого током, текущим по проводнику любой формы им не удалось. По их просьбе Лаплас обобщил результаты их экспериментов в виде дифференциального закона
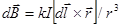 , –закон Био-Савара-Лапласа
, –закон Био-Савара-Лапласа
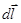 – вектор, численно_равный dl элемента проводника и совпадающий по направлению с током, `г – радиус вектор, проведенный из элемента проводника dl в рассматриваемую точку поля, r =|`r ê, k – коэффициент пропорциональности, определяемый опытным путем.
– вектор, численно_равный dl элемента проводника и совпадающий по направлению с током, `г – радиус вектор, проведенный из элемента проводника dl в рассматриваемую точку поля, r =|`r ê, k – коэффициент пропорциональности, определяемый опытным путем.
Направление `В определяют по правилу векторного произведения или по правилу буравчика. k – зависит от среды. m– относительная магнитная проницаемость среды.
d`B= k2I[ 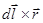 ]/г3.
]/г3.
Для вакуума m =1. В численном виде:
dB = kI dl sina/r2,
где a – угол между векторами 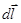 и `r.
и `r.
Закон Б-С-Л позволяет найти`В магнитного поля электрического тока, текущего по проводнику конечных размеров и произвольной формы. В соответствии с принципом суперпозиции `В в любой точке магнитного поля проводника с током I равна векторной сумме D`Вi элементарных магнитных полей, создаваемых всеми отдельными участками Dl этого проводника:
`В = 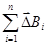 ,
,
где n- общее число участков, на которые разбит проводник.
При n®µ `B =  .
.
Пример 1. Магнитное поле в центре кругового проводника с током.
 R
R



 I `B
I `B
Рис.5.
В этом случае все элементы проводника перпендикулярны к радиус-вектору и sina = 1. Расстояние всех элементов провода от центра круга одинаково и равно радиусу этого круга R. Поэтому
dВ = (mm0/4p)(I/R2)dl. (1 /4p – в системе СИ )
Все элементы тока создают магнитное поле одинакового направления, перпендикулярного к плоскости витка, и поэтому
B = (mm0/4p)(I/R2) 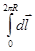 = Imm02pR/4pR2 = mm0I/2R.
= Imm02pR/4pR2 = mm0I/2R.
Направление вектора магнитной индукции `В находим по правилу буравчика (правого).
Вывести самостоятельно формулу для расчета вектора магнитной индукции прямолинейного проводника с током и для соленоида с током I и числом витков N.
§
Ранее мы получили, что
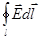 = 0.
= 0.
Это соотношение свидетельствует о том, что электростатическое поле является потенциальным.
Магнитное_поле в отличие от электростатического – непотенциальное поле: циркуляция вектора `В магнитной индукции поля вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле в векторном анализе называется вихревым полем.
Рассмотрим МП бесконечного прямолинейного проводника с током I, находящемся в вакууме. Линии магнитной индукции этого поля представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора `В вдоль произвольной линии магнитной индукции – окружности радиуса r.
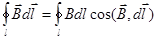 . (1)
. (1)
Вектор `В во всех точках линии численно равен
В = (m0/4p)2I/r – по закону Б.-С.-Л. (2)
и направлен по касательной к этой линии, так что соs(`В,d`l) = 1. Следовательно,
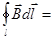 (m0/2p)(I/r)
(m0/2p)(I/r) 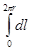 = m0I (3)
= m0I (3)
Из (3) можно сделать два вывода: а)МП прямолинейного тока – вихревое поле, т.е. в нем циркуляция вектора `В вдоль линии магнитной индукции не равна нулю;
б) циркуляция вектора `В магнитной индукции поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на силу тока.
Мы видим, что в (3) не входит зависимость от размеров или формы контура, а можно и доказать, что (3) справедлива для любого замкнутого контура, охватывающего проводник, независимо от формы этого контура.
При выводе (3) считалось, что обход контура происходит по часовой стрелке, При противоположном направлении обхода контура вместо (3) получается
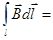 – m0I. (3′)
– m0I. (3′)
Если в этом случае ток I считать отрицательным, то (3′) эквивалентна (3). Поэтому в дальнейшем мы будем пользоваться (3), полагая в ней I>0, если направление тока в проводнике соответствует (по правилу буравчика) направлению обхода контура, и считая I<0 в противном случае.
Если замкнутый контур не охватывает проводника с током, тогда
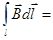 0, (4).
0, (4).
т.е. циркуляция вектора магнитной индукции поля прямолинейного проводника с током вдоль замкнутого контура, не охватывающего этого проводника, равна нулю.
Можно доказать, что (3) и (4) универсальны, т.е. справедливы для МП проводника с током любой формы и любых размеров, а не только для МП бесконечного прямолинейного проводника с током.
В общем случае, когда МП создается системой из n проводников с током I1,…In ,
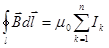 , -закон полного тока для МП в вакууме.
, -закон полного тока для МП в вакууме.
где n- число проводников, охватываемых контуром.
Закон полного тока для МП в вакууме: циркуляция вдоль замкнутого контура вектора индукции МП в вакууме равна произведению магнитной постоянной на алг. сумму токов, охватываемых этим контуром.
ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.
Потоком вектора магнитной индукции или магнитным потоком сквозь малую площадку dS называется физическая величина, равная произведению этой площадки и проекции Вn вектора`В на направление нормали `n к площадке dS:
dФ = ВndS = В dS соs(`В,`n) = `В ×d`S ,
где d`S = `n dS – вектор площадки dS. Интегрируя это выражение по S, получим
Ф= 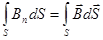 , (1)
, (1)
где Ф – магнитный поток сквозь произвольную поверхность S.
При вычислении этого интеграла векторы `n нормалей к площадкам dS нужно направлять в одну и туже сторону по отношению к поверхности S. Например, если S -замкнутая поверхность, то векторы `n должны быть либо все внешними, либо все внутренними.
Если МП однородное, а S – плоская и S ^`В, то Вn =В = соnst и
Ф = BS. (2)
За единицу магнитного потока принимается магнитный поток сквозь плоскую поверхность единичной площади, расположенную перпендикулярно однородному МП, индукция которого равна единице. Единица магнитного, потока в СИ называется вебером (Вб):
1Вб=1(В×с/м2)×1м2 = 1В×с,
В электродинамике доказывается следующая теорема Остроградского-Гаусса для МП: магнитный поток сквозь произвольную замкнутую поверхность равен нулю:
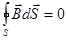 (3)
(3)
Эта теорема является математическим следствием отсутствия в природе магнитных «зарядов” на которых могли бы начинаться и заканчиваться линии магнитной индукции.
СВЕТОВЫЕ ВОЛНЫ
Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других – как поток особых частиц (фотонов). Длительный путь развития учения о свете привел к современным представлениям о двойственной корпускулярно-волновой природе света. Мы с Вами вначале рассмотрим круг явлений, в основе которых лежит волновая природа света.
Теоретические исследования Максвелла о распространении электромагнитных волн, экспериментальные измерения скорости их распространения в пустоте, оказавшейся равной скорости распространения света в пустоте, и другие исследования позволили выдвинуть предположение о чисто электромагнитной природе света.
Электромагнитная теория светаявилась существенным шагом вперед в понимании природы оптических явлений. Свет оказался частным случаем электромагнитных волн с длиной волны от l = 400 нм (фиолетовый) до l=7бО нм (красный). Только этот интервал длин электромагнитных волн оказывает непосредственное воздействие на наш глаз и является собственно светом. Однако и более коротковолновое (l<400 нм –ультрафиолетовое) и более длинноволновое излучение (l>760 нм -инфракрасное) имеют качественно одну и ту же электромагнитную природу и отличаются лишь методами их возбуждения и обнаружения.
В электромагнитной волне колеблются векторы `Е и `Н, причем `Е^`Н (рис.1). Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями вектора напряженности электрического поля `Е, о котором говорят поэтому как о световом векторе.О магнитном векторе `Н световой волны мы упоминать почти не будем.
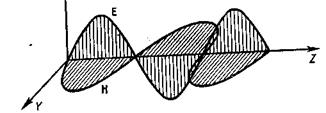
Рис.1. Взаимное расположение векторов `Е и `Н в световой волне.
Модуль амплитуды светового вектора мы будем обозначать А (иногда Ем). Соответственно изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, будет описываться уравнением
Е = Асоs(wt – kr a) – уравнение световой волны (1)
где k – волновое число (k = 2pl), r- расстояние, отсчитываемое вдоль направления распространения световой волны. Для плоской световой волны, распространяющейся в непоглощающей среде, А = const, для сферической волны А убывает как 1/r и т.д.
Отношение скорости распространения световой волны в вакууме (с) к ее скорости в некоторой среде V называется абсолютным показателем преломленияэтой среды и обозначается буквой n. Таким образом,
n = с/ V. (2)
Из электромагнитной теории следует, что n = Öem, где e и m – диэлектрическая и магнитная проницаемости среды. Для подавляющего большинства прозрачных веществ m практически не отличается от единицы. Поэтому можно считать, что n = Öe. Эта формула связывает оптические и электрические свойства вещества. В эту формулу надо подставлять e, полученное для соответствующей частоты, так как n зависит от частоты (длины волны) света.
Значения показателя преломления характеризуют оптическую плотность cреды. Среда с большим n называется оптически более плотной, чем cреда с меньшим n, и наоборот.
Как уже отмечалось, длины волн видимого света l = 400 – 760 нм. Эти значения относятся к световым волнам в вакууме, В веществе длины световых волн будут иными. В случае колебаний частоты n длина волны в вакууме равна l0 = c/n. В среде, в которой фазовая скорость световой волны V = с/n, длина волны имеет значение
l = Vn = c/nn =l0/n.
Т.о. длина световой волны в среде с показателем преломления n связана с длиной волны в вакууме соотношением
l = l0 n.
Частоты видимых световых волн лежат в пределах
n = (3,9-: 7,5) 1014 Гц.
Частота изменений плотности потока энергии, переносимой волной, будет еще больше (она равна 2n). Уследить за столь быстрыми изменениями потока энергии не могут ни глаз, ни приборы, вследствие чего они регистрируют усредненный по времени поток.
Модуль среднего по времени значения плотности потока энергии, переносимой световой волной носит название интенсивности света Iв данной точке пространства. Плотность потока электромагнитной энергии определяется вектором Пойтинга S. Следовательно,
I=|<S>|= |<[ЕН]>|.
Измеряется интенсивность либо в энергетических единицах (Вт/м2), либо в световых единицах, носящих название (лм/м2). Поскольку для электромагнитной волны напряженность Е ~ Н, тогда
I~А2.
Линии, вдоль которых распространяется световая энергия, называются лучами. Усредненный вектор Пойтинга <S> направлен в каждой точке по касательной к лучу. В изотропных средах это направление совпадает с нормалью к волновой поверхности, т.е. с направлением волнового вектора `k. Модуль ê`kê = k – волновое число.
Несмотря на то, что световые волны поперечны, они не обнаруживают асимметрии относительно луча. Это обусловлено тем, что в естественном свете имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу, рис.1а. Излучение светящегося тела слагается из волн, испускаемых его атомами, которые (волны), налагаясь друг на друга, образуют испускаемую телом световую волну. В результирующей волне колебания различных направлений представлены с равной вероятностью.

 Луч света
Луч света
`Е
Рис.1а. Колебания вектора `Е в световой волне естественного света.
В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной проходящей через луч плоскости, свет называется плоско- (или линейно-) поляризованным. Упорядоченность может заключаться в том, что вектор `Е поворачивается вокруг луча, одновременно пульсируя по величине. В результате конец вектора Ё описывает эллипс. Такой свет называется эллиптически – поляризованным. Если конец вектора Ё описывает окружность, свет называется поляризованным по кругу.
§
Пусть в данную точку пространства приходят две световые волны одинаковой частоты, которые возбуждают в этой точке колебания одинакового направления (обе волны поляризованы одинаковым образом):
Когерентностьюназывается согласованное протекание нескольких колебательных или волновых процессов. Степень согласования может быть различной. Соответственно вводится понятие степени когерентностидвух волн.
Пусть в данную точку пространства приходят две световые волны одинаковой частоты, которые возбуждают в этой точке колебания одинакового направления (обе волны поляризованы одинаковым образом):
Е = А1соs(wt a1),
Е = A2cos(wt a2), тогда амплитуда результирующего колебания
А2 = А12 А22 2А1А2соsj, (1)
где j = a1 – a2 = const.
Если частоты колебаний в обеих волнах w одинаковы, а разность фаз j возбуждаемых колебаний остается постоянной во времени, то такие волны называются когерентными.
Приналожении когерентных волн они дают устойчивое колебание с неизменной амплитудойА = соnst, определяемой выражением (1) и в зависимости от разности фаз колебаний лежащей в пределах
|а1 –А2ê £ A £ а1 А2.
Т.о., когерентные волны при интерференции друг с другом дают устойчивое колебание с амплитудой не больше суммы амплитуд интерферирующих волн.
Если j = p, тогда соsj = -1 и а1 = А2, a амплитуда суммарного колебания равна нулю, и интерферирующие волны полностью гасят друг друга.
В случае некогерентных волн j непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение <cоsj>t = 0. Поэтому
А2> = <А12> <А22>,
откуда интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:
I = I1 I2 .
В случае когерентных волн, соsj имеет постоянное во времени значение (но свое для каждой точки пространства), так что
I = I1 I2 2Ö I1 × I2 cosj (2)
В тех точках пространства, для которых соsj >0, I> I1 I2; в точках, для которых соsj<0, I<I1 I2. При наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других -минимумы интенсивности.Это явление называется интерференциейволн. Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: I1=I2. Тогда согласно (2) в максимумах I = 4I1, в минимумах же I = 0. Для некогерентных волн при том же условии получается всюду одинаковая интенсивность I = 2I1.
Все естественные источники света (Солнце, лампочки накаливания и т.д.) не когерентны.
Некогерентность естественных источников света обусловлена тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью порядка 10-8с и протяженностью около 3 м. Фаза нового цуга никак не связана с фазой предыдущего цуга. В испускаемой телом световой волне излучение одной группы атомов через время порядка 10-8с сменяется излучением другой группы, причем фаза результирующей волны претерпевает случайные изменения.
Некогерентными и не могущими интерферировать др. с др. являются волны, испускаемые различными естественными источниками света.А можно ли вообще для света создать условия, при которых наблюдались бы интерференционные явления? Как, пользуясь обычными некогерентными излучателями света, создать взаимно когерентные источники?
Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником света, на две части, Если заставить эти две волны пройти разные оптические пути, а потом наложить их др. на др., наблюдается интерференция. Разность оптических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн. Если эта разность ³1м, наложатся колебания, соответствующие разным цугам, и разность фаз между ними будет непрерывно изменяться хаотическим образом.





 Пусть разделение на две когерентные волны происходит в точке О (рис.2).
Пусть разделение на две когерентные волны происходит в точке О (рис.2).
О n1 S1
n2 S2 P `V
Рис.2.
До точки Р первая волна проходит в среде показателем преломления n1 путь S1, вторая волна проходит в среде с показателем преломления n2 путь S2. Если в точке О фаза колебания равна wt, то первая волна возбудит в точке Р колебание А1соsw(t – S1/V1), а вторая волна -колебание А2соsw(t – S2/V2), где V1 и V2 – фазовые скорости. Следовательно, разность фаз колебаний, возбуждаемых волнами в точке Р, будет равна
j = w(S2/V2 – S1/V1) = (wc)(n2S2 – n1S1).
Заменим w/с через 2pn/с = 2p/lо (lо – длина волны в),тогда
j = (2p/lо)D, где (3)
D= n2S2 – n1S1 = L2 – L1
есть величина, равная разности оптических длин, проходимых волнами путей, и называется оптической разностью хода.
Из (3) видно, что если оптическая разность хода равна целому числу длин волн в вакууме:
D = ±mlо (m = 0,1,2 ), (4)
то разность фаз оказывается кратной 2p и колебания, возбуждаемые в точке Р обеими волнами , будут происходить с одинаковой фазой. Т.о., (4) есть условие интерференционного максимума.
Если оптическая разность хода D равна полуцелому числу длин волн в вакууме:
D = ± (m 1/2)lо (m =0, 1,2, …), (5)
то j = ± (2m 1)p, так что колебания в точке Р находятся в противофазе. Следовательно, (5) есть условие интерференционного минимума.
Принцип получения когерентных световых волн разделением волны на две части, проходящие различные пути, может быть практически осуществлен различными способами – с помощью экранов и щелей, зеркал и преломляющих тел.
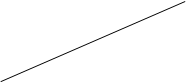
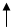 Впервые интерференционную картину от двух источников света наблюдал в 1802 году английский ученый Юнг. В опыте Юнга (рис.3) свет от точечного источника (малое отверстие S) проходит через две равноудаленные щели (отверстия) А1 и А2, являющиеся как бы двумя когерентными источниками (две цилиндрические волны). Интерференционная картина наблюдается на экране Ё, расположенном на некотором расстоянии l параллельно А1А2. Начало отсчета выбрано в точке 0, симметричной относительно щелей.
Впервые интерференционную картину от двух источников света наблюдал в 1802 году английский ученый Юнг. В опыте Юнга (рис.3) свет от точечного источника (малое отверстие S) проходит через две равноудаленные щели (отверстия) А1 и А2, являющиеся как бы двумя когерентными источниками (две цилиндрические волны). Интерференционная картина наблюдается на экране Ё, расположенном на некотором расстоянии l параллельно А1А2. Начало отсчета выбрано в точке 0, симметричной относительно щелей.
x


 P
P
A1 S1

 Плоская св. S O
Плоская св. S O



 волна
волна
 A2 S2l
A2 S2l
 Е
Е
Рис.3
Усиление и ослабление света в произвольной точке Р экрана зависит от оптической разности хода лучей D =L2 – L1. Для получения различимой интерференционной картины расстояние между источниками А1А2=d должно быть значительно меньше расстояния до экрана l. Расстояние х, в пределах которого образуются интерференционные полосы, значительно меньше l. При этих условиях можно положить S2 – S1 » 2l. Тогда S2 – S1 » xd/l. Умножив на n,
подучим
D = nxd/l. (6)
Подставив (6) в (4) получим, что максимумы интенсивности будут наблюдаться при значениях х, равных
хmax = ± mll/d (m = 0, 1,2,.,,.). (7)
Здесь l = l0/n – длина волны в среде, заполняющей пространство между источниками и экраном.
Координаты минимумов интенсивности будут:
хmin = ±(m 1/2)ll/d (m = 0,1,2,…). (8)
Расстояние между двумя соседними максимумами интенсивности называется расстоянием между интерференционными полосами,а расстояние между соседними минимумами – шириной интерференционной полосы.Из (7) и (8) следует, что расстояние между полосами и ширина полосы имеют одинаковое значение, равное
Dх = ll/d. (9)
Измеряя параметры, входящие в (9), можно определить длину волны оптического излучения l. Согласно (9) Dх пропорционально 1/d, поэтому чтобы интерференционная картина была четко различима, необходимо соблюдение упоминавшегося выше условия: d<< l. Главный максимум, соответствующий m = 0, проходит через точку 0. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m =1), второго (m = 2) порядков и т.д.
Такая картина справедлива при освещении экрана монохроматическим светом (l0 = const). При освещении белым светом интерференционные максимумы (и минимумы) для каждой длины волны будут, согласно формуле (9), смещены друг относительно друга и иметь вид радужных полос. Только для m = 0 максимумы для всех длин волн совпадают, и в середине экрана будет наблюдаться светлая полоса, по обе стороны от которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т д. (ближе к центральной светлой полосе будут находиться зоны фиолетового цвета, дальше – зоны красного цвета).
Интенсивность интерференционных полос не остается постоянной, а изменяется вдоль экрана по закону квадрата косинуса.
Наблюдать интерференционную картину можно с помощью зеркала Френеля, зеркала Лойда, бипризмы Френеля и других оптических устройств, а также при отражении света от тонких прозрачных пленок.
§
Большой практический интерес представляет интерференция в тонких пластинках и пленках.
Пусть на тонкую плоскопараллельную пластину толщиной b, изготовленную из прозрачного вещества с показателем преломления n, из воздуха (nвозд » 1) падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей (рис.4), под углом Q1 к перпендикуляру.
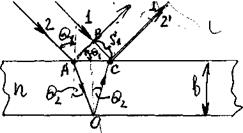
Рис.4.
На поверхности пластины в точке А луч разделится на два параллельных луча света, из которых один образуется за счет отражения от верхней поверхности пластинки, а второй – от нижней поверхности. Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
D = nS2 – S1 ± l0/2
где S1 – длина отрезка АВ, а S2 – суммарная длина отрезков АО и ОС, а член ± l0/2 обусловлен потерей полуволны при отражении света от границы раздела двух сред с различными показателями преломления.
Из геометрического рассмотрения получается формула для оптической разности хода дучей1и2:
D = 2bÖ(n2 – sin2Q1) = 2bn соsQ2,
а с учетом потери полуволны для оптической разности хода получим
D = 2bÖ(n2 – sin2Q1) ± l0/2 = 2bn соsQ2 ± l0/2. (10)
Вследствие ограничений, накладываемых временной и пространственной когерентностью, интерференция при освещении пластинки например солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей
степенью когерентности (например, лазером) интерференция, наблюдается и при отражении от более толстых пластинок или пленок.
Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает лучи в одной из точек экрана, расположенного в фокальной плоскости линзы (рис.5). Освещенность в произвольной точке Р экрана зависит от значения величины D, определенной по формуле (10). При D = mlо получаются максимумы, при D = (m 1/2)lо – минимумы интенсивности (m – целое число).
Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом (рис.5). Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом в), после отражения от обеих поверхностей пластинки соберутся линзой в точке Р и создадут в этой точке освещенность, определяемую значением оптической разности хода.
E
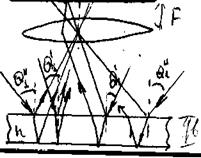 Рис.5.
Рис.5.
Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом Q1¢ соберутся линзой в других точках, отстоящих от центра экрана О на такое же расстояние, как и точка Р. Освещенность во всех этих точках будет одинакова. Т.о. лучи, падающие на пластинку под одинаковым углом Q1¢, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром в точке О. Аналогично, лучи, падающие под другим углом Q”1 создадут на экране совокупность одинаково (но иначе, поскольку А иная) освещенных точек, расположенных по окружности другого радиуса.
В результате на экране возникнет система чередующихся светлых и темных круговых полос с общим центром в точке O). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом Q1. Поэтому получающиеся в описанных условиях интерференционные полосы носят назв. полос равного наклона.При ином расположении линзы относительно пластинки (экран во всех случаях должен совпадать с фокальной плоскостью линзы) форма полос равного наклона будет другой. Роль линзы может играть хрусталик глаза, а экрана – сетчатка глаза.
Согласно (10) положение максимумов зависит от lо. Поэтому в белом свете получается совокупность смещенных др. относительно др. полос, образованных лучами разных цветов, и интерференционная картина приобретает радужную окраску.
Интерференционная картина от тонкого прозрачного клина переменной толщины была изучена еще Ньютоном. Пусть на такой клин (рис.6) падает параллельный пучок лучей.
Рис.6.
Теперь лучи, отразившиеся от разных поверхностей клина, не будут параллельными. Но и в этом случае отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем наблюдаться интерференционная картина в виде полос, параллельных вершине клина 0. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Практически полосы равной толщины наблюдают, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик, а роль экрана – сетчатка глаза. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки представляется имеющей радужную окраску. Такую окраску имеют, например, расплывшиеся по поверхности воды тонкие пленки нефти и масла, а также мыльные пленки. Заметим, что интерференция от тонких пленок может наблюдаться не только в отраженном, но и в проходящем свете.
Классическим примером полос равной толщины являются кольца Ньютона, Они наблюдаются при отражении света от соприкасающихся др. с др. плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис.7).
Рис.7. 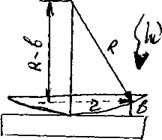
Роль тонкой пленки, от поверхности которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении – эллипсов. Найдем радиусы колец Ньютона, получающиеся при нормальном падении света на пластину. В этом случае sinQ1 = О и D равна удвоенной толщине зазора (предполагается n0 = 1). Из рис. 7 следует, что
R2 = (R – b)2 r2 » R2 – 2Rb r2, (12)
где R – радиус кривизны линзы, r – радиус окружности, всем точкам которой соответствует одинаковый зазор b. Считаем b2 < 2Rb. Из (12) b = г2/2R. Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно к D = 2b = r2/R прибавить lо/2. В результате получится
D = r2/R lо/2. (13)
В точках, для которых
D = m’lо = 2m'(lо/2),
возникают максимумы, в точках, для которых
D = (m’ 1/2)lо =(2m’ 1)(lо/2),
– минимумы интенсивности.
Оба условия можно объединить в одно:
D = mlо/2,
причем четным значениям m будут соответствовать максимумы, а нечетным -минимумы интенсивности. Подставив сюда (13) и разрешив получившееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона:
rm = ÖRlо(m- 1)/2,(m =1,2,3,…). (14)
Четным m соответствуют радиусы светлых колец, нечетным m – радиусы темных колей. Значению m =1 соответствует г = 0, в этой точке наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки.
Измеряя расстояния между полосами интерференционной картины для тонких пластин или радиусы колец Ньютона, можно определить длины волн световых лучей и, наоборот, по известной l найти радиус кривизны линзы.
Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на l0/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.
Другим практическим применением интерференции являются прецизионные измерения линейных размеров. Для этого служат приборы, называемые интерферометрами.
Интерферометры также позволяют определять незначительные изменения показателя преломления прозрачных тел (газов, жидкостей и твердых тел) в зависимости от давления, температуры, примесей и т.п.
ДИФРАКЦИЯ СВЕТА
§
Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает. Для наблюдения дифракции световых волн необходимо создание спец. условий. Это обусловлено малостью длин световых волн. В пределе при l®0 законы волновой оптики переходят законы геометрической оптики. Следовательно, отклонения от законов геометрической оптики при прочих равных условиях оказываются тем меньше, чем меньше длина волны. Между интерференцией и дифракцией нет существ, различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн, а вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути св. волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности св. волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения М расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку М образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера.В противном случае говорят о дифракции Френеля.
Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Однако этот принцип не дает сведений об амплитуде (интенсивности) волн, распространяющихся в различных направлениях. Френель дополнил пр. Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый т.о. принцип Гюйгенса получил название принципа Гюйгенса – Френеля:все источники вторичных волн,расположенные на поверхности фронта волны, когерентны между собой; световая волна в любой точке пространства является результатом интерференции волн, излучаемых вторичными источниками и достигших этой точки. Френель исключил возможность возникновения обратных вторичных волн. Поскольку точек фронта, являющихся когерентными источниками новых волн,бесчисленное множество, то расчет интерференции, в принципе, сводится к довольно громоздкому интегрированию. Для упрощения решения этого вопроса Френелем был предложен метод разделения фронта волны на зоны, так что волны от соседних зон приходят в точку наблюдения в противоположной фазе и ослабляют друг друга. С этим методом зон Френеляознакомимся при анализе важнейшего вопроса: как волновая теория объясняет практическую прямолинейность распространения света и каковы границы применимости законов геометрической оптики, основанных на этой прямолинейности.
Пусть S – точечный источник монохроматического света в однородной среде. По принципу Гюйгенса от него распространяется во все стороны сферическая волна. В некоторый момент времени фронт этой волны занимает положение Ф, рис.1. Рассмотрим произвольную точку М перед фронтом и соединим её прямой линией с источником S .
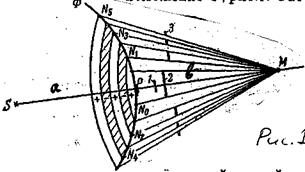
Если бы свет распространялся прямолинейно вдоль луча SРМ, то достаточно было бы поставить на его пути сколь угодно малый экран 1 , чтобы в точке М была полная темнота. Благодаря волновой природе света в точку наблюдения М приходят волны не только от точки Р, но и от всех остальных точек фронта Ф, правда в различных фазах.
Для расчета результатов интерференции Френель предложил провести ряд сфер с центрами в точке М и радиусами, соответственно равными
МN1 = МP l/2,
MN2 = МN1 l/2 = МP 2l/2,
MN3 = МN2 l/2 = МP 3l/2, и т.д. (1)
Тем самым фронт волны Ф разобьется на ряд кольцевых зон, заштрихованных на рис.1 через одну. Волны, приходящие в М от точек каждой последующей зоны, сдвинуты по отношению к волнам, приходящим от соответствующих точек предыдущей зоны, на Я./2, т.е. находятся в противоположных фазах, и их амплитуды при интерференции вычитаются. Из геометрического рассмотрения можно получить выражение для радиуса внешней границы т – ной зоны
Занумеруем величины суммарных амплитуд волн, приходящих в точку М от каждой последующей зоны:
А0, А1, А2, а3, А4, А5, А6, ….
Благодаря различию в расстояниях зон до точки наблюдения и в углах, под которыми видны эти площадки из М, величины этих амплитуд монотонно убывают:
А0 > А1> А2> а3> А4> А5> А6, ….
В качестве допустимого приближения можно принять, что амплитуда колебания от некоторой k – той зоны Френеля Аk равна среднему арифметическому от амплитуд примыкающих к ней зон:
Аk = (Аk 1 Аk-1)/2. (2)
Полная амлитуда волны, приходящей в точку М, равна сумме амплитуд, создаваемых каждой отдельной зоной. При этом амплитуды от всех четных зон надо считать с одинаковым знаком (например, положительными), а амплитуда волн от всех нечетных зон (приходящих в) – с обратным знаком. Т.о.,
А = А0-А1 А2 –А3, А4– А5 …. (3)
Используя (2), можно это выражение представить в виде
А = А0/2 (А0/2 – А1 А2/2) (А2/2 -Аз А4 /2) … » А0/2, (4)
так как оставшаяся часть от амплитуды последней зоны ±Аk/2 практически ничтожно мала.
Т.о., суммарная амплитуда от воздействия всего фронта Ф в точке наблюдения М равна А = А0/2, т.е. эквивалентна половине воздействия нулевойзоны Френеля.
Не следует при этом думать, что в М приходит свет только от всех точек половины нулевой зоны Френеля, остальные же участки фронта Ф, интерферируя, гасят др. др. Если на пути света от точечного источника поставить не слишком большой круглый экран 2 так, чтобы перпендикуляр, опущенный на него из источника света, проходил через его центр, то в М по-прежнему будет свет, хотя и меньшей интенсивности.
Действительно, проведя через край экрана 2 линию МN0, мы можем произвести деление фронта, начиная от точки N0, на такие же зоны Френеля, как и ранее. Повторяя все рассуждения, легко убедиться, что для идеального круглого экрана 2 суммарная амплитуда в М будет А’ = А0¢/2, где а0‘ – амплитуда от нулевой зоны, отсчитываемой от N0. По мере увеличения экрана 2 величина А’ будет убывать, но точка М остается освещенной всегда практически до тех пор, пока экран не закроет достаточно большого числа зон Френеля. Лишь в этом последнем случае станет справедливым положение геометрической оптики, что препятствие, перекрывающее луч SМ, даст в точке наблюдения отсутствие света (геометрическая тень).
Более того, если например, сделать “зонный экран” 3, состоящий из ряда колец, закрывающих все нечетные (или все четные) зоны Френеля, то суммарная амплитуда
А= А0 А2 А4 …. (5)
оказывается даже большей, чем при отсутствии всякого экрана. Т.е такой экран действует подобно собирательной линзе. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, сотв. четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой.По сравнению с перекрывающей зоны амплитудной зонной пластинкойфазовая даст дополнительное увеличение амплитуда в два раза, а интенсивности света – в 4 раза.
Деление фронта волны Ф на зоны Френеля является относительным и зависит от расстояния до точки наблюдения М,
Пренебрегать дифракционными явлениями и рассматривать свет распространяющимся прямолинейно вдоль лучей, исходящих от источника, допустимо лишь, если размеры экрана велики по ср. с размерами зон Френеля. Чем короче l, тем меньше размеры этих зон и тем точнее можно пользоваться приближенными понятиями лучевой (геометрической) оптики. Т.к. для видимого света l = 0,4 – 0,8 мкм, то при наблюдении макроскопических тел этими приближениями можно пользоваться с достаточной точностью. Однако при уменьшении размеров тел начинают проявляться дифракционные явления.
Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса г. Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попадал в центр отверстия. На продолжении этого перпендикуляра возьмем точку Р. Если расстояния а и b удовлетворяют соотношению (*), где m – целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки Р. Из (*) число открытых зон Френеля определяется выражением
m = r02(1/а 1/b)/l. (6)
В соответствии с (3) амплитуда в точке Р будет равна
А = А1 -А2 А3 –А4 ….±Аm (7)
Перед Аm берется знак « », если m нечетное, и минус, если m – четное. Представив (7) в виде, аналогичном (4), и положив выражения в скобках равными нулю, получим
А = А1/2 Аm /2 (m – нечетное),
А=А1/2 Аm-1/2 – Аm (m – четное).
Амплитуды от двух соседних зон практически одинаковы. Поэтому (Аm-1/2) – Аm можно заменить через – Аm/2. В результате получится:
А = А1/2 ± Аm/2,
где знак « » берется для нечетных m и минус – для четных.
Для малых m амплитуда Аm мало отличается от А1. Следовательно, при нечетных m амплитуда в точке Р будет приблизительно равна а1, при четных m – нулю.
А какая будет освещенность в других точках экрана? Вследствие симметричного расположения отверстия относительно прямой SР освещенность в разных точках экрана будет зависеть только от расстояния х от точки Р. Если смещаться по экрану в точку Р¢ и далее, то дифракционная картина будет иметь вид чередующихся светлых и темных концентрических колец. Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает.
Аналогичная картина на экране получается и в рассмотренном выше случае, когда между источником света и экраном помещается непрозрачный круглый диск. Дифракционная картина на экране будет иметь вид чередующихся светлых и темных концентрических колец. В центре картины помещается светлое пятно.
§
Пусть на бесконечно длинную щель падает плоская световая волна, рис.2.
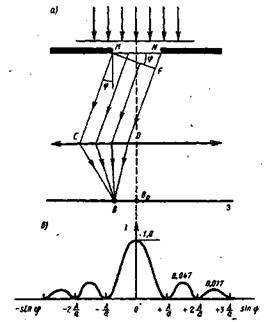
Рис.2.
Поместим за щелью собирательную линзу, а в фокальной плоскости линзы – экран. Волновая поверхность падающей волны, плоскость щели и экран параллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости.
Когда фронт волны дойдет до щели и займет положение MN, то все его точки являются новыми источниками волн, распространяющихся во все стороны вперед от щели. Рассмотрим волны, распространяющиеся от точек плоскости MN в направлении, составляющем некоторый угол j с первоначальным. Эти волны, проходя через линзу, сойдутся в некоторой точке B на экране, расположенном в фокальной плоскости линзы. Лучи, распространяющиеся от щели под различными углами, в результате интерференции дадут дифракционную картину.
Опустим из точки M перпендикуляр MF на направление выделенного пучка лучей. Тогда от плоскости MF и далее до фокальной плоскости Е параллельные лучи не меняют своей разности хода. Разность хода, определяющая условия интерференции, возникает лишь на пути от исходного фронта MN до плоскости MF и различна для разных лучей.
Для расчета интерференции всех этих лучей применим метод зон Френеля. Для этого мысленно разделим линию NF на ряд отрезков длиной l/2. На расстоянии NF = аsinj уложится
Z = (sinj)/(l/2) (1)
таких отрезков. Проводя из концов этих отрезков линии, параллельные MF, до встречи их с MN, мы разобьём фронт волны в щели на ряд полосок одинаковой ширины. Эти полоски и являются в данном случае зонами Френеля. Отсюда следует, что волны, идущие от каждых двух соседних зон Френеля, приходят в точку B в противоположной фазе и гасят др. др. Если число зон четное, z = 2k (где k – целое число, неравное нулю), то каждая пара соседних зон взаимно погасит др.др., так что при данном угле j на экране будет минимум освещенности. Углы j, соответствующие этим минимумам освещенности, находятся из условия:
аsinjmin = 2kl/2.(2)
В промежутках между минимумами наблюдаются максимумы освещенности при углах j, определяемых из условия
аsinjmax = (2k 1)l/2. (3)
Для этих углов фронт MN разбивается на нечетное число зон Френеля z = 2k 1 и одна из зон остается непогашенной. Амплитуда в этом случае будет составлять долю ~ 1/(2k 1), а интенсивность ~ 1/(2k 1)2 от суммарной амплитуды, создаваемой всеми зонами фронта MN.
Центральный максимум будет расположен в точке О против центра щели. По обе стороны от него интенсивность будет спадать до первого минимума, а затем увеличиваться до следующего максимума, см. рисунок. На экране Е будут наблюдаться перемежающиеся светлые и темные полосы с постепенными переходами между ними. Центральная полоса будет наиболее яркой, а освещенность боковых максимумов будет убывать от центра к переферии.
Ширина и число этих полос будут зависеть от отношения l/а. Из (1) видно, что
zmax = a/(l/2). (4)
Если щель очень узкая, а«l, то вся поверхность MN является лишь небольшой частью одной зоны и колебания от всех её точек будут по любому направлению распространяться почти в одинаковой фазе. Условие минимума (2) не может быть выполнено даже для самого меньшего значения k = 1 и во всех точках экрана будет свет. Такая щель является практически точечным источником света, и волна от неё будет распространяется практически одинаково во всех направлениях.
Если щель очень широкая, а»l, то уже первый минимум будет соответствовать очень малому отклонению от прямолинейного распространения света под углом
(j1)min = arcsinla »la <<1. (5)
Следующий минимум будет при угле (j2)min » 2l/a и т.д. В результате прохождения через такую широкую щель плоской волны на экране мы увидим геометрическое изображение щели, окаймлённое по краям тонкими перемеживающимися темными и светлыми полосками.
Чётко выраженные широкие дифракционные максимумы и минимумы будут наблюдаться лишь в промежуточном случае, когда ширина щели всего в несколько раз превышает длину волны и zmax порядка 3-5.
При освещении щели монохроматическим светом дифракционные максимумы для различных цветов разойдутся. Как видно из (3), чем меньше l, тем под меньшими углами расположены дифракционные максимумы.
В центр экрана лучи всех цветов приходят совместно – если щель освещалась белым светом, то изображение в центре также будет белым. Справа и слева от центрального максимума будут наблюдаться дифракционные спектрыпервого, второго и т. д. порядка,обращенные фиолетовым краем к центру, рис.3. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.
длин волн с помощью дифракции на одной щели получить невозможно.
Рис.3. 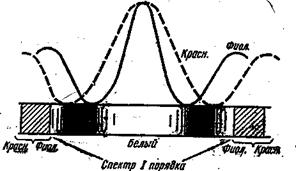
§
Для увеличения интенсивности и более четкого разделения цветов следует воспользоваться не одной щелью, а целой дифракционной решеткой,которая представляет собой ряд параллельных щелей одинаковой ширины а, разделённых между собой непрозрачными промежутками шириной b. Сумма
а b = 1 (1)
называется периодом или постоянной дифракционной решетки.
Конструктивно дифракционная решетка для видимого света изготавливается путем нанесения на прозрачную стеклянную пластинку с помощью алмазного резца делительной машины ряда тонких параллельных штрихов-канавок одинаковой ширины b на равных расстояниях а др. от др. Поверхность стекла внутри канавок становится матовой, и эти канавки являются непрозрачными промежутками, разделяющими участки с ненарушенной поверхностью – “щели”_решётки, 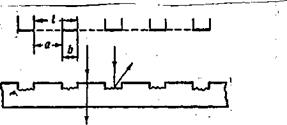 Рис.1.
Рис.1.
Рассмотрим плоскую монохроматическую волну, падающую на решетку, рис.2. Каждая из параллельных щелей решётки дает на экране Е дифракционную картину, показанную на рис.2 пунктиром. Линза L собирает параллельные лучи, идущие от всех щелей под углом Ф
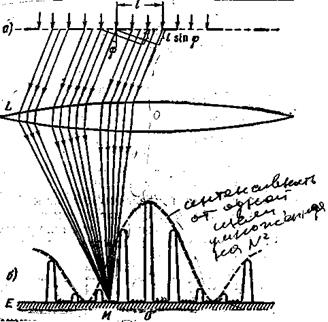
Pис.2.
к главной опт. оси, в одну и ту же точку М фокальной плоскости. При параллельности всех щелей дифракционной решётки и строгой одинаковости их размеров амплитуды колебаний, создаваемых в точке М каждой щелью в отдельности, будут одинаковы. Практически одинаковым будет и распределение вдоль экрана интенсивностей и амплитуд колебаний, приходящих от каждой щели. Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей.
На центральной линии экрана (проходящей через главный фокус линзы О) лучи, идущие от всех щелей, сходятся без дополнительной разности хода, т.е. приходят в одинаковой фазе. При этом их амплитуды просто складываются, и в случае N одинаковых щелей амплитуда суммарного колебания будет в N раз, а интенсивность в N2 раз больше, чем в случае одной щели.
Лучи, идущие от разных щелей под углом j, отличным от нуля, сходятся в точке М, пройдя различные пути и имея различные фазы колебаний; они будут давать при интерференции более сложную картину. Рассмотрим две соседние щели. Из рис.2 видно, что лучи, идущие от соответственных точек обеих щелей (крайних, центральных, промежуточных), имеют одну и ту же разность хода
D = l sinj (2)
и приходят в т. М со сдвигом фазы y = 2p(l sinj)/l. Такой же точно сдвиг фазы y будет между колебаниями, приходящими от третьей щели и второй, четвертой и третьей, и т.д.
Резкое возрастание амплитуды результирующего колебания будет в тех случаях, когда амплитуды колебаний от всех щелей аi направлены одинаково, т.е. имеют сдвиг фазы, целый кратный от 2p, рис.3, что соответствует разности хода между соседними щелями D кратной четному числу полуволн:
lsinjk = 2kl /2 = kl, k = 0, ±1, ±2, ±3, …. (3)
Условие (3) характеризует положение главных максимумов дифракционной решетки. При углах jk, удовлетворяющих (3), А = NА1 и интенсивность дифракционной картины возрастает в К2 раз по ср. с дифракцией от одной щели.
С увеличением N возрастает четкость дифракционной картины – увеличивается интенсивность и уменьшается, ширина главных максимумов. Вследствие интерференции происходит, перераспределение энергии в пространстве, и эта энергия концентрируется, во все более узком интервале углов Djm.
 А
А
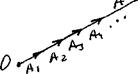
Рис.3.
Подчеркнем, что хотя положение гл. максимумов решетки не зависит от числа щелей, наличие большого числа щелей очень существенно: 1)яркость каждой линии растет как N2, 2) ширина каждой линии убывает как 1/N. Тем самым увеличивается точность производимых измерений.

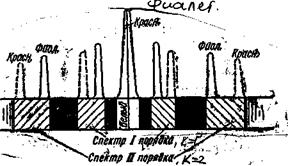 Если на дифракционную решетку будет падать немонохроматический свет, то дифракционные максимумы, для лучей разного цвета пространственно разойдутся. Нулевой макс. (k=0) для всех длин волн будет совпадать при j = 0, но уже максимумы первого порядка (k=1) будут для фиолетовых лучей расположены ближе к центру, чем для красных. Между ними расположатся максимумы промежуточных цветов, и мы будем наблюдать дифракционный спектр первого порядка. Между нулевым и первым порядками расположена практически темная зона очень слабых побочных максимумов. Такая же темная зона расположена между красным концом спектра первого порядка и фиолетовым краем спектра второго порядка, рис.4.
Если на дифракционную решетку будет падать немонохроматический свет, то дифракционные максимумы, для лучей разного цвета пространственно разойдутся. Нулевой макс. (k=0) для всех длин волн будет совпадать при j = 0, но уже максимумы первого порядка (k=1) будут для фиолетовых лучей расположены ближе к центру, чем для красных. Между ними расположатся максимумы промежуточных цветов, и мы будем наблюдать дифракционный спектр первого порядка. Между нулевым и первым порядками расположена практически темная зона очень слабых побочных максимумов. Такая же темная зона расположена между красным концом спектра первого порядка и фиолетовым краем спектра второго порядка, рис.4.
Рис.4.
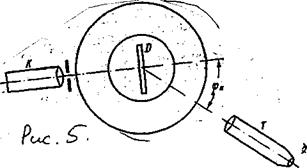
Благодаря узости дифракционных максимумов решетки различные цвета почти не накладываются др. на др. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор (рис.5.).Спектр дифракционной решетки получается тем более четким, чем больше щелей N содержит решетка. Максимальное число наблюдаемых дифракционных спектров определяется из условия, чтобы sinjk <1, т.е.
kmax£ l/l, (4)
Из условия
sinjk =kl/l (5)
видно, что синусы углов в спектре данного порядка прямо пропорциональны длинам волн, т.е. дифракционные спектры, в отличие от призматических, всегда одинаковы и равномерны. Помещая дифракционную решетку D на столик гониометра ( рис.5) и освещая ее пучком параллельных лучей через щель коллиматора К, можно, измеряя угол jk, под которым видны данные лучи в зрительную трубу Т, точно найти их длину волны l.
Дифракционные решетки имеют обычно от 100 до 600 щелей на мм, т.е. период l =10-2 мкм. Лучшие решетки содержат до 1800 щелей на мм, при общей длине до нескольких см., так что общее число щелей достигает 105.
Отражательная решетка изготовляется процарапыванием параллельных штрихов на зеркальной поверхности. Её теория, по существу, не отличается от теории прозрачной решетки.
Для некоторых областей спектра стекло непрозрачно (например, для УФ-лучей). В этом случае нужно пользоваться кварцевой оптикой и отражательными решетками. Без линз можно обойтись, заменяя плоскую отражательную решетку вогнутой.
Основными характеристиками всякого спектрального прибора является его дисперсия и разрешающая сила.Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 1 ангстрем). Разрешающая сила определяет минимальную разность длин волн dl, при которой две линии воспринимаются в спектре раздельно.
Угловой дисперсиейназывается величина
D = djdl, (6)
где dj – угловое расстояние между спектр, линиями, отличающимися на dl (рис.6а). Можно показать, что
D = k/l, (7)
откуда следует, что угловая дисперсия обратно пропорциональна периоду решетки l. Чем выше порядок спектра k, тем больше дисперсия.
Дифракционная решетка

 Линза
Линза
 f j
f j
dj
 dl¢
dl¢
l¢
Рис.6а.
Линейной дисперсиейназывают величину
Dлин = dl¢ /dl, (8)
где dl¢ – линейное расстояние на экране или на фотопластинке между спектр. линиями, отличающимися по длине на dl. Линейная дисперсия связана с угловой дисперсией соотношением
Dлин = fD, (9)
где f – фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Приняв во внимание (7), запишем
Dлин = fk/l, (10)
Разрешающей силойспектрального прибора называют безразмерную величину
R = ldl
где dl – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
Возможность разрешения (т.е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояния между ними (которое определяется дисперсией прибора), но также и от ширины спектрального, максимума (рис. 6). Критерий Рэлея.

Разрешающая сила дифракционной решетки пропорциональна порядку спектра k и числу щелей N, т.е.
Rдифр. реш. = kN.
Современные дифракционные решетки обладают довольно высокой разрешающей силой (до 2×105).
ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА
КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ.
Напомню, что в 1895г Рентген обнаружил, что при электрическом разряде в вакуумной трубке возникает излучение, невидимое для глаза. Дальнейшие исследования показали, что эти лучи, названные рентгеновскими, возникают при бомбардировке вещества быстрыми электронами. В современных рентгеновских трубках мишенью, обстреливаемой электронами , является метал. пластинка -катод, расположенный под углом 45° к потоку электронов. Скорость электронов определяется величиной разности потенциалов между анодом и катодом.
Рентгеновские лучи, предст. собой жесткое электромагнитное излучение, также как и оптическое излучение, обладают волновыми свойствами. Мы уже знаем, что для того, чтобы обнаружить дифракцию, необходимо, чтобы размеры щелей и преград, образующих правильную решетку на пути волн, были не слишком велики по сравнению с длиной волны. Рентгеновские лучи обладают столь малой длиной волны, что на обычных дифракционных решетках для них дифракция не наблюдается.
Проделаем мысленно следующее. Поставим две дифр. решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка даст например в горизонтальном направлении ряд максимумов, положения которых определяются условием
d1 sinj1 = ±m1l(m1 =0, 1,2,3,..,) (1)
Вторая решетка разобьет каждый из образовавшихся т.о. пучков на расположенные по вертикали максимумы, положения которых опр. условием
d2 sinj2 = ±m2l(m2 =0, 1,2,…).
В итоге дифракционная картина будет иметь вид правильно расположенных пятен.
Такая же дифракционная картина получится, если вместо двух разд. решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Подобная пластинка представляет собой двумерную периодическую структуру.
Дифракция наблюдается также на трехмерных структурах, т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако их период (» 10-10 м) слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие d>l выполняется только для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ, Фридриха и Книппинга.
Первые методы расчета дифракции от объемной решетки дал Лауэ.
Совершенно эквивалентные формулам Лауэ, но гораздо более удобные для анализа, формулы были даны независимо русским ученым Вульфом и английскими физиками У .Г. и У.Л .Брэггами. Метод, предложенный ими, состоит в следующем.
Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.1), которые мы будем называть
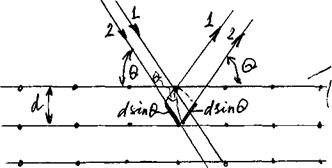
Рис.1.
атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами,
лежащими в таком слое, также будет представлять собой плоскость. Т.о., суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычному закону отражения.
Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различными щелями дифракционной решетки. При этом, как и в случае решетки, вторичные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной l. Из рис.1 видно, что разность хода двух волн, отразившихся от двух соседних слоев, равна 2dsinQ, где d – период идентичности кристалла в направлении, перпендикулярном к рассматриваемым слоям, Q – угол, дополнительный к углу падения и называется углом скольженияпадающих лучей. Следовательно, направления, в которых получаются дифракционные максимумы, определяется условием
2dsinQ = ± ml (m =1,2,…) (1)
Это соотношение называется формулой Вульфа –Брэггов.
Атомные слои в кристалле можно провести множеством способов. Каждая система слоев может дать дифракционный максимум, если для нее окажется выполнимым (1). Однако заметную интенсивность имеют лишь те максимумы, которые получаются за счет отражений от слоев, достаточно густо усеянных атомами. При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти определенный угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться рентгеновским излучением с непрерывным спектром. Тогда для таких условий опыта всегда найдутся длины волн l, удовлетворяющие условию (1).
Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия)и для изучения структуры кристаллов (рентгеноструктурный анализ).
В методе структурного анализа пучок ренг. излучения направляется на кристалл. Для каждой системы слоев, достаточно густо усеянных атомами, находится в излучении длина волны, при которой выполняется условие (1). Поэтому на помещенной за кристаллом фотопластинке получается (после проявления) совокупность черных пятнышек, взаимное расположение которых отражает симметрию кристалла. По расстоянию между пятнышками и по их интенсивности удается найти размещение атомов в кристалле и расстояния между ними.
ПОЛЯРИЗАЦИЯ СВЕТА
ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ. СТЕПЕНЬ ПОЛЯРИЗАЦИИ. ЗАКОН МАЛЮСА.
Напомню, что поляризованным называется свет, в котором направления колебаний светового вектора `Е упорядочены каким-либо образом. В естественном свете колебания разных направлений светового вектора `Е быстро и беспорядочно сменяют друг друга.
Рассмотрим два взаимно перпендикулярных электрических колебания свершающихся вдоль осей х и у и отличающихся по фазе на d (Рис.1):
Еx = A1 coswt, Еy = A2 cos(wt d). (1)
Результирующая напряженность Е является векторной суммой Ех и Еу (рис.1), причем угол j равен
tg j = Е y /Е x = A2 cos(wt d)/ A1 coswt, (2)


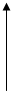 Ey ` E
Ey ` E
 j Ex
j Ex
Рис.1.
Если разность фаз претерпевает случайные хаотические изменения, то и угол j, т.е. направление светового вектора Е, будет испытывать скачкообразные неупорядоченные изменения. В соответствии с этим естественный свет можно представить как наложение двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность. Такое представление намного упрощает рассмотрение прохождения естественного света через поляризационные устройства.
Допустим, что световые волны Ех и Еу когерентны, причем d равно нулю или p. Тогда согласно (2)
tgj = ± А2/А1 = const.
Следовательно, результирующее колебание совершается в фиксированном направлении – волна оказывается плоско поляризованной.
В случае, когда А1 = А2 и d = ±p/2,
tgj = ± tgwt
т.к. (соs(wt±л/2) = ±sinwt). Отсюда вытекает, что плоскость колебаний поворачивается вокруг направления луча с угловой скоростью, равной частоте колебания w. В этом случае свет 6удет поляризованным по кругу.
В случае произвольного постоянного d в результате сложения двух взаимно перпендикулярных колебаний получим вектор Ё, конец которого движется по эллипсу (в частном случае, может получиться движение по прямой или по окружности), т.е. мы получаем в результате сложения таких волн эллиптически поляризованную световую волну. При разности фаз d=0 или d=p, эллипс вырождается в прямую и получается плоско поляризованный свет. При d = ±p/2 и равенстве амплитуд складываемых волн эллипс превращается в окружность – получается свет поляризованный по кругу.
В зависимости от направления вращения вектора Е различают правую и левую эллиптическую и круговую поляризацию.Если по отношению к направлению, противоположному направлению луча, вектор Е вращается по часовой стрелке, поляризация называется правой, в противоположном случае – левой.
Плоскость, в которой колеблется световой вектор в плоско поляризованной волне, называется плоскостью колебаний. Плоскостью поляризацииназывается не плоскость, в которой колеблется вектор Е, а перпендикулярная к ней плоскость.
Плоско поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами.Эти приборы свободно пропускают колебания, параллельные плоскости, которую мы будем называть плоскостью поляризатора,и полностью или частично задерживают колебания, перпендикулярные к этой плоскости. Поляризатор, задерживающий перпендикулярные к его плоскости колебания только частично, называется несовершенным.Просто поляризатором мы будем для краткости называть идеальный поляризатор, полностью задерживающий колебания, перпендикулярные к его плоскости, и не ослабляющий колебаний, параллельных плоскости. Поляризатор представляет собой среду, структура и свойства которой в различных направлениях, перпендикулярных лучу, различны, т.е. эта среда анизотропна. Такими средами для света являются преимущественно кристаллические тела с невысокой степенью симметричности.
На выходе из несовершенного поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями других направлений. Такой свет называется частично поляризованным. Его можно рассматривать как смесь естественного и плоско поляризованного. Частично поляризованный свет, как и естественный, можно представить в виде наложения двух некогерентных плоско поляризованных волн с взаимно перпендикулярными плоскостями колебаний. Отличие заключается в том, что в случае естественного света интенсивность этих волн одинакова, а в случае частично поляризованного – разная.
Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от Imax до Imin, причем переход от одного из этих значений к другому будет совершаться при повороте на угол, равный p/2 (за один полный оборот два раза будет достигаться макс, и два раза мин. значение интенсивности). Величина
P = (Imax – Imin)/( Imax Imin)(3)
называется степенью поляризации. Для плоско поляризованного света Imin = 0 и Р=1; для естественного света Imax = Imin и Р = 0. Т.е. любой естественный луч света не поляризован. К эллиптически поляризованному свету понятие степени поляризации не применимо (у такого света колебания вектора напряженности электрического поля полностью упорядочены, так что степень поляризации всегда равна единице).
Пусть на поляризатор падает плоско поляризованный свет амплитуды а0 и интенсивности I0. Сквозь поляризатор пройдет составляющая колебания с амплитудой А = а0 соsj, где j- угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением
I = I 0 соsj. – закон Малюса. (4)
Поставим на пути естественного луча два поляризатора, плоскости которых образуют угол j. Из первого поляризатора выйдет плоско поляризованный свет, интенсивность которого I 0 составляет половину интенсивности естественного света. Согласно закону Малюса из второго поляризатора выйдет свет интенсивности I 0 соs2j. Т.о., интенсивность света, прошедшего через два поляризатора, равна
I = (Iестcos2j)/2.(5)
Максимальная, интенсивность, равная (1/2)Iест получается при j=0 (поляризаторы параллельны). При j = p/2 интенсивность равна нулю – скрещенные поляризаторы света не пропускают.
В случае света, поляризованного по кругу, вращение поляризатора не сопровождается (как и в случае естественного света) изменением интенсивности света, прошедшего через поляризатор.
§
Если угол падения естественного света на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) отличен от нуля, отраженный и преломлённый лучи оказываются частично поляризованными. В отражённом луче преобладают колебания, перпендикулярные кплоскости падения (на рис.1 эти колебания обозначены точками), в преломлённом луче – колебания, параллельные плоскости падения (на рис.1они изображены двусторонними стрелками). Степень поляризации зависит от угла падения.
Рис.1.
Обозначим через QБр угол, удовлетворяющий условию
QБр = n12 (1)
n12 – показатель преломления второй среды относительно первой. При угле падения Q= QБр (на рис. QБр =IB) отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном углу Брюстера, достигает наибольшего значения, однако этот луч остается поляризованный только частично.
Соотношение (1) носит название закона Брюстера,а угол QБр называется углом Брюстера.При падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.
При прохождении света через все прозрачные кристаллы, за исключением принадлежащих к кубической системе, наблюдается явление, получившее название двойного лучепреломления.Это явление заключается в том, что упавший на кристалл луч естественного света разделяется внутри кристалла на два луча, распространяющиеся, вообще говоря, с разными скоростями и в различных направлениях
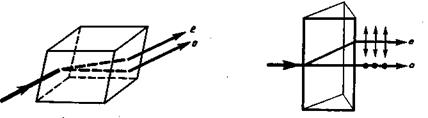
Рис.2.
Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные и двуосные.У одноосных кристаллов один из преломленных лучей подчиняется обычному закону преломления, в частности он лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности, этот луч называется обыкновенными обозначается буквой о. Для другого луча, называемого необыкновенным(его обозначают буквой е), отношение синусов угла падения и угла преломления, не остается постоянным при изменении угла падения. Даже при нормальном падении света на кристалл необыкновенный луч, вообще говоря, отклоняется от нормали, рис.2. Кроме того, необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Примерами одноосных кристаллов могут служить исландский шпат, кварц ятурмалин. У двуосных кристаллов (сдюда, гипс) оба луча необыкновенные- показатели преломления для них зависят от направления в кристалле. У одноосных кристаллов имеется направление, вдоль которого обыкновенный и необыкновенный лучи распространяются не разделяясь и с одинаковой скоростью. У двуосных кристаллов имеется два таких направления. Такие направления в кристалле называются оптической осью кристалла. Оптическая ось – это определенное направление в кристалле и любая прямая, параллельная данному направлению, является оптической осью.
Любая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла.Обычно пользуются главным сечением, проходящим через световой луч.
Исследования обыкновенного и необыкновенного лучей показали, что обалуча полностью поляризованы во взаимно перпендикулярных, направлениях(рис.2). Плоскость колебаний обыкновенного луча перпендикуляра к главному сечению кристалла. В необыкновенном луче колебания светового вектора совершаются в плоскости, совпадающей с главным сечением. По выходе из кристалла оба луча отличаются др. от др. только направлением поляризации, так что названия “обыкновенный” и “необыкновенный” лучи имеют смысл только внутри кристалла.
В некоторых кристаллах один из лучей поглощается сильнее другого. Это явление называется дихроизмом.Очень сильным дихроизмом в видимых лучах обладает турмалин,в котором обыкновенный луч практически полностью поглощается на длине 1мм. В кристаллах сульфата йодистого хининаодин из лучей поглощается на пути примерно в 0,1мм. Это обстоятельство используется для изготовления поляризационного устройства, называемого поляроидом.Оно представляет собой целлулоидную пленку, в которую введено большое количество одинаково ориентированных кристаллов сульфата йодистого хинина.
Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы диэлектрическая проницаемость e оказывается зависящей от направления. В одноосных кристаллах e в направлении оптической оси и в направлениях, перпендикулярных к ней имеет различные значения eêê и e^. В других направлениях e имеет промежуточные значения. Поскольку n = Öe, следовательно, из анизотропии e вытекает, что электромагнитным волнам с различными направлениями колебаний вектора Ё соответствуют разные значения n. Поэтому скорость световых волн зависит от направления колебаний светового вектора `Е.
Одноосные кристаллы характеризуются показателем преломления обыкновенного луча,равным n0 = c/V0, и показатель преломления необыкновенного луча, перпендикулярного к оптической оси, равным ne = с/Vе. Последнюю величину называют просто показателем преломления необыкновенного луча.
В зависимости от того, какая из скоростей больше, различают положительные и отрицательные одноосные кристаллы.У положительных кристаллов Vе меньше V0 (это значит ne> n0).
Ход обыкновенного и необыкновенного лучей в кристалле можно определить с помощью принципа Гюйгенса.
§
В прозрачных аморфных телах, а также в кристаллах кубической системы может возникать двойное лучепреломление под влиянием внешних воздействий. В частности, это происходит при механических деформациях тел. Мерой возникающей оптической анизотропии служит разность показателей преломления обыкновенного и необыкновенного лучей. Опыт показывает, что эта разность пропорциональна механическому напряжению s в данной точке тела:
n0 – ne = ks (1)
(k- коэффициент пропорциональности, зависящий от свойств вещества).
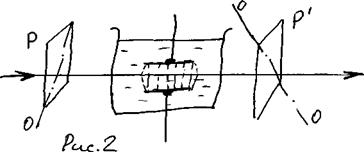 Поместим стеклянную, пластинку Q между скрещенными поляризаторами Р1 и Р2. (рис.1).
Поместим стеклянную, пластинку Q между скрещенными поляризаторами Р1 и Р2. (рис.1).


 P1 Q P2
P1 Q P2
 F
F
Рис.1.
Пока стекло не деформировано, такая система света не пропускает. Если же пластинку подвергнуть сжатию, свет через систему начнет проходить, причем наблюдаемая в прошедших лучах картина оказывается испещренной цветными полосами. Каждая такая полоса соответствует одинаково деформированным местам пластинки. Следовательно, по расположению полос можно судить о распределении напряжений внутри пластинки. На этом основан метод исследования напряжений. Изготовленная из прозрачного изотропного материала (например, из плексиглаза) модель какой-либо детали или конструкции помещается между скрещенными поляризаторами. Модель подвергается действию нагрузок, подобных тем, какие будет испытывать само изделие. Наблюдаемая при этом в проходящем свете картина позволяет определить распределение напряжений, а также судить об их величине.
Возникновение двойного лучепреломления в жидкостях и в аморфных твердых телах под воздействием электрического поля было обнаружено Керром в 1875г. Это явление получило назв. эффекта Керра.В 1930г. этот эффект был обнаружен и в газах.
Схема установки для исследования эффекта Керра в жидкостях (рис.2) сост. из ячейки Керра,помещенной между скрещенными поляризаторами Р и Р’. Ячейка Керра представляет собой герметичный сосуд с жидкостью, в которую введены пластины конденсатора. При подаче на пластины напряжения между ними возникает практически однородное электрическое поле. Под его действием жидкость приобретает свойства одноосного кристалла с оптической осью, ориентированной вдоль поля.
Возникающая разность показателей преломления
n0 – ne = kE2 (2)
На пути l между обыкновенным и необыкновенным лучами возникает разность хода
D = (n0 – ne )l = klE2
или разность фаз
d = (Dl0)2p = 2pklE2/l0. (3)
Это выражение принято записывать в виде
d =2pВl Е2, (4)
где В – характерная для вещества величина, называется постоянной Керра.
Из известных жидкостей наибольшей постоянной Керра обладает нитробензол. Постоянная Керра зависит от Т и от l.
Эффект Керра объясняется различной поляризуемостью молекул по разным направлениям. В отсутствии поля молекулы ориентированы хаотическим образом, поэтому жидкость в целом не обнаруживает анизотропии. Под действием поля молекулы поворачиваются так, чтобы в направлении поля были ориентированы либо их дипольные электрические моменты (у полярных молекул), либо направления наибольшей поляризуемости (у неполярных молекул). В результате жидкость становится оптически анизотропной. Ориентирующему действию поля противится тепловое движение молекул. Этим обусловлено уменьшение пост. Керра с повышением Т.
Время, в течение которого устанавливается (при включении поля) или исчезает (при выключении электрического поля) преимущественная ориентация молекул, составляет около 10-10 с. Поэтому ячейка Керра, помещенная между скрещенными поляризаторами, может служить практически безынерционным затвором. В отсутствии напряжения на пластинах конденсатора затвор будет закрыт. При включении напряжения, затвор пропускает значительную часть света, падающего на первый поляризатор (рис.2).
Естественное вращение. Некоторые вещества, называемые оптически активными,обладают способностью вызывать вращение плоскости поляризации проходящего через них плоско поляризованного света. К числу таких веществ принадлежат кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты и др.).
Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла. Угол поворота j пропорционален пути l, пройденному лучом в кристалле:
j = al. (5)
Коэф, a называется постоянной вращения.Эта постоянная зависит от длины волны (дисперсия вращательной способности).
В растворах угол поворота плоскости поляризации пропорционален пути света в растворе и концентрации активного вещества с;
j = gс l.(6)
где g – удельная постоянная вращения.
В зависимости от направления вращения плоскости поляризации оптически активные вещества подразделяются, на право- и левовращающие.Направление вращения не зависит от направления луча. Все оптически активные вещества существуют в двух разновидностях – правовращающей и левовращающей. Существует право- и левовращающий кварц, право- и левовращающий сахар и т.д. Молекулы или кристаллы одной разновидности являются зеркальным отражением молекул или кристаллов другой разновидности,
Рис.3.
Буквами обозначены отличающиеся др. от др. атомы или группы атомов (радикалы). Молекула б является зеркальным отражением молекулы а.
Если между двумя скрещенными поляризаторами поместить оптически активное вещество (кристалл кварца, прозрачную кювету с раствором сахара и т.п.), то поле зрения просветляется. Чтобы снова получить темноту, нужно повернуть один из поляризаторов на угол j, определяемый выражением (5) или (6), и можно определить концентрацию раствора с. Такой способ определения концентрации применяется в производстве различных веществ, в частности, в сахароварении (прибор называется сахариметром).
Магнитное вращение плоскости поляризации. Оптически неактивные вещества приобретают способность вращать плоскость поляризации под действием МП. Это явление было обнаружено Фарадеем и называется иногда эффектом Фарадой.Оно наблюдается только при распространении света вдоль направления намагниченности. Поэтому для наблюдения эф. Фарадея в полюсных наконечниках просверливают отверстия, через которые пропускают световой луч. Исследуемое вещество помещается между полюсами магнита.
Угол поворота плоскости поляризации j пропорционален пути l, проходимому светом в веществе, и намагниченности вещества. Намагниченность в свою очередь пропорциональна напряженности магнитного поля Н. Поэтому
j = VlH (7)
Коэффициент V называется постоянной Верде или удельным магнитным вращением.Постоянная V, как и постоянная вращения a, зависит от длины волны.
Направление вращения определяется направлением магнитного поля. От направления светового луча знак вращения плоскости поляризации не зависит. Поэтому, если, отразив луч зеркалом, заставить его пройти через намагниченное вещество ещё раз в обратном направлении, поворот плоскости поляризации удвоится.
Магнитное вращение плоскости поляризации обусловлено возникающей под действием магнитного поля прецессией электронных орбит.
Оптически активные вещества под действием магнитного поля приобретают дополнительную способность вращать плоскость поляризации, которая складывается с их естественной способностью.
Поток вектора напряженности электрического поля
Из рис. 1.2.2 видно, что густота силовых линий может служить и количественным показателем величины E . Для этого необходимо, чтобы число силовых линий, пересекающих единичную площадку, нормальную к вектору напряженности, было равно модулю вектора напряженности Е .
1.2.2. Поток вектора напряженности
Если силовые линии однородного электрического поля напряженностью E пронизывают некоторую площадку S, то поток вектора напряженности будет определяться формулой
…
где En – произведение вектора E на нормаль n к данной площадке (рис. 1.2.3).
Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности ФЕ через эту поверхность.
В векторной форме можно записать, что ФЕ = (E, S) – скалярное
произведение двух векторов, где вектор S = nS.
Таким образом, поток вектора E есть скаляр, который в зависимости от величины угла а может быть как положительным, так и отрицательным. Рассмотрим примеры, изображенные на рис. 1.2.4 и 1.2.5.
§
1.2. Теорема Остроградского-Гаусса
1.2.1. Силовые линии электростатического поля
Для того чтобы описать электрическое поле, нужно задать вектор напряженности в каждой точке поля. Это можно сделать аналитически или графически. Для этого пользуются силовыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности E (рис. 1.2.1).
Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
Рассмотрим случай однородного электрического поля.
Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению, т.е. E = const.
Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга. Такое поле можно создать между заряженными бесконечными параллельными пластинами, например между пластинами конденсатора (рис. 1.2.2).
Поле точечного заряда неоднородно. Для точечного заряда линии напряженности исходят из положительного заряда и уходят в бесконечность и из бесконечности входят в отрицательный заряд. Так как Е ~ 1/r2, то и густота силовых линий обратно пропорциональна квадрату расстояния от заряда. Так как площадь поверхности сферы, через которую проходят эти линии, сама возрастает пропорционально квадрату расстояния, то общее число линий остается постоянным на любом расстоянии от заряда.
Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному (рис. 1.2.2).
§
Контрольные вопросы
1. В чем заключается закон сохранения заряда? Приведите примеры проявления закона.
2. Сформулируйте четыре закона сохранения существующих в природе.
3. Что представляет собой электростатическое поле и как его можно изобразить графически?
4. Запишите, сформулируйте и объясните закон Кулона.
5. Какие поля называют электростатическими?
6. Что такое напряженность E электростатического поля?
7. Каково направление вектора напряженности E ? Единица напряженности в СИ.
8. Какая физическая величина является силовой характеристикой электростатического поля? Напишите ее формулу.
9. Что такое поток вектора E ? Единица его в СИ?
10. Электрический диполь помещен внутрь замкнутой поверхности. Каков поток ФЕ сквозь эту поверхность?
11. Пользуясь принципом суперпозиции, найдите в поле двух точечных зарядов q и 2q, находящихся на расстоянии l друг от друга, точку, где напряженность поля равна нулю.
12. Чему равно отношение напряженностей электростатических полей в точке В, лежащей на продолжении оси диполя (рис. 1.1.2), и в точке А, лежащей на перпендикуляре, проходящем через середину О оси этого диполя, если ОА= ОВ?
13. Приведите формулу напряженности в точке С расположенной произвольно по отношению к диполю.
14. Два одинаковых шарика, имеющих заряды по 400 нКл соединены пружиной и находятся на гладком горизонтальном столе. Шарики колеблются так, что расстояние между ними меняется от L до 4L. Найдите жесткость пружины, если известно, что ее длина в свободном состоянии 2L, где L = 2 см.
15. Два небольших тела массой 5 г каждое, заряженные одинаковым зарядом 1 мкКл, находятся на горизонтальной плоскости на расстоянии 10 м друг от друга. Коэффициент трения тел о плоскость равен 0,5. Какую минимальную начальную скорость надо сообщить одному из тел, чтобы сдвинуть с места второе тело?
16. В поле силы тяжести закреплен точечный заряд -10 мкКл, а под ним на расстоянии 5 м находится частица массой 9 г и зарядом 4 мкКл. Какую минимальную вертикальную скорость (в единицах СИ) надо сообщить частице, чтобы она долетела до закрепленного заряда?
§
Здесь l называют плечо диполя – вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.
Пример 1. Найдем … в точке А, лежащей на прямой, проходящей через центр диполя и перпендикулярной к оси диполя (рис. 1.1.2):
…
Из подобия заштрихованных треугольников можно записать:
…
Обозначим вектор: p = ql – электрический момент диполя (или дипольный момент), это произведение положительного заряда диполя на плечо l. Направление p совпадает с направлением l, т.е. от отрицательного заряда к положительному. Тогда, учитывая что ql = p, получим
…
Пример 2. На оси диполя, в точке В (рис. 1.1.2),
…
Пример 3. В произвольной точке …:
…
Из приведенных примеров видно, что напряженность электрического поля системы зарядов равна геометрической сумме напряженностей полей каждого из зарядов в отдельности (принцип суперпозиции).
§
1.1.4. Сложение электростатических полей. Принцип суперпозиции
Одним из фундаментальных принципов физики является принцип независимости действия сил, или принцип суперпозиции, который распространяется и на электростатику.
Если поле создается несколькими точечными зарядами, то на пробный заряд q действует со стороны заряда такая сила, как если бы
других зарядов не было.
…
Результирующая сила определится выражением:
…
– это математическая формулировка принципа суперпозиции.
Так как F = qE ,то E – результирующая напряженность поля
в точке, где расположен пробный заряд; так же подчиняется принципу суперпозиции:
…
Напряженность результирующего поля системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из них в отдельности.
1.1.5. Электростатическое поле диполя
Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов, расстояние между которыми l значительно меньше расстояния до точек, где определяется поле системы, т. е. r >> l (рис. 1.1.2)
§
ВВЕДЕНИЕ
Во второй части пособия рассмотрены вопросы электростатики, классической электродинамики и электромагнитные колебания и волны, включая экспериментальные законы и общую теорию методов. Возможно, это самый важный раздел физики, поскольку электромагнитные взаимодействия не только объясняют все электрические и магнитные явления, но и обеспечивают силы, благодаря которым вещество на атомном и молекулярном уровне существует как целое. Изучение электромагнитных взаимодействий на основе квантовой механики позволяет объяснить существование и свойства атомов, молекул и твердых тел.
Цель пособия – помочь студентам освоить материал программы, научить активно применять теоретические основы физики как рабочий аппарат, позволяющий решать конкретные задачи.
Пособие ориентировано на организацию самостоятельной работы студентов. Для удобства работы в приложении приведены фундаментальные физические константы, таблицы физических величин, некоторые справочные данные и сведения о размерностях физических величин. Более точные значения физических постоянных и таблицы физических величин приведены в справочнике «Фундаментальные константы. Таблицы физических величин».
Знание законов электромагнетизма играет огромную роль в решении большого количества проблем современной науки и техники и определяет развитие энергетики, транспорта, вычислительной техники, физики плазмы, термоядерного синтеза и т.д. Дефектоскопия, электромагнитные линзы, магнитная запись информации, поезда на магнитной подушке – вот далеко не полный перечень перспективных областей промышленного применения электромагнитного поля. В течение многих лет не ослабевает интерес к электромагнитным полям биологических объектов, повышено внимание к среде их обитания.
§
1.1. ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
1.1. Электростатическое поле в вакууме
1.1.1. Электрический заряд. Закон сохранения электрического заряда
Электростатика – раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля.
Перемещение зарядов либо отсутствует, либо происходит так медленно, что возникающие при движении зарядов магнитные поля ничтожны. Сила взаимодействия между зарядами определяется только их взаимным расположением. Следовательно, энергия электростатического взаимодействия – потенциальная энергия.
Несмотря на обилие различных веществ в природе существуют только два вида электрических зарядов: заряды подобные тем, которые возникают на стекле, потертом о шелк, и заряды, подобные тем, которые появляются на янтаре, потертом о мех. Первые были названы положительными, вторые – отрицательными зарядами. Так их назвал американский ученый Бенджамин Франклин в 1746 г. Одним из фундаментальных законов природы является закон сохранения электрического заряда: алгебраическая сумма зарядов замкнутой системы сохраняется при любых процессах, проходящих внутри этой системы.
Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов и др.
Опытным путем в 1914 г. американский физик Р. Милликен показал, что электрический заряд дискретен. Заряд любого тела составляет целое кратное от элементарного электрического заряда e = 1,6 • 10-19 Кл:
q = ±ne,
где n – целое число.
Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
1.1.2. Взаимодействие электрических зарядов в вакууме. Закон Кулона
Точечным зарядом (q) называется заряженное тело, размеры которого пренебрежительно малы по сравнению с расстоянием до других заряженных тел, с которым оно взаимодействует.








