- В единицах си
- Измерение магнитного потока
- Конвертер напряжённости электрического поля • электротехника • определения единиц • онлайн-конвертеры единиц измерения
- Магнитная индукция и магнитные поток
- Напряженность точечного заряда в вакууме
- Напряжённость электрического поля произвольного распределения зарядов
- Общие сведения
- Примечания
- Сила, с которой электромагнитное поле действует на заряженные частицы
- Уравнения максвелла
- Электростатика
В единицах си
Для точечного заряда в электростатике верен закон Кулона
- φ=14πε0⋅qr,{displaystyle varphi ={frac {1}{4pi varepsilon _{0}}}cdot {frac ?{r}},}
или
- E→=14πε0⋅qr2⋅r→r,{displaystyle {vec {E}}={frac {1}{4pi varepsilon _{0}}}cdot {frac ?{r^{2}}}cdot {frac {vec {r}}{r}},}
- E≡|E→|=14πε0⋅qr2.{displaystyle Eequiv |{vec {E}}|={frac {1}{4pi varepsilon _{0}}}cdot {frac ?{r^{2}}}.}
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего, исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S{displaystyle S} в виде сферы с центром в точечном заряде, учесть, что направление E→{displaystyle {vec {E}}} будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E{displaystyle E} можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r{displaystyle r}: 4πr2{displaystyle 4pi r^{2}}, имеем:
- 4πr2E=q/ε0,{displaystyle 4pi r^{2}E=q/varepsilon _{0},}
откуда сразу получаем ответ для E{displaystyle E}.
Ответ для φ{displaystyle varphi } получается интегрированием E{displaystyle E}:
- φ=−∫E→⋅dl→=−∫Edr.{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}=-int E,dr.}
Измерение магнитного потока
Устройство, используемое для измерения магнитного потока, называется флюксметром. Принцип действия флюксметра основан на законе магнитной индукции в интегральной форме. Первые флюксметры были механическими. Классический флюксметр представлял собой разновидность баллистического гальванометра, в котором управляющий момент был очень мал, в то время как электродинамическое демпфирование — очень большим.
Подвеска измерительной рамки прибора была устроена таким образом, что возвращающая сила была равна нулю. Измерительная катушка помещалась в изменяющееся магнитное поле и флюксметр определял изменение напряжения в катушке, которое было пропорциональным скорости изменения магнитного потока.
Интегрирование осуществлялось механически за счет высокой инерционности прибора. Именно таким флюксметром пользовался Вильгельм Эдуард Вебер во время исследования направления магнитного поля Земли. Аналогичные флюксметры использовались и на флоте для измерения магнитного поля кораблей с целью контроля их размагничивания.
Современный флюксметр состоит из измерительных катушек и электроники, которая оценивает изменение напряжения в катушке с последующим его интегрированием, рассчитывая таким образом магнитный поток. Для измерения магнитного потока необходимо интегрирование напряжения измерительной катушки в течение времени измерения.
Такое интегрирование напряжения, снятого с измерительной катушки, осуществляется либо с помощью аналогового интегратора (обычно используется интегрирующий операционный усилитель), либо с помощью аналого-цифрового интегратора или микропроцессора, осуществляющего численное интегрирование.
Измерительная катушка флюксметра может быть стационарной или подвижной. Для получения надежных результатов важно, чтобы каркас катушки имел хорошую механическую жесткость и малый коэффициент теплового расширения. Высокую стабильность и повторяемость результатов обеспечивает правильная намотка катушки.
Используемые в электронных флюксметрах катушки бывают точечными, линейными, плоскостными и катушками для измерения гармонических составляющих. Все катушки должны быть откалиброваны, так как основной вклад в погрешность измерений вносят именно катушки с неправильно определенной чувствительностью. Для калибровки катушек применяют постоянные магниты с известными свойствами.
Точечные катушки используются для измерения магнитного потока в определенной точке пространства. Они обычно наматываются на небольшом сердечнике. Такие катушки часто имеют форму шара. Линейные катушки предназначены для измерения интегрированного магнитного потока вдоль прямой линии.
Их ширина намного меньше длины. Линейные катушки обычно охватывают лишь небольшую зону измеряемого пространства. Плоскостные катушки предназначены для измерения больших зон измеряемого пространства. Длинные прямоугольные катушки часто используются при измерениях в ускорителях элементарных частиц.
Для измерения изменения магнитного потока с помощью одной или нескольких измерительных катушек используют различные методы. При измерении катушку могут перемещать из зоны, где имеется поле, в зону, где поле нулевое. Другим методом является отключение поля в процессе измерения. При использовании еще одного метода катушку поворачивают и измерение повторяют.
Для измерения с помощью электронного флюксметра, например, магнитного потока постоянного магнита для контроля качества в процессе производства магнитов, выполняется приведенная ниже последовательность действий.
- К входу флюксметра подключается измерительная катушка.
- После включения прибора и выбора диапазона измерений выполняется контроль уровня дрейфа. Обычно из-за дрейфа нулевые показания поддерживаются не более нескольких минут, после чего нужно заново настраивать прибор.
- Положительное измерение. При пустой измерительной катушке нажать кнопку сброса, затем поместить в катушку магнит так, чтобы его северный полюс был вверху. Записать измеренное значение.
- Отрицательное измерение. Вначале поместить магнит в измерительную катушку северным полюсом вверх. Нажать кнопку сброса, извлечь магнит из катушки и отнести на достаточно большое расстояние от нее. Считать и записать измеренное значение.
- Рассчитать среднее значение двух измерений.
- Магнитная пленка-визуализатор позволяет наблюдать стационарные или медленно меняющиеся магнитные поля
Конвертер напряжённости электрического поля • электротехника • определения единиц • онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Определения единиц конвертера «Конвертер напряжённости электрического поля» на русском и английском языках
Преобразовать единицы с помощью конвертера «Конвертер напряжённости электрического поля»
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Магнитная индукция и магнитные поток
Напряженность магнитного поля не является основной величиной, характеризующей магнитное поле, хотя определение напряжённости действительно для расчёта катушек без магнитопровода.
Для катушки с магнитопроводом основной величиной характеризующей магнитное поле, является магнитная индукция В. Это векторная величина, т.е. она (как и напряженность) задаётся численным значением и направлением в пространстве. Магнитная индукция определяется по силе, действующей на движущуюся заряженную частицу. При изображении картины магнитного поля при помощи магнитных линий, их рисуют гуще в той части поля, где больше индукция.
Единицей измерения магнитной индукции является тесла (Тл). Ранее применялась другая единица измерения магнитной индукции – гаусс (Гс).
Эти единицы связаны соотношением: 1Тл = 10000Гс.
Произведение магнитной индукции В на площадь S, перпендикулярную вектору магнитной индукции (магнитным линиям), называется магнитным потоком Ф. Таким образом магнитный поток:
Ф = B*S
Единицей измерения магнитного потока является вебер (Вб). При одной и той же напряжённости магнитного поля Н, в разных материалах получаются различные магнитные индукции В. Отношение В/Н называется абсолютной магнитной проницаемостью материала μа, т.е.
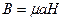
Абсолютная магнитная проницаемость материала μа равна произведению магнитной постоянной (магнитной проницаемости вакуума) μ0 и относительной магнитной проницаемости μr:
раоорропор
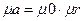
 Магнитная постоянная
Магнитная постоянная
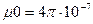 Гн/м (генри на метр, генри единица измерения индуктивности).
Гн/м (генри на метр, генри единица измерения индуктивности).
Величина μr показывает, во сколько раз μа материала больше, чем магнитная постоянная μ0.
В материале, магнитная проницаемость которого равна μr,

а в вакууме (практически и в воздухе)

где В выражается в теслах, а Н в А/м.
При измерении магнитной индукции в гауссах, а напряжённости магнитного поля в А/см, для магнитной индукции в воздухе получим:

У ферромагнитных материалов относительная магнитная проницаемость μr во много раз больше 1, она изменяется с изменением индукции В. Зависимость между В и Н для ферромагнитных материалов чаще изображается графиком в виде кривых намагничивания.
В практических задачах (магнитные цепи электрических машин и аппаратов) для расчёта силы тяги, ЭДС, силы притяжения и т.д. требуется определить магнитный поток Ф или индукцию В. Значение этих величин определяют по кривым намагничивания, если известна напряженность магнитного поля Н, которая, в свою очередь, задаётся магнитным напряжением или МДС.
Задача 1.
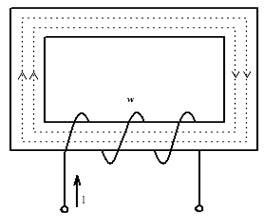 Напряжённость магнитного поля катушки
Напряжённость магнитного поля катушки
H = 500 А/м. Какова будет магнитная индукция, если в катушку вставить магнитопровод из трансформаторной стали (на рис.), относительная магнитная проницаемость которой μr = 2400.
Решение
B = μа*Н = μо*μr*Н = 4*π*10-7*2400*500 = 1.5 Тл
Задача 2.
Для трансформаторной стали, содержащей 4% Si, магнитная индукция В при напряжённости магнитного поля катушки 500 А/м равна 1.19 Тл (см. кривые намагничивания на рис.). Определить абсолютную магнитную проницаемость трансформаторной стали в рабочей точке μа и относительную магнитную проницаемость μr. Напомним, что величина μr показывает во сколько раз μа материала больше, чем магнитная проницаемость
μо = 4*π*10-7.
Решение
Абсолютная магнитная проницаемость
μа = В/Н = 1.19/500
μа = μr*μо = 4*π*10-7*μr.
Отсюда
μr = μа/μо = В/Н =1.19/(500*4*π*10-7) = 1893.9
Задача 3.
По заданным экспериментальным зависимостям В и Н для различных материалов определить коэффициенты полиномов второго порядка, наилучшим способом (по минимуму суммы квадратов ошибок) обеспечивающих аналитическое их описание (математическую модель).
Листовая сталь
| Н (А/м) | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 |
| В (Тл) | 0.60 | 0.75 | 0.86 | 0.96 | 1.05 | 1.12 | 1.19 | 1.23 | 1.30 | 1.36 |
Трансформаторная сталь (4% Si)
| Н (А/м) | 100 | 200 | 300 | 400 | 500 | 600 |
| В (Тл) | 0.48 | 0.78 | 0.96 | 1.08 | 1.19 | 1.27 |
Литая сталь
| Н (А/м) | 100 | 200 | 300 | 400 | 500 | 600 |
| В (Тл) | 0.35 | 0.60 | 0.85 | 1.00 | 1.10 | 1.16 |
Решение
Для оценки коэффициентов полинома
В = a*Н2 b*Н С
Запишем вектор
Н = [100 150 200 250 300 350 400 450 500 550]’. size A = 10,1
Затем составим матрицу А:
А = [Н^2 Н ones(V(1),1)]
И образуем вектор В:
B = [0.6 0.75 0.86 0.96 1.05 1.12 1.19 1.23 1.3 1.36]’.
Выполним оценку коэффициентов
а х = АВ
С помощью файла sah575.m. В нём выполнены оценки коэффициентов квадратного полинома для листовой стали
а1 = [-0.0206 0.2952 0.3429],
для трансформаторной стали
а2 = [-0.0246 0.3239 0.2000]
и для листовой стали
а3 = [-0.0277 0.2566 0.0150].
Необходимо выполнить расчёты для каждого вида материала в режиме прямых вычислений.
/здесь приводится файл sah 375.m/
Задача 4.
Каков будет магнитный поток Ф в магнитопроводе (см. задачу 1.), если сечение магнитопровода S = 4 см²?
Решение
Магнитный поток, измеряемый в веберах (Вб), равен
Ф = В*S = 1.5*4*10-4 = 0.0006 Вб
(Тл = Вб/м²)
Задача 5.
Число витков катушки w =500. В магнитопроводе из трансформаторной стали длиной l =25 см необходимо обеспечить магнитную индукцию В=1.19 Тл. Какая м.д.с. и ток необходим для этого?
Решение
По кривой намагничивания трансформаторной стали (см. рис.) находим, что для создания В = 1.19 Тл требуется создать напряжённость магнитного поля Н = 500 А/м. При длине магнитопровода (с катушкой) l = 25 см = 0.25 м необходимая м.д.с. вычисляется по формуле
I*w = H*l = 500 А/м * 0.25 м = 125 А,
Отсюда I = I*w/w = 125/500 = 0.25 А
Задача 6.
Каковы напряжённость, индукция и магнитный поток внутри цилиндрической катушки (рис.) которая имеет длину 20 см, диаметр 3см, число витков 1600 и ток 3 А?
Решение
Напряжённость магнитного поля
Н = I*w/l = 3*1600/0.2 = 24000 А/м
Поскольку катушка без сердечника, то магнитную индукцию следует вычислять по формуле:
В = μо*Н = 4*π*10-7*2.4*104 = 3.02*10-2 Тл
Сечение катушки
S = π*d2/4 = 3.14*0.032/4 = 7.06*10-4 м².
Следовательно, магнитный поток
Ф = В*S = 3.02*10-2*7.06*10-4 = 21.3*10-6 Вб

Дополнение
Задача 1
Какое количество электричества пройдёт через лампу за 3 часа при токе 0,18А?
Решение:

Задача 2
Свинцовый аккумулятор ёмкостью 14А*ч заряжается током I зар = 1.4А. Как долго он должен заряжаться и через сколько времени он разрядится через лампы током Iраз = 0.3А?
Решение:
Зарядка: t = Q/Iзар = 14А*ч/1.4А = 10ч,
т.е. аккумулятор должен заряжаться 10ч
Разрядка: t = Q/Iраз = 14А*ч/0.3А = 47ч,
т.е. лампы горели 47ч. Через лампы прошёл ток 14А*ч, пока аккумулятор не разрядился.
Задача 3
Заряженный аккумулятор имеет ёмкость 28А*ч. 1) Какое количество электричества в кулонах содержит аккумулятор? 2) Какой ток необходим для зарядки аккумулятора за 10ч. Каким током разрядится он за 140ч.?
Решение.
1) 1А*ч = 360 А*с = 3600Кл
28А*ч = 28*3600Кл = 100800 Кл.
2) Iзар = Q/t = 28А*ч/10ч = 2.8А, т.е. аккумулятор зарядится за 10часов током 2.8А
3) Iраз = Q/t = 28А*ч/140ч = 0.2А.
Задача 4
Сколько ампер-часов содержтся в 96480 кулонах (заряд Фарадея)?
1А*ч = 3600А*с = 3600Кл;
96480/3600 = 26.8 А*ч, т.е. 96489 Кл. эквивалентен 26,8 А*ч
Задачи для самостоятельного решения:
1. Какой электрический заряд нужен от гальванического элемента, если он разряжается током 0,05А в течении 12ч.? (0,6 А*ч)
2. Через электродвигатель при токе I проходит количество электричества Q = 7500А*с за время t = 5мин/ Чему равен ток? (30мА)
3. Какой ток протекал по проводнику, если через его поперечное сечение за 30мин прошел заряд 54А*с? (30мА)
4. Через аппарат проходит ток I = 20мА в течение 9мин. Определить количество электричества, которое прошло через аппарат?
5. Аккумулятор ёмкостью 10А*ч заряжается током 4А. Как долго должен заряжаться? (10ч)
Задача 1.
Через медный проводник с площадью поперечного сечения S = 4 мм²
протекает ток I=10А. Какова плотность тока?
Решение:
Плотность тока
J = I/S = 10A/4мм² = 2.5 A/мм²
По площади 1 мм² поперечного сечения протекает ток I = 2.5A;
По всему поперечному сечению S проходит общий ток I = 10А.
По таблице проверить, допустима ли плотность тока 2.5 А/мм²?
Задача 2.
По шине разделительного устройства площадью прямоугольного поперечного сечения (20х80)мм проходит ток I = 1000A. Какова плотность тока в шине?
Решение
Площадь поперечного сечения шины S = 20х80 = 1600 мм². Плотность тока
J = I/S = 1000A/1600 мм² = 0.625A/мм²
Задача 3.
У катушки провод имеет круглое сечение диаметром 0,8мм и допускает плотность тока 2,5А/мм². Какой допустимый ток может проходить по проводу (нагрев не должен превышать допустимый)?
Решение:
Площадь поперечного сечения провода:

 Допустимый ток:
Допустимый ток:
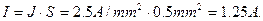
Задача 4.
Допустимая плотность тока для обмотки трансформатора J = 2.5 А/мм²
Через обмотку проходит ток I = 4A. Каким должно быть поперечное сечение круглого проводника, чтобы обмотка не перегревалась?
Решение:
Площадь поперечного сечения
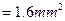
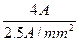
S = I/J =
Этому сечению соответствует диаметр провода 1.42мм.
Задача 5.
По изолированному медному проводу сечением 4 мм² проходит максимально допустимый ток 38А (см таблицу). Какая допустимая плотность тока? Чему равны допустимые плотности токов для медных проводов с площадями поперечного сечения 1, 10, 16 мм²?
Решение.
1) Допустимая плотность тока
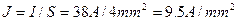
2) Для сечения 1 мм² допустимая плотность тока (см табл)
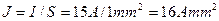
3) Для сечения 10 мм² допустимая плотность тока
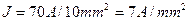
4) Для сечения 16 мм² допустимая плотность тока
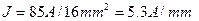
Допустимая плотность тока с увеличением сечения кабеля тоже действительна для проводов с изоляцией класса В.
Задачи для самостоятельного решения.
1. Через обмотку трансформатора должен протекать ток I = 4A. Каким должно быть сечение обмоточного провода при допустимой плотности тока J = 2.5 А/мм² (S = 1.6 мм²)
2. По проводу диаметром 0,3 мм проходит ток 100А. Какова плотность тока (J = 1.415 А/мм²)
3. По обмотке электромагнита из медного изолированного провода диаметром d = 2.26мм (без учёта изоляции) проходит ток 10А. Какова плотность тока? (J= 2.5 А/мм²)
§
Напряженность точечного заряда в вакууме
где ![]() –
–
радиус-вектор, направленный от заряда в данную точку поля, а r – модуль
этого вектора.
Направление этого вектора определяет направление силы, действующей на
положительный заряд, помещенный в рассматриваемую точку поля (рис. 1.3).
Если известна
напряженность поля в какой-либо точке, то тем самым определена и сила,
действующая на электрический заряд, помещенный в эту точку:
Напряженность поля системы точечных
неподвижных зарядов равна векторной сумме напряженностей полей, которые
создавали бы каждый из зарядов в отдельности:
В
качестве примера рассмотрим поле двух точечных зарядов q1 и
q2 (рис. 1.4). ![]() –
–
напряженность поля в точке а, создаваемая зарядом q1, а
![]() –
–
напряженность поля заряда q2.![]() –
–
напряженность результирующего поля.
Если заряженное тело
настолько велико, что его нельзя рассматривать как точечный заряд, то в этом
случае необходимо знать распределение зарядов внутри тела, пространственное
расположение зарядов принято описывать с помощью: объемной плотности заряда
(r),
поверхностной плотности заряда (s)
и линейной плотности заряда (l).
Эти величины определяются формулами:
где dq – заряд,
заключенный соответственно в объеме
dV, на поверхности dS и на длине dl.
При
непрерывном распределении зарядов
Например, если
заряд распределен по объему с плотностью r,
то формула (1.9) примет вид
где
интегрирование проводят по всему пространству, в котором r
отлично от нуля.
Если вектор
напряженности в любой точке поля постоянен по модулю и направлению, то такое
поле называется однородным. Таким полем является, например, электрическое поле
между двумя параллельными металлическими пластинами, заряженными разноименными
зарядами (плоский конденсатор), если расстояние между пластинами мало по
сравнению с размерами пластин (рис. 1.8).
Основной задачей
электростатики является вычисление полей заряженных тел. Найти напряженность
поля заряженного тела можно с помощью:
1)
принципа суперпозиции – это сложная математическая задача, решаемая только в
некоторых простых случаях;
2) теоремы
Гаусса, которая упрощает расчеты, но только в случае бесконечной плоскости,
бесконечной нити (цилиндра) или сфер и шаров (см. ниже).
Сначала введем понятие «поток
вектора» – это скалярная величина.
Поток вектора
![]() сквозь
сквозь
произвольную замкнутую площадку S:
Теорема Гаусса.
Поток Ф вектора ![]() сквозь
сквозь
произвольную замкнутую поверхность S
равен алгебраической сумме зарядов, заключенных внутри этой поверхности,
деленной на e0:
Если заряд
распределен в пространстве с объемной плотностью r,
то теорема Гаусса для электрического поля в вакууме:
Рассмотрим
некоторые простые примеры вычисления электрического поля с помощью теоремы
Гаусса. Чтобы найти напряженность с помощью теоремы Гаусса, нужно взять
интеграл. Надо суметь выбрать такую замкнутую поверхность, в каждой точке
которой было бы Е = const,
иcosa
= const.
Тогда в левой части теоремы Е и cosa можно будет вынести из-под
знака интеграла. Поэтому практически теорему Гаусса можно применить только в
следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная
плоскость.
Напряжённость электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряжённости поля совокупности дискретных источников имеем:
- E→=E→1 E→2 E→3 …,{displaystyle {vec {E}}={vec {E}}_{1} {vec {E}}_{2} {vec {E}}_{3} dots ,}
где каждое
- E→i=14πε0qi(Δr→i)2Δr→i|Δr→i|,{displaystyle {vec {E}}_{i}={frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec {r}}_{i})^{2}}}{frac {Delta {vec {r}}_{i}}{|Delta {vec {r}}_{i}|}},}
- Δr→i=r→−r→i.{displaystyle Delta {vec {r}}_{i}={vec {r}}-{vec {r}}_{i}.}
Подставив, получаем:
- E→(r→)=∑i14πε0qi(Δr→i)2Δr→i|Δr→i|,{displaystyle {vec {E}}({vec {r}})=sum limits _{i}{frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec {r}}_{i})^{2}}}{frac {Delta {vec {r}}_{i}}{|Delta {vec {r}}_{i}|}},}
- Δr→i=r→−r→i.{displaystyle Delta {vec {r}}_{i}={vec {r}}-{vec {r}}_{i}.}
Для непрерывного распределения аналогично:
Общие сведения
Мы живём в океане магнитных и электрических полей. Подобно поведению океана в штиль эти поля могут быть более и менее стабильными, превращаясь в шторм в настоящие бури.
Нам с детства известно свойство магнитной стрелки компаса указывать на север под действием постоянного геомагнитного поля Земли. В своё время изобретение компаса сыграло огромную роль в истории человечества, особенно с развитием мореплавания.
В отличие от магнитного поля, электрическое поле Земли почти ничем не проявляет себя в обыденной жизни, и без специальных приборов мы выявить его, как правило, не можем. Хотя иногда мы наблюдаем проявление электрического поля, расчёсывая вымытые и высушенные волосы пластмассовой расчёской или проводя той же расчёской над кусочками целлофана или бумаги, которые, преодолевая земное притяжение, подпрыгивают со стола, прилипая к расчёске.
Но стоит прийти электрической буре, как мы чувствуем её приближение без всяких приборов. Мы видим сполохи далёких зарниц приближающейся грозы, и слышим далекие раскаты грома. Появляются помехи при приёме радио и телевизионных сигналов; разряды молний могут вывести из строя радио- и электронную аппаратуру, линии связи и электропередач.
Примером может служить авария электроснабжения в Нью-Йорке в 1977 году, когда, после серии попаданий молний в различные ЛЭП, без электроснабжения остался почти весь восьмимиллионный город. Геомагнитные бури космических масштабов также могут привести к авариям электроснабжения городов и стран (Квебекская авария в 1989 году), или вызвать перебои в телеграфной связи на целых континентах (Событие Каррингтона в 1859 году).
По современным представлениям, отдельные изменяющиеся во времени электрические и магнитные поля образуют единые электромагнитные поля, изменяющиеся с меньшей или большей частотой. Их спектр чрезвычайно широк — от инфранизких частот в доли герца до квантов гамма-излучения с частотой в эксагерцы.
Любопытный, но малоизвестный факт: в узком радиодиапазоне спектра, на котором ведётся телевизионное вещание и работают спутники связи, мощность излучаемого Землёй сигнала превосходит мощность излучения Солнца! Некоторые радиоастрономы предлагают вести поиск внеземных цивилизаций, сравнимых с нашей цивилизацией, по этому признаку.
Важнейшей характеристикой электрического (равно как и магнитного) поля является его напряжённость. Превышение этого параметра выше определённого значения для данной среды (для воздуха это 30 кВ/см) приводит к электрическому пробою — искровому разряду.
Мощность отдельной молнии при средних значениях напряжения в 20 млн. вольт и тока в 20 тысяч ампер может составлять 200 млн киловатт (учитывая, что при разряде молнии напряжение падает с максимального значения до нуля). А за одну мощную грозу выделяется столько же энергии, сколько потребляет всё население США за 20 минут.
Учитывая то обстоятельство, что на Земле ежесекундно гремят более 2000 гроз одновременно, освоение энергии атмосферного электричества представляется чрезвычайно заманчивым. Существуют множество проектов по перехвату молний специальными громоотводами или инициализации разряда молнии; в этом плане мы уже имеем технологии, позволяющие вызвать разряд запуском малых ракет или воздушных змеев, связанных проводниками с поверхностью Земли.
Более перспективными представляются разработки на основе ионизации атмосферы лучами мощных лазеров или микроволнового излучения и создании таким образом проводящих каналов для разряда молний, что позволяет устранить необходимость материальных затрат, связанных с испарением проводников после удара молнии.
По сути дела нам не требуется генерации собственно электричества — остаётся только организовать его приём, хранение и преобразование в более удобную для практических целей форму — но пока эта задача возлагается на будущие технологии и устройства. Возможным решением проблем могут стать новые материалы вроде графена, и супермагниты на сверхпроводниках, либо создание ионисторов с невероятно высокой плотностью запасаемой энергии.
А может быть осуществится мечта гения от электричества — американца сербского происхождения Николы Теслы; и мы сумеем преобразовать энергию гроз в единое энергетическое поле, которое позволит получать электроэнергию в требуемом количестве в любом месте Земли и даже в её атмосфере.
Ведь удалось же Тесле во время проведения экспериментов по получению искусственных молний в июне 1889 года в своей лаборатории, расположенной в Колорадо-Спрингс, добиться такой передачи электрической мощности без проводов, что лошади в округе валились с ног, получив электрический удар через металлические подковы!
Но, говорят же, что если опережаете человечество на один шаг — вы точно гений! Но если на два шага — вы безумец!
Примечания
- ↑Напряжённость электрического поля // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если E→{displaystyle {vec {E}}} одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия E→{displaystyle {vec {E}}} в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле E→{displaystyle {vec {E}}} — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
- ↑Хотя исторически многие из них были открыты раньше.
Сила, с которой электромагнитное поле действует на заряженные частицы
Полная сила, с которой электромагнитное поле (включающее, вообще говоря, электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
- F→=qE→ qv→×B→,{displaystyle {vec {F}}=q{vec {E}} q{vec {v}}times {vec {B}},}
где q{displaystyle q} — электрический заряд частицы, v→{displaystyle {vec {v}}} — её скорость,
B→{displaystyle {vec {B}}} — вектор магнитной индукции (основная характеристика магнитного поля); косым крестом ×{displaystyle times } обозначено векторное произведение. Формула приведена в единицах СИ.
Эта формула является более общей по сравнению с формулой, данной в определении напряжённости электрического поля, так как включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
Частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — если воспользоваться обычным для физики приёмом разбиения сложного тела на маленькие (математически — бесконечно малые) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы Лоренца. Разумеется, для того, чтобы эта формула была применена (даже в простых случаях, таких, как расчёт силы взаимодействия двух точечных зарядов), необходимо уметь рассчитывать E→{displaystyle {vec {E}}} и B→{displaystyle {vec {B}}}.
Остальные формулы, применяемые для расчёта электромагнитных сил (например, формулу для силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца или частными случаями её применения.
Уравнения максвелла
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряжённости электрического поля:
- divE→=ρε0,rotE→=−∂B→∂t,divB→=0,rotB→=μ0j→ 1c2∂E→∂t.{displaystyle {begin{aligned}operatorname {div} {vec {E}}&={frac {rho }{varepsilon _{0}}},&operatorname {rot} {vec {E}}&=-{frac {partial {vec {B}}}{partial t}},\operatorname {div} {vec {B}}&=0,&operatorname {rot} {vec {B}}&=mu _{0}{vec {j}} {frac {1}{c^{2}}}{frac {partial {vec {E}}}{partial t}}.end{aligned}}}
Здесь ρ{displaystyle rho } — плотность заряда, j→{displaystyle {vec {j}}} — плотность тока, ε0{displaystyle varepsilon _{0}} — электрическая постоянная, μ0{displaystyle mu _{0}} — магнитная постоянная, c{displaystyle c} — скорость света (уравнения записаны в системе СИ). В приведённом виде уравнения Максвелла являются «уравнениями для вакуума» (их более общий вариант, применимый и для описания поведения электромагнитного поля в среде, а также иные формы записи уравнений — см. в статье Уравнения Максвелла).
Этих четырёх уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (не квантовую) электродинамику, то есть они представляют её полные законы. Для решения реальных задач с их помощью необходимы ещё уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также дополнительная информация о конкретных свойствах рассматриваемых физических тел и сред (их упругости, электропроводности, поляризуемости и др.) и о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
Электростатика
Теоретически и практически важным случаем является ситуация, когда заряженные тела неподвижны (например, исследуется состояние равновесия) или скорость их движения достаточно мала, чтобы можно было приближённо воспользоваться способами расчета, справедливыми для неподвижных тел. Этим случаем занимается раздел электродинамики, называемый электростатикой.
Как указано выше, напряжённость электрического поля в этом случае выражается через скалярный потенциал как
- E→=−∇φ,{displaystyle {vec {E}}=-nabla varphi ,}
или
- Ex=−∂φ∂x,Ey=−∂φ∂y,Ez=−∂φ∂z,{displaystyle E_{x}=-{frac {partial varphi }{partial x}},quad E_{y}=-{frac {partial varphi }{partial y}},quad E_{z}=-{frac {partial varphi }{partial z}},}
то есть электростатическое поле оказывается потенциальным полем.
(φ{displaystyle varphi } в этом случае — случае электростатики — принято называть электростатическим потенциалом).
Правомерно и обратное соотношение:
- φ=−∫E→⋅dl→.{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}.}
Уравнения Максвелла при этом также сильно упрощаются (уравнения с магнитным полем можно вообще исключить, а в уравнение с дивергенцией можно подставить −∇ϕ{displaystyle -nabla phi }) и сводятся к уравнению Пуассона:
- Δφ=−ρε0,{displaystyle Delta varphi =-{frac {rho }{varepsilon _{0}}},}
а в областях, свободных от заряженных частиц, — к уравнению Лапласа:
- Δφ=0.{displaystyle Delta varphi =0.}
Учитывая линейность этих уравнений, а следовательно, применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряжённость поля, создаваемого любым распределением зарядов (суммируя решения для точечных зарядов).








































