ИЗМЕРЕНИЕ РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ

Приложение в(справочное)основные принципы решения уравнения расхода

B.1 Задачи, решаемые с помощью
уравнения расхода

Решение
уравнения расхода выполняют с целью выбора параметров СИ, геометрических
характеристик СУ и ИТ, проверки условий применения расходомера, а также расчета
расхода и количества среды.

Основные
задачи, решаемые с помощью уравнения расхода:

– определение расхода среды по заданным характеристикам ИТ, СУ и
параметрам среды;

– расчет диаметра отверстия СУ по перепаду давления на СУ,
характеристикам среды и ИТ, параметрам потока;

– расчет перепада давления на СУ по заданным характеристикам ИТ,
СУ и параметрам потока;

– расчет внутреннего диаметра ИТ и числа ИТ по заданной
допускаемой скорости среды или по заданным значениям верхней границы диапазона
измерений перепада давления на СУ и относительного диаметра отверстия СУ.

Ниже
приведены основные принципы решения уравнения расхода.

B.2
Определение расхода среды

Коэффициент
истечения СУ (кроме сопел Вентури) и поправочный коэффициент, учитывающий
шероховатость внутренней поверхности ИТ, зависят от числа Reи, следовательно, от значения
расхода среды, поэтому уравнение расхода является неявным уравнением.

Уравнение
расхода (см. 5.1.4) может быть решено методом итераций.

Итерационный
процесс рекомендуется проводить по числу Re (см. ниже) или по расходу среды [см. ГОСТ
8.586.5
(раздел 8)].

Для
этого уравнение расхода (см. 5.1.4) записывают в общем неявном виде относительно
числа Re:

                                                                  (B.1) где
– коэффициент истечения, рассчитанный для значения числа Re, равного 10⁶;– поправочный коэффициент, учитывающий шероховатость внутренней
поверхности ИТ, рассчитанный при числе Re= 10⁶;

Re* – модифицированное число
Рейнольдса, которое рассчитывают по формуле

)                                     (B.2)

Уравнение
расхода (см. 5.1.4) с учетом формулы (В.1) может быть решено в следующей
последовательности:

а) рассчитывают С’
и К’ши, применяя
формулу (В.2), вычисляют значение Re*;

б) рассчитывают коэффициент истечения С, поправочный коэффициент Кшпри числе Re = Re* и
вычисляют первое приближение для числа Reпо формуле

                                                                  (B.3)

в) рассчитывают относительную разность δ1,
значений Re1, и Re* по формуле

и
проверяют выполнение неравенства:

                                                                              (B.4)

Если
неравенство (В.4) выполняется, то значение Re1 принимают как решение уравнения (В.1), в другом случае определяют
новое приближение для числа Reпо формуле

                                                                (B.5)

где
С и Кшрассчитывают
при числе Re = Re1.

г) рассчитывают относительную разность δ2значений Re2 и Re1 по формуле

и
проверяют выполнение неравенства:

                                                                              (B.6)

Если
неравенство (В.6) выполняется, то значение Re2 принимают как решение уравнения (В.1), в другом случае
рассчитывают новое приближение для числа Reпо общей формуле

                                                         (B.7)

где
С и Кшрассчитывают
при числе Re, рассчитанном на n-м цикле вычислений,

или

                                               (B.8)

Поиск
новых приближений для числа Reпрекращают
при выполнении неравенства:

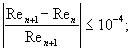                                                              (B.9)

д)
используя вычисленное значение числа Re,
рассчитывают коэффициенты С и Кши значение расхода среды по формуле (5.2).

В.3 Расчет диаметра отверстия СУ

Расчет
диаметра отверстия СУ может быть выполнен по следующим исходным данным:

– qmmin,qmmax∆pв , p, T, ρ, μ, для газа
дополнительно – к;

– D, Rш, для диафрагм – начальное значение радиуса входной кромки
диафрагмы и межконтрольный интервал диафрагмы [см. ГОСТ
8.586.

Расчет
выполняют в следующей последовательности:

а) для газов проверяют выполнение неравенства:

∆pв = 0,25p.                                                                           (B.10)

Если
неравенство (В.10) не выполняется, то расчет прекращают, так как измерение
расхода среды при таком режиме невозможно, или выбирают другой верхний предел
измерений перепада давления, удовлетворяющий неравенству (В. 10);

б) по данным соответствующей части комплекса стандартов [см. ГОСТ
8.586.2 (пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1,
5.3.4.1),  ГОСТ 8.586.

4 (пункты 5.5.2, 5.5.3, 5.5.4)] определяют значения верхней границы ReBи нижней
границы Reв диапазона
допускаемых значений Reдля
выбранного типа СУ;

в) рассчитывают значения верхней границы Remaxи нижней границы Reminрабочего
диапазона значений Reпо формулам:

и
проверяют выполнение неравенств:

Reв ≥ Remax;                                                                           (B.11)

Reн ≤ Remin.                                                                            (B.12)

Если
неравенства (В.11) и (В.12) не выполняются, то расчет прекращают или выбирают
другой тип СУ, для которого неравенства (В.11) и (В.12) выполняются;

г) рассчитывают значение вспомогательной величины А по формуле

                                                                 (B.13)

д)
используя соответствующую часть комплекса стандартов [см. ГОСТ
8.586.2 (пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1, 5.3.4.1)

,
 ГОСТ 8.586.4 (пункты 5.1.2, 5.1.3, 5.1.4)], определяют значения верхней границы
βв и нижней границы βн диапазона допускаемых
значений β для выбранного типа СУ;

е) рассчитывают значения вспомогательных величин В1и В2по формулам:

B1 = E1C1Kш1Kп1 β2в
ε1;

В2 = E2C2Kш2Kп2 β2нε2,                                                       (B.15)

где
Е1, Е2-
коэффициенты скорости входа при βв и βн,
соответственно;

С1,
– коэффициент истечения при Remaxи βв;

С2
– коэффициент истечения при Remaxи βн;

Кп1- поправочный коэффициент Кпдля диафрагм при βв
(для остальных СУ Кп1=
1);

Кп2- поправочный коэффициент Кпдля диафрагм при рн
(для остальных СУ Кп2=
1);

Кш1- поправочный коэффициент Кшпри Remaxи βв
(для труб Вентури Кш1=
1);

Кш2- поправочный коэффициент Кшпри Remaxи βн
(для труб Вентури Кш2=
1);

ε1
– коэффициент расширения при βв, ∆рв, к и р;

ε2
– коэффициент расширения при βн> ∆рв> к
и р.

Рассчитывают
значения вспомогательных величин δ1 и δ2 по
формулам:

δ1 = (B1
– A)/A;

δ2 = (B2
– A)/A;

Если
величины δ1 и δ2 имеют одинаковый знак, то
расчет прекращают, так как в диапазоне допускаемых значений δ не
существует значения, удовлетворяющего исходным данным.

Если
величины δ1 и δ2 имеют разные знаки, то расчет
продолжают;

ж)
относительно неизвестной величины δ решают следующее уравнение:

A = ECKшKпβ2ε.                                                                    (B.16)

Решение
уравнения (В.16) может быть выполнено любым итерационным методом. При
применении метода бисекции решение уравнения выполняют в следующей последовательности:

– рассчитывают значение р по формуле

Β = (βв βн)/2;                                                                       (B.17)

– для значения β рассчитывают значение вспомогательной
величины В по формуле

В = Е С Кш  Кп, β2 ε,                                                             (B.18)

где
расчет С и Кшвыполняют при Remax, а значение
е вычисляют при ∆рв,
к и р;

– проверяют выполнение неравенства:

                                                       (B.19)

Если
неравенство (В. 19) не выполняется, то рассчитывают новое значение β по
формуле (В. 17), в которой, если выполняется неравенство В < А принимают βн
= β, рассчитанное на первом шаге итерации, в другом случае принимают
βв = β.

Для
нового значения β по формуле (В.18) рассчитывают значение В и проверяют
неравенство (В.19). Если неравенство не выполняется, то продолжают выбор новых
значений β, используя для замены βв и βн в
формуле (В.17) значение β, рассчитанное на предыдущем шаге итерации.

Выбор
значений β осуществляют до выполнения неравенства (В.19);

и)
для найденного значения β, используя соответствующую часть комплекса
стандартов [см.
ГОСТ
8.586.2 (пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1, 5.3.4.1)

,  ГОСТ 8.586.4 (пункты
5.5.2, 5.5.3, 5.5.4)], определяют верхнее (Reв) и нижнее (Reн) значения допускаемого диапазона значений чисел Reи проверяют неравенства (В.11) и
(В.12).

Если неравенства выполняются, то значение р, рассчитанное в
соответствии с перечислением ж), принимают как окончательное, в другом случае
расчет диаметра отверстия СУ при заданных исходных данных невозможен;

к)
используя значение β, найденное по перечислению ж), вычисляют диаметр
отверстия СУ по формуле

d20 = β D/Kсу.

Примечание – При расчете внутреннего
диаметра отверстия диафрагмы дополнительно проверяют, что d20находится в диапазоне допустимых значений [см. ГОСТ
8.586.

2 (пункт 5.3.1)]. Если данное условие выполняется, то значение d20считается найденным.

В.4 Расчет диапазона изменений перепада давления на СУ

Расчет
диапазона изменений перепада давления на СУ может быть выполнен по следующим
исходным данным:

–
qmmin, qmmax, p, ρ, μ, для газов дополнительно – к

– β, d, D,
Rш, для диафрагм – начальное значение радиуса входной кромки диафрагмы
и межконтрольный интервал [см. ГОСТ
8.586.

Расчет
выполняют в следующей последовательности:

а)
рассчитывают значения верхней границы Remaxи нижней
границы Reminрабочего
диапазона значений Reпо формулам:

и
проверяют выполнение неравенств:

Reв ≥ Remax;                                                                            (B.21)

Reн ≤ Remin.                                                                            (B.22)

где
Reв и Reн –
наибольшее и наименьшее допускаемые значения числа Re, для выбранного типа СУ и значения β [см.

ГОСТ
8.586.2 (пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1,
5.3.4.1),  ГОСТ 8.586.

Если
неравенства (В.21) и (В.22) не выполняются, то расчет прекращают или выбирают
другой тип СУ, для которого выполняются данные неравенства;

б) рассчитывают значение вспомогательной величины Sпо формуле

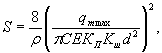                                                      (B.23)

в) если среда – жидкость, то принимают верхнюю границу диапазона
изменений перепада давления на СУ равной значению S. Если среда –
газ, то относительно неизвестной величины ∆р решают следующее уравнение:

∆p
= S ε-2.                                                                               (B.24)

Решение
уравнения (В.24) может быть выполнено итерационным методом:

– рассчитывают значение ∆р1 по формуле

∆p1 = S/0,9409;

– проводят вычисления на первом шаге итерации

∆p2 = S ε2-2,

где
ε1 – коэффициент расширения при ∆р = ∆p1.

– проводят вычисления на втором шаге итерации

∆p3
= S ε2-2,

где
ε2 – коэффициент расширения при ∆р = ∆р2.

– рассчитывают верхнюю границу диапазона изменений перепада
давления на СУ по формуле

                                          (B.25)

г) рассчитывают вспомогательную величину S1по формуле

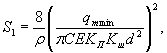                                                (B.26)

где
С и Кшрассчитывают
при Remin;

д) если среда – жидкость, то нижнюю границу диапазона изменений
перепада давления на СУ принимают равной значению S1Если среда – газ, то относительно неизвестной величины ∆р решают следующее уравнение:

∆p = S1ε-2.                                                                              (B.27)

Решение
уравнения (В.27) может быть выполнено методом, изложенным выше [см.
перечисление в)]. За нижнюю границу диапазона изменений перепада давления на СУ
принимают результат расчета.

В.5 Расчет внутреннего диаметра ИТ и числа ИТ

В.5.1 Расчет внутреннего диаметра и числа ИТ по заданной
допускаемой скорости среды

8.5.1.1 Исходными данными для расчета являются тип СУ и следующие
параметры потока и среды: , q_mmin, ρ и
μ.

Расчет
выполняют в следующей последовательности. Вспомогательные параметры Аmin, Аmax, С рассчитывают по формулам:

                                                                      (B.28)                                                                     (B.29)                                                                          (B.30)

Значения
верхних и нижних границ диапазона допускаемых значений Re, β, Dи dдля выбранного типа СУ определяют в соответствии
с ГОСТ
8.586.

2
(пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1,
5.3.4.1), ГОСТ
8.586.4 (пункты 5.1.2, 5.1.3, 5.1.4,
5.5.2,5.5.3, 5.5.4).

Для
диафрагм принимают Reн = 5000, для
сопел ИСА 1932 принимают два значения Reн1 =70000 и Reн2 = 20000.

B.5.1.2 Для диафрагм с фланцевым
способом отбора давления проверяют условие

                                                       (B.31)

Если
неравенство (В.31) не выполняется – расчет невозможен, необходимо изменить
исходные данные.

B.5.1.3 Параметры Nн, Nв, N*нрассчитывают по формулам:

Nн = С/D2в;                                                                            (B.32)

Nв = С/ D2в                                                                                                     (B.33)

N*н = (1/С) (Amax/Reв)2.

Для
всех СУ, кроме сопел ИСА 1932, дополнительно рассчитывают параметр N*н по формуле

N*в = (1/С) (Amin/Reн)2.

Для
сопел ИСА 1932 дополнительно рассчитывают параметры N*в1,, N*в2
по формулам:

N*в1 = (1/С) (Amin/Reн1)2.

N*в2 = (1/С) (Amax/Reн2)2.

Значения
параметров, рассчитанных по формулам (В.32) – (В.37), с индексом «н» округляют
до ближайшего большего целого, а с индексом «в» округляют до ближайшего
меньшего целого числа.

B.5.1.4 Начальное приближение Nдля числа ИТ
и значения их внутреннего диаметра Dрассчитывают
по формулам:

N = Nmin = max (Nв, N*н);                                                      (B.38)

                                                                          (B.39)

B.5.1.5 Для сопел ИСА 1932
допускаемые границы для β определяются условиями:

N ≤ Nmax1 = min (Nв, N*в1);                                                    (B.40)

N < Nmax2 = min (Nв, N*в2);                                                    (В.41)

0,3
≤ β < 0,44 – при выполнении условия (В.40);

0,3
≤ β < 0,80 – при одновременном выполнении условий (В.40) и
(В.41).

При
нарушении двух условий решение невозможно, необходимо изменить исходные данные.

B.5.1.6 Для труб и сопел Вентури,
эллипсных сопел и диафрагм проверяют условие:

N ≤ Nmax = min (Nв, N*в);                                                      (B.42)

Если
условие (В.42) не выполняется – расчет невозможен, необходимо изменить исходные
данные.

При
выполнении условия (В.42) для труб Вентури и эллипсных сопел расчет закончен,
для сопел Вентури и диафрагм дополнительно проверяют выполнение условия:

max (βнD, dн) ≤ βвD.

Если
условие (В.43) выполняется, то расчет закончен.

Если
условие (В.43) не выполняется, то увеличивают N, рассчитывают новое значение Dпо формуле
(В.39) и повторяют процесс, начиная с проверки условия (В.42).

В.5.2 Расчет внутреннего диаметра и числа ИТ по заданным значениям
верхней границы диапазона измерений перепада давления на СУ и относительного
диаметра отверстия СУ

B.5.2.1 Исходными данными для расчета
являются – тип СУ, β, р,
∆р, qmmax, qmmin, ρ, μ, для газов
дополнительно – к.

Расчет
выполняют в следующей последовательности.

Значения
верхних и нижних границ диапазона допускаемых значений Re, Dи г/для выбранного типа СУ определяют в соответствии с ГОСТ
8.586.

2 (пункт 5.3.1), ГОСТ
8.586.3 (подпункты 5.1.6.1, 5.2.6.1, 5.3.4.1),  ГОСТ 8.586.4 (пункты 5.1.2, 5.1.3,
5.1.4, 5.5.2,5.5.3, 5.5.4).

Для
диафрагм с фланцевым способом отбора давления принимают Reн = 5000.

Вспомогательный
параметр Aрассчитывают по формуле

                                                        (B.44)

B.5.2.2 По формулам (В.28), (В.29)
определяют вспомогательные параметры: Aminи Аmax.

B.5.2.3 Значения верхней границы D*ви нижней границы D*ндиапазона
допускаемых значений внутреннего диаметра ИТ рассчитывают по формулам:

D*н = max(Dн;dн/β);

D*в = Dв.                                                                               (B.46)

B.5.2.4 Параметры рассчитывают по формулам:

Nн = Amax/(ReвD*н);

для всех типов СУ, кроме диафрагм с фланцевым
способом отбора давления

Nв = Amin/(ReнD*в);

для диафрагм с фланцевым способом отбора давления

Nв = min (Nв1;Nв2)

где Nв1 = Amin/(ReнD*в);
Nв2= (Amin/170000)/(β D*в)2.

Значения Nни Nвокругляют в соответствии с В.5.1.3.

При Nв < Nнрешение невозможно, необходимо изменить
исходные данные.

B.5.2.5 При Nн ≤ Nв принимают
число ИТ, удовлетворяющее условию:

Nн ≤ N≤ Nв.                                                                          (B.50)

B.5.2.6 При условии D*н ≤ D≤ D*в относительно Dрешают уравнение

F = (q*mmax
– qmmax)/qmmax = 0.                                                (B.51)

где

q*mmax
= A N C Kш Kп D2.                                                     (B.52)

Значения С, Кш,
Кпв зависимости от выбранного типа СУ определяют в
соответствии с ГОСТ
8.586.2 (пункт 5.3.2,), ГОСТ
8.586.

3 (подпункты 5.1.6.2, 5.1.6.4, 5.2.6.2, 5.3.4.2),  ГОСТ 8.586.4 (пункты 5.5.2, 5.5.3, 5.5.4).

Число Reпри этом
рассчитывают по формуле

Re = Amax/(DN).                                                                     (B.53)

B.5.2.7 Для решения уравнения (В.51) рекомендуется следующий алгоритм:

а) принимают D1 = D*н; D2 = D*в, рассчитывают соответствующие значения qmmax1, qmmax2 – по формуле (В.52) и F1, F2- по
формуле (В.51);

б) принимают

D*=(Dl D2)/2

и рассчитывают соответствующие значения q*mmax- по формуле (В.52), F* – по
формуле (В.51);

при |F*| < 0,001
полученное значение D* принимают в качестве окончательного,
иначе процесс продолжают с перечисления в);

в) при условии F* F1 > 0, принимают D1 = D* и F1= F*;

при условии F* F1 < 0, принимают D2 = D* и F2 = F*

переходят к выполнению перечисления б).

Приложение г(справочное)температурный коэффициент линейного расширения материала

Значения
температурного коэффициента линейного расширения материала СУ и ИТ могут быть
рассчитаны в зависимости от температуры по формуле, полученной на основе данных
[13] и [14]:

αt = 10-6[a0 a1
(t/1000) a2(t/1000)2],                                   (.1)

где a0, a1a2- постоянные коэффициенты,
определяемые в соответствии с таблицей Г.1.

Таблица Г.1 – Значения постоянных коэффициентов a0, a1a2и границы области применения формулы (Г.1)

Окончание таблицы Г.1

Дополнительная информация о значениях
температурного коэффициента линейного расширения для марок стали, не
приведенных в таблице Г.1, приведена в [13].