Измерение скорости потока и расхода жидкости
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рисунок 3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
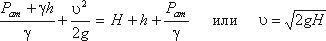
где Н – столб жидкости в трубке Пито.
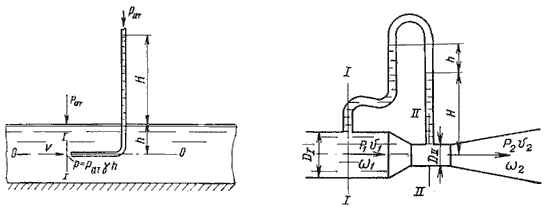
Рисунок 3.7 – Трубка Пито и pасходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рисунок 3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:
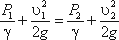
или
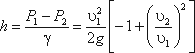
Используя уравнение неразрывности:
Q = υ1ω1 = υ2ω2
сделаем замену в получено выражении:
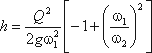
Решая относительно Q, получим
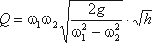
Выражение, стоящее перед 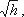 , является постоянной величиной, носящей название постоянной водомера Вентури.
, является постоянной величиной, носящей название постоянной водомера Вентури.
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
§
При наблюдении за движением жидкости в трубах и каналах, можно заметить, что в одном случае жидкость сохраняет определенный строй своих частиц, а в других – перемещаются бессистемно. Однако исчерпывающие опыты по этому вопросу были проведены Рейнольдсом в 1883 г. На рисунке 4.1 изображена установка, аналогичная той, на которой Рейнольдс производил свои опыты.
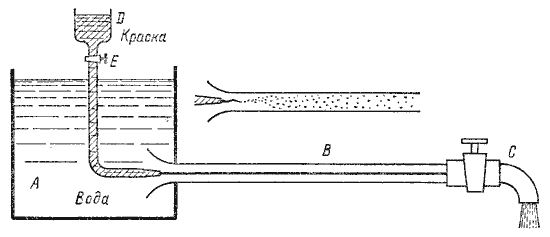
Рисунок 4.1 – Схема установки Рейнольдса
Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.
Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.
Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рисунок 4.1, вверху).
Если уменьшить скорость потока, то восстановится ламинарное течение.
Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ кр.
Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.
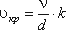
где ν – кинематическая вязкость;
k – безразмерный коэффициент;
d – внутренний диаметр трубы.
Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Reкр и определяется следующим образом:
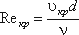 (4.1)
(4.1)
Как показывает опыт, для труб круглого сечения Reкр примерно равно 2300.
Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Reкр течение является ламинарным, а при Re > Reкр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.
Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.
Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рисунок 4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.
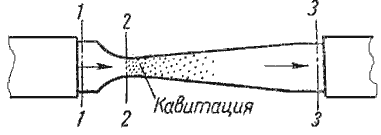
Рисунок 4.2 – Схема трубки для демонстрации кавитации
При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.
Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.
При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.
Таким образом, кавитация – это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.
Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.
§
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью – квадратичную параболу (рисунок 4.3).
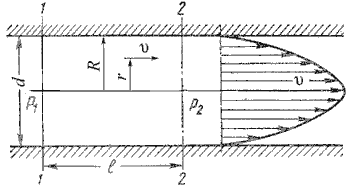
Рисунок 4.3 – Схема для рассмотрения ламинарного потока
Уравнение, связывающее переменные υ и r, имеет следующий вид:
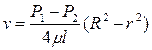 , (4.2)
, (4.2)
где P1 и P2 – давления соответственно в сечениях 1 и 2.
У стенок трубы величина r = R, , значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
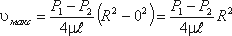
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида:
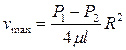 (4.3)
(4.3)
Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равен
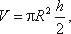
а в нашем случае
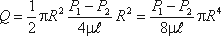 (4.4)
(4.4)
Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид
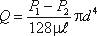
Расход в трубе можно выразить через среднюю скорость:
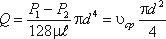
откуда
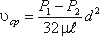 (4.5)
(4.5)
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рисунок 4.3).
Потеря давления в трубопроводе будет равна
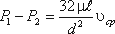 (4.6)
(4.6)
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
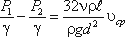
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
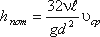 (4.7)
(4.7)
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
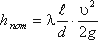 (4.8)
(4.8)
где λ – коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
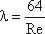 (4.9)
(4.9)
§
Как было указано в п.4.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рисунок 4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ оср, которое данном случае остается постоянным.
Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рисунок 4.5).
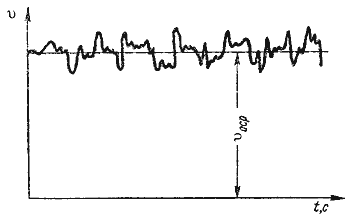
Рисунок 4.4 – Пульсация скорости в турбулентном потоке

Рисунок 4.5 – Характер линий тока в турбулентном потоке
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рисунок 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.
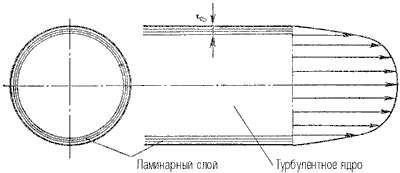
Рисунок 4.6 – Модель турбулентного режима движения жидкости
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
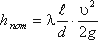
Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора – относительной шероховатости Δ/d (или Δ/r0, где r0 – радиус трубы).
Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r 0. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рисунок 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r0.
Прямая I соответствует ламинарному режиму движения жидкости. Далее на графике можно рассматривать три области. Первая область – область малых Re и Δ/r0, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рисунок 4.7 прямой II ). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d / Δ э) коэффициент λ определяется по полуэмпирической формуле Блазиуса
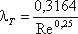 (4.10)
(4.10)
Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб
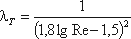 (4.11)
(4.11)
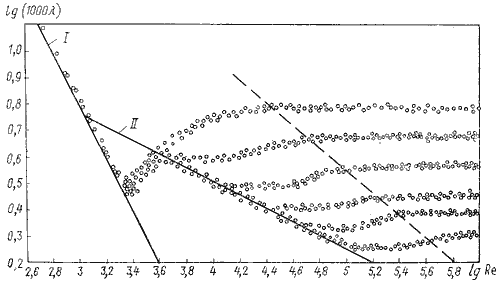
Рисунок 4.7 – График Никурадзе
Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров – числа Re и относительной шероховатости Δ/r0, которую можно заменить на Δэ. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:
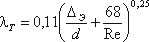 (4.12)
(4.12)
где Δэ – эквивалентная абсолютная шероховатость.
Характерные значения Δэ (в мм) для труб из различных материалов приведены ниже:
| Стекло | |
| Трубы, тянутые из латуни, свинца, меди | 0…0,002 |
| Высококачественные бесшовные стальные трубы | 0,06…0,2 |
| Стальные трубы | 0,1…0,5 |
| Чугунные асфальтированные трубы | 0,1…0,2 |
| Чугунные трубы | 0,2…1,0 |
Третья область – область больших Re и Δ/r0, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
Определение λ для этой области производят по упрощенной формуле Альтшуля:
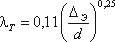
или по формуле Прандтля – Никурадзе:
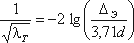
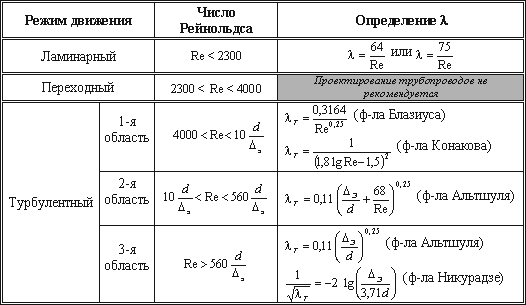
Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δэ. Для удобства сводные данные по определению λ представлены в таблице 4.1.
Пользоваться приведенными в таблице 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рисунок 4.8), при помощи которой по известным Re и Δэ/ d весьма просто определяется λ.
Таблица 4.1 – Таблица для определения коэффициента гидравлического трения
§
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
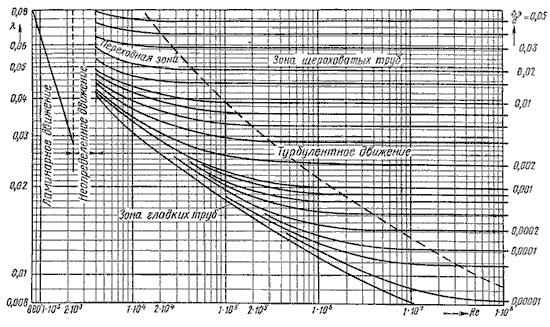
Рисунок 4.8 – Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
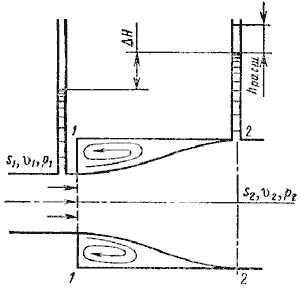
Рисунок 4.9 – Внезапное расширение трубы
При внезапном расширении русла (трубы) (рисунок 4.9) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 – в плоскости расширения трубы и 2-2 – в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:
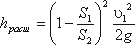 (4.13)
(4.13)
где S1, S2 – площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
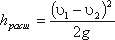
Выражение ( 1 – S1/S2 )2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом
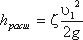 (4.14)
(4.14)
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рисунок 4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
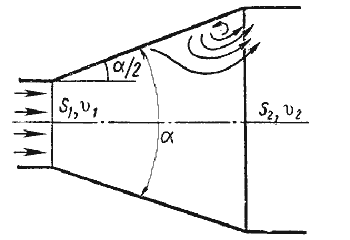
Рисунок 4.10 – Постепенное расширение трубы
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
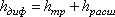
где hтр и hрасш – потери напора на трение и расширение (вихреобразование).
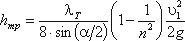 (4.15)
(4.15)
где n = S2/S1 = ( r2/r1 ) 2 – степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении русла:
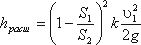 (4.16)
(4.16)
где k – коэффициент смягчения, при α= 5…20°, k = sinα.
Учитывая это полную потерю напора можно переписать в виде:
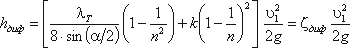
откуда коэффициент сопротивления диффузора можно выразить формулой
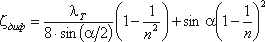
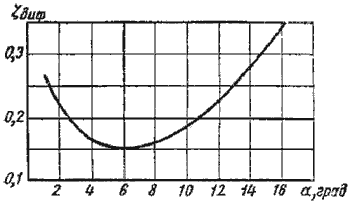
Рисунок 4.11 – Зависимость ζдиф от угла
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
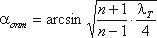
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рисунок 4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рисунок 4.12).
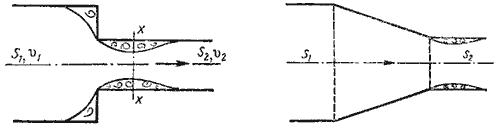
| Рисунок 4.12 – Внезапное сужение трубы | Рисунок 4.13 – Конфузор |
Полная потеря напора определится по формуле:
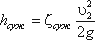
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:
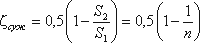 (4.17)
(4.17)
в которой n = S1/S2 – степень сужения.
При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζсуж = 0,5.
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рисунок 4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
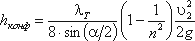 (4.17)
(4.17)
где коэффициент сопротивления конфузора определяется по формуле:
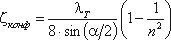 (4.18)
(4.18)
в которой n = S1/S2 – степень сужения.
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рисунок 4.14).
Рисунок 4.14 – Сопло
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рисунок 4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
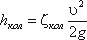
где ζкол – коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рисунок 4.16).
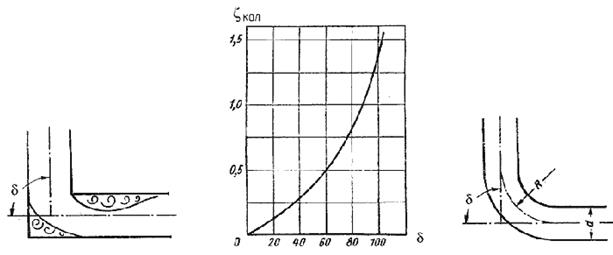
| Рисунок 4.15 – Внезапный поворот трубы | Рисунок – 4.16. Зависимости ζкол от угла δ | Рисунок 4.17 – Отвод |
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рисунок 4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
Для отводов круглого сечения с углом δ= 90 и R/d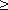 1 при турбулентном течении можно воспользоваться эмпирической формулой:
1 при турбулентном течении можно воспользоваться эмпирической формулой:
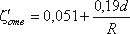
Для углов δ 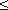 70° коэффициент сопротивления
70° коэффициент сопротивления
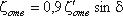
а при δ 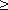 100°
100°
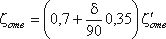
Потеря напора в колене определится как
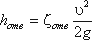
Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.
§
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рисунок 5.1).
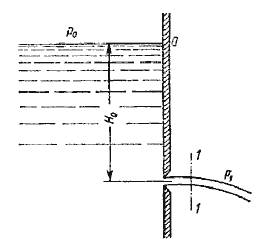
Рисунок 5.1 – Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.
Степень сжатия оценивается коэффициентом сжатия:
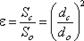 (5.1)
(5.1)
где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.
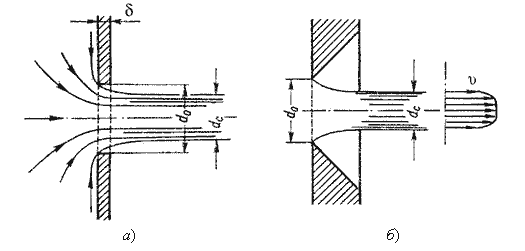
Рисунок 5.2 – Истечение через круглое отверстие
Скорость истечения жидкости через отверстие такое отверстие:
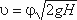 (5.2)
(5.2)
где Н – напор жидкости, определяется по формуле:
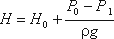 (5.3)
(5.3)
φ- коэффициент скорости:
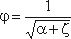
где α – коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
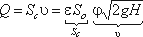
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
В итоге получаем расход
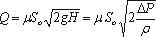 (5.4)
(5.4)
где ΔР – расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача – определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рисунок 5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости:
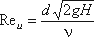 (5.5)
(5.5)
где ν – кинематическая вязкость.
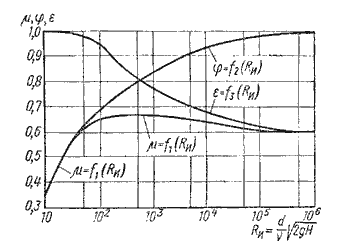
Рисунок 5.3 – Зависимость ε, φ и от числа
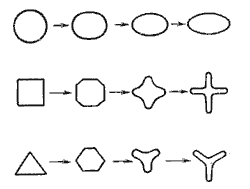
Рисунок 5.4 – Инверсия струй
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рисунок 5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
§
Внешней цилиндрической насадкой называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рисунок 5.7).
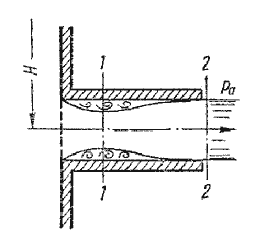
Рисунок 5.7 – Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:
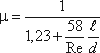 (5.8)
(5.8)
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадкой 2-2 и преобразовать его, то можно получить падение давления внутри насадка
P2 – P1 0,75Hgρ
0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
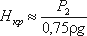
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н  Нкр происходит изменение режима истечения, переход от первого режима ко второму (рисунок 5.8).
Нкр происходит изменение режима истечения, переход от первого режима ко второму (рисунок 5.8).
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
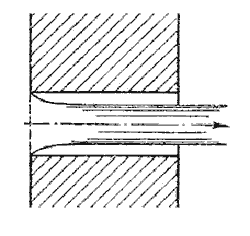
Рисунок 5.8 – Второй режим истечения через насадок
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рисунке 5.9 даны различные типы насадов и указаны значения соответствующих коэффициентов.

Рисунок 5.9 – Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся конические; в – коноидальные; г – внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
§
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рисунок 5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
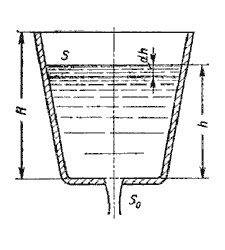
Рисунок 5.10 – Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:
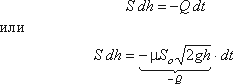
где dh – изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
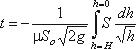
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения
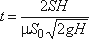 (5.9)
(5.9)
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рисунок 5.12) выразим зависимость переменной площади S от h:
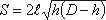
где l – длина цистерны; D – диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным:

§
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рисунок 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рисунок 5.14).
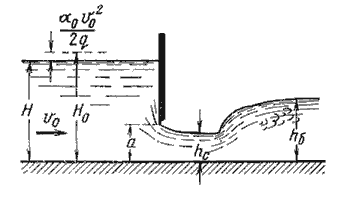
Рисунок 5.13 – Истечение из-под затвора через незатопленное отверстие
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:
hc = ε’a (5.10)
где ε’ – коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε’ = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:
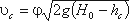
где φ – коэффициент скорости,
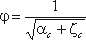
где Н0 – напор с учетом скорости подхода,
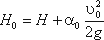
Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:
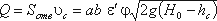 (5.11)
(5.11)
где S – площадь отверстия, S = ab.
При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:
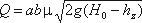
где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под затвора струи.
Глубина hzопределяется из зависимости
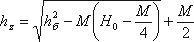
в которой
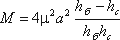
а hб – глубина в отводящем канале (бытовая глубина).
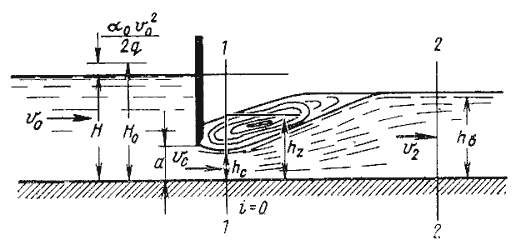
Рисунок 5.14 – Истечение из-под затвора при затопленном отверстии
§
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид
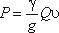 (5.12)
(5.12)
На рисунок 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рисунок 5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
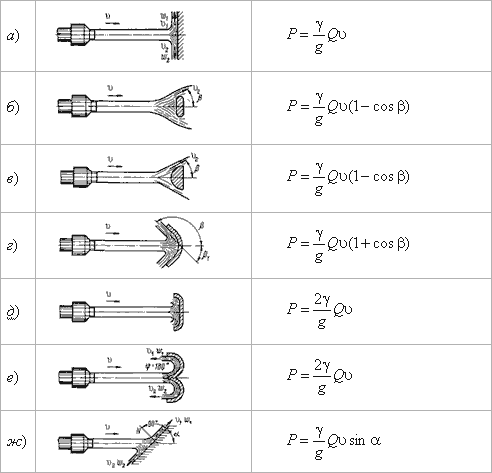
Рисунок 5.15 – Взаимодействие струи жидкости с неподвижной поверхностью
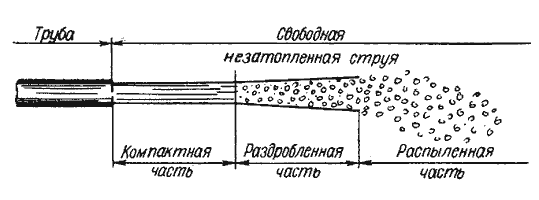
Рисунок 5.16 – Составные части свободной струи
§
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рисунок 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z1 и избыточное давление Р1, а в конечном сечении 2-2 – соответственно z2 и Р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.
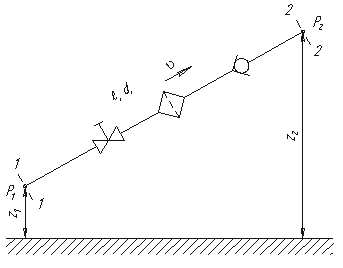
Рисунок 6.1 – Схема простого трубопровода
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α1 = α2, то скоростной напор можно не учитывать. При этом получим
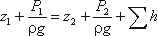
или
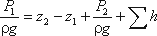
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту:
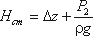
а последнее слагаемое Σh – как степенную функцию расхода
Σh =KQm
тогда
Hпотр = Hст KQm
где K – величина, называемая сопротивлением трубопровода;
Q – расход жидкости;
m – показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно:
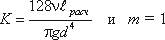
где lрасч = l lэкв.
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
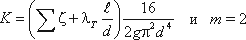
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном – параболой с показателем степени равном двум (рисунок 6.2, б).
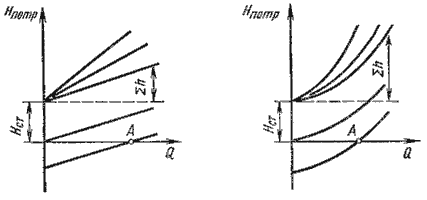
Рисунок 6.2 – Зависимости потребных напоров от расхода жидкости в трубопроводе
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода. Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Σh= f(q)
§
Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным или параллельным.
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рисунок 6.3, а).
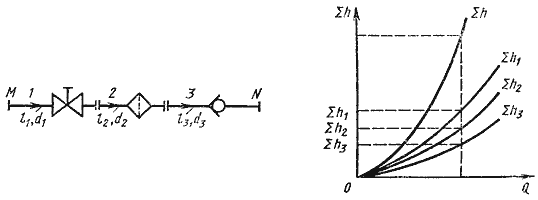
Рисунок 6.3 – Последовательное соединение трубопроводов
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Q1 = Q2 = Q3 = Q
ΣhM-N= Σh1 Σh2 Σh3 (6.1)
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рисунок 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
Параллельное соединение. Такое соединение показано на рисунок 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.
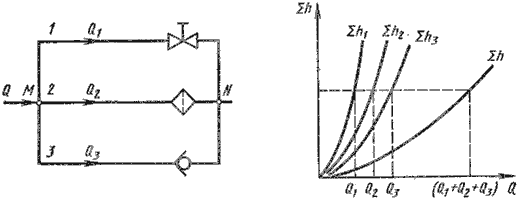
Рисунок 6.4 – Параллельное соединение трубопроводов
Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали (т.е. до разветвления и после слияния) – через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали:
Q = Q1 Q2 Q3
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Σh1 = HM – HN; Σh2 = HM – HN; Σh3 = HM – HN
Отсюда делаем вывод, что
Σh1= Σh2= Σh3
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
Σh1 = K1Q1m; Σh2 = K2Q2m; Σh3 = K3Q3m
где K и m – определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рисунок 6.3, б.
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение – место разветвления (или смыкания) труб.
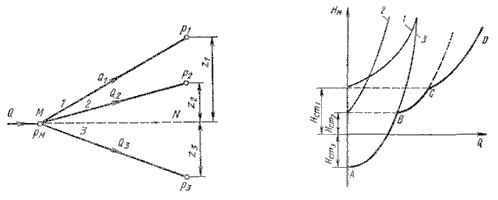
Рисунок 6.5 – Разветвленный трубопровод
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рисунок 6.5, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:
Q = Q1 Q2 Q3
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)
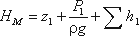
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем
HM = Hст 1 KQ1m
Аналогично для двух других трубопроводов можно записать
HM = Hст 2 KQ2m
HM = Hст 3 KQ3m
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рисунок 6.5, б) – сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM > Hст1.
§
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рисунок6.6, а) или с разветвлениями (рисунок 6.6, б).
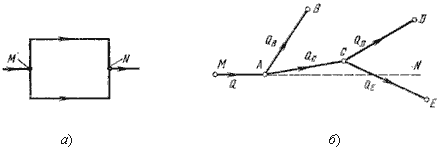
Рисунок 6.6 – Схемы сложных трубопроводов
Рассмотрим разомкнутый сложный трубопровод (рисунок 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M – N и избыточные давления в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
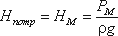
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:
уравнение расходов:
Q = QB = QD = QE
уравнение равенства потребных напоров для ветвей CD и CE
Hст D KCDQDт = Hст E KCEQEт
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
Hст B KABQBт = Hст D KCDQDт KAC(QD QE)т
выражение для потребного напора в точке М
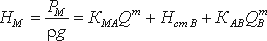
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рисунок 6.7).
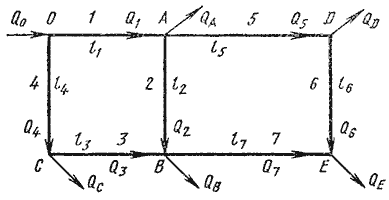
Рисунок 6.7 – Схема сложного кольцевого трубопровода
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие – баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие – баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
§
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рисунок 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рисунок 6.8, б).
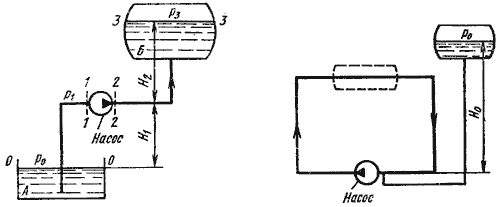
Рисунок 6.8 – Трубопроводы с насосной подачей
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3 (рисунок 6.8, а). Высота расположения оси насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
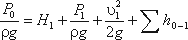
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2 и 3-3:
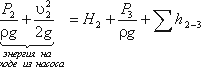
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:
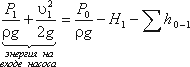
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
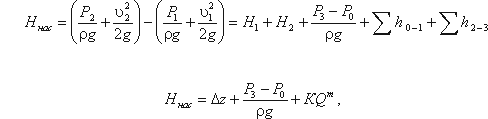
где Δz – полная геометрическая высота подъема жидкости, Δz = H 1 H2;
КQm – сумма гидравлических потерь,
P3и Р0 – давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 – Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
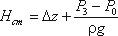
и формулу можно переписать так:
Hнас = Hст KQm
Из этой формулы делаем вывод, что
Hнас = Hпотр
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q) и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рисунок 6.9).
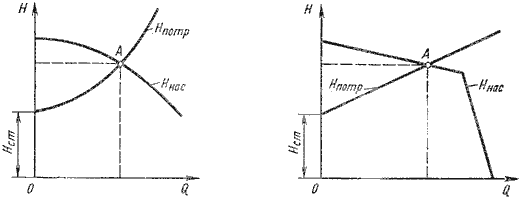
Рисунок 6.9 – Графическое нахождение рабочей точки
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рисунок 6.9 дано два варианта графика: а – для турбулентного режима; б – для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.
§
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рисунок 6.10, а).

Рисунок 6.10 – Стадии гидравлического удара
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n – n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы – растянутыми. Ударное повышение давления распространится на всю длину трубы (рисунок 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рисунок 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 – ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рисунок 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рисунок 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рисунок 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рисунок 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рисунок 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Если давление P0 невелико (P0 < ΔP уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как показано на рис. 6.11, б.
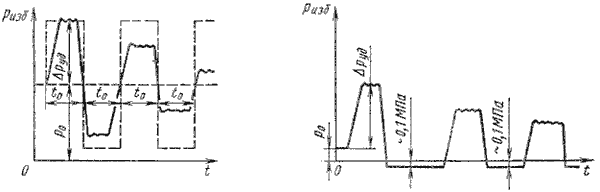
Рисунок 6.11 – Изменение давления по времени у крана
Повышение давления при гидравлическом ударе можно определить по формуле:
ΔPуд = ρυ0c
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
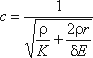 (6.3)
(6.3)
где r – радиус трубопровода;
E – модуль упругости материала трубы;
δ – толщина стенки трубопровода;
K – объемный модуль упругости (см. п.1.3) .
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E =  , то скорость ударной волны определится из выражения
, то скорость ударной волны определится из выражения
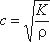
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 – 1400 м/с.
§
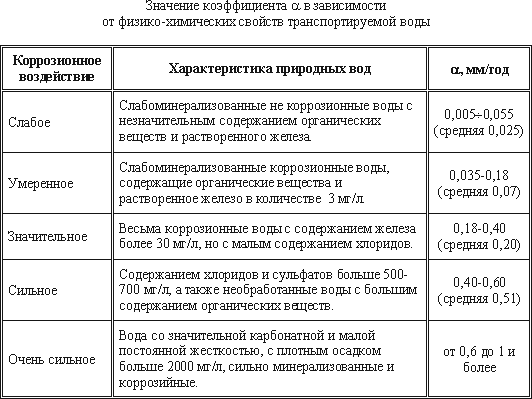
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:
kt = k0 αt
где k0 – абсолютная шероховатость для новых труб, (мм),
kt – шероховатость через t лет эксплуатации,
α – коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
Таблица 6.1
ГИДРАВЛИЧЕСКИЕ МАШИНЫ
Гидравлическими машинами называются машины, которые сообщают протекающей через них жидкости механическую энергию (насос), либо получают от жидкости часть энергии и передают ее рабочему органу для полезного использования (гидродвигатель).
Насосы и гидромоторы применяют также в гидропередачах, назначением которых является передача механической энергии от двигателя к исполнительному органу, а также преобразование вида и скорости движения последнего посредством жидкости.
Гидропередачи по сравнению с механическими передачами (муфты, коробки скоростей, редукторы и т.д.) имеют следующие преимущества
1. Плавность работы.
2. Возможность бесступенчатого регулирования скорости.
3. Меньшая зависимость момента на выходном валу от нагрузки, приложенной к исполнительному органу.
4. Возможность передачи больших мощностей.
5. Малые габаритные размеры.
6. Высокая надежность.
Эти преимущества привели к большому распространению гидропередач, несмотря на их несколько меньший, чем у механических передач КПД.
Лопастные насосы
В современной технике применяется большое количество разновидностей машин. Наибольшее распространение для водоснабжения населения получили лопастные насосы. Рабочим органом лопастной машины является вращающееся рабочее колесо, снабженное лопастями. Лопастные насосы делятся на центробежные и осевые.
В центробежном лопастном насосе жидкость под действием центробежных сил перемещается через рабочее колесо от центра к периферии.
На рисунке 7.1 изображена простейшая схема центробежного насоса. Проточная часть насоса состоит из трех основных элементов – подвода 1, рабочего колеса 2 и отвода 3. По подводу жидкость подается в рабочее колесо из подводящего трубопровода. Рабочее колесо 2 передает жидкости энергию от приводного двигателя. Рабочее колесо состоит из двух дисков а и б, между которыми находятся лопатки в, изогнутые в сторону, противоположную направлению вращения колеса. Жидкость движется через колесо из центральной его части к периферии. По отводу жидкость отводится от рабочего колеса к напорному патрубку или, в многоступенчатых насосах, к следующему колесу.
В осевом лопастном насосе жидкость перемещается в основном вдоль оси вращение рабочего колеса (рисунок 7.2). Рабочее колесо осевого насоса похоже на винт корабля. Оно состоит из втулки 1, на которой закреплено несколько лопастей 2. Отводом насоса служит осевой направляющий аппарат 3, с помощью которого устраняется закрутка жидкости, и кинетическая энергия ее преобразуется в энергию давления. Осевые насосы применяют при больших подачах и малых давлениях.
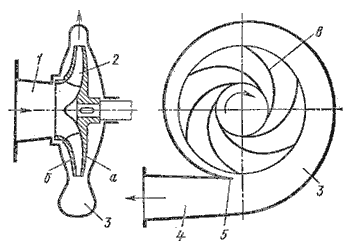
Рисунок 7.1 – Схема центробежного насоса
В осевом лопастном насосе жидкость перемещается в основном вдоль оси вращение рабочего колеса (рисунок 7.2). Рабочее колесо осевого насоса похоже на винт корабля. Оно состоит из втулки 1, на которой закреплено несколько лопастей 2. Отводом насоса служит осевой направляющий аппарат 3, с помощью которого устраняется закрутка жидкости, и кинетическая энергия ее преобразуется в энергию давления. Осевые насосы применяют при больших подачах и малых давлениях.
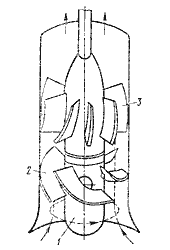
Рисунок 7.2 – Схема осевого насоса
Осевые насосы могут быть жестколопастными, в которых положение лопастей рабочего колеса не изменяется, и поворотно-лопастными, в которых положение рабочего колеса может регулироваться.
Поршневые насосы
Поршневые насосы относятся к числу объемных насосов, в которых перемещение жидкости осуществляется путем ее вытеснения из неподвижных рабочих камер вытеснителями. Рабочей камерой объемного насоса называют ограниченное пространство, попеременно сообщающееся со входом и выходом насоса. Вытеснителем называется рабочий орган насоса, который совершает вытеснение жидкости из рабочих камер (плунжер, поршень, диафрагма).
Классифицируются поршневые насосы по следующим показателям:
1) по типу вытеснителей: плунжерные, поршневые и диафрагменные;
2) по характеру движения ведущего звена: возвратно-поступательное движение ведущего звена; вращательное движение ведущего звена (кривошипные и кулачковые насосы);
3) по числу циклов нагнетания и всасывания за один двойной ход: одностороннего действия; двухстороннего действия.
4) по количеству поршней: однопоршневые; двухпоршневые; многопоршневые.
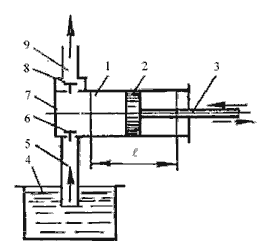
Рисунок 7.3 – Насос поршневой простого действия
Насос простого действия. Схема насоса простого действия изображена на рисунке 7.3. Поршень 2 связан с кривошипно-шатунным механизмом через шток 3, в результате чего он совершает возвратно-поступательное движение в цилиндре 1. Поршень при ходе вправо создает разрежение в рабочей камере, вследствие чего всасывающий клапан 6 поднимается и жидкость из расходного резервуара 4 по всасывающему трубопроводу 5 поступает в рабочую камеру 7. При обратном ходе поршня (влево) всасывающий клапан закрывается, а нагнетательный клапан 8 открывается, и жидкость нагнетается в напорный трубопровод 9.
Так как каждому обороту двигателя соответствует два хода поршня, из которых лишь один соответствует нагнетанию, то теоретическая производительность в одну секунду будет:
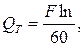 (7.1)
(7.1)
где F – площадь поршня, м²;
l – ход поршня, м;
n – число оборотов двигателя, об/мин.
Для повышения производительности поршневых насосов их часто выполняют сдвоенными, строенными и т.д. Поршни таких насосов приводятся в действие от одного коленчатого вала со смещением колен.
Действительная производительность насоса Q меньше теоретической, так как возникают утечки, обусловленные несвоевременным закрытием клапанов, неплотностями в клапанах и уплотнениях поршня и штока, а также неполнотой заполнения рабочей камеры. Отношение действительной подачи Q к теоретической QT называется объемным КПД поршневого насоса:
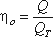 (7.2)
(7.2)
Объемный КПД – основной экономический показатель, характеризующий работу насоса.
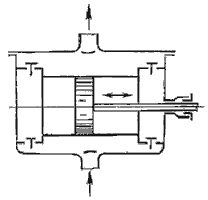
Рисунок 7.4 – Насос поршневой двойного действия
Насос двойного действия. Более равномерная и увеличенная подача жидкости, по сравнению с насосом простого действия, может быть достигнута насосом двойного действия (рисунок 7.4), в котором каждому ходу поршня соответствуют одновременно процессы всасывания и нагнетания. Эти насосы выполняются горизонтальными и вертикальными, причем последние наиболее компактны. Теоретическая производительность насоса двойного действия будет:
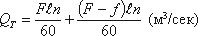
где f – площадь штока, м2.
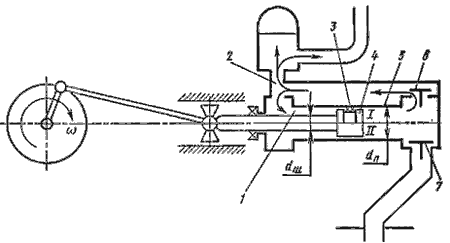
Рисунок 7.5 – Схема поршневого насоса с дифференциальным поршнем
Дифференциальный насос. В дифференциальном насосе (рисунок 7.5) поршень 4 перемещается в гладко обработанном цилиндре 5. Уплотнением поршня служит сальник 3 (вариант I ) или малый зазор (вариант II ) со стенкой цилиндра. Насос имеет два клапана: всасывающий 7 и нагнетательный 6, а также вспомогательную камеру 1. Всасывание происходит за один ход поршня, а нагнетание за оба хода. Так, при ходе поршня влево из вспомогательной камеры в нагнетательный трубопровод 2 вытесняется объем жидкости, равный (F – f )l; при ходе поршня вправо из основной камеры вытесняется объем жидкости, равный fl. Таким образом, за оба хода поршня в нагнетательный трубопровод будет подан объем жидкости, равный
(F – f)l fl = Fl
т.е. столько же, сколько подается насосом простого действия. Разница лишь в том, что это количество жидкости подается за оба хода поршня, следовательно, и подача происходит более равномерно.
§
Баланс мощности в насосе наглядно можно представить в виде схемы, представленной на рисунке 7.7.
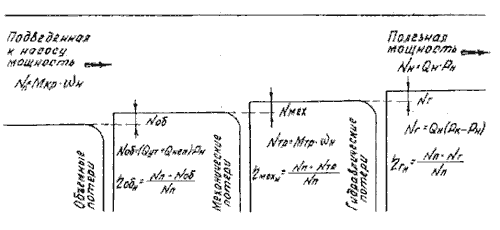
Рисунок 7.7 – Баланс мощности насоса
Мощность, которая подводится к валу насоса называется подведенной. Она равна произведению крутящего момента на валу на его угловую скорость:
NП = MКРω (7.3)
Мощность, которую мы получаем от насоса в виде потока жидкости под давлением называется полезной мощностью насоса (в дальнейшем просто мощностью):
NП = QHPH (7.4)
Отношение мощности насоса к подведенной мощности называется общим КПД насоса:
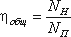
разность NП – NH = Nпот называется потерями мощности в насосе. Потери мощности в насосе делятся на объемные, механические и гидравлические.
Потери мощности на внутренние утечки и неполное заполнение камер насоса:
Nоб = (Qут Qнеп)PH
Объемный КПД насоса определится из соотношения:
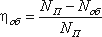
Для современных насосов объемный КПД находится в пределах 0,92…0,96. Значения КПД приведены в технических характеристиках насосов.
Механические КПД характеризует потери на терние в подвижных соединениях между деталями насоса. При относительном перемещении соприкасающихся поверхностей в зоне их контакта всегда возникает сила трения, которая направлена в сторону, противоположную движению. Эта сила расходуется на деформацию поверхностного слоя, пластическое оттеснение и на преодоление межмолекулярных связей соприкасающихся поверхностей.
Мощность, затраченная на преодоление сил трения, определяется по формуле
Nтр = Mтрω, (7.5)
где Мтр – момент трения в насосе;
ω – угловая скорость вала насоса.
Механический КПД определяется из соотношения:
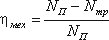
Для современных насосов механический КПД также находится в пределах 0,92…0,96.
Гидравлический КПД характеризует потери на деформацию потока рабочей жидкости в напорной камере и на трение жидкости о стенки сосуда. Эти потери примерно на порядок ниже механических потерь на трение и часто в инженерных расчетах не учитываются или объединяются с механическими потерями на трение. В этом случае объединенный КПД называется гидромеханическим.
Мощность, затраченная на гидравлические потери, определится
Nг = QH ( PK – PH ), (7.6)
где PК – давление в напорной камере насоса;
PН – давление в напорной гидролинии на выходе из насоса.
Гидравлический КПД определяется из соотношения:
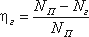
Общий КПД насоса равен произведению КПД объемного, гидравлического и механического
η = ηоб ηмех ηг
Таким образом, баланс мощности насоса дает представление о потерях, возникающих в насосе, общем КПД и всех его составляющих.
§
Кроме насосов и гидромоторов существуют и другие разнообразные по конструкции и назначению гидроэлементы. Одни управляют потоком рабочей жидкости, другие служат для обеспечения безотказной работы гидросистем и т.д. Совокупность этих устройств называется гидроприводом и требует отдельного изучения. Все гидроэлементы имеют свое условное обозначение, из которых составляются гидросхемы по аналогии с электрическими схемами.
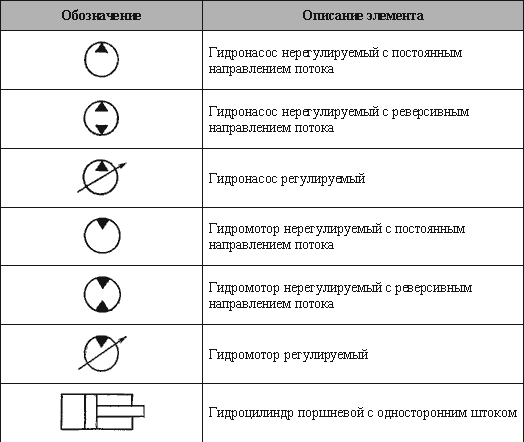
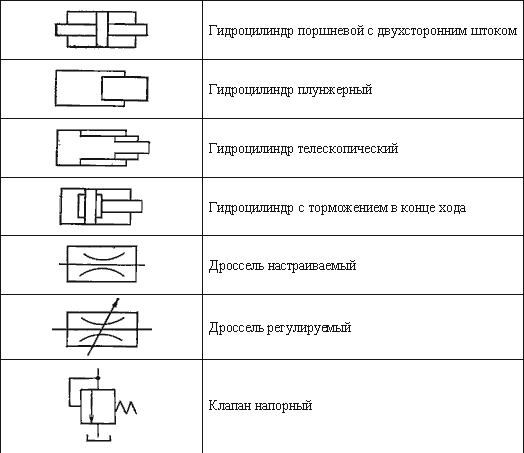
Ниже приводятся условные обозначения основных гидроэлементов.
Таблица 7.1 – Условные обозначения основных гидроэлементов
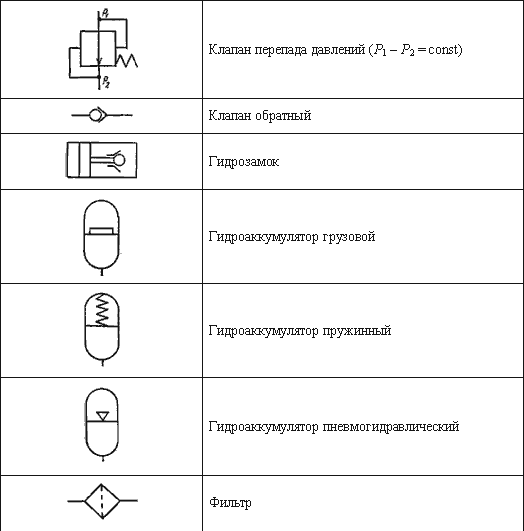
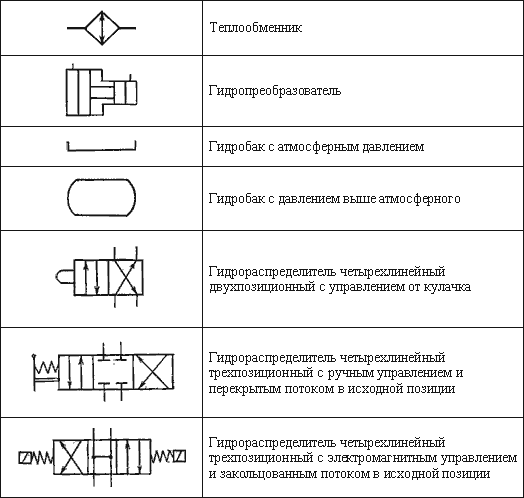
На рисунке 7.8 изображен составленный из условных обозначений пример гидравлической схемы привода поворота стрелы челюстного погрузчика.
Схема состоит из бака, нерегулируемого гидромотора, трехпозиционного гидрораспределителя, двух регулируемых дросселей с параллельно подключенными к ним обратными клапанами, двух гидроцилиндров, фильтра и предохранительного клапана.
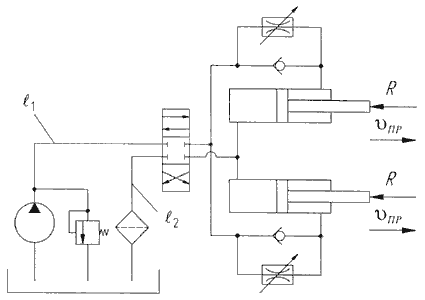
Рисунок 7.8 – Гидросхема привода поворота стрелы
Принцип работы гидропривода заключается в следующем. Из бака рабочая жидкость (масло) забирается насосом и подается к гидрораспределителю. В нейтральном положении золотника гидрораспределителя при работающем насосе на участке трубопровода между насосом и распределителем начинает увеличиваться давление, при этом срабатывает предохранительный клапан и жидкость сливается обратно в бак. При смене позиции золотника (нижняя позиция на схеме) открываются проходные сечения в гидрораспределителе, и жидкость начинает поступать в полости нагнетания гидродвигателей (поршневые полости гидроцилиндров). Из штоковой полости гидроцилиндров масло по гидролинии слива проходит через регулируемые дроссели, гидрораспределитель и, очищаясь фильтром, попадает на слив в бак. Скорость поступательного движения штоков гидроцилиндров регулируется дросселями. Реверсирование движения штоков осуществляется путем переключения позиций гидрораспределителя. При обратном движении штоков без нагрузки их скорость не регулируется и зависит от расхода рабочей жидкости в штоковые полости. При аварийной остановке штоков (например, непреодолимое усилие) давление в системе возрастает, вызывая тем самым открытие предохранительного клапана и сброс рабочей жидкости в бак.








