Блок 5. режимы
движения жидкости и лабораторная работа №5
1.
Поясните физическую сущность ламинарного и турбулентного режимов
движения жидкости.
При
ламинарном движении жидкость в процессе движения не перемешивается, а при
турбулентном движении перемешивается.
2.
Для чего употребляется число Рейнольдса в гидравлических расчетах?
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю.
Измерение давлений (удельных энергий) в потоке
В ПОТОКЕ
Удельные механические энергии в потоке движущейся жидкости, представленные в уравнении Бернулли (1.32)-(1.32в), могут быть непосредственно измерены относительно простыми средствами.
На рис. 1.9 показаны способы измерения статического (Лст = = PcJpg) и суммарного статического и скоростного (Лст hCK = = PcJpg w2/2g) напоров, пропорциональных удельной энергии статического сжатия и суммарной удельной энергии статического сжатия и кинетической энергии соответственно.
Измерительные устройства представляют собой трубочки относительно малого диаметра (обычно это тонкостенные трубочки диаметром несколько миллиметров). В трубочке, вставленной в стенку трубопровода перпендикулярно направлению движения потока, жидкость поднимается на высоту,

Рис. 1.9. Измерение статического и полного напоров в потоке равную статическому напору hCT. При этом важно, чтобы конец измерительной трубочки был вставлен в стенку трубопровода заподлицо, без каких-либо выступов, которые могли бы вызвать местное (локальное) возмущение потока и исказили бы измеряемую величину статического напора; поток не должен «ощущать» наличия измерительной трубочки в стенке трубопровода.
Суммарный, т. е. статический плюс скоростной (динамический), напор измеряется с помощью аналогичной трубочки, но расположенной одним из открытых концов навстречу потоку. Такая трубка воспринимает от потока не только статический, но одновременно и скоростной напор (Лск), т. е. величину hCT hCK, поскольку та струйка потока, которая набегает на открытый конец измерительной трубки, теряет свою скорость, и ее удельная кинетическая энергия движения локально превращается в дополнительную (к имеющейся статической энергии сжатия в потоке) статическую энергию, воспринимаемую жидкостью внутри изогнутой измерительной трубки.
Значения измеренных таким образом статического и суммарного (полного) напоров могут быть пересчитаны в соответствующие давления:

Вычисленные значения статического и полного напоров дают возможность определить величину скоростного давления

откуда находится локальная скорость потока:

Скорость можно вычислить и непосредственно через измеренные значения статического и полного напоров:

откуда
Понятие об удельной энергии
Удельная энергия – энергия, приходящаяся на единицу силы тяжести. Обозначая энергию буквой Е, силу тяжести буквой G, для удельной энергии е получим
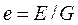 (32)
(32)
Размерность удельной энергии [ м ], т. е. удельная энергия измеряется единицами длины.
Энергия жидкости разделяется на энергию положения, энергию давления и кинетическую энергию.
Подсчитаем удельную энергию для частицы жидкости.
Удельная энергия положения. Возьмем сосуд, наполненный жидкостью (рис. 21). Определим энергию положения жидкой частицы в точке А с координатой z. Если сила тяжести частицы G=mg, то ее энергия положения над плоскостью X-X будет Епол = Gz, а удельная энергия положения
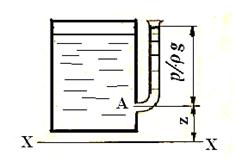
Рис. 21.
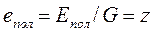
Удельная энергия положения равна геометрической высоте точки над координатной плоскостью.
Удельная энергия давления. Частица жидкости в точке А (рис. 21) находится под давлением окружающей жидкости, поэтому если от уровня этой точки вывести пьезометр, то частица может в нем подняться на высоту  [см. формулу (16)]. Следовательно, энергия давления
[см. формулу (16)]. Следовательно, энергия давления
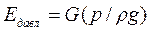
Соответственно, удельная энергия давления
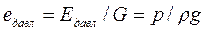
Сумма удельной энергии давления и удельной энергии положения называется удельной потенциальной энергией
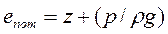 (33)
(33)
Из рис.21 следует, что для любой частицы жидкости удельная потенциальная энергия равна расстоянию от плоскости сравнения X-X до уровня жидкости в пьезометре.
Удельная кинетическая энергия. Подсчитаем величину удельной кинетической энергии жидкой частицы массой т. Кинетическая энергия, как известно, может быть выражена формулой
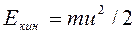
где u – скорость частицы. Удельная кинетическая энергия
 (34)
(34)
Величину  можно измерить, если опустить в движущуюся жидкость (рис. 22) трубку, изогнутую в направлении, противоположном движению. Тогда уровень жидкости в трубке поднимется выше уровня свободной поверхности потока на (
можно измерить, если опустить в движущуюся жидкость (рис. 22) трубку, изогнутую в направлении, противоположном движению. Тогда уровень жидкости в трубке поднимется выше уровня свободной поверхности потока на (  ), так как движущаяся жидкость будет оказывать дополнительное давление, равное (
), так как движущаяся жидкость будет оказывать дополнительное давление, равное (  ).
).
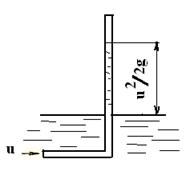
Рис.22
Такая трубка называется трубкой Пито (1695-1771 гг.), предложившего ее в 1732 г. для измерения скорости жидкости.
Вместо термина «удельная энергия» очень часто употребляют термин «напор». Удельную кинетическую энергию называют скоростным напором, а удельную потенциальную энергию – пьезометрическим или гидростатическим напором.
Дата добавления: 2021-04-18; просмотров: 29; Нарушение авторских прав
§
§
Пусть частица жидкости (рис. 25) движется от точки 1 в сечении А-Адо точки 2 в сечении В–В. Подсчитаем удельную энергию, которой обладает частица в точках 1 и 2. Обозначим u1, p1 скорость частицы и давление в точке 1 с координатой zl а u2, р2 — скорость частицы и давление в точке 2 с координатой z2. При этих обозначениях для частицы в сечении А-А:
z1 – удельная энергия положения; ( 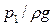 )- удельная энергия давления; (
)- удельная энергия давления; ( 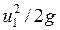 ) – удельная кинетическая энергия.
) – удельная кинетическая энергия.
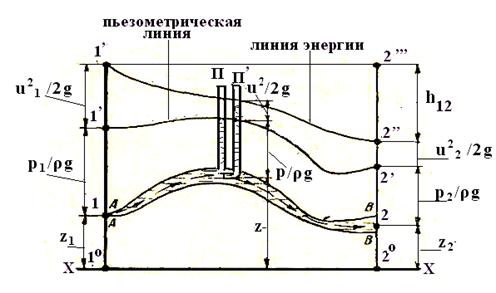
Рис.25.
Для частицы в сечении В-В:
z2 – удельная энергия положения;  – удельная энергия давления;
– удельная энергия давления; 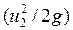 -удельная кинетическая энергия.
-удельная кинетическая энергия.
Полная удельная энергия частицы в сечении А-А,очевидно, равна
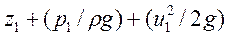 (37)
(37)
а в сечении В–В
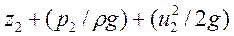 (38)
(38)
Для частицы идеальной жидкости полная удельная энергия остаётся постоянной величиной. Для частицы реальной жидкости трехчлен (37) больше трехчлена (38), так как на пути 1-2 часть энергии израсходуется на преодоление различных сопротивлений. Эта часть удельной энергии называется потерей напора и обозначается буквой h1-2. Тогда на основании закона о сохранении энергии можно написать
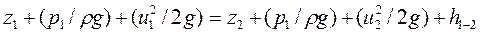 (39)
(39)
Уравнение (39) называется уравнением Даниила Бернулли для частицы жидкости. Все члены этого уравнения имеют размерность длины, и поэтому его можно изобразить графически (рис 25). Откладывая в каждой точке отрезка 1o-2o оси А последовательно координаты частицы жидкости z, высоты p/ρg и скоростные высоты u2/2g, получим линии 1-2, 1′-2’и 1”-2”. Линия 1-2 – это траектория движения частицы жидкости, линия 1′-2′, называемая пьезометрической линией, показывает изменение удельной потенциальной энергии z p/ρg, а линия 1”-2” – изменение полной удельной энергии частицы и носит название линии энергии. Все эти линии в общем
случае будут кривыми, причем линия энергии может только
опускаться так как энергия в направлении движения
уменьшается.
Проведя горизонтальную прямую 1”-2”’, получим для сечения В-В отрезок 2″-2′”,который равен потере напора h1-2на пути 1-2, а вертикальные отрезки между прямой 1″-2′”и линией энергии 1”-2” представляют собой потери напора на участке от сечения А-Адо рассматриваемого сечения.
В заключение отметим, что величины z p/ρg и u2/2g можно измерить, поставив пьезометр П и изогнутую трубку П'(рис.26). В пьезометре Пжидкость поднимается до пьезометрической линии, а в трубке П’ – до линии энергии. Разность уровней в П и П’ даст величину u2/2g.
Дата добавления: 2021-04-18; просмотров: 6; Нарушение авторских прав
§
Уравнение Даниила Бернулли легко распространить и на поток жидкости (рис. 26) при условии, что в живых сечениях, для которых применено это уравнение, движение плавноизменяющееся.
Рассмотрим напорный поток 1-2(рис. 26). Пусть жидкость движется от живого сечения 1 до живого сечения 2, а площади этих живых сечений равны ω1 и ω2. Подсчитаем полную удельную энергию потока для сечения 1.
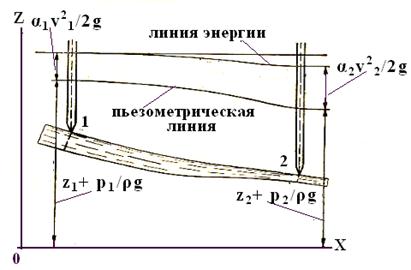
Рис.26
Удельная потенциальная энергия жидкости во всех точках сечения 1-2 величина постоянная и равна вертикальному расстоянию от плоскости сравнения X (рис. 26) до свободной поверхности (до уровня) жидкости в пьезометре. Удельную потенциальную энергию жидкости для сечения 1обозначим z1 p1/ρg .
Удельная кинетическая энергия жидкости, протекающей через живое сечение, может быть выражена через среднюю скорость при условии введения некоторого коэффициента. Этот коэффициент в гидравлике обозначается α и называется коэффициентом Кориолиса. Следовательно, удельная кинетическая энергия для сечения равна 
Таким образом, полная удельная энергия для сечения 1 составляет
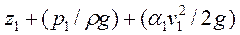 (40)
(40)
Совершенно аналогично для сечения 2 полная удельная энергия равна
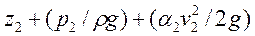 (41)
(41)
Для потока идеальной жидкости полная удельная энергия потока остаётся неизменной. Для реальной жидкости трехчлен (40) больше трехчлена (41), так как на пути от сечения 1 до сечения 2часть энергии израсходуется на преодоление различных сопротивлений. Обозначая потерянную удельную энергию (потерю напора) буквой h1-2 можем написать
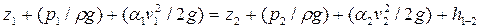 (42)
(42)
Уравнение (42) называется уравнением Даниила Бернулли для потока. Коэффициент Кориолиса α, представляющий собой отношение действительной кинетической энергии к кинетической энергии, вычисленной при условии движения всех частиц в сечении с одной и той же скоростью. Опыты показывают, что α обычно изменяется в пределах от 1,03 до 1,1.
Поскольку коэффициент α близок к единице, то очень часто полагают α = 1, и тогда уравнение Бернулли для потока принимает вид
 (41)
(41)
Следует отметить, что удельная потенциальная энергия  равна расстоянию от плоскости сравнения X до уровня жидкости в пьезометре только в том случае, когда давление в сечении изменяется по гидростатическому закону. Если же давление в сечении изменяется не по гидростатическому закону, то удельная потенциальная энергия не равна расстоянию от плоскости сравнения до уровня жидкости в пьезометре. Так, например, если давление по всему живому сечению равно барометрическому (для всех точек живого сечения манометрическое давление р = 0), то в этом случае удельная потенциальная энергия равна удельной энергии положения, т. е. расстоянию от плоскости сравнения до центра тяжести потока. Для потока (рис. 27), так же как и для частицы, линия, показывающая изменение удельной потенциальной энергии
равна расстоянию от плоскости сравнения X до уровня жидкости в пьезометре только в том случае, когда давление в сечении изменяется по гидростатическому закону. Если же давление в сечении изменяется не по гидростатическому закону, то удельная потенциальная энергия не равна расстоянию от плоскости сравнения до уровня жидкости в пьезометре. Так, например, если давление по всему живому сечению равно барометрическому (для всех точек живого сечения манометрическое давление р = 0), то в этом случае удельная потенциальная энергия равна удельной энергии положения, т. е. расстоянию от плоскости сравнения до центра тяжести потока. Для потока (рис. 27), так же как и для частицы, линия, показывающая изменение удельной потенциальной энергии  называется пьезометрической линией, а линия, показывающая изменение полной удельной энергии, – линией энергии.
называется пьезометрической линией, а линия, показывающая изменение полной удельной энергии, – линией энергии.
Дата добавления: 2021-04-18; просмотров: 7; Нарушение авторских прав
§
§
Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потеря напора определяется лишь потерей по длине.
Выделим из потока участок жидкости (рис. 29) длиной L и напишем уравнение Бернулли для сечений 1 и 2.
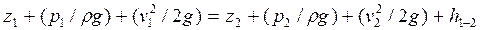 (46)
(46)
где z1 , z2 – ординаты центра тяжести сечений 1 и 2; p1 и р2 – давления в центрах тяжести этих сечений; v1 и v2 – средние скорости в этих сечениях;
h1-2 – потеря напора по длине.
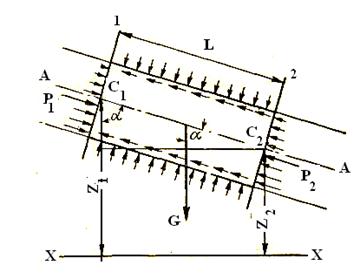
Рис.29
Так как движение равномерное, то v1 = v2 и уравнение (46) можно переписать так:
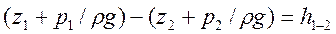 (47)
(47)
т.е. в случае равномерного движения разность удельных потенциальных энергий равна потере напора по длине. Для вычисления этой разности напишем сумму проекций на ось потока А-Авсех сил, действующих на участке 1-2. Эта сумма должна равняться нулю, так как при равномерном движении все силы уравновешиваются. Эти силы следующие:
1) сила тяжести жидкости 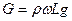 , где ω=ω1= ω2 – площади живых сечений;
, где ω=ω1= ω2 – площади живых сечений;
2) силы давления на плоские сечения ω1 и ω2, равные Р1= р1ω1 и Р2 = р2ω2;
3) силы давления на боковую поверхность;
4) сила трения  ; где τ – сила трения на единицу площади боковой поверхности цилиндра, а χ -смоченный периметр.
; где τ – сила трения на единицу площади боковой поверхности цилиндра, а χ -смоченный периметр.
Спроектируем все эти силы на ось А-А:
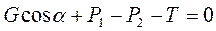 (48)
(48)
Из рисунка 29 видно 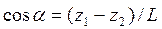 . Подставив значения сил в (48), получим
. Подставив значения сил в (48), получим
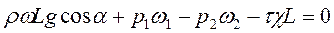
Разделим обе части этого равенства на ρωLg:
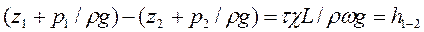 (49)
(49)
Откуда
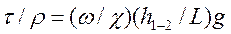 (50)
(50)
Имея в виду, что (ω/χ)= R, a ( h1-2/L)= i, из уравнения (50) получим
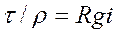 (51)
(51)
Уравнение (51) называется основным уравнением равномерного движения.
Величина gRi имеет размерность квадрата скорости. Величина 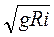 называется динамической скоростью и для краткости обозначается
называется динамической скоростью и для краткости обозначается 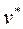 , т. е.
, т. е.
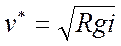 (52)
(52)
Дата добавления: 2021-04-18; просмотров: 4; Нарушение авторских прав
§
В 1883 г. английским ученым Осборном Рейнольдсом (1842—1912 гг.) было установлено, что критерием режима течения жидкости является безразмерная величина, представляющая собой отношение произведения средней скорости потока v и линейного размера l, характерного для рассматриваемого случая, к кинематическому коэффициенту вязкости жидкости ν, т. е. величина
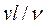
Этот критерий режима течения жидкости в честь Рейнольдса называется числом Рейнольдса и часто обозначается двумя буквами Re.
При напорном движении жидкости в круглых трубах за характерный размер l обычно принимается внутренний диаметр трубы D, а в остальных случаях гидравлический радиус R.
Опытами установлено, что ламинарный режим устойчив в том случае, когда Re≤2320.
Переход из ламинарного в турбулентный режим зависит (помимо скорости движения, вязкости жидкости и размеров живого сечения потока) от ряда факторов, а именно: от возмущений, создаваемых у источника питания потока, от шероховатости стенок русла, от сотрясений русла потока и т. д. В лабораторных условиях удавалось сохранять ламинарный режим при числах Рейнольдса, превышающих 2320. Однако ламинарный режим при этом неустойчив и легко переходит в турбулентный.
На практике ламинарный режим встречается:
а) при движении очень вязкой жидкости;
б) при движении жидкости в капиллярных трубках;
в) при движении воды в грунтах.
Турбулентный режим наблюдается значительно чаще, а именно: при движении воды в реках и каналах, при движении жидкости в трубах и в других случаях.
Дата добавления: 2021-04-18; просмотров: 10; Нарушение авторских прав
§
Возьмем круглую трубу радиусом r (рис. 31). Определим скорость и в произвольно взятой точке М, отстоящей от оси трубы на расстоянии у. Проведем через точку М радиусом, равным y концентрическую поверхность. Основное уравнение равномерного движения (51) для жидкости, движущейся внутри проведенной концентрической поверхности, дает
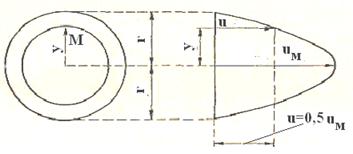
Рис.31
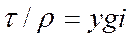 (53)
(53)
(так как гидравлический радиус R = у/2)
Сила трения на единицу площади

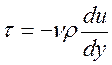 (54)
(54)
где знак минус взят из-за того, что скорость, как показывает опыт, убывает от оси трубы к стенкам, и, следовательно, градиент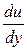 отрицателен. Подставив значение τ в формулу (53), получим
отрицателен. Подставив значение τ в формулу (53), получим
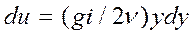
После интегрирования
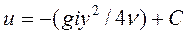 (55)
(55)
Постоянную С определим из условия, что при у= r скорость и= 0, так как частицы жидкости, смачивая стенку, прилипают к ней, т. е. имеют нулевую скорость.
Подставив в формулу (53) эти значения, будем иметь
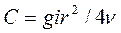
Подставив это значение С в уравнение (55), получим
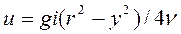 (56)
(56)
Из формулы (54) следует, что скорости при ламинарном режиме распределяются по параболическому закону.
Максимальная скорость, очевидно, получится при значении у = 0, т. е. на оси

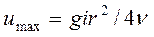
Дата добавления: 2021-04-18; просмотров: 13; Нарушение авторских прав
§
При турбулентном течении в любой точке пространства, занятого жидкостью, мгновенная скорость движения частиц жидкости, проходящих через эту точку, стечением времени изменяется как по величине, так ипо направлению. Явление быстрых изменений мгновенной скорости во времени называется пульсацией скорости.
Рассмотрим изменение ип – проекции мгновенной скорости на ось потока. Ее изменение во времени можно изобразить графически, откладывая иппо оси ординат, а время t по оси абсцисс (рис. 32).
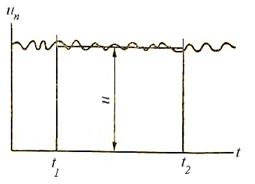
Рис.32
Вместо переменных во времени мгновенных продольных скоростей ипв уравнения движения турбулентных потоков вводится среднее значение и этих скоростей (рис.32) за достаточно длительный промежуток времени (t2– t1)т. е.
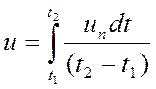
Скорость и называется местной скоростью.
Определенный интеграл, входящий в формулу, выражает площадь, заключенную между пульсационной кривой, осью абсцисс и двумя ординатами, соответствующими начальному t1и конечному t2 моментам наблюдения. Следовательно, местная скорость и представляет собой высоту прямоугольника, равновеликого этой площади.
Время (t2 – t1) должно быть достаточно продолжительным с тем, чтобы получающаяся скорость и мало отличалась от скорости, найденной при очень длительном наблюдении. Необходимую продолжительность наблюдения можно установить лишь опытным путем. Так, при определении скоростей в реках и каналах на измерение скорости вблизи дна вследствие значительной пульсации затрачивается около 5 минут, а у поверхности воды, где пульсация меньше, – около 2 минут.
Дата добавления: 2021-04-18; просмотров: 6; Нарушение авторских прав
§
На рис. 33 показана эпюра распределения местных скоростей в круглой трубе при турбулентном режиме. Из рисунка видно, что скорости весьма быстро возрастают в прилегающем к стенке слое, а затем дальнейшее их
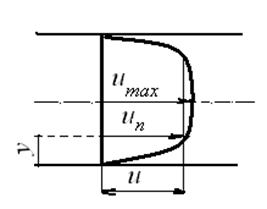
Рис.33
увеличение до максимального значения иmaxпроисходит очень медленно.
В отличие от ламинарного потока, характеризующегося большой неравномерностью параболической эпюры скоростей (рис. 32) с отношением v/umax= 0,5, в турбулентном потоке, как показывают измерения, это отношение не менее 0,75.
Согласно теории, разработанной немецким ученым Людвигом Прандтлем (1875-1953 гг.), местная скорость и в какой-либо точке турбулентного потока (рис.33) определяется по формуле
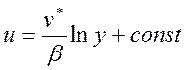 (59)
(59)
где  – динамическая скорость;
– динамическая скорость;
β – некоторый постоянный коэффициент;
у – расстояние от стенки до рассматриваемой точки.
Последняя формула представляет собой логарифмический закон распределения скоростей в турбулентных потоках. Он хорошо подтверждается экспериментами. Только в прилегающем к стенке весьма тонком слое, в котором жидкость движется ламинарно, логарифмический закон не применим. Толщина δл этого слоя ничтожно мала, примерно δл = 0,8v/ν.
Дата добавления: 2021-04-18; просмотров: 8; Нарушение авторских прав
§
До настоящего времени основные зависимости для турбулентного течения теоретически еще не выведены. Как показывают опыты, при турбулентном течении с достаточной точностью для многих случаев практики можно считать, что τ прямо пропорционально квадрату скорости v. Из основного уравнения равномерного движения жидкости видно, что в этих случаях v2прямо пропорционально i или v прямо пропорционально 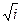 , т. е.
, т. е.

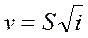 (60)
(60)
Величина S называется скоростной характеристикой. Размерность S та же, что и скорости, т. е. [м/сек]. Формула (60) является основной формулой для определения потерь напора по длине при турбулентном режиме.
Из формулы (60) получаем выражение для гидравлического уклона
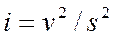 (61)
(61)
Пользуясь формулой (59) и зависимостью 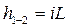 , находим
, находим
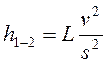 (62)
(62)
Подставив v по формуле (58) в зависимость Q =vω, имеем
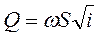
Произведение ωS обозначим К. Тогда
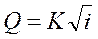 (63)
(63)
Величина К называется расходной характеристикой. Размерность К та же, что и расхода, т. е. [ м3/сек]. Из формулы (63) имеем
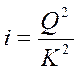 (64)
(64)
Так как h1-2= iL, то, пользуясь формулой (61), получаем
 (65)
(65)
Дата добавления: 2021-04-18; просмотров: 3; Нарушение авторских прав
§
Изучение турбулентного течения показало, что к стенке русла примыкает заторможенный ею весьма тонкий слой жидкости, называемый пограничным слоем. В этом слое вязкость жидкости оказывает значительное влияние на величину и распределение местных скоростей.
Толщина пограничного слоя δ и может быть рассчитана по формуле 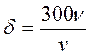 .
.
Пограничный слой состоит из двух слоев: из прилегающего к стенке ламинарного слоя толщиной δл и переходного слоя от ламинарного к турбулентному. Прилегающий к стенке ламинарный слой нередко называют ламинарным подслоем.
Если высота выступов шероховатости Δ на стенках русла (рис.34а) значительно меньше толщины пограничного слоя δ, шероховатость не сказывается на величине скоростной характеристики S. В этом случае русла называются гидравлически гладкими.
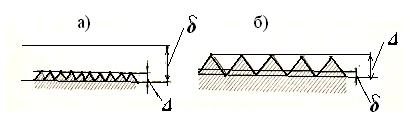
Рис.34
Для этих русел с большой точностью скоростная характеристика определяется из формулы проф. П. К. Конакова
 (68)
(68)
где R – гидравлический радиус; ν – кинематический коэффициент вязкости.
Если же толщина пограничного слоя δ (рис.34б) значительно меньше высоты выступов Δ, скоростная характеристика зависит от шероховатости и не зависит от вязкости и скорости. В этом случае русла называются
гидравлически шероховатыми. Для этих русел с большой точностью скоростная характеристика определяется из формулы проф. А. В. Теплова
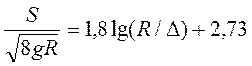 (69)
(69)
где Δ – высота выступов равномерной зернистой шероховатости, эквивалентной по потерям напора данной шероховатости.
Формулы (66) и (67) справедливы для русла любого поперечного сечения. В частном случае, для круглых труб при напорном движении, учитывая, что R = D/4, а 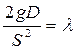 формулы (66) и (67) можно написать в следующем виде
формулы (66) и (67) можно написать в следующем виде
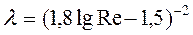 (70)
(70)
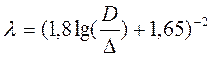 (71)
(71)
На рис. 35 показаны результаты 362 опытов Никурадзе для труб с равномерной зернистой шероховатостью. Прямая А Б, нанесенная на рис. 35, построена по формуле (68), т. е. для гидравлически гладких русел, а горизонтальные прямые (справа от прямой ВГ) – по формуле (69), т. е. для гидравлически шероховатых русел.
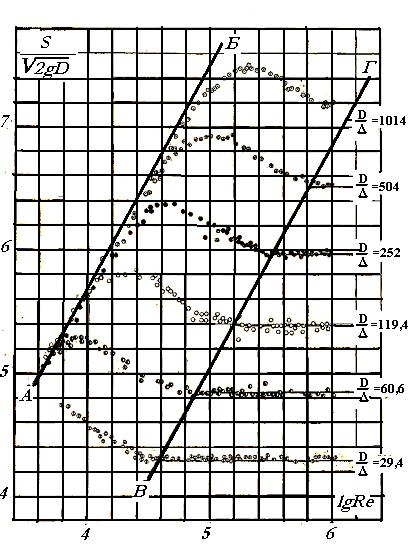
Рис.35
Область, лежащую между АБ и ВГ, называют переходной областью, а область справа от линии ВГ – квадратичной областью (поскольку в ней потери напора прямо пропорциональны квадрату скорости v).
Для труб с равномерной зернистой шероховатостью, согласно опытам, переходная область лежит в границах, определяемых выражением

При определении λ для стальных труб во всех областях турбулентного течения (в том числе и в переходной области) можно применять формулу
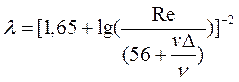 (72)
(72)
ГЛАВА СЕДЬМАЯ
Дата добавления: 2021-04-18; просмотров: 7; Нарушение авторских прав
§
Рассмотрим установившееся движение жидкости на участке горизонтальной трубы (рис. 36), поперечное сечение которой резко увеличивается.
Как показывают опыты, поток при выходе из трубы с
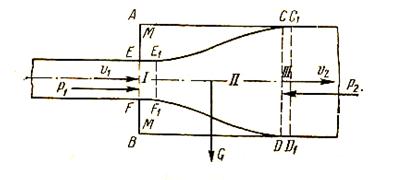
Рис. 36
меньшим диаметром быстро расширяется и в сечении; CD заполняет всю трубу. Между основным потоком и стенками трубы образуется кольцевое пространство ММ, заполненное жидкостью, не участвующей в общем поступательном движении, почему область М нередко называют «мертвым пространством».
При движении жидкости от сечения EF к сечению CD часть энергии жидкости теряется на преодоление сопротивлений. Для определения величины этих потерь выделим из жидкости объем АСDВА и применим к нему теорему о количестве движения, согласно которой при установившемся движении приращение количества движения тела за единицу времени равно сумме проекций (на направление движения) всех действующих на тело сил.
Определим приращение количества движения за единицу времени. За единицу времени через сечение EF, а также и через сечение CD протекает объем жидкости, равный расходу Q, а частицы жидкости, находившиеся в сечениях EF и CD, переместятся соответственно в сечения Е1F1и С1D1Следовательно, жидкость, занимая в первоначальный момент объем ACDBA, через единицу времени будет занимать объем А С1D1В F1F Е1EА.
Для краткости объем жидкости EE1F1FE обозначим римской цифрой I, остальную часть объема ACDBA – цифрой II и объем C С1D1DC – цифрой III. Тогда количество движения в начальный момент равно
к.д.I к.д.II, (73)
а количество движения через единицу времени
к.д.II к.д.III, (74)
Следовательно, для определения приращения количества движения за единицу времени необходимо из выражения (74) вычесть выражение (73). Тогда приращение количества движения за единицу времени составит
к.д.III – к.д.I (75)
Количество движения III равно mv2, где v2 – скорость в сечении CD. Количество движения I равно mv1,где v1 – скорость в сечении EF.
Следовательно, приращение количества движения за единицу времени будет (mv2 – mv1)
Масса mжидкости, протекающей в единицу времени, равна ρQ, или ρωv2, где ω – площадь поперечного сечения трубы большего диаметра. Отсюда получаем, что приращение количества движения за единицу времени равно
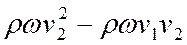 (76)
(76)
Теперь найдем сумму проекций сил на направление движения. На объем ACDBA действуют следующие силы, для которых будем указывать и соответствующие проекции:
1. Сила Р1 на грань АВ. Эта сила равна р1ω, где р1 – давление в центре тяжести сечения АВ. Проекция этой силы на направление движения равна ( р1ω).
2. Сила Р2 на грань CD. Эта сила равна р2ω, где р2 –
давление в центре тяжести сечения CD. Проекция этой
силы на направление движения равна (-р2ω).
3. Реакции боковых стенок на жидкость. Эти силы нормальны к оси трубы, следовательно, их проекция на направление движения равна нулю.
4. Сила тяжести жидкости G в объеме ACDBA. Сила G вертикальна, а поэтому ее проекция на направление движения равна нулю.
5. Силы трения жидкости о поверхность трубы на участке между сечениями АВ и CD.Эти силы, как показывает опыт, малы по сравнению с силами Р1и Р2, а потому ими можно пренебречь.
Таким образом, сумма проекций сил, действующих на объем AСОВА, равна
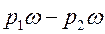 (77)
(77)
На основании теоремы о количестве движения выражение (77) должно равняться выражению (74), т. е.
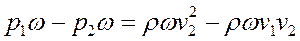 (78)
(78)
Сократив на ω и разделив на ρg левую и правую части выражения (78), получим
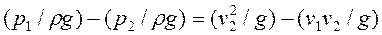 (79)
(79)
Теперь напишем уравнение Бернулли для сечений АВ и CD:
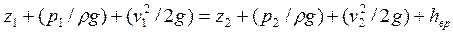 (80)
(80)
где 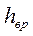 – потери напора при внезапном расширении. Поскольку z1 = z2, выражение (80) можно переписать в следующем виде:
– потери напора при внезапном расширении. Поскольку z1 = z2, выражение (80) можно переписать в следующем виде:
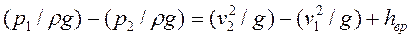 (81)
(81)
В выражениях (79) и (81) левые части равны, следовательно, в них равны и правые части, т. е
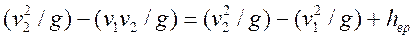

Из этого выражения получаем
 (82)
(82)
Последнее выражение носит название формулы Борда. В частном случае, когда скорость v2мала по сравнению со скоростью v1,
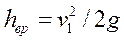
т. е. местные потери напора в этом случае равны удельной кинетической энергии.
Дата добавления: 2021-04-18; просмотров: 5; Нарушение авторских прав
§
Во всех случаях, кроме рассмотренного выше внезапного расширения, местные потери напора определяются по формуле
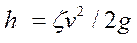 (83)
(83)
где
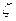 – коэффициент потерь;
– коэффициент потерь;
v – средняя скорость движения жидкости непосредственно за местным сопротивлением.
Коэффициент потерь 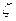 определяется опытным путем и при решении задач берется из справочников.
определяется опытным путем и при решении задач берется из справочников.
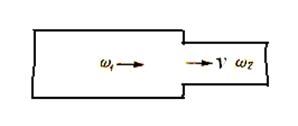
Рис. 37
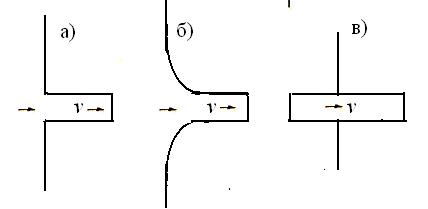
Рис. 38
Ниже приводятся численные значения коэффициента потерь в трубах при турбулентном течении для некоторых случаев.
1. Внезапное сужение (рис. 37, табл. 2).
Таблица 2
| ω1/ω2 | 0,1 и менее | 0,2 | 0,4 | 0,6 | 0,8 |
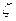 | 0,50 | 0,42 | 0.34 | 0,25 | 0,15 |
В таблие: ω1 – площадь живого сечения в широкой части потока, ω2 – площадь живого сечения в узкой части потока.
2. Вход в трубу:
а) без округления кромки входного отверстия 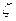 = 0,5 (рис. 38, а);
= 0,5 (рис. 38, а);
б) при плавном входе (в зависимости от плавности 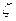 = 0,5÷0,1 (рис. 38.б);
= 0,5÷0,1 (рис. 38.б);
в) если труба вдвинута внутрь резервуара (в зависимости от длины вдвинутой части), 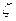 = 0,75÷1,1 (рис. 38.в) .
= 0,75÷1,1 (рис. 38.в) .
3. Колено (плавное закругление, рис. 39, а) с радиусом закругления г и внутренним диаметром D (табл. 3).
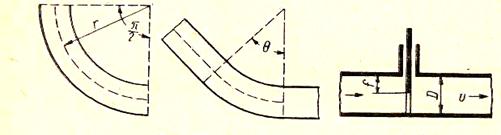
а) б) в)
Рис.39
Таблица 3
| D/r | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 |
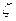 | 0,13 | 0,14 | 0,16 | 0,21 | 0,29 | 0,44 | 0,66 | 0,98 | 1,41 | 1,98 |
В случае если угол поворота не равен л/2, табличная величина 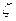 умножается на 2Ө/ л (рис. 39, б).
умножается на 2Ө/ л (рис. 39, б).
4. Задвижка в трубе (рис. 39 в, табл. За). Здесь: f – длина вошедшей в трубу части щита, D – внутренний диаметр.
Таблица 3а
ГЛАВА ВОСЬМАЯ
Дата добавления: 2021-04-18; просмотров: 7; Нарушение авторских прав
§
Рассмотрим движение жидкости в трубопроводе (рис. 40). Составим уравнение Бернулли для сечений 1 и 2:
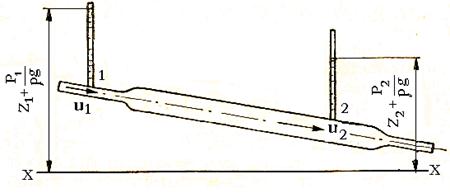
Рис.40
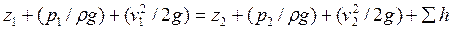
где 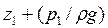 и
и 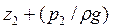 – удельные потенциальные энергии; v1 и v2 – средние скорости; ∑ h – сумма потерь напора между сечениями 1 и 2.
– удельные потенциальные энергии; v1 и v2 – средние скорости; ∑ h – сумма потерь напора между сечениями 1 и 2.
Из этого уравнения получаем
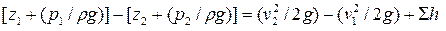 (84)
(84)
Левая часть выражения (84) представляет собой разность отметок линии потенциальной энергии в сечениях 1 и 2, в правой же части величина (v22/2g – v21/2g) является разностью удельных кинетических энергий. Потери напора ∑h, как известно, слагаются из потерь по длине h1-2и местных потерь hм. Поэтому выражение (84) может быть переписано так:
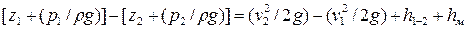 (85)
(85)
Если трубопровод имеет большую длину (более 100 м), то по сравнению с потерями по длине h1-2местные потери hм и разность удельных кинетических энергий представляют незначительную величину, которой обычно пренебрегают.
В этом случае выражение (85) получает вид
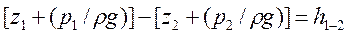
т. е. считается, что разность отметок пьезометрической линии равна потерям напора по длине.
При гидравлическом расчете трубопроводов надо иметь в виду, что трубопровод, как правило, будет существовать долгое время и поэтому трубы со временем покроются осадками, т. е. из новых сделаются старыми. В таком виде трубы должны давать требующееся по расчету количество жидкости. Отсюда следует, что трубы надо рассчитывать как бывшие в употреблении. Поэтому при расчете водопроводов из чугунных и стальных труб обычно принимают Δ= 1 мм, а при расчете канализационной сети Δ= 2 мм.
Дата добавления: 2021-04-18; просмотров: 4; Нарушение авторских прав
§
§
Если при напорном движении жидкости в трубе (рис.43) мгновенно закрыть кран, то движущаяся жидкость остановится, кинетическая энергия потока израсходуется на сжатие жидкости и расширение стенок трубы. Вследствие сжатия жидкости и расширения стенок трубы любое сечение А-А, взятое в жидкости, сместится по направлению движения в положение Б–Б. Аналогичные явления произойдут и со всеми остальными сечениями. Таким образом, вся жидкость в трубе по окончании

Рис.43
деформации окажется сжатой, а поэтому обладающей большей энергией, чем жидкость в баке. В результате этого начнется обратное движение жидкости и сечение Б-Б, пройдя свое первоначальное положение А-А, займет место В-В. Аналогичные движения совершат и все остальные сечения, вследствие чего в трубе создастся пониженное давление и жидкость двинется от сосуда к крану. Затем все явление повторится и будет повторяться снова и снова, пока под влиянием сопротивлений оно постепенно не прекратится.
Итак, частицы жидкости будут совершать затухающие колебания, одновременно с которыми будет изменяться и давление. Изменение давления в жидкости при напорном движении, вызываемое резким изменением скорости течения за весьма малый промежуток времени, называется гидравлическим ударом.
Увеличение давления при гидравлическом ударе может привести к разрыву стенок трубы. Это увеличение давления в первый момент происходит непосредственно у крана, а затем оно передается через соседние слои по всей длине L трубы до ее начала с некоторой скоростью с. Эта скорость носит название скорости распространения ударной волны. По истечении времени 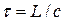 ударная волна дойдет до начала трубы и вся жидкость в трубе остановится.
ударная волна дойдет до начала трубы и вся жидкость в трубе остановится.
Величину повышения давления в трубе при гидравлическом ударе можно определить следующим образом. Обозначим в горизонтальной трубе (рис. 43) давление всечении 1-1 буквой р1 а давление в сечении 2-2 (при гидравлическом ударе) – р2, площадь поперечного сечения – ω, а расстояние между сечениями 1-1 и 2-2 буквой L.
Воспользуемся теоремой о количестве движения, согласно которой приращение количества движения системы за некоторый промежуток времени равно сумме проекций импульсов сил на направление движения. Рассмотрим жидкость между сечениями 1-1 и 2-2. В момент закрытия крана количество движения этой жидкости равнялось mv (где m – масса жидкости, равная ρωL, a v – скорость), а через промежуток времени 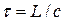 , т. е. когда вся жидкость в трубе остановится и скорость будет равна нулю, количество движения также будет равно нулю. Следовательно, за время
, т. е. когда вся жидкость в трубе остановится и скорость будет равна нулю, количество движения также будет равно нулю. Следовательно, за время 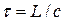 приращение количества движения равно (-ρωLv).
приращение количества движения равно (-ρωLv).
В течение этого же времени, т. е. времени 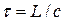 , на жидкость действовали следующие силы, не считая сил трения, которыми пренебрегаем:
, на жидкость действовали следующие силы, не считая сил трения, которыми пренебрегаем:
1) в сечении 1-1 сила p1ω;
2) в сечении 2–2 сила p2ω;
3) сила тяжести жидкости G.
Первые две силы горизонтальны, третья вертикальна. Сумма проекций импульсов этих сил на направление движения, т. е. на горизонтальную ось, равна
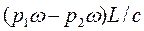
Согласно теореме о количестве движения, получаем
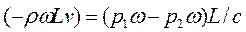
откуда
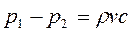

 Обозначая повышение давления
Обозначая повышение давления 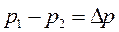 , находим
, находим
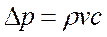 (87)
(87)
Формула (87) называется формулой Н. Е. Жуковского, который первым дал теорию гидравлического удара. Разделив выражение (87) на ρg, получим
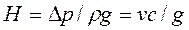 (88)
(88)
Из формулы (88) видно, что при гидравлическом ударе повышение напора в трубопроводе равно  .
.
Численное значение величины с также выведено Н. Е. Жуковским и определяется по следующей формуле:
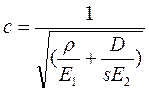 (89)
(89)
где ρ – плотность жидкости;
E1 – модуль упругости жидкости;
E2 – модуль упругости стенок трубы;
D – внутренний диаметр трубы;
s – толщина стенки трубы.
Как сказано выше, гидравлический удар может повредить трубы. Для предохранения труб от разрушения принимаются следующие меры.
1. Из формулы (87) видно, что увеличение давления пропорционально скорости течения v, поэтому в трубопроводах не следует допускать больших скоростей без принятия соответствующих предохранительных мер.
2. Причиной гидравлического удара является быстрое закрытие крана, поэтому следует устраивать краны и задвижки, закрывающиеся медленно; время закрытия τв секундах может быть подсчитано по формуле Н. Е. Жуковского
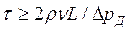 (90)
(90)
где ρ – плотность жидкости, кг/м3; v – скорость течения, м/сек; L -длина трубопровода, м;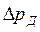 – допускаемое повышение давления, н/м2.
– допускаемое повышение давления, н/м2.
Необходимо отметить на основании формулы (90), что время закрытия τ прямо пропорционально длине трубопровода L, т. е. чем длиннее трубопровод, тем длительнее должно быть закрытие кранов и задвижек.
3. Для уменьшения вредного действия давления при гидравлическом ударе устраивают предохранительные клапаны, которые, открываясь при определенном давлении, предохраняют трубопровод от разрушения.
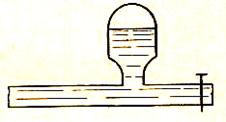
Рис.44.
4. Кроме предохранительных клапанов, для уменьшения давления применяют воздушные колпаки (рис.44). В момент повышения давления жидкость входит в колпаки сжимает находящийся в нем воздух, что уменьшает повышение давления.

ГЛАВА ДЕВЯТАЯ
Дата добавления: 2021-04-18; просмотров: 8; Нарушение авторских прав

§
1. Вытекание жидкости через отверстие втонкой стенке
Рассмотрим случай вытекания жидкости в атмосферу через отверстие площадью ω (рис.45).
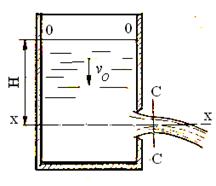
Рис.45.
Струя при вытекании через отверстие постепенно сжимается. Ближайшее к отверстию наименьшее живое сечение С-С, в котором движение можно рассматривать плавноизменяющимся, называется сжатым сечением. Обозначим площадь сжатого сечения С-С буквой ωсж. Отношение
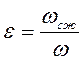 (91)
(91)
называется коэффициентом сжатия.
Так как отдельные струйки в сжатом сечении почти параллельны, то можно считать, что давление в нем равно давлению окружающей среды, т. е. в данном случае барометрическому давлению рб.
Обозначим Н высоту уровня жидкости над центром тяжести отверстия, v -скорость в сжатом сечении. Выберем за ось координат горизонтальную ось X-X, проходящую через центр тяжести отверстия, и напишем уравнение Бернулли для сечения О-О и сжатого сечения С-С:
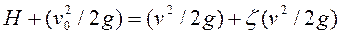 ,
,
где v0 – скорость воды в сосуде.
Пренебрегая величиной (v02/2g) (ввиду ее малости по сравнению с Н), получим
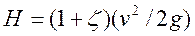 ,
,
откуда скорость вытекания
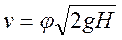 (92)
(92)
где 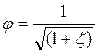 называют коэффициентом скорости. Коэффициент скорости является отношением скоростей реальной и идеальной жидкости при вытекании через отверстия и насадки.
называют коэффициентом скорости. Коэффициент скорости является отношением скоростей реальной и идеальной жидкости при вытекании через отверстия и насадки.
Для вычисления расхода жидкости через отверстие надо скорость умножить на площадь сжатого сечения:

Учитывая, что 
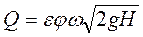 (93)
(93)
Обозначим
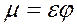 (94)
(94)
Величина μ называется коэффициентом расхода (отношение расхода реальной жидкости через отверстие к расходу идеальной жидкости при вытекании через отверстия и насадки). Выражение (94) является безразмерной формой для уравнения неразрывности потока, а (93) принимает вид
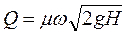 (95)
(95)
Дата добавления: 2021-04-18; просмотров: 13; Нарушение авторских прав
§
На рис.47,а изображен сосуд, имеющий в одной из своих стенок отверстие. Обозначим толщину стенки сосуда L , а диаметр отверстия D. Если L< 3D, то стенку рассматривают как тонкую и отверстие называют отверстием в тонкой стенке. При вытекании жидкости через такое отверстие все потери напора сведутся к местным потерям. При L=3÷5D отверстие рассматривается, как короткая трубка, вставленная в отверстие или насадок (рис.47,б).

а) б)
Рис.47.
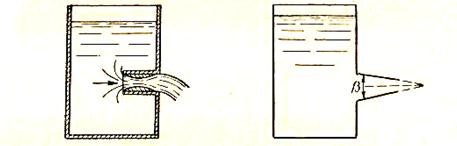
а) б)
Рис.48.
Насадки разделяются на цилиндрические и конические. Цилиндрические насадки могут быть внешние (рис.47,б) и внутренние (рис48,а). Конические насадки бывают конически сходящиеся (рис.48,б) и конически расходящиеся (рис.49 и 50), причем угол β между образующими конуса называется углом конусности. Если в конически расходящейся насадке (β>0,04π) то, как показывают опыты, струя вытекает из отверстия, не касаясь стенок насадки (рис.50).

Рис.49.

Рис.50.
Дата добавления: 2021-04-18; просмотров: 20; Нарушение авторских прав
§
В данном случае движение является неустановившимся. С достаточной степенью точности для практики можно считать, что в каждый данный момент времени скорость вытекания определяется соответствующим этому
моменту напором Н так же, как и при установившемся движении.
Определим время, в течение которого жидкость опустится на 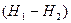 , (рис.51). Возьмем промежуточное положение уровня с напором Н. За время dτ вытечет объем жидкости, равный
, (рис.51). Возьмем промежуточное положение уровня с напором Н. За время dτ вытечет объем жидкости, равный
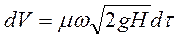 (98)
(98)
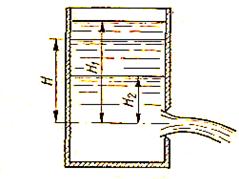
Рис.51
За то же время dτ напор изменится на (-dH).Объем жидкости, вытекшей из сосуда, равен
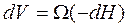 (99)
(99)
где Ω – площадь свободной поверхности в сосуде.
В выражении (99) знак минус учитывает отрицательный характер приращения dHпри понижении уровня. Приравняв (98) и (99), получим

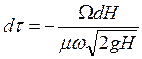
Интегрируя последнее выражение от Н2 до2 Н1 получим:
 (100)
(100)
В случае, когда Ω является переменной величиной, время опорожнения сосуда вычисляется, как
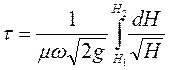 (101)
(101)
Дата добавления: 2021-04-18; просмотров: 6; Нарушение авторских прав
§
Жидкость представляет собой не сплошное непрерывное тело, а тело, состоящее из молекул, расположенных на некотором (весьма небольшом) расстоянии друг от друга. Как видно, жидкость, строго говоря, имеет прерывную структуру. Однако при решении различных гидромеханических задач пренебрегают отмеченным обстоятельством и рассматривают жидкость как сплошную (непрерывную), однородную среду.
Именно такую модель сплошной однородной среды, как правило, и будем иметь в виду далее. Только в некоторых особых случаях нам придется сталкиваться с нарушением сплошности, непрерывности жидкости.
Поясним в общих чертах такие особые случаи применительно к практике гидротехнического строительства (в связи с чем, как пример жидкости, будем иметь в виду воду).
1. Переход воды в твердое или газообразное состояние
Образование в воде кристаллов льда.
Как отмечалось выше, при повышении давления или при снижении температуры в воде могут зарождаться кристаллы льда, причем вместо однородной сплошной среды получаем двухфазную систему (вода плюс лед).
Образование в воде областей (разрывов), заполненных воздухом и парами воды. Кипение и кавитация.
Обычно в воде содержится растворенный воздух. Как
известно из курса физики, при снижении давления р в жидкости или при повышении ее температуры t° такой воздух начинает выделяться из отдельных элементарных объемов воды, причем в воде образуются разрывы (воздушные «пузыри»). В результате сплошность воды нарушается: до тех пор, пока пузыри, воздуха не выйдут из нее через ее свободную поверхность,
будем иметь двухфазную систему (вода плюс воздушные пузыри).
Рассмотрим далее воду, не содержащую растворенного воздуха. Обозначим через рнп давление паров воды, насыщающих то пространство, в котором они находятся. Величину рнп обычно называют «давлением насыщенных паров». Она зависит от температурыпаров.
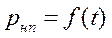
 (102)
(102)
С увеличением температуры давление насыщенных паров жидкости увеличивается.
Предположим, что мы имеем некоторый объем воды,  сплошность которого не нарушена. Обозначим давление в этой воде через P и температуру ее через t.
сплошность которого не нарушена. Обозначим давление в этой воде через P и температуру ее через t.
Представим себе далее, что в силу тех или других причин температура t начинает увеличиваться или давление p – уменьшаться. Очевидно, в связи с этим в некоторый момент времени можем получить соотношение:

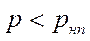 (103)
(103)
Как показывает опыт, при таком соотношении в обычных условиях внутри рассматриваемого объема воды возникают пузырьки, заполненные «насыщенными парами» воды. При этом мы получаем двухфазную систему
(вода плюс пузырьки пара). Чтобы заставить эти пузырьки захлопнуться (закрыться), необходимо добиться соотношения:
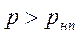 (104)
(104)
т. е. необходимо на достаточную величину или повысить давление р или понизить давление рНП (за счет снижения температуры t). В случае появления в воде пузырьков пара различают два разных явления: кипение и кавитацию.
Кипением жидкости называется явление, когда пузырьки пара, появившиеся в жидкости при соотношении (104), всплывают и выходят из жидкости через ее свободную поверхность.
Кавитацией жидкости называется явление, когда пузырьки пара (или паровоздушные пузырьки), появившиеся при соотношении (104) в движущейся жидкости, не выходят из нее, а захлопываются (закрываются) внутри жидкости.
C тем, чтобы дополнительно пояснить явление кавитации, представим на рис. 54апоток воды, давление вдоль которого (вдоль линии I—I) изменяется, как показано кривой abcdeна рис. 54б. В зоне Апотока, заштрихованной на рисунке, давление 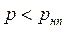 . Линии М1N1и M2N2являются границами этой зоны; во всех точках этих границ
. Линии М1N1и M2N2являются границами этой зоны; во всех точках этих границ 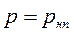 .
.
В элементарных объемах воды, движущихся в направлении стрелок, при пересечении ими границы M1N1 возникнут пузырьки пара; в самой зоне Абудем иметь двухфазную систему; в районе границы M2N2 как показывает опыт, пузырьки пара, попадая в область, где 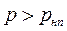 , очень быстро и с большой силой захлопываются, причем за линией M2N2 получаем сплошную среду (такую же, как и перед линией M1N1). Таково явление, называемое кавитацией (от латинского слова «пустота»).
, очень быстро и с большой силой захлопываются, причем за линией M2N2 получаем сплошную среду (такую же, как и перед линией M1N1). Таково явление, называемое кавитацией (от латинского слова «пустота»).
Упомянутое захлопывание пузырьков пара в районе границы M2N2 сопровождается сильными ударами, которые иногда способствуют постепенному разрушению поверхности твердых стенок, ограничивающих поток. Такое разрушение твердых стенок называется кавитационной эрозией.
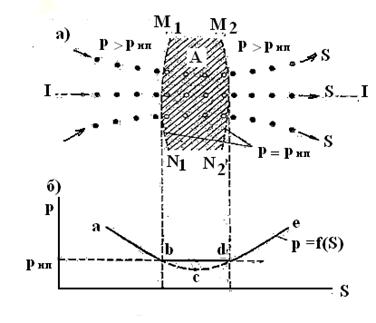
Рис.54.
Существенно подчеркнуть, что появление в воде пузырьков пара (разрывов) в районе зоны А (рис. 54а) препятствует снижению давления в этой зоне до величины, меньшей рнп. Вследствие появления пузырьков пара вместо кривой abсde (рис.54б) получаем кривую abde, показанную сплошной линией (на участке bd — горизонтальной). Следует считать, что практически давление p в воде, в силу сказанного, не может быть меньше величины 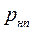 .
.
Присоединение к движущейся жидкости газообразных и твердых тел.
1. Аэрация потока. Если к потоку воды, движущейся с большими скоростями, имеется доступ наружного воздуха, то поток может насыщаться проникающими в него снаружи пузырьками воздуха. В результате получается смесь воды и пузырьков воздуха (двухфазная система). Такое явление называется аэрацией потока.

2. Захват потоком наносов. Если водный поток имеет размываемое русло (например, русло, образованное мелким песком), то, как показывает опыт, при достаточно больших скоростях движения воды поток начинает насыщаться песчинками, которые движутся вместе с водой во взвешенном состоянии. Здесь также получаем двухфазную систему. Заметим, что обычно, помимо взвешенных песчинок, имеются еще песчинки, перемещающиеся непосредственно по дну русла.
Дата добавления: 2021-04-18; просмотров: 50; Нарушение авторских прав

Удельная энергия потока и удельная энергия сечения.



Удельная энергия потока и удельная энергия сечения. Описан анализ движения открытого потока с энергетической точки зрения. Механическая энергия массы жидкости, протекающей в единицу времени с выбранным живым участком потока, которая называется единицей веса и определяется для любой горизонтальной плоскости, обозначается через Е, которая называется удельной энергией потока. При анализе изменений е вдоль течения последние должны быть рассчитаны для всех живых участков, относящихся к одной горизонтальной поверхности. Учитывая сказанное ранее, для любой точки в Живом сечении потока, при плавно меняющемся движении, можно написать: Е = 2 р /р§ ос2 /2§ = А ч ос2 / 2 | р(15.13) п средства избыточного давления. Ниже по течению удельная энергия потока установившегося движения E всегда должна уменьшаться Cs1E [c11 C0).Это связано с тем, что само движение происходит за счет потребления этой энергии. Нарисуйте плоскость сравнения 0-0 в нижней части указанного сечения (рис.15.2, 0 ’to0′), а не произвольно. 312.
Представим, что открытый поток движется по дну произвольного очертания под действием силы тяжести от точкиА до точки В. При этом происходит преобразование потенциальной энергии в кинетическую.
Людмила Фирмаль
- Удельная энергия определенного живого сечения, определенная для горизонтальной плоскости, проходящей через самую нижнюю точку этого сечения, называется удельной энергией сечения и обозначается символом Е. Е = К = ч (15.14) 2Б. Понятие удельной энергии поперечного сечения полезно для анализа стационарного движения жидкости в открытых каналах. Также отметим, что значение е вычисляется для каждого живого участка потока, относительно горизонтальной плоскости сравнения.
- Из (15.13) и (15.14)、 И-И-и-И. 4Е О2 Тогда считайте это—4、 41, co2C2 I. Мы получаем (15.15) (15.16) 4Э 4Э. 。О, нет. {Я ■С 41, 41so2, Х2 Или О 4Е. нет. Л <* 1с1 ко _. Л * О. 41-е? С? I-V I / H KКак видно из уравнения (15.16), можно видеть, что K = Ko является равномерным движением ЭЭ/ (==0 и<1e / < ^ ^ 0 является неравномерным движением в зависимости от значения отношения ko / k. Смысл последнего положения заключается в том, что при равномерном движении работа силы тяжести полностью расходуется на преодоление силы сопротивления, а удельная энергия поперечного сечения не изменяется.
Напомним, что механическая энергия жидкости, протекающей в единицу времени через выбранное сечение потока, отнесённая к весу и определяемая относительно произвольной горизонтальной плоскости, называется удельной энергией потока Е.
Людмила Фирмаль
- В случае КЖ средний расход меньше, чем в случае равномерного движения, гидравлическое сопротивление уменьшается, и часть работы силы тяжести постепенно накапливает определенную энергию в нижнем сечении. При K K0 картина меняется на обратную. То есть на преодоление сопротивления затрачивается больше энергии, чем может дать работа гравитации, а требуемая дополнительная энергия заимствуется из удельной энергии нижележащего участка, то есть т. е. / < 11 <0. В заключение следует отметить, что при 1 = 0 или r <0 равенство (15.15) подразумевает только отрицательные значения производной.
Смотрите также:
Решение задач по гидравлике
Возможно эти страницы вам будут полезны:
- Дифференциальное уравнение установившегося плавно изменяющегося движения жидкости.
- Основные виды установившегося движения жидкости в призматическом открытом русле.
- Спокойные и бурные потоки. критическая глубина.
- Критический уклон.








