Теория диффузии в газах на основе уравнения больцмана
В кинетике Больцмана смеси газов каждый газ имеет свою собственную функцию распределения , где t – момент времени, x – положение, а c – скорость молекулы i- го компонента смеси. Каждый компонент имеет свою среднюю скорость . Если скорости не совпадают, то существует диффузия .
жя(Икс,c,т){ Displaystyle f_ {я} (х, с, т)}Cя(Икс,т)знак равно1пя∫ccж(Икс,c,т)dc{ displaystyle C_ {i} (x, t) = { frac {1} {n_ {i}}} int _ {c} cf (x, c, t) , dc}Cя(Икс,т){ Displaystyle C_ {я} (х, т)}
В приближении Чепмена – Энскога все функции распределения выражаются через плотности сохраняющихся величин:
- индивидуальные концентрации частиц (частиц на объем),пя(Икс,т)знак равно∫cжя(Икс,c,т)dc{ Displaystyle п_ {я} (х, т) = int _ {с} f_ {я} (х, с, т) , dc}
- плотность количества движения ( m i – масса i- й частицы),∑ямяпяCя(Икс,т){ Displaystyle сумма _ {я} м_ {я} п_ {я} С_ {я} (х, т)}
- плотность кинетической энергии
- ∑я(пямяCя2(Икс,т)2 ∫cмя(cя-Cя(Икс,т))22жя(Икс,c,т)dc).{ displaystyle sum _ {i} left (n_ {i} { frac {m_ {i} C_ {i} ^ {2} (x, t)} {2}} int _ {c} { frac {m_ {i} (c_ {i} -C_ {i} (x, t)) ^ {2}} {2}} f_ {i} (x, c, t) , dc right). }
Кинетическая температура T и давление P определяются в трехмерном пространстве как
- 32kBТзнак равно1п∫cмя(cя-Cя(Икс,т))22жя(Икс,c,т)dc;пзнак равноkBпТ,{ displaystyle { frac {3} {2}} k _ { rm {B}} T = { frac {1} {n}} int _ {c} { frac {m_ {i} (c_ { i} -C_ {i} (x, t)) ^ {2}} {2}} f_ {i} (x, c, t) , dc; quad P = k _ { rm {B}} nT ,}
где – полная плотность.
пзнак равно∑япя{ Displaystyle п = сумма _ {я} п_ {я}}Для двух газов разность скоростей определяется выражением:
C1-C2{ displaystyle C_ {1} -C_ {2}}
- C1-C2знак равно-п2п1п2D12{∇(п1п) п1п2(м2-м1)пп(м1п1 м2п2)∇п-м1п1м2п2п(м1п1 м2п2)(F1-F2) kТ1Т∇Т},{ displaystyle C_ {1} -C_ {2} = – { frac {n ^ {2}} {n_ {1} n_ {2}}} D_ {12} left { nabla left ({ frac {n_ {1}} {n}} right) { frac {n_ {1} n_ {2} (m_ {2} -m_ {1})} {Pn (m_ {1} n_ {1} m_ {2} n_ {2})}} nabla P – { frac {m_ {1} n_ {1} m_ {2} n_ {2}} {P (m_ {1} n_ {1} m_ {2} n_ {2})}} (F_ {1} -F_ {2}) k_ {T} { frac {1} {T}} nabla T right },}
где – сила, приложенная к молекулам i- го компонента, – коэффициент термодиффузии.
Fя{ displaystyle F_ {i}}kТ{ displaystyle k_ {T}}
Коэффициент D 12 положительный. Это коэффициент диффузии. Четыре члена в формуле для C 1 – C 2 описывают четыре основных эффекта при диффузии газов:
- ∇(п1п){ displaystyle nabla , left ({ frac {n_ {1}} {n}} right)}описывает поток первого компонента из областей с высоким отношением n 1 / n к областям с меньшими значениями этого отношения (и аналогично поток второго компонента от высокого n 2 / n к низкому n 2 / n, потому что n 2 / n = 1 – n 1 / n );
- п1п2(м2-м1)п(м1п1 м2п2)∇п{ displaystyle { frac {n_ {1} n_ {2} (m_ {2} -m_ {1})} {n (m_ {1} n_ {1} m_ {2} n_ {2})}} nabla P}описывает поток более тяжелых молекул в области с более высоким давлением и более легких молекул в области с более низким давлением, это бародиффузия ;
- м1п1м2п2п(м1п1 м2п2)(F1-F2){ displaystyle { frac {m_ {1} n_ {1} m_ {2} n_ {2}} {P (m_ {1} n_ {1} m_ {2} n_ {2})}} (F_ { 1} -F_ {2})}описывает диффузию, вызванную различием сил, приложенных к молекулам разных типов. Например, в гравитационном поле Земли более тяжелые молекулы должны опускаться, или в электрическом поле заряженные молекулы должны двигаться, пока этот эффект не уравновесится суммой других членов. Этот эффект не следует путать с бародиффузией, вызванной градиентом давления.
- kТ1Т∇Т{ displaystyle k_ {T} { frac {1} {T}} nabla T}описывает термодиффузию , диффузионный поток, вызванный температурным градиентом.
Все эти эффекты называются диффузией, потому что они описывают разницу между скоростями различных компонентов в смеси. Следовательно, эти эффекты не могут быть описаны как массовый перенос и отличаются от адвекции или конвекции.
В первом приближении
Число определяется квадратурами (формулы (3.7), (3.9), гл.10 классической книги Чепмена и Каулинга)
А1(ν){ displaystyle A_ {1} ({ nu})}
Мы видим, что зависимость от T для жестких сфер такая же, как и для простой теории длины свободного пробега, но для степенных законов отталкивания показатель степени другой. Зависимость от общей концентрации n для данной температуры всегда имеет один и тот же характер – 1 / n .
В приложениях к газовой динамике диффузионный поток и объемный поток должны быть объединены в одну систему уравнений переноса. Объемный поток описывает массообмен. Его скорость V – это средняя массовая скорость. Он определяется через плотность импульса и массовые концентрации:
- Vзнак равно∑яρяCяρ.{ displaystyle V = { frac { sum _ {i} rho _ {i} C_ {i}} { rho}} ,.}
где – массовая концентрация i- го компонента , – массовая плотность.
ρязнак равномяпя{ Displaystyle rho _ {я} = м_ {я} п_ {я}}ρзнак равно∑яρя{ Displaystyle rho = сумма _ {я} rho _ {я}}По определению, скорость диффузии я го компонента , . Массоперенос i- го компонента описывается уравнением неразрывностиvязнак равноCя-V{ displaystyle v_ {i} = C_ {i} -V}∑яρяvязнак равно0{ Displaystyle сумма _ {я} ро _ {я} v_ {я} = 0}
- ∂ρя∂т ∇(ρяV) ∇(ρяvя)знак равноWя,{ Displaystyle { гидроразрыва { partial rho _ {i}} { partial t}} nabla ( rho _ {i} V) nabla ( rho _ {i} v_ {i}) = W_ {i} ,,}
где это чистая дебит массы в химических реакциях, .
Wя{ displaystyle W_ {i}}∑яWязнак равно0{ Displaystyle сумма _ {я} W_ {я} = 0}В этих уравнениях термин описывает перенос i- го компонента, а термин представляет диффузию этого компонента.
∇(ρяV){ Displaystyle набла ( ро _ {я} V)}∇(ρяvя){ Displaystyle набла ( ро _ {я} v_ {я})}
В 1948 году Венделл Х. Ферри предложил использовать форму скоростей диффузии, найденную в кинетической теории, в качестве основы для нового феноменологического подхода к диффузии в газах. Этот подход был разработан Ф.А. Уильямсом и С.Х. Ламом. Для скоростей диффузии в многокомпонентных газах ( N компонентов) они использовали
- vязнак равно-(∑jзнак равно1NDяjdj Dя(Т)∇(перТ));{ displaystyle v_ {i} = – left ( sum _ {j = 1} ^ {N} D_ {ij} mathbf {d} _ {j} D_ {i} ^ {(T)} , nabla ( ln T) right) ,;}
- djзнак равно∇Иксj (Иксj-Yj)∇(перп) граммj;{ Displaystyle mathbf {d} _ {j} = nabla X_ {j} (X_ {j} -Y_ {j}) , nabla ( ln P) mathbf {g} _ {j} ,;}
- граммjзнак равноρп(Yj∑kзнак равно1NYk(жk-жj)).{ displaystyle mathbf {g} _ {j} = { frac { rho} {P}} left (Y_ {j} sum _ {k = 1} ^ {N} Y_ {k} (f_ { k} -f_ {j}) right) ,.}
Здесь – матрица коэффициентов диффузии, – коэффициент термодиффузии, – массовая сила на единицу массы, действующая на i- й компонент , – доля парциального давления i- го компонента (и – парциальное давление), – массовая доля из я видов м, иDяj{ displaystyle D_ {ij}}Dя(Т){ displaystyle D_ {i} ^ {(T)}}жя{ displaystyle f_ {i}}Иксязнак равнопя/п{ Displaystyle X_ {i} = P_ {i} / P}пя{ displaystyle P_ {i}}Yязнак равноρя/ρ{ Displaystyle Y_ {я} = rho _ {i} / rho}∑яИксязнак равно∑яYязнак равно1.{ displaystyle sum _ {i} X_ {i} = sum _ {i} Y_ {i} = 1.}

Поскольку носители генерируются (зеленый: электроны и фиолетовый: дырки) из-за света, сияющего в центре собственного полупроводника, они рассеиваются к двум концам. Электроны имеют более высокую константу диффузии, чем дырки, что приводит к меньшему количеству избыточных электронов в центре по сравнению с дырками.
Измерений и дозиметрии

Количественной характеристикой активности радиоактивного нуклида в системе единиц СИ является активность нуклида, в котором за 1 с происходит один акт распада. Эта единица называется беккерель, условное обозначение – Бк, размерность – с-1. Поскольку беккерель – очень малая единица, то широко используется внесистемная единица – кюри, условное обозначение Ки. 1 Ки = 3,700∙1010 Бк.
Отношение активности радионуклида в источнике к массе или объёму этого источника называется удельной активностью источника и обозначается соответственно Am или Av для объёмных источников, As – для поверхностных источников и AL – для линейных источников.
Массу m (в граммах) радиоактивного нуклида активностью А (в беккерелях) без учёта массы неактивного носителя можно рассчитать по формуле [3]:
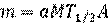 , (1.12)
, (1.12)
где M – атомная масса радионуклида;
Т1/2 – период полураспада;
а – константа, зависящая от единиц, в которых выражается Т1/2 (см. табл. 1.2).
И наоборот, активность А (в беккерелях) радионуклида массой m (в граммах) без учёта массы неактивного носителя рассчитывается по формуле
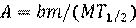 , (1.13)
, (1.13)
где b – константа, зависящая от единиц, в которых выражается Т1/2 (см. табл. 1.2).
Исчерпывающая информация о поле частиц задаётся распределением частиц во времени, в пространстве и по энергии. Иными словами, для полного представления о поле излучения необходимо указать, сколько частиц, с какой энергией и в каком направлении приходит в любую точку области пространства в каждый момент времени.
Таблица 1.2
Константы для формул (1.12), (1.13)
| Константа | Т1/2 выражена в | ||||
| секундах | Минутах | Часах | сутках | годах | |
| a | 2,4∙10-24 | 1,44∙10-22 | 8,62∙10-21 | 2,07∙10-19 | 7,56∙10-17 |
| B | 4,17∙1023 | 6,94∙1021 | 1,16∙1020 | 4,83∙1018 | 1,32∙1016 |
Количественными характеристиками излучений являются флюенс, поток частиц, плотность потока частиц, ток частиц, плотность тока частиц и интенсивность излучения.
Согласно определению Международной электротехнической комиссии (МЭК) флюенс – есть частное от деления числа частиц dN, входящих в элементарную сферу с площадью центрального сечения dS, на величину dS:
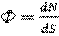 . (1.14)
. (1.14)
Здесь подразумевается, что направления движения частиц, попадающих в элементарную сферу, могут быть различными, а значит, положение центрального сечения этой сферы не является фиксированным, поскольку для каждого направления движения частицы будет своё положение центрального сечения этой сферы, перпендикулярное направлению скорости этой частицы. Лишь для мононаправленного потока частиц положение сечения элементарной сферы окажется фиксированным и перпендикулярным направлению вектора скорости движения частиц.
Единицей измерения флюенса в системе СИ является м-2 или см-2.
Поток частиц F – есть отношение числа ионизирующих частиц dN, проходящих через заданную поверхность за интервал времени dt, к этому интервалу:
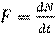 . (1.15)
. (1.15)
Единицей измерения потока излучения является с-1.
Плотность потока частиц φ(r) в точке r есть число частиц, проникающих за единицу времени в объём элементарной сферы, расположенной с центром в точке r, отнесённое к площади проекции dS этой сферы:
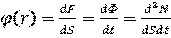 . (1.16)
. (1.16)
Из математической записи плотности потока следует её тесная связь с потоком и флюенсом. Плотность потока представляет собой производную от потока по площади проекции элементарной сферы, для которой он определён, или же производную от флюенса через эту сферу по времени.
Размерность единицы плотности потока частиц в системе СИ: с-1∙м-2.
Учитывая, что на практике часто необходимо определять количество частиц, проходящих через площадку, произвольным образом ориентированную относительно направления распространения частиц (например, через площадку, расположенную на границе объёмного источника или на поверхности облучаемого объекта), вместо потоковых характеристик более удобно использовать токовые характеристики.
Плотность скалярного тока частиц Jk(r,Ω)черезэлементарную площадку dS, расположенную перпендикулярно вектору k, не совпадающему с направлением распространения частиц, определяемым телесным углом Ω,равна числу частиц, пересекающих эту площадку за единицу времени.
На рисунке 1.3 поясняется различие между этими определениями.
Очевидно, что плотность скалярного тока частиц представляет собой проекцию вектора потока частиц в данной точке на направление вектора k. Понятно, что измеряется она в тех же единицах, что и плотность потока.
Рис. 1.3. К определению понятий плотности потока частиц (а)
и плотности скалярного тока частиц (б)
Поток частиц ФS и скалярный ток частиц JS за время Т через площадку S определяется интегрированием соответственно плотности потока и плотности скалярного тока частиц через данную площадку по поверхности данной площадки и по времени:
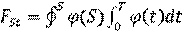 ; (1.17)
; (1.17)
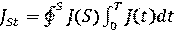 . (1.18)
. (1.18)
Если нас интересует не поток частиц, а поток энергии этих частиц, то она определяется пространственным и энергетически-угловым распределением плотности потока энергии частиц: I(r, E, Ω) = Eφ(r,Ω). Она характеризуется интенсивностью излучения. Для расчёта интенсивности излучения необходимо знать не только его плотность, но и энергетический спектр φ(E):
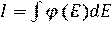 . (1.19)
. (1.19)
Для изотропного равномерного поля излучения интенсивность излучения I(r) – это количество энергии, переносимое за единицу времени через единичную площадку, расположенную перпендикулярно к скорости частиц. В системе СИ единицей измерения интенсивности излучения является Дж/(м2∙с). Однако при расчётах и измерениях радиационных излучений чаще пользуются внесистемной единицей МэВ/(м2∙с) или эВ/(см2∙с).
Интенсивность моноэнергетического изотропного излучения равна
I= φЕ . (1.20)
По пространственно-временной энергетически-угловой плотности потока частиц φ(r, t, E,Ω) можно рассчитать для любой точки пространства и любого момента времени любую дозиметрическую характеристику поля излучения. Эти характеристики принято делить на два класса: базисные величины, определяемые в исходном поле, свободном от каких-либо возмущений, и фантомные величины, учитывающие возмущения, вносимые в исходное поле фантомом, имитирующем тело человека (или другие объекты).
Базисные величины относятся к элементарному объёму в точке определения данной дозиметрической величины и определяются только характеристиками исходного радиационного поля. Фантомные величины относятся к заданной точке детектирования внутри фантома или на его поверхности и определяются не только характеристиками исходного поля, но и всеми параметрами фантома (геометрия, размеры, состав).
Основной физической величиной, определяющей степень радиационного воздействия, является поглощённая доза ионизирующего излучения.
Поглощённая доза ионизирующего излучения D есть отношение средней энергии dW, переданной ионизирующим излучением веществу в элементарном объёме к массе dm этого вещества в данном объёме:
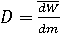 . (1.21)
. (1.21)
Единицей поглощённой дозы в системе СИ является грей (Гр) равный поглощённой дозе веществом массой в 1 кг, которому передана энергия ионизирующего излучения, равная 1 Дж, т.е. 1 Гр = 1 Дж/кг. Внесистемной единицей поглощённой дозы является рад равный поглощённой дозе веществом массой в 1 г, которому передана энергия ионизирующего излучения, равная 100 эрг. 1 рад = 100 эрг/г = 0,01 Гр. Здесь следует иметь в виду, что под переданной энергией понимается разность суммарной кинетической энергии ионизирующего излучения, входящего в данный объём потока и суммарной кинетической энергии выходящего из данного объёма потока ионизирующего излучения. Если в рассматриваемом объёме в процессе поглощения ионизирующего излучения происходили превращения ядер или элементарных частиц, то к указанной выше разности следует прибавить разность между суммой всех выделенных энергий и суммой всех затраченных энергий, сопровождающих эти превращения.
Производная поглощённой дозы по времени называется мощностью поглощённой дозы. Её размерность: Гр/с или Вт/кг. Мощность поглощённой дозы в 1 Гр/с равна поглощённой дозе стационарного излучения в 1 Гр, полученной за 1 с.
Для фотонного (рентгеновского и гамма-излучения) часто используют другую характеристику – экспозиционную дозу излучения. Она представляет собой отношение суммарного заряда dQ всех ионов одного знака, созданных в сухом воздухе, когда все электроны и позитроны, освобождённые фотонами в элементарном объёме воздуха с массой dm, полностью потеряли свою кинетическую энергию в этом объёме воздуха, к массе воздуха в данном объёме dm [3]:
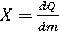 . (1.22)
. (1.22)
Единицей экспозиционной дозы в системе единиц СИ является кулон/кг (Кл/кг). Следовательно, эта единица соответствует такой экспозиционной дозе, при которой все электроны и позитроны, освобождённые фотонами в воздухе массой в 1 кг, образуют в этом объёме воздуха ионы, несущие электрический заряд в 1 Кл каждого знака. Учитывая, что заряд иона равен 1,602∙10-19 Кл, экспозиционной дозе в 1 Кл/кг будет соответствовать образование 1/1,602∙10-19 = 6,24∙1018 пар ионов. Если принять среднюю энергию образования одной пары ионов для воздуха равной 33,85 эВ (учитывающую молекулярный состав воздуха), то можно получить энергетический эквивалент единицы экспозиционной дозы, который равен 2,11 ∙1014 МэВ или 33,85 Дж. Это означает, что данное количество энергии будет затрачено на ионизацию 1 кг сухого воздуха, чтобы получить в нём 6,24∙1018 пар ионов с суммарным зарядом каждого знака в 1 Кл.
Внесистемной единицей экспозиционной дозы является рентген – Р.
Рентген соответствует экспозиционной дозе фотонного излучения, при прохождении которого через 0,001293 г воздуха создаются ионы, несущие 1 Кл заряда каждого знака. (0,001293 г – это масса 1 см3 сухого воздуха при температуре 00 С и давлении 103,3 кПа). 1 Р = 2,58∙10-4 Кл/кг. Энергетический эквивалент 1 рентгена составляет 7,05 ∙104 МэВ или 1,13∙10-8 Джна 1 см3 воздуха. Экспозиционная доза не учитывает ионизацию, обусловленную тормозным излучением электронов и позитронов, поскольку для воздуха этой величиной можно пренебречь ввиду её малости.
В процессе перехода на систему единиц СИ экспозиционная доза подлежит изъятию из обращения. Это связано с тем, что она была введена только для фотонного излучения с энергией до 3 МэВ, в то время как на практике чаще встречаются смешанные излучения. Кроме того, значения экспозиционной дозы в рентгенах и поглощённой дозы в воздухе в радах различаются лишь в 1,14 раза. Таким образом, сосуществование этих двух характеристик излучения теряет смысл. Здесь она приведена лишь постольку, поскольку в литературе прежних лет издания она использовалась достаточно широко.
Для оценки биологического эффекта воздействия ионизирующего излучения потребовалось введение специальной характеристики количества излучения – эквивалентной дозы или эквивалента поглощённой дозы в органе или биологической ткани. Она получена из поглощённой дозы, усреднённой по объёму ткани или органа. Эта характеристика рекомендована Международной комиссией по радиационной защите (МКРЗ): Рекомендации МКРЗ, 1990 г. [4]. Эквивалентная доза HTR в ткани или органе Т, созданная излучением R, определяется выражением
HTR = wRDTR , (1.23)
где DTR – средняя поглощённая доза в ткани или органе Т;
wR – весовой множитель для данного вида и энергии излучения.
Т.к. весовой множитель wRявляется безразмерной величиной, то эквивалентная доза имеет ту же размерность, что и поглощённая доза: Дж/кг, но имеет другое название – зиверт (Зв). Если поле излучения содержит несколько видов излучения различных энергий, то эквивалентная доза такого излучения должна определяться как сумма эквивалентных доз от каждой составляющей этого сложного излучения:
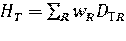 , (1.24)
, (1.24)
где DTR – средняя поглощённая доза от излучения R в ткани или органе Т.
На разные органы и ткани ионизирующие излучения влияют неодинаково, т.е. допустимые дозы излучения для разных органов и тканей различны. Эти различия учитываются тканевым весовым множителем wT . Численные значения этих множителей выбраны такими, чтобы их сумма для всех органов и тканей человеческого тела давала единицу. В этом случае равномерное облучение всего тела по величине соответствующее какой-то эквивалентной дозе для всего тела будет давать ту же эквивалентную дозу и для каждого органа и ткани в отдельности. Числовые значения тканевых весовых множителей для человека представлены в таблице 1.3.
Эффективная доза Е для всего тела представляет собой сумму взвешенных эквивалентных доз во всех тканях и органах:
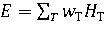 . (1.25)
. (1.25)
Подставляя сюда НТ из (1.20), получаем
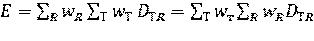 . (1.26)
. (1.26)
Таблица 1.3
Тканевые весовые множитель для тела человека
| Ткань или орган | Тканевой весовой множитель wT | Ткань или орган | Тканевой весовой множитель wT | |
| Половые железы Красный костный мозг Толстый кишечник Лёгкие Желудок Мочевой пузырь | 0,20 0,12 0,12 0,12 0,12 0,05 | Молочные железы Печень Пищевод Щитовидная железа Кожа Поверхность кости Остальные органы | 0,05 0,05 0,05 0,05 0,01 0,01 0,05 |
Единицей мощности эквивалентной дозы является 1 зиверт в секунду (1 Зв/с). Внесистемной единицей эквивалентной дозы является бэр. 1 бэр = 0,01 Дж/кг = 0,01 Зв. Внесистемной единицей мощности эквивалентной дозы является 1 бэр/с.
Для оценки воздействия на вещество косвенно ионизирующих излучений (гамма- и нейтронного) используют понятие керма (от англ. kerma – kinetik energy released in material). Керма (К) представляет собой отношение суммы первоначальных кинетических энергий dWk всех заряженных ионизирующих частиц, образованных под действием косвенно ионизирующего излучения в элементарном объёме вещества, к массе dm вещества в этом объёме:
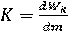 . (1.27)
. (1.27)
Единица кермы – грей совпадает с единицей поглощённой дозы. Внесистемной единицей кермы является рад.
Для фотонного излучения радиоизотопных источников (с энергией Е0 < 3 МэВ) значение кермы в воздухе может превышать значение поглощённой дозы в воздухе не более, чем на 1 %. Следовательно для этих условий их можно считать равными.
Керма нейтронного излучения совпадает с поглощённой дозой от вторичных заряженных частиц в условиях их равновесия, которые соблюдаются в биологической защите, благодаря её большой толщине и массе. Для тонких поверхностных слоёв биологической ткани и одежды эти характеристики существенно различаются.
Date: 2021-06-08; view: 771; Нарушение авторских прав
§

Источником ионизирующего излучения называют объект, содержащий радиоактивный материал, или техническое устройство, испускающее или способное (при определенных условиях) испускать ионизирующее излучение.
Современные ядерно-технические установки обычно представляют собой сложные источники излучений. Например, источниками излучений действующего ядерного реактора, кроме активной зоны, являются система охлаждения, конструкционные материалы, оборудование и др. Поле излучения таких реальных сложных источников обычно представляется как суперпозиция полей излучения отдельных, более элементарных источников.
Любой источник излучения характеризуется: видом излучении; геометрией источника (формой и размерами); мощностью и её распределением для протяжённых источников; энергетическим спектром; временным распределением излучения; угловым распределением излучения.
Геометрически источники могут быть точечными и протяжёнными. Протяжённыеисточники могут быть линейными, поверхностными или объёмными.
Физически точечным можносчитать такой источник, максимальные размеры которого много меньше расстояния до точки детектирования и длины свободного пробега частиц в материале источника (т.е. ослаблением излучения в самом источнике можно пренебречь) [5].
Поперечные размеры линейных источников должны быть много меньше расстояния до детектора и длины свободного пробега частиц в материале источника [5].
Поверхностные источники имеют толщину много меньшую, чем расстояние до точки детектирования и длина свободного пробега частиц в материале источника [5].
В объёмном источнике излучатели распределены в трёхмерном пространстве и размеры источника больше длины свободного пробега частиц в его материале.
Энергетический спектр излучения источников может быть моноэнергетическим, дискретным или непрерывным.
Моноэнергетическим является, например, гамма-излучение ряда нуклидов, испускающих фотоны только одной энергии, таких как 54Mn, 137Cs, 203Hg, аннигиляционное излучение (энергия излучения определяется массой аннигилирующих частиц) и т.д.
Дискретный спектр имеют альфа-частицы и фотоны большей части радиоактивных нуклидов, излучающих альфа-частицы и электромагнитные кванты.
Непрерывный энергетический спектр характерен для бета-излучения нуклидов, тормозного гамма-излучения (возникающего при бомбардировке вещества потоками электронов и других заряженных частиц), нейтронного излучения при реакциях деления и при реакциях (α, n).
По временному распределению источники разделяют на импульсные, стабильные и нестабильные.
Импульсные источники испускают излучение в течение одного или последовательности интервалов времени, каждый из которых существенно меньше общего времени наблюдения.
Стабильные источники испускают ионизирующие частицы, число которых в единицу времени остаётся стабильным (в определённых пределах) в течение времени наблюдения. У нестабильных источников это условие не соблюдается.
По угловому распределению источники излучения можно разделить на изотропные, косинусоидальные пропорциональные cos θ0, косинусоидальные пропорциональные cosпθ0 и мононаправленное [5]. Диаграммы направленностей этих видов излучений представлены на рисунке 2.1.
РРррр
Угловая функция излучения для этих случаев имеет вид [5]:
– изотропное: 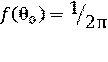 ; (2.1)
; (2.1)
– косинусоидальное пропорциональное cos θ0 :
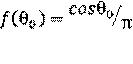 ; (2.2)
; (2.2)
– косинусоидальное пропорциональное cosnθ0 :
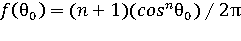 (2.3)
(2.3)
– мононаправленное: 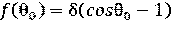 . (2.4)
. (2.4)
Функция f(θ0) в данных распределениях нормирована таким образом, чтобы в единицу времени в полупространство в телесный угол 2π стерадиан точечным источником (или линейным, поверхностным или объёмным) соответственно с единицы длины, площади или объёма испускается одна частица, т.е.
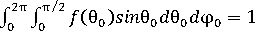 . (2.5)
. (2.5)
Если функцию f(θ0) нормировать так, чтобы излучение испускалось в телесный угол 4π стерадиан, то значения f(θ0) будут в два раза меньше, чем полученные по формулам (2.1 – 2.4).
Распределение (2.3) является наиболее общим. При n = 0 оно преобразуется в (2.1), при n = 1 – в (2.2), а при произвольном n – в распределение (2.4).
Наиболее простым является описание точечного моноэнергетического источника единичной мощности, помещённого в точку с координатами r0. Оно описывается выражением [5]:
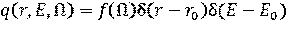 , (2.6)
, (2.6)
где f(Ω) описывает угловое распределение источника излучения;
Е0 – энергия частиц источника;
δ(r – r0) – дельта функция, определяющая зависимость от расстояния до источника;
δ(E – E0) – дельта функция, определяющая зависимость энергии от координат точки детектирования.
Поле точечного изотропного источника в вакууме изменяется обратно пропорционально квадрату расстояния от источника до детектора.
Излучение плоского моноэнергетического источника с энергией частиц Е0 , плоскость которого перпендикулярна некоторому единичному вектору kи проходит через точку r0 , а излучатели распределены равномерно по всей поверхности источника с угловым распределением излучения, задаваемым функцией f(Ω), описывается выражением
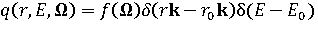 . (2.7)
. (2.7)
Излучение плоских источников нормировано на одну частицу, испускаемую в единицу времени с единичной поверхности источника в телесный угол 2π стерадиан в направлении детектора.
Мононаправленными часто считают точечные изотропные источники, расположенные на значительном расстоянии от облучаемого объекта.
Date: 2021-06-08; view: 1619; Нарушение авторских прав
§

Все ядерные реакции, в результате которых образуются дочерние ядра в возбуждённом состоянии, сопровождаются испусканием гамма-квантов строго определённых энергий. Поэтому все радиоизотопные источники гамма-излучения имеют дискретный энергетический спектр. Непрерывный энергетический спектр характерен лишь для тормозного фотонного излучения (возникающего при бомбардировке вещества потоками высокоэнергичных электронов и других заряженных частиц). Кроме того, во многих практических задачах, когда источник излучения включает в себя множество различных нуклидов, каждый из которых имеет дискретный спектр излучения, в результате их наложения реальный спектр излучения получается практически непрерывным. Примером может служить гамма-излучение реакции деления тяжёлых ядер при бомбардировке их нейтронами, поскольку она может идти по множеству различных путей, результатом которых является образование различных промежуточных и конечных нуклидов и наложение множества дискретных спектров гамма-излучения от этих реакций и даёт в результате практически непрерывный спектр.
Наиболее мощными источниками гамма-излучения (исключая ядерный взрыв) являются ядерные реакторы. При работе ядерного реактора происходит интенсивная бомбардировка нейтронами не только ядерного топлива, но и оболочек ТВЭЛов, вещества замедлителя нейтронов, теплоносителя, конструктивных элементов реактора, биологической защиты и т.п., в результате чего образуется множество различных радиоактивных изотопов [5-7]. Поэтому возникает проблема захоронения не только отработанного ядерного топлива, но и многочисленных технологических радиоактивных отходов (ТРО). По длительности периода полураспада их разделяют на короткоживущие (с периодом полураспада до 15 суток) и долгоживущие (с периодом полураспада от десятков суток до миллионов лет).
Гамма-спектры основных короткоживущих радионуклидов в ТРО, образующихся при работе ядерных реакторов, представлены в таблице 2.1 [3,5-7].
Таблица 2.1
Спектры гамма-излучения некоторых короткоживущих изотопов
| Нуклиды | Период полураспада | Энергия при гамма-распаде, МэВ (выход) |
| I-131 | 8,04 сут. | 0,361 (0,811) |
| I-132 | 2,3 час. | 0,523 (0,161); 0,630 (0,137); 0,668 (0,987); 0,773 (0,762); 0,954 (0,181) |
| I-133 | 20,8 час. | 0,530 (0,863) |
| I-134 | 52,6 мин. | 0,595 (0,114); 0,622 (1,106); 0,847 (0,954); 0,884 (0,652); 1,073 (0,153) |
| I-135 | 6,6 час. | 1,131 (0,225); 1,260 (0,286) |
| Br-82 | 35,3 час. | 0,544 (0,706); 0,619 (0,431); 0,698 (0,282); 0,776 (0,833); 0,828 (0,242); 1,044 (0,273); 1,318 (0,269); 1,475 (0,166) |
| Na-24 | 15 час. | 1,369 (0,99999); 2,754 (0,9986) |
| Sr-91 | 9,5 час. | 0,749 (0,230); 1,024 (0,325) |
| La-140 | 40,22 час. | 0,329 (0,205); 0,487 (0,455); 0,816 (0,235); 1,597 (0,955) |
В ней в третьем столбце после значений энергии (в мегаэлектрон-вольтах) каждой спектральной линии в скобках показан выход данной реакции при одном распаде. На графике спектра выход каждой реакции будет определять высоту соответствующей спектральной линии. Примеры графиков спектров гамма-распада изотопов с одной и несколькими спектральными линиями представлены на рисунках 2.2 – 2.3.
Как видим, среди них есть весьма простые спектры, состоящие всего из одной или двух моноэнергетических линий. К таковым относятся спектры изотопов: I–131, I–133, I–135, показанные на рис. 2.2. Но есть и более сложные, состоящие из пяти и более спектральных линий: I-132, I-134, Br-82, показанные на рис. 2.3.
Нижняя граница энергий спектров всех, указанных в табл.2.1, короткоживущих изотопов составляет 0,329 МэВ (изотоп La-140). Верхняя граница энергий – 2,754 (изотоп Na-24).
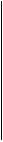

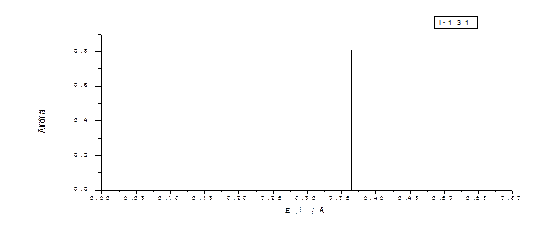


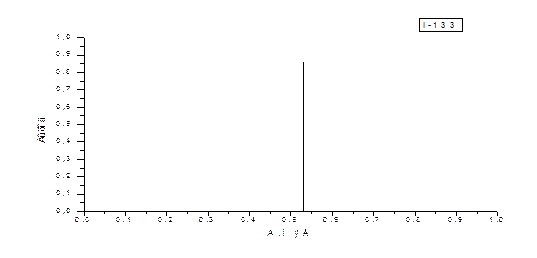
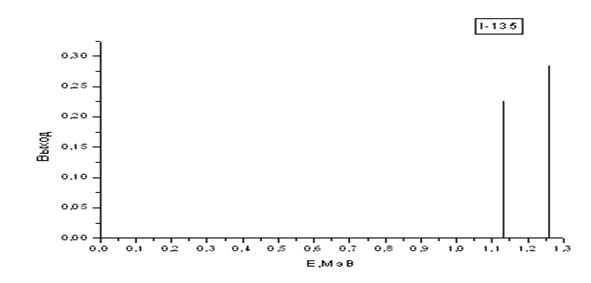
Рис. 2.2. Графики гамма-спектров изотопов I-131, I-133 и I-135
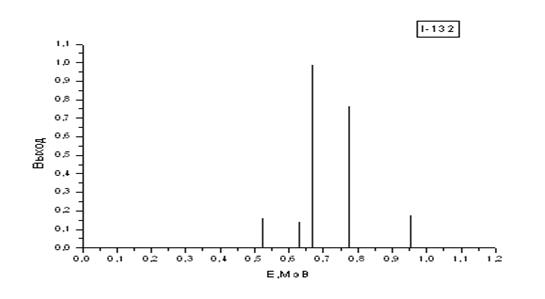
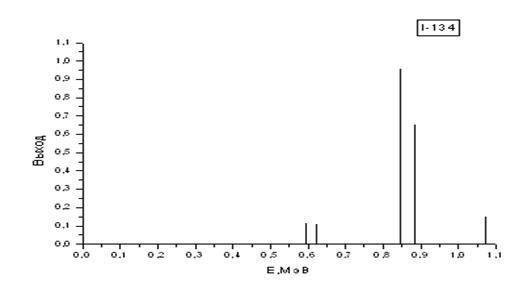
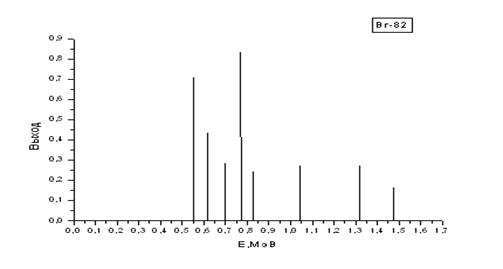
Рис. 2.3. Графики гамма-спектров изотопов I-132,I-134 и Br-82
Гамма-спектры основных долгоживущих изотопов ТРО представлены в таблице 2.2 [3, 5-7].
Таблица 2.2
Гамма-спектры основных долгоживущих изотопов ТРО
| Нуклид | Период полураспада | Энергия при гамма-распаде, МэВ (выход) |
| Am-241 | 432,2 лет | 0,0139 (0,427); 0,0595 (0,359); |
| Ba-133 | 10,5 лет | 0,081 (0,033); 0,276 (0,069); 0,303 (0,178); 0,356 (0,605); 0,384 (0,087); |
| Mn-54 | 312,7 сут. | 0,835 (0,9998) |
| Nb-95 | 35,06 сут. | 0,7658 (0,998) |
| Cs-134 | 2,062 лет | 0,563 (0,084); 0,569 (0,154); 0,605 (0,976); 0,796 (0,854); 0,802 (0,087) |
| Cs-137 | 30,17 лет | 0,6617 (0,9) |
| Co-58 | 70,8 сут. | 0,511 (0,299); 0.810 (0,994) |
| Co-60 | 5,271 лет | 1,173 (1,00); 1,333 (1,00) |
| Zr-95 | 64,02 сут. | 0,724 (0,437); 0,757 (0,553) |
| Fe-59 | 44,63 сут. | 1,099 (0,565); 1,292 (0,432) |
| Sb-125 | 2,77 лет | 0,176 (0,069); 0,428 (0,293); 0,463 (0,104); 0,607 (0,050) 0,635 (0,113) |
Здесь также имеются изотопы с простыми спектрами, представленными одной или двумя монолиниями (рис. 2.4, 2.5) и более сложные (рис. 2.6).
В практике радиационных измерений широко применяются образцовые источники гамма-излучения, особенно те, которые характеризуются моноэнергетическим излучением. К ним относятся изотопы 109Cd(энергия излучения 0,08803 МэВ, период полураспада 462,6 суток), 139Ce энергия излучения 0,16584 МэВ, период полураспада 140 суток), 113Sn(энергия излучения 0,2551 МэВ, период полураспада 115,09 суток), 137Сs (энергия излучения 0,6617 МэВ, период полураспада 30,17 лет), 55Mn(энергия излучения 0,835 МэВ, период полураспада 313 суток), 65Zn (энергия излучения 1,11544 МэВ, период полураспада 245 дней), 22Na (энергия излучения 1,2745 МэВ, период полураспада 2,6 года) [7]. Правда, нуклид 65Zn можно отнести к моноэнергетическим лишь условно, поскольку при массе источника достаточной для полного замедления выделяющихся при распаде позитронов излучаются ещё аннигиляционные гамма-кванты с энергией 0,511 МэВ, образующиеся при аннигиляции позитронов и электронов.


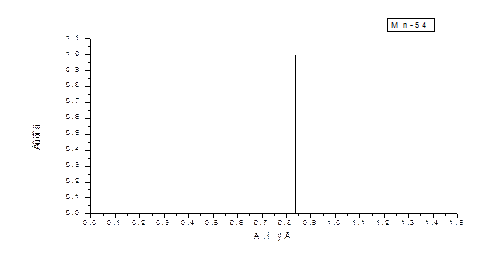




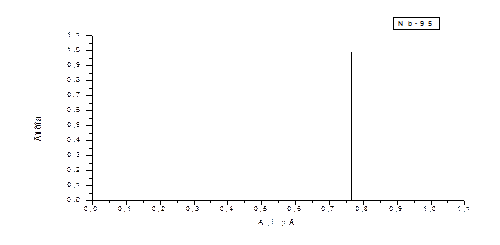
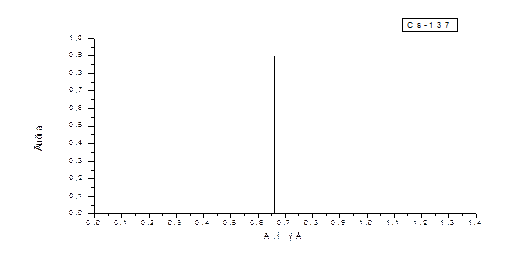
Рис. 2.4. Графики гамма-спектров изотопов Mn-54, Nb-95 и Cs-137

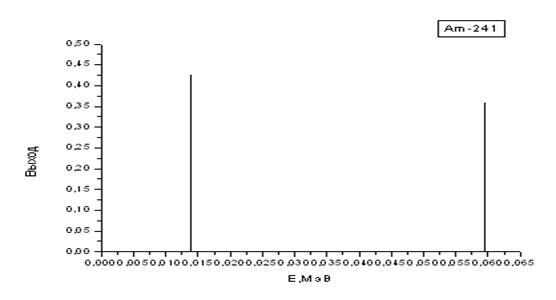
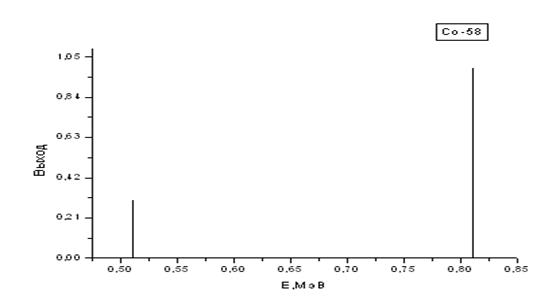
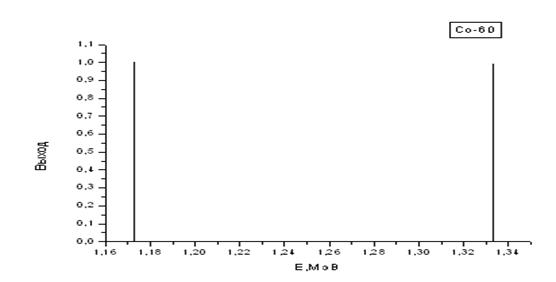
Рис. 2.5. Графики гамма-спектровизотопов Am-241, Co-58 и Co-60
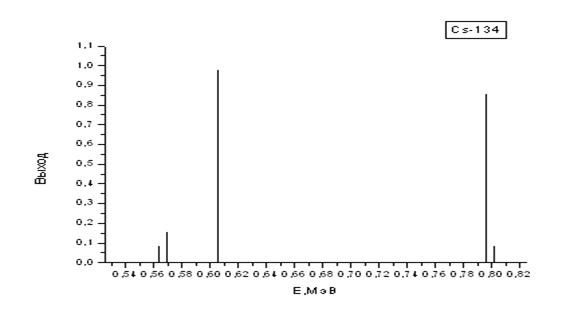
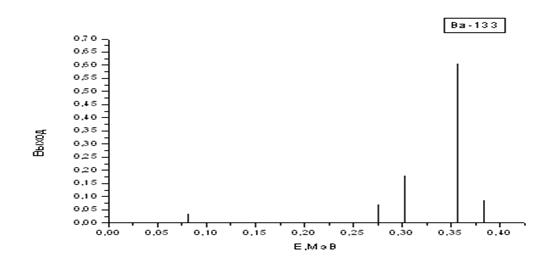
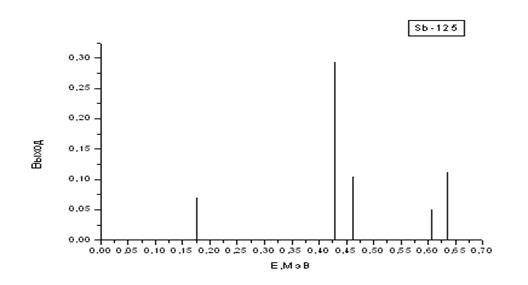
Рис. 2.6. Графики гамма-спектров изотопов Cs-134, Ba-133 и Sb-125
Но, помимо изотопов с моноэнергетическим гамма-излучением, для получения эталонных источников гамма-излучения с более детальной шкалой энергий применяются также изотопы с двумя и более линиями моноэнергетического излучения. Главным требованием для них является достаточно большой период полураспада. Основные из них представлены в таблице 2.3 [8].
Таблица 2.3
Эталонные источники гамма-излучения с несколькими линиями
моноэнергетического излучения
| Нуклид | Т1/2 | Е, МэВ | Нуклид | Т1/2 | Е, МэВ | |
| 241Am 57Со 109Gd 60Со | 458 лет 270 дней 453 дня 5,26 года | 0,01189 0,0139 0,0178 0,0208 0,05954 0,01436 0,12197 0,13633 0,0221 0,0250 0,0877 1,17323 1,33248 | 207Bi 182Tl | 30 лет 115 дней | 0,56963 1,76971 0,10010 0,15243 0,15639 0,17939 0,22211 0,22932 0,26407 1,12128 1,18903 1,22142 1,17323 0,56963 |
Помимо радиационных измерений радиоизотопные источники гамма-излучения широко применяются в медицине для лучевой терапии, в неразрушающем контроле различных материалов и изделий, в радиохимических и биологических исследованиях (метод «меченых атомов») и др.
Date: 2021-06-08; view: 1894; Нарушение авторских прав
§

Как уже отмечалось в п. 1.3 неустойчивые изотопы лёгких и средних элементов преимущественно подвержены бета-распаду. Если ядро имеет избыток нейтронов, то один из них испускает β–-частицу (т.е. электрон) и антинейтрино 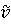 , превращаясь в протон. При этом порядковый номер изотопа увеличивается на единицу, а массовое число остаётся прежним, т.е. исходный элемент превращается в другой элемент с той же атомной массой. Если же ядро имеет избыток протонов, то происходит β -распад, т.е. один из протонов испускает позитрон (β -частицу) и нейтрино
, превращаясь в протон. При этом порядковый номер изотопа увеличивается на единицу, а массовое число остаётся прежним, т.е. исходный элемент превращается в другой элемент с той же атомной массой. Если же ядро имеет избыток протонов, то происходит β -распад, т.е. один из протонов испускает позитрон (β -частицу) и нейтрино 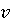 и превращается в нейтрон. При этом порядковый номер изотопа уменьшается на единицу, а массовое число остаётся прежним. Таким образом, при β-распаде мы всегда имеем превращение исходных элементов в соседние по порядковому номеру элементы, но с прежней атомной массой.
и превращается в нейтрон. При этом порядковый номер изотопа уменьшается на единицу, а массовое число остаётся прежним. Таким образом, при β-распаде мы всегда имеем превращение исходных элементов в соседние по порядковому номеру элементы, но с прежней атомной массой.
Испускаемые при β-распаде электроны и позитроны объединяются в одну группу бета-частиц. Они имеют равные массы и равные по абсолютной величине, но противоположные по знаку электрические заряды, т.е. позитрон является античастицей по отношению к электрону. Энергия, выделяемая при β-распаде, распределяется случайным образом между β-частицей и нейтрино (антинейтрино). Поэтому бета-излучение имеет сплошной спектр, т.е. энергия испускаемых β-частиц имеет непрерывное распределение от нуля до некоторой граничной энергии Емакс , определяемой энергией, выделяемой нуклоном при β-распаде. Для различных изотопов она различна, но не превышает 10 МэВ. Энергичные позитроны взаимодействуют с веществом аналогично электронам. Лишь когда позитроны практически полностью потеряют свою энергию, они аннигилируют с электронами, высвобождая энергию в виде гамма-квантов, энергия которых в соответствии с соотношением Эйнштейна равна Еγ = 2mec2, где me – масса электрона, с – скорость света в вакууме, что соответствует 1,022 МэВ.
Поскольку β-частицы являются заряженными частицами, то при прохождении через любое вещество они активно взаимодействуют с электронными оболочками атомов этого вещества и быстро теряют свою кинетическую энергию, после чего электроны захватываются атомами, приводя к их ионизации (образуются отрицательные ионы), а позитроны аннигилируют с ближайшими атомными электронами (что также приводит к ионизации этих атомов, образуя положительные ионы) с испусканием гамма-квантов с энергией 1,022 МэВ. Поэтому β-частицы имеют невысокую проникающую способность, что позволяет достаточно легко обеспечить эффективную защиту от прямого β-излучения. Основную опасность представляют β-активные аэрозоли, легко переносимые потоками воздуха и попадающие внутрь организма при дыхании, а также вместе с пылью оседающие на кожных покровах человека.
Поскольку радиоактивные изотопы подавляющего большинства элементов подвержены именно β-распаду, то любой мощный источник ионизирующего излучения (и, особенно, нейтронного излучения) приводит к появлению в окружающем пространстве радиоактивных изотопов тех веществ, которые окружают этот источник, включая и аэрозоли, которые всегда находятся в окружающей воздушной среде во взвешенном состоянии и в ещё большей концентрации в виде осевшей пыли покрывают поверхности всех окружающих предметов. Подавляющее большинство этих вторичных радиоактивных изотопов подвержены именно β-распаду и вместе с пылью различными путями могут попадать внутрь организма, приводя к тяжёлым последствиям. Поэтому защита от радиоактивных аэрозолей и во взвешенном, и в конденсированном состоянии представляет одну из важнейших задач обеспечения радиационной безопасности. Для определения концентрации β-активных аэрозолей в воздухе и загрязнения β-активными веществами кожных покровов и одежды персонала, а также поверхностей различных предметов создаются специальные приборы. Для их градуировки и испытаний очевидно необходимы образцовые источники β-излучения с известной активностью и средней энергией излучения.
Характеристики некоторых наиболее широко используемых радиоизотопных β-источников приведены в таблице 2.4 [3, 8] . В начале этой таблице приводятся изотопы, которые имеют только один β-переход (их называют «чистыми» β-излучателями), а в конце таблицы приведены изотопы имеющие по нескольку β-переходов.
Таблица 2.4
Характеристики β-излучения некоторых наиболее широко
применяемых радиоактивных нуклидов
| Нуклид и дочерний продукт | Т1/2 | Q, кэВ | Еβi, кэВ | n βi, % | 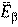 i, i,кэВ/β-частица | 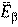 , ,кэВ/распад |
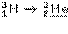 | 12,33 года | 18,57 | 18,6 | 5,7 | 5,7 | |
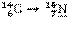 | 5730 лет | 156,47 | 156,5 | 49,4 | 49,4 | |
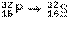 | 14,282 сут | 1710,4 | 1710,4 | 694,5 | 694,5 | |
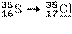 | 87,5 сут | 167,47 | 167,5 | 48,8 | 48,8 | |
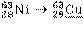 | 100,1 лет | 65,87 | 65,9 | 17,1 | 17,1 | |
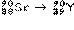 | 29,2 года | 196,1 | 196,1 | |||
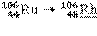 | 371,6 сут | 39,4 | 39,4 | 10,1 | 10,1 | |
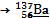 | 30 лет | 1173,2 | 511,5 1173,2 | 94,43 5,57 | 179,3 | |
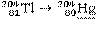 | 3,784 года | 763,4 | 763,4 | 97,45 | 237,4 | |
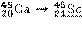 | 163,8 сут | 256,9 | 244,4 256,9 | 0,0019 99,9981 | 77,2 | |
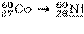 | 55,2709 лет | 2823,6 | 317,8 664,8 1491,1 | 99,92 0,005 0,08 | 96,2 | |
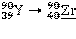 | 64,26 ч | 2279,2 | 518,5 2279,2 | 0,016 99,9885 | 930,6 |
В первой колонке приводится реакция распада, включая дочерний продукт. Если дочерний продукт является стабильным, то он подчёркивается. Во второй колонке – период полураспада Т1/2; в третьей – разность энергий между основными состояниями материнского и дочернего ядер Q, кэВ. В четвёртой и последующих колонках – данные об энергетическом спектре: Еβi – граничная частота β-спектра i-го β-перехода, т.е. максимальная энергия непрерывного спектра i-го β-перехода; n βi,% – выход β-частиц i-го β-перехода в процентах; 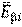 – средняя энергия спектра β-излучения i-го β-перехода на 1 β-частицу, кэВ/β-частица (средняя энергия β-частиц, определяемая по энергетическому спектру β-излучения i-го β-перехода);
– средняя энергия спектра β-излучения i-го β-перехода на 1 β-частицу, кэВ/β-частица (средняя энергия β-частиц, определяемая по энергетическому спектру β-излучения i-го β-перехода); 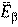 – средняя энергия спектра β-излучения на 1 распад ядра, кэВ/распад (средняя энергия β-частиц, определяемая по энергетическому спектру β-излучения данного радионуклида).
– средняя энергия спектра β-излучения на 1 распад ядра, кэВ/распад (средняя энергия β-частиц, определяемая по энергетическому спектру β-излучения данного радионуклида).
Графический вид спектров некоторых β-активных нуклидов, из перечисленных в таблице 2.4, приведен на рисунке 2.7 [3]. Здесь по оси ординат отложены значения спектральной плотности, пронормированные на 100 распадов (т.е. число β-частиц, приходящихся на энергетический интервал в 1 кэВ, излучаемых за 100 β-распадов). Из графиков следует, что на начальных участках спектральная плотность либо близка к равномерной, либо слабо растёт, затем идёт участок с более или менее плавным снижением спектральной плотности, а ближе к конечным участкам, где энергия β-частиц приближается к максимальной для данного изотопа спектральная плотность падает очень круто (почти вертикально).
Рис. 2.7. Энергетические спектры некоторых β-активных нуклидов
Date: 2021-06-08; view: 2271; Нарушение авторских прав
§

Основными радиоизотопными источниками α-излучения являются тяжёлые радиоактивные элементы: радий-226 и дочерние продукты его деления, полоний-210, плутоний-238, плутоний-239, актиний-227, америций-241, самарий-242.
Радий-226 исторически был самым первым обнаруженным радиоактивным элементом, но и сейчас он используется достаточно широко. Радий-226 в процессе α-распада последовательно проходит целый ряд превращений:
226Ra→222Rn→218Po→214Po→210Po→206Pb в конечном итоге превращаясь в нерадиоактивный свинец 206Pb. На каждом этапе этих превращений излучается одна α-частица, но каждой реакции соответствует своя энергия α-частиц и свой период полураспада. Характеристики α-распада 226Ra и его дочерних продуктов представлены в таблице 2.5 [5].
Таблица 2.5
Основные характеристики α-распада 226Ra и его дочерних продуктов
| Исходный изотоп | Реакция α-распада | Энергия α-частиц, МэВ | Период полураспада |
| 226Ra | 226Ra→222Rn α | 4,777 | 1622 года |
| 222Rn | 222Rn→218Po α | 5,486 | 3,825 суток |
| 218Po | 218Po→214Po α 2e | 5,998 | 3,05 мин |
| 214Po | 214Po→210Po α 2e | 7,680 | 164 мкс |
| 210Po | 210Po→206Pb α | 5,298 | 138,4 суток |
| 206Pb | Устойчивый | – | – |
Примечание: Полная схема распада226Ra кроме реакций α-распада включает и реакции β-распада со своими дочерними продуктами.
Наличие нескольких дочерних продуктов α-распада, также подверженных α-распаду с резко отличными периодами полураспада, приводит к нестабильности величины активности радиевых источников во времени и нестабильности его энергетического спектра, поскольку каждый из дочерних продуктов испускает α-частицы с энергией, существенно отличной как от энергии α-частиц 226Ra,так и от энергии α-частиц, испускаемых другими дочерними продуктами. Поэтому радиевые источники не используют в качестве образцовых источников α-излучения. В качестве таковых преимущественно используют плутониевые и другие источники.
Плутоний получают путём облучения нейтронами 238Uв ядерном реакторе. 239Puимеет период полураспада 24360 лет, что обеспечивает долговременную стабильность его активности: за 20 лет его активность уменьшается всего на 0,14 %. Однако, такая высокая стабильность обеспечивается лишь в случае высокой изотопной однородности источника. Дело в том, что при облучении урана-238 нейтронами, помимо изотопа 239Pu в небольших количествах образуются изотопы 241Pu, 240Pu и 238Pu. Но если небольшие примеси 240Pu и 238Pu не приводят к заметным изменениям активности источника, поскольку период полураспада этих изотопов весьма велик (6580 лет у 240Pu и 86,4 года у 238Pu), то примеси изотопа 241Puмогут приводить к существенно большей нестабильности источника за счёт накопления изотопа 241Am. Этот изотоп образуется в результате β-распада 241Pu(период полураспада 12,9 года), и сам является активным α-источником с периодом полураспада 458 лет. Постепенное накопление в источнике 241Amприводит к небольшому росту активности источника. Энергия α-частиц, излучаемых при распаде 239Pu, составляет примерно 5,1 МэВ. Энергия α-частиц, излучаемых при распаде 241Am, составляет 5,47МэВ. При распаде 238Puбольшая часть испускаемых α-частиц (71%) имеет энергию 5,5 МэВ, а остальные 28 % – энергию 5,46 МэВ.
Более детальные сведения о нуклидах, являющихся источниками α-излучения, приведены в таблице 2.6 [8].
В настоящее время в качестве образцовых источников α-излучения преимущественно используют плутониевые источники из изотопов 239Pu и 240Pu. Они излучают α-частицы примерно одинаковой энергии ~5,1 МэВ, обладают близкими периодами полураспада, что позволяет использовать любые смеси этих изотопов для создания источников α-излучения.
Таблица 2.6
Нуклиды, используемые как источники α-излучения
| Нуклид | Период полураспада | Энергия интенсивных α-групп, МэВ | Относительная интенсивность, % |
| 146Sm 150Gd 148Gd 232Th 238U 235U | 7∙107 лет 2,1∙106 лет 84 года 1,41∙1010 лет 4,5∙109 лет 7,1∙108 лет | 2,46±0,02 2,73±0,01 3,18±0,01 4,011±0,005 4,200±0,005 4,214±0,003 4,394±0,002 4,438±0,003 4,550±0,003 | 5,5 |
| 236U 230Th | 2,39∙107 лет 8,0∙104 лет | 4,493±0,003 4,6175±0,0015 4,6840±0,0015 | |
| 234U 237Np | 2,4∙105 лет 2,14∙106 лет | 4,7736±0,002 4,787±0,002 | |
| 233U | 1,62∙105 лет | 4,7829±0,0012 4,8236±0,0012 | |
| 241Pu | 5,6∙105 лет | 4,853±0,0015 4,896±0,0015 | |
| 242Pu | 3,73∙105 лет | 4,856±0,002 4,900±0,002 | |
| 231Pa | 3,25∙104 лет | 4,950±0,001 5,013±0,001 5,057±0,001 | |
| 239Pu | 2,44∙104 лет | 5,1055±0,0008 5,1433±0,0008 5,1556±0,0008 | |
| 240Pu | 6,58∙103 лет | 5,1233±0,0007 5,1677±0,0007 | |
| 243Am | 7,95∙103 лет | 5,233±0,001 5,275±0,001 | |
| 241Am | 458 лет | 5,442±0,001 5,484±0,001 | |
| 250Cf | 13,2 года | 5,9891±0,0006 6,0308±0,0006 | |
| 252Cf | 2,646 года | 6,0757±0,0005 6,1183±0,0005 | |
| 249Cf | 360 лет | 5,760±0,001 5,813±0,001 6,194±0,0007 |
Для создания миниатюрных источников α-излучения с высокой активностью используются калифорниевые источники с преобладанием изотопа 252Cf. При этом примеси других изотопов калифорния несущественно расширяют энергетический спектр испускаемых α-частиц.
Date: 2021-06-08; view: 1838; Нарушение авторских прав
§

Основными характеристиками источников нейтронного излучения являются:
– ядерная реакция, приводящая к образованию нейтронов;
– выход нейтронов;
– энергетический спектр;
– угловое распределение нейтронного излучения;
– интенсивность сопутствующего гамма-излучения.
Свободные нейтроны могут излучаться в результате различных реакций ядер вещества с заряженными частицами, гамма-квантами или в результате самопроизвольного деления некоторых тяжёлых ядер. Поэтому источники нейтронного излучения можно классифицировать по типу ядерной реакции и способу получения частиц, инициирующих эти реакции. В ядерно-физических, биологических и медицинских исследованиях наиболее часто используются радиоизотопные источники, состоящие из радиоактивных изотопов, излучающих заряженные частицы, и вещества с малой энергией связи нейтронов в ядре (чаще всего бериллия).
Источники, использующие (α, n)-реакцию. Наибольшее применение получили источники, использующие (α, n)-реакцию: 238Pu-α-Be, 239Pu-α-Be, 210Po-α-Be,226Ra-α-Be. С последней из перечисленных реакций связано открытие нейтронов:
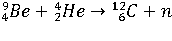 . (2.8)
. (2.8)
Эти источники представляют собой однородную спрессованную смесь α-излучателя с порошком металлического бериллия в герметичной упаковке. Кроме бериллия в качестве мишени для испускаемых α-частиц иногда применяют бор, фтор или литий, но наибольший выход нейтронов достигается при использовании бериллия. Размеры (α, n)-источников невелики и для большинства задач их можно считать точечными. Для обеспечения более изотропного выхода нейтронов их делают сферической формы. Но технологически более простыми, а потому и более широко применяемыми являются источники цилиндрической конструкции.
Все эти источники являются источниками быстрых нейтронов: первый из них (238Pu-α-Be) характеризуется энергией, соответствующей максимуму спектральной плотности нейтронов Емакс = 11,1 МэВ и средней энергией нейтронов3,9 МэВ, второй (239Pu-α-Be) – Eмакс = 10,7 МэВ и средней энергией 4,5 МэВ, третий (210Po-α-Be) характеризуется Eмакс = 10,9 МэВ и средней энергией 4,2 МэВ, четвёртый (радиевый) имеет Eмакс = 13 МэВ и среднюю энергию 3,2 МэВ [9-12]. Следует учитывать, что в источниках, использующих в качестве α-излучателя 226Raизлучают альфа-частицы как собственно 226Ra, так и промежуточные продукты его распада. Поэтому выход нейтронов источника в течение первых 20-30 суток после его изготовления увеличивается за счёт накопления в нём дочерних продуктов распада 226Ra, являющихся дополнительными источниками α-частиц. Затем, в первые годы после его изготовления, происходит более медленное увеличение выхода нейтронов (примерно на 0,5 % в год) [9].
Периоды полураспада у этих источников соответствуют: для 238Pu– 87 лет, для 239Pu – 24360лет, для 210Pо– 138,5 суток и для радиевого 1600 лет. Таким образом, наименьшим периодом полураспада характеризуется полониевый источник, но благодаря этому он имеет наибольший выход нейтронов: на 1 г радионуклида – 1010 нейтронов/с. Поэтому такие источники применяют в тех случаях, когда необходимо получить нейтронные поля высокой интенсивности. Во всех других случаях предпочтительными являются источники 239Pu-α-Be, поскольку выход нейтронов у них стабилен в течение многих лет, благодаря очень большому периоду полураспада – 24360 лет. Конечно, высокая стабильность источника обеспечивается только в случае высокой однородности изотопного состава источника. При этом необходимый выход нейтронов обеспечивается за счёт соответствующего количества нуклида в источнике.
Энергетические спектры всех (α, n)-источников непрерывны, поскольку при столкновении α-частицы с ядром атома мишени (в частности, бериллия)кинетическая энергия, переданная ядру отдачи, может быть различна. Кроме того, до столкновения с ядром атома бериллия альфа-частицы могут испытывать упругие и неупругие (ионизирующие) столкновения с атомами мишени, что приводит к различным потерям энергии α-частиц. Измерение энергетического спектра нейтронных источников в широком энергетическом диапазоне представляет собой сложную задачу. Поэтому выпускаемые промышленностью образцовые источники нейтронного излучения не аттестуются по спектральному составу нейтронного излучения. В литературе можно найти существенно отличающиеся по форме энергетические спектры для нейтронных источников одного и того же изотопного состава. В качестве примеров можно привести спектры наиболее широко используемых радиоизотопных источников нейтронов, представленные в [10] (рисунок 2.8), и спектры источников того же изотопного состава, представленные в [13]: рисунок 2.9 для источника 239Pu-Be и рисунок 2.10 для источника 252Cf. Конечно, здесь следует учесть, что в первом случае спектры представлены гладкими кривыми, а во втором случае являются ступенчатыми (в соответствии с теми энергетическими интервалами, для которых определялась спектральная плотность, измеренная многошаровым нейтронным спектрометром Боннера). Тем не менее, различия формы соответствующих спектров отчётливо видны. В частности, на рисунке 2.8 на спектре Pu–Be-источника отчётливо виден второй максимум, соответствующий энергии 200-300 кэВ, а на рисунке 2.9 для того же источника его нет. Если на рисунке 2.8 спектральная плотность уменьшается до нуля уже при энергиях ниже 70 кэВ, то на рисунке 2.9 виден отчётливый рост спектральной плотности в области тепловых энергий (ниже 0,4 эВ). Более того, спектры, восстановленные по одним и тем же данным измерений, но с использованием двух различных программ также заметно отличаются друг от друга.
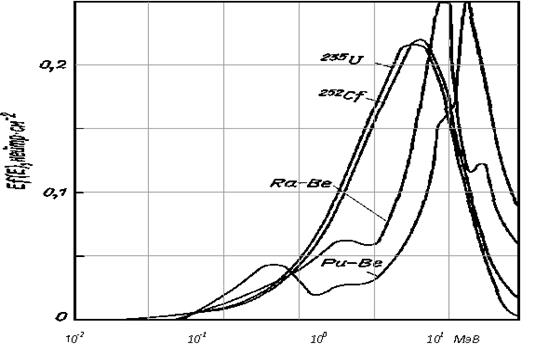
Рис. 2.8. Энергетические спектры радиоизотопных источников
нейтронов по [10]
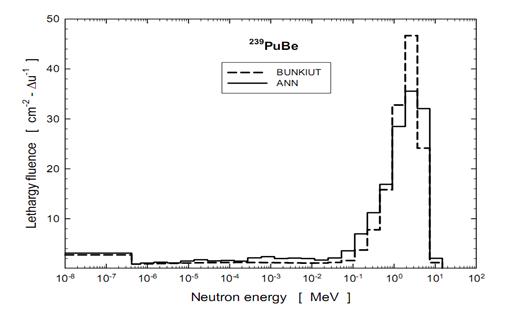
Рис. 2.9. Энергетические спектры источника 239Pu-Be,
измеренные многошаровым спектрометром Боннера [13]
(Восстановление спектров на компьютере проводилось с использованием
двух различных программ BUNKIUT и ANN)
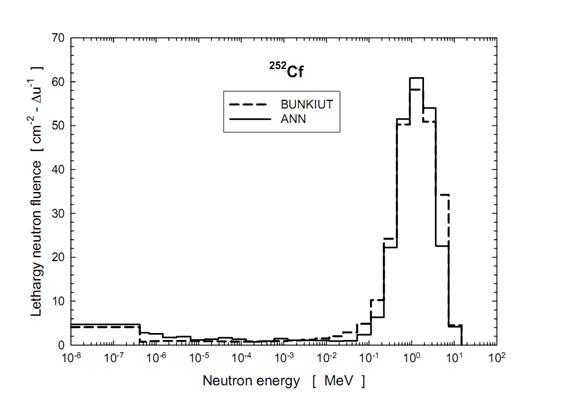
Рис. 2.10. Энергетические спектры источника 252Cf,
измеренные многошаровым спектрометром Боннера [13]
(Восстановление спектров на компьютере проводилось с использованием
двух различных программ BUNKIUT и ANN)
Для калифорниевого источника различия не столь существенны: на обоих рисунках мы имеем спектры с одним максимумом в области энергий 1-3 МэВ. Но на рисунке 2.10 отчётливо представлен рост спектральной плотности в области тепловых энергий, тогда как на рисунке 2.8 его не наблюдается. Интересно сопоставить эти спектры со спектром калифорниевого источника, представленным в [9] (рис. 2.15). Здесь, правда, необходимо учесть, что шкала энергий представлена в линейном (а не логарифмическом, как на предыдущих рисунках) масштабе, поэтому низкоэнергетическая часть спектра практически не видна. Однако отчётливо видно, что максимум спектральной плотности здесь сдвинут в сторону меньших энергий и соответствует 0,8-1,0 МэВ, тогда как на рисунках 2.8 и 2.10 он соответствует 2,0-2,5 МэВ.

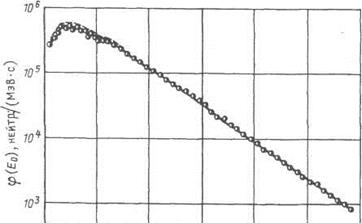 0 2 4 6 810 E0, МэВ
0 2 4 6 810 E0, МэВ
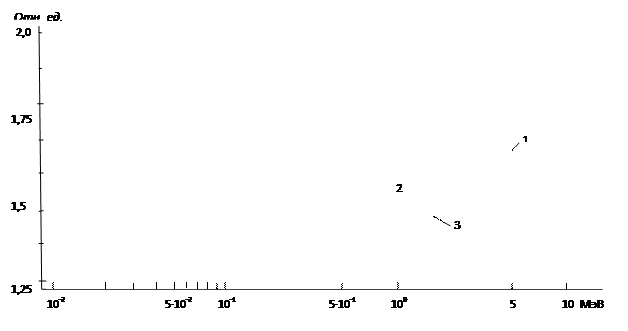
Рис. 2.11. Энергетический спектр нейтронов радионуклидного
источника на основе 252Cf :
ооо — для источника в виде иглы диаметром 1,7 и высотой 36 мм;
 – для того же источника в стальном цилиндре
– для того же источника в стальном цилиндре
 Но, если в рассмотренных выше спектрах ещё можно обнаружить что-то общее, то спектры, приведенные в [15] для плутоний-бериллиевых и калифорниевых образцовых источников (рисунки 2.12 и 2.13), практически ничего общего с вышеприведенным спектрами не имеют.
Но, если в рассмотренных выше спектрах ещё можно обнаружить что-то общее, то спектры, приведенные в [15] для плутоний-бериллиевых и калифорниевых образцовых источников (рисунки 2.12 и 2.13), практически ничего общего с вышеприведенным спектрами не имеют.
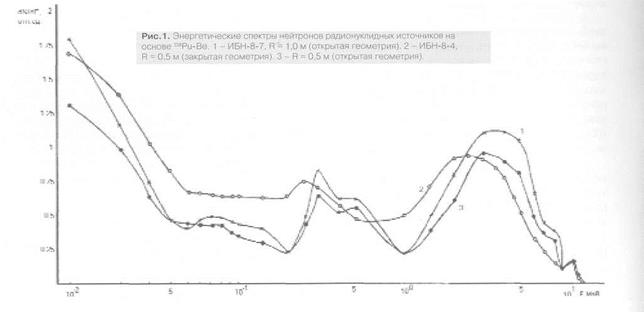
Рис. 2.12. Энергетические спектры нейтронных источников
на основе 239Pu-Be[15]:
1– ИБН-8-7, R = 1 м (открытая геометрия); 2 – ИБН-8-4, R = 0,5 м (закрытая геометрия);
3– ИБН-8-4, R = 0,5 м (открытая геометрия)
Рис. 2.13. Энергетические спектры образцовых радионуклидных
нейтронных источников на основе 252Cf [15]:
1 – ИНК-5, R = 1 м (открытая геометрия); 2 – ИНК-2, R = 0,5 м (закрытая геометрия)
Из представленных на рисунке 2.12 спектров источников на основе 239Pu-Be нас будут интересовать спектры, снятые для источников в открытой геометрии (кривые 1 и 3). В целом, они подобны друг другу, но резко отличаются от вышеприведенных спектров для плутоний-бериллиевых источников. Действительно, они имеют два отчётливых максимума: один (главный) в области энергий 4-5 МэВ, второй соответствует энергии 0,3 МэВ, а для энергий ниже 0,04 МэВ имеет место весьма резкий рост спектральной плотности, которая уже для энергии 0,01 МэВ превышает спектральную плотность для главного пика. Ничего подобного на рисунках 2.8 и 2.9 мы не имеем (причём, все эти спектры представлены в логарифмическом масштабе по шкале энергий).
Низкая достоверность измерений энергетических спектров образцовых источников нейтронов существенно осложняет метрологическое обеспечение нейтронной спектрометрии. На сегодняшний момент оно фактически отсутствует.
Важной характеристикой источников нейтронного излучения является интенсивность сопутствующего фотонного излучения. Её принято характеризовать числом фотонов на один испускаемый нейтрон. Для всех указанных источников кроме радиевого оно составляет 1-3 фотона/нейтрон. Лишь для радиевого источника оно много больше – примерно 104 фотонов/нейтрон. Это ещё один существенный недостаток радиевых источников.
Учитывая совокупность характеристик нейтронных источников, использующих реакцию (n, α), в качестве образцовых источников нейтронного излучения используют преимущественно источники 239Pu-Beи 238Pu-Be [12].
Источники нейтронов, использующие реакции спонтанного деления. Природными источниками нейтронов являются изотопы, испытывающие спонтанное деление с вылетом нейтронов. Такими природными изотопами являются 238U, 235U и 242Th.Но у них очень мал выход нейтронов: для 238U он составляет 6,9∙10-3 нейтрон/(с∙г), для 235U – 3∙10-4 нейтрон/(с∙г) и для 242Th – 4,2∙10-5 нейтрон/(с∙г) [11]. Поэтому для получения выхода нейтронов хотя бы в единицы нейтрон/(с∙г) пришлось бы увеличивать массу активного вещества источника до нескольких килограмм. Это исключает возможность использования природных делящихся веществ в качестве образцовых источников нейтронов.
Освоение технологии получения в достаточных количествах трансурановых элементов позволило осуществить создание источников нейтронов, использующих реакцию самопроизвольного деления с вылетом нейтронов (конечно, с количеством делящегося вещества много меньшим критической массы, при которой возникает цепная реакция) на основе нуклидов: 242Cm(кюрий)244Cm и 252Cf . Особенно перспективными и удобными являются источники нейтронов на основе изотопа 252Cf. Этот изотоп имеет две ветви распада: α-распад с периодом полураспада 2,64 года и реакция деления с вылетом нейтронов с периодом спонтанного полураспада 82 года. Именно вторая из этих реакций и используется для создания источников нейтронного излучения. Эти источники обладают исключительно высоким выходом нейтронов: 2,6∙1012 нейтрон/с на 1 г активного вещества. Это позволяет изготавливать буквально невесомые источники с количеством изотопа в доли миллиграмма. Активное вещество помещается в стальной герметичный корпус, который полностью поглощает альфа-частицы, но свободно пропускает нейтроны. Энергетический спектр нейтронов этого источника достаточно гладкий и (в линейном масштабе) хорошо описывается уравнением [3]:
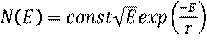 , (2.9)
, (2.9)
где Т – средняя температура спектра, Т = 1,40±0,02 МэВ.
Среднее число мгновенных нейтронов на деление у этого источника составляет 3,78 с малым выходом сопутствующего излучения (обычно не более трёх фотонов на один испущенный нейтрон).
Следует, однако, иметь в виду, что и выход нейтронов, и его энергетическое распределение, и интенсивность сопутствующего гамма-излучения зависят от чистоты изотопа, а также размеров и материала герметичной упаковки источника. Это видно и из приведенного рисунка 2.11, где спектр «голого» источника несколько отличается (особенно в низкоэнергетической части) от спектра того же источника, помещённого в стальной корпус.
Источники спонтанного деления наиболее перспективны для создания образцовых источников со стабильным энергетическим спектром излучаемых нейтронов, поскольку в них не происходит смешивания материалов (как это имеет место в (α, n)-источниках), а потому выход нейтронов и их энергетический спектр стабильны.
Основные свойства применяемых на практике источников нейтронов спонтанного деления приведены в таблице 2.7 [11]. Данная таблица показывает, что все указанные источники кроме 254Cfподвержены не только спонтанному делению с вылетом нейтронов, но и α-распаду, причём скорость α-распада на много порядков превышает скорость спонтанного деления. Это означает, что указанные источники являются источниками смешанного излучения – нейтронов и α-частиц, причём α-излучение во много раз интенсивнее нейтронного. Исключение составляют калифорниевые источники.
Таблица 2.7
Характеристики нейтронных источников спонтанного деления
| Изотоп | Период полураспада | Отношение скоростей α-распада и спонтанного деления | Число нейтронов на одно деление | Выход нейтронов, n/(с∙г) | |
| спонтанного деления | α-распада | ||||
| 238U | 8,3∙1015лет | 4,51∙109лет | 1,8∙106 | 2,2±0,3 | – |
| 236Pu | 3,5∙109лет | 2,7 года | 1,3∙109 | 1,89±0,20 | 3,1∙104 |
| 238Pu | 4,9∙1010лет | 89,6 года | 5,5∙108 | 2,04±0,10 | 2,3∙103 |
| 240Pu | 1,2∙1011лет | 6580 лет | 1,9∙107 | 2,257±0,046 | 7,0∙102 |
| 242Pu | 7,3∙1010лет | 3,78∙105лет | 1,9∙105 | 2,18±0,09 | – |
| 242Cm | 7,2∙106лет | 162,5 суток | 1,6∙107 | 2,65±0,09 | 1,8∙109 |
| 244Cm | 1,4∙107лет | 18,4 года | 7,6∙105 | 2,60±0,12 | 1,0∙107 |
| 252Cf | 66 лет | 2,2 года | 3,82±0,12 | 2,6∙1012 | |
| 254Cf | 60 суток | – | 3,5 | – |
Изотоп 254Cf вообще не подвержен α-распаду, а для изотопа 252Cfинтенсивность α-излучения всего в несколько раз превышает интенсивность нейтронного (здесь следует учитывать, что при одном акте α-распада вылетает лишь одна α-частица, а при одном акте спонтанного деления испускается в среднем 3,82 нейтрона). Но у изотопа 254Cf слишком мал период полураспада (всего 60 суток), поэтому для использования в качестве образцового источника он не пригоден. К тому же его сложнее получать. Таким образом, наиболее перспективными являются источники, использующие изотоп 252Cf. А поскольку радиоактивный изотоп в применяемых на практике источниках всегда помещают в герметичный металлический корпус, то подавляющая часть сопутствующего α-излучения будет поглощаться этим корпусом. Источники на основе 252Cf особенноудобны для проведения различных методических и калибровочных исследований. Малые размеры источника практически исключают возмущение исследуемой среды в задачах распространения нейтронов в веществе, а большая его мощность (до 1010 нейтр/с) позволяет рассматривать задачи с большой кратностью ослабления.
Источники нейтронного излучения, использующие (γ, n)-реакцию (фотонейтронные источники). Радиоизотопными источниками нейтронов более низких энергий служат источники, использующие (γ, n)-реакцию. Поскольку эта реакция может происходить только при энергии гамма-квантов, превышающей энергию связи нейтронов в ядрах атомов мишени, а энергия гамма-излучения большинства радиоизотопных источников не превышает 3 МэВ, то в качестве мишеней в таких источниках могут использоваться вещества с энергией связи нейтронов менее 3 МэВ: бериллий с энергетическим порогом реакции 1,665 МэВ и дейтерий с энергетическим порогом 2,227 МэВ [3, 5]. Бериллий применяется в чистом виде, а дейтерий – в виде оксида дейтерия D2O. Источниками фотонов (гамма-квантов) могут служить радиоактивные изотопы: 24Na, 56Mn, 72Ga, 88Y, 116In, 124Sb, 140La, а также 226Ra в равновесии с основными дочерними продуктами распада. Основные характеристики наиболее широко применяемых фотонейтронных источников приведены в таблице 2.8. В ней в третьем столбце приведены энергия Еγ и квантовый выход nγ (в скобках) для основных фотонов, на которых идёт реакция. В четвёртом столбце приведена средняя энергия вылетающих нейтронов, а в последнем столбце – выход нейтронов на 1 г мишени, находящейся на расстоянии 1 см от источника активностью 3,7∙1010 Бк (1 Ku).
Все гамма-нейтронные источники характеризуются сравнительно небольшим разбросом энергии излучаемых нейтронов. Поэтому для многих практических задач спектры этих источников можно считать моноэнергетическими.
Более точно энергетический спектр гамма-нейтронных источников может быть определён расчётным путём. При облучении бериллия или оксида дейтерия моноэнергетическими фотонами с энергией Еγ (МэВ) энергия нейтронов Еп (МэВ), испускаемых под углом θ к направлению движения фотонов, может быть вычислена по формуле [5]:
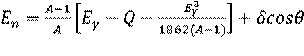 , (2.10)
, (2.10)
где А – атомная масса мишени;
Q – энергия связи нейтронов в ядре мишени, МэВ (для бериллия Q = 1,665 МэВ, для дейтерия Q = 2,227 МэВ);
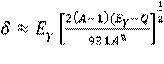 . (2.11)
. (2.11)
Таблица 2.8
Основные характеристики фотонейтронных источников
| Источник | Т1/2 | Еγi , МэВ (nγi , %) | En , МэВ | N∙104 нейтр/с |
| 24Na Be | 15,029 ч | 3,867 (0,06) 2,754 (99,87) | 0,83 | |
| 24Na D2O | 15,029 ч | 3,867 (0,06) 2,754 (99,87) | 0,22 | |
| 88Y Be | 107,15 сут | 3,219 (0,01) 2,734 (041) 1,836 (99,6) | 0,16 | |
| 88Y D2O | 107,15 сут | 3,219 (0,01) 2,734 (0,43) | 0,31 | 0,3 |
| 124Sb Be | 60,2 сут | 2,091 (5,61) 1,691 (49) | 0,024 | |
| 140La Be | 1,67 сут | 2,522 (3,44) 2,348 (0,86) | 0,62 | 0,3 |
| 140La D2O | 1,67 сут | 2,522 (3,44) 2,348 (0,86) | 0,15 | 0,8 |
| Ra Be | 1600 лет | 2,448 (1,65) 2,204 (5,3) 1,847 (2,2) 1,764 (16,6) | 0,6 | 3,0 |
| Ra D2O | 1600 лет | 2,448 (1,65) | 0,12 | 0,1 |
Подставляя в эти формулы числовые значения А, Q и Eγдля конкретного источника можно вычислить энергии нейтронов для каждой гамма-линии используемого в источнике гамма-активного изотопа и с учётом квантового выхода каждой гамма-линии вычислить результирующий спектр излучаемых нейтронов. Согласно этой формуле разброс энергии нейтронов таких источников невелик и для ряда практических задач такие источники можно считать моноэнергетическими. В этом случае приближённо энергию нейтронов можно оценивать как
Еn ≈ Еγ – Q . (2.12)
Но в действительности фактический разброс энергий нейтронов у таких источников больше, чем расчётный по формуле (2.10). Это обусловлено замедлением некоторых вылетевших нейтронов при упругих столкновениях с ядрами атомов бериллия или дейтерия (это весьма лёгкие ядра и поэтому, при столкновении с ними нейтроны могут терять значительную энергию). Второй причиной может служить частичная потеря энергии фотонами до того, как происходит (γ, n)-реакция, за счёт комптоновского рассеяния. Оба эти фактора действуют тем сильнее, чем больше масса и размеры источника. Кроме того, как следует из таблицы 2.8, все изотопы, используемые в качестве источников первичного гамма-излучения, могут излучать гамма-кванты нескольких дискретных значений энергии (причём, в таблице показаны только те, которые выше пороговой для (γ, n)-реакции). Поэтому указанные в 4-м столбце данной таблицы значения энергии нейтронов данных источников являются усреднёнными, соответствующими пиковым значениям спектральной плотности (при этом нейтроны, порождённые гамма-квантами с малым удельным вкладом, которые будут иметь существенно отличную энергию, в расчёт не принимаются).
Получить источники с необходимым выходом нейтронов можно варьированием его активной массы. Поэтому меньшая удельная активность этих источников по сравнению с (α, n)-источниками не является их существенным недостатком. Более существенным недостатком является большой гамма-фон этих источников.
Таким образом, основным достоинством источников нейтронов, использующих (γ, n)-реакцию, является возможность получения «почти» моноэнергетических нейтронов в достаточно широком диапазоне дискретных значений от 0,83 МэВ до 24 кэВ, а основным недостатком – высокий гамма-фон.
Date: 2021-06-08; view: 7553; Нарушение авторских прав
§

Нейтроны возникают в любых мишенях при их бомбардировке заряженными частицами, если только их энергия превышает энергию связи нейтронов в ядре мишени. Наилучшими по выходу нейтронов являются мишени из лёгких элементов: бериллия, дейтерия, трития. В качестве разгоняемых заряженных частиц чаще всего используются протоны и дейтроны.
Диапазон энергии нейтронов, который может быть получен в этих реакциях, составляет от нескольких кэВ до 20 МэВ. Большим достоинством таких нейтронных источников является возможность изменять энергию нейтронов путём изменения энергии заряженных частиц с помощью ускорителя.
На рисунке 2.14 [3, 5] представлены зависимости энергии нейтронов от энергии заряженных частиц (протонов и дейтронов), бомбардирующих различные мишени (дейтерий, тритий и литий). Здесь рассмотрены только нейтроны, вылетающие под углами 00 и 1800 по отношению к направлению бомбардирующих частиц. Из данного рисунка следует, что при бомбардировке дейтронами дейтериевой и тритиевой мишеней пороговая энергия равна нулю и энергия нейтронов мало зависит от энергии бомбардирующих частиц (дейтронов). Но при бомбардировке протонами реакция начинается с пороговой энергии протонов (для тритиевой мишени примерно 1,1 МэВ, для литиевой – 2 МэВ) и энергия нейтронов скачком возрастает примерно до 0,3 МэВ, а далее, с ростом энергии бомбардирующих протонов возрастает уже более плавно, но круче, чем при бомбардировке дейтронами.
С помощью ускорителей заряженных частиц можно также получать фотоны высоких энергий (выше 6 МэВ), что невозможно получить от радиоизотопных источников. А это открывает возможности получения нейтронов с помощью (γ, n)-реакции не только на бериллии и дейтерии, но и на других элементах, у которых энергия связи нейтрона с ядром выше 6 МэВ. Такие высокоэнергичные гамма-кванты обычно получают на электронных ускорителях, бомбардируя пучком ускоренных электронов различные мишени.
Рис. 2.14. Зависимость энергии нейтронов от энергии ускоренных
протонов и дейтронов для углов вылета 00 и 1800 на тритиевых,
дейтериевых и литиевых мишенях
Сечение (γ, n)-реакции на ядрах различных элементов (кроме лёгких) с ростом энергии гамма-квантов сначала возрастает, достигая максимума примерно при 20 МэВ, а затем убывает. Но по сравнению с другими процессами взаимодействия фотонов со средой сечения фотонейтронных реакций на два-три порядка меньше.
Date: 2021-06-08; view: 1319; Нарушение авторских прав
§

При работе реактора его активная зона является источником интенсивного нейтронного и γ-излучения. Излучения других видов (α- и β-излучение, тормозное рентгеновское излучение), образующиеся в активной зоне, практически полностью поглощаются в ней и не выходят за её пределы. Тем более ими можно пренебречь за зоной биологической защиты реактора.
Нейтроны образуются в результате цепной реакции деления ядерного топлива (мгновенные нейтроны), а также испускаются сильно возбуждёнными ядрами дочерних продуктов деления (запаздывающие нейтроны). Мгновенные нейтроны испускаются в процессе деления ядер 235U, 233U, 239Pu, служащих ядерным топливом. За один акт деления выбрасывается в среднем от 2,5 до 2,9 нейтронов. Запаздывающие нейтроны образуются в существенно меньшем количестве (примерно в 300 раз) и испускаются ядрами дочерних продуктов деления с периодами полураспада от 0,18 до 54,5 с [5].
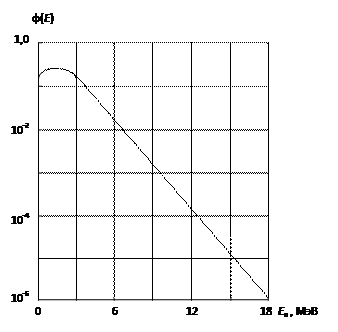
Средняя энергия нейтронов деления составляет примерно 2 МэВ, наиболее вероятная 0,6-0,8 МэВ, а максимальная 18 МэВ. Энергетический спектр нейтронов деления представлен на рисунке 2.15-a [5]..
 а) б)
а) б)
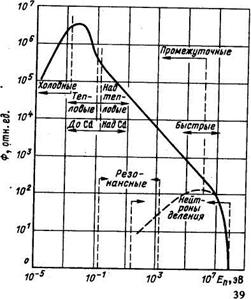
Рис. 2.15. Энергетические спектры нейтронов деления (а) и
суммарного нейтронного потока в активной зоне реактора (б)
В результате взаимодействия нейтронов с ядрами атомов материалов активной зоны спектр нейтронов изменяет свой вид: в области энергий быстрых нейтронов он практически совпадает со спектром нейтронов деления, в промежуточной области энергий – это спектр замедляющихся нейтронов (1/Е-спектр), т.е. линейно падающий с ростом энергии, а в тепловой и надтепловой областях он близок к максвелловскому спектру. Конечно, вид спектра зависит от состава и конструкции активной зоны, поэтому суммарный спектр нейтронов в активной зоне реактора, представленный на рисунке 2.15-б является примернымТочное знание спектра нейтронов на границах активной зоны важно для расчёта биологической защиты реактора, а также для правильного управления режимами его работы, поскольку именно в результате потерь энергии нейтронов в замедляющей среде активной зоны и выделяется основная часть энергии.
Гамма-излучение образуется в активной зоне работающего реактора в результате реакции деления ядер урана или плутония (мгновенное γ-излучение), а также при распаде короткоживущих продуктов деления и при захвате нейтронов ядрами различных веществ активной зоны (захватное γ-излучение). Полное количество энергии выделяющееся при одном акте деления в виде γ-излучения составляет 7,2-7,5 МэВ, которое излучается в виде одного или нескольких квантов. Энергетический спектр мгновенного γ-излучения описывается экспонентой [5]:
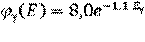 . (2.13)
. (2.13)
Короткоживущими принято считать дочерние продукты распада реакции деления, которые распадаются с испусканием γ-квантов с периодом полураспада до 10 минут. Общее количество таких γ-квантов (в расчёте на один акт деления ядер исходного топлива) примерно соответствует количеству мгновенных γ-квантов. Каждый дочерний продукт деления испускает γ-кванты в количестве и с энергией, характерными именно для данного продукта. Поэтому спектры этих излучений являются дискретными. Но поскольку таких дочерних продуктов в цепочках распадов много, то суммарное энергетическое распределения этого излучения также описывается экспонентой [5]:
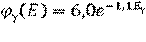 . (2.14)
. (2.14)
Таким образом спектр суммарного мгновенного и захватного γ-излучения также будет описываться экспонентой:
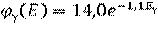 . (2.15)
. (2.15)
Захватное γ-излучение образуется в результате захвата нейтронов ядрами любых веществ. При этом возникает неустойчивое возбуждённое ядро, которое испускает избыточную энергию в виде γ-квантов или за счёт испускания других частиц (а чаще происходит и то, и другое). Таким образом источником захватного γ-излучения могут быть ядра атомов любых материалов из которых состоит активная зона. Спектр этого излучения также является дискретным.
Таким образом, суммарное γ-излучение активной зоны характеризуется непрерывным экспоненциально спадающим с ростом энергии спектром, на фоне которого можно обнаружить наиболее интенсивные пики захватного излучения. Максимальная энергия суммарного γ-излучения не превышает 10 МэВ.
Кроме самой активной зоны реактора источником ионизирующих излучений является технологический контур АЭС.
В настоящее время находящиеся в эксплуатации АЭС работают либо по одноконтурной, либо по двухконтурной схеме. Лишь реакторы на быстрых нейтронах работают по трёхконтурной схеме. По одноконтурной схеме работают реакторы РБМК-1000 (Курская, Ленинградская и Смоленская АЭС), по двухконтурной – ВВЭР-440, ВВЭР-1000 (Балаковская, Волгодонская, Калининская, Кольская и Нововоронежская АЭС), на быстрых нейтронах БН-600 (Белоярская АЭС). Речь здесь идёт о замкнутых контурах теплоносителя. Проходя через активную зону ядерного реактора, теплоноситель (во всех указанных реакторах кроме первого контура реактора на быстрых нейтронах это обычная вода) вода вскипает, превращается в перегретый пар и под давлением подаётся на паровую турбину в одноконтурных реакторах или на парогенератор (фактически теплообменник) в двухконтурных реакторах. После турбины пар используется для предварительного нагрева воды, циркулирующей в первом контуре или для нагрева воды в системе теплоснабжения (если АЭС служит не только для выработки электричества, но и для выработки тепла). Это позволяет с пользой утилизировать сохранившееся тепло в отработанном паре. После теплообменника пар поступает в конденсатор, где конденсируется в воду и она вновь насосами подаётся в активную зону реактора. Сам теплоноситель и содержащиеся в нём примеси (хотя в контуре предусмотрена непрерывная водоочистка, но примеси всё равно остаются), попадая в процессе циркуляции в активную зону реактора, интенсивно облучаются нейтронами и становятся радиоактивными. При распаде радиоактивных ядер выделяется гамма- и другие виды ионизирующих излучений. Однако вследствие малой проникающей способности α- и β-излучения эти виды излучений не выходят за пределы оборудования технологического контура, поэтому технологический контур АЭС можно считать источником только γ-излучения. Дополнительными источниками радиации в теплоносителе являются продукты деления ядерного топлива, проникающие из ТВЭЛов при нарушении герметичности их оболочек. На внутренних стенках оборудования контура теплоносителя (трубопроводы, задвижки, насосы и т.п.) образуются радиоактивные отложения из примесей, содержащихся в теплоносителе (растворённый в воде натрий, продукты коррозии различных элементов технологического контура, вещества поверхностных загрязнений ТВЕЛов и т.д.).
Собственная активность теплоносителя – воды (радиоактивные ядра, образующиеся из ядер кислорода при облучении нейтронами, водород не активируется) может достигать величины 3∙109 Бк/кг (0,1 Ки/кг). Собственная активность расплавленного натрия, который является теплоносителем в первом контуре реактора на быстрых нейтронах, достигает 5-9 Ки/кг. При использовании в качестве теплоносителя воды основная доля собственной активности теплоносителя приходится на нуклид 16N. Он имеет период полураспада 7,11 с и испускает γ-кванты с энергией 6,13 МэВ при квантовом выходе 76 %. Кроме него образуются нуклиды 13N и 18F, но они не оказывают существенного влияния на радиационную обстановку первого контура.
Когда теплоноситель омывает внутренние поверхности оборудования первого контура, в него поступают продукты коррозии материалов первого контура. Теплоносителем они проносятся через активную зону и становятся радиоактивными. Вместе с другими примесями они откладываются на внутренних стенках оборудования первого контура. Часть их вновь смывается теплоносителем, часть распадается, часть удаляется фильтрами внутриконтурной водоочистки, но взамен происходит постоянное пополнение теплоносителя свежими продуктами коррозии и, таким образом, со временем наступает равновесное состояние. Продукты коррозии содержат много различных компонентов, поскольку оборудование первого контура изготавливается из высококачественных легированных сплавов, и в результате различных ядерных реакций, происходящих в активной зоне, образуется множество разнообразных радиоактивных нуклидов. Самые распространённые из них:
59Fe – образуются из нерадиоактивных атомов 58Fe и имеют период полураспада 45,1 суток;
56Mn– образуются из 55Mn и имеют период полураспада 2,58 часа;
54Mn – образуются из 54Fe и имеют период полураспада 312,3 суток;
51Cr – образуются из 50Cr и имеют период полураспада 27,73 суток;
58 Со – образуются из 58Ni и имеют период полураспада 70,78 суток;
60Со – образуются из 60Ni и имеют период полураспада 5,272 лет;
95Zr – образуются из 94Zr и имеют период полураспада 64,05 суток.
Кроме них могут образовываться радионуклиды меди, цинка, сурьмы, серебра и другие. Все эти металлы существуют в теплоносителе в виде окислов, поступая туда с продуктами коррозии.
Результаты расчётов парциальных активностей различных изотопов в активной зоне ядерных реакторов и их зависимости от времени представлены в справочнике [7].
В начальный период эксплуатации АЭС суммарная активность теплоносителя, продуктов коррозии и отложений быстро растёт, затем рост замедляется за счёт того, что короткоживущие нуклиды приходят в равновесное состояние и дальнейший рост происходит только за счёт дальнейшего накопления долгоживущих нуклидов. Но постепенно и здесь наступает близкое к равновесному состояние.
Date: 2021-06-08; view: 2516; Нарушение авторских прав
§

Гамма-излучение характеризуют интенсивностью, под которой понимают произведение энергии γ-квантов на их число, падающее ежесекундно на единицу поверхности, нормальной к потоку гамма-квантов.
Как и для любого вида электромагнитного излучения интенсивность γ-излучения точечного источника убывает обратно пропорционально квадрату расстояния от источника излучения (если не происходит его дополнительного поглощения в среде). Это определяется чисто геометрическими свойствами потока излучения, т.е. его расхождением по мере удаления от точечного источника излучения. Реально такое ослабление будет наблюдаться в абсолютном вакууме.
Гамма-излучение относится к сильнопроникающим излучениям. Но при прохождении через любое вещество будет происходить его поглощение этим веществом. Это поглощение может происходить благодаря взаимодействию γ-излучения с атомами, электронами и ядрами вещества, проявляющемуся в виде следующих эффектов [2, 3, 5]:
· фотоэффекта – состоящего в выбивании γ-квантом электронов из внутренних электронных оболочек атомов (чаще всего из К-оболочки), что приводит к его ионизации и появлению свободного электрона. Этот эффект преобладает при энергии γ-квантов ниже 0,5 МэВ;
· эффекта Комптона, который состоит в том, что γ-квант возбуждает электрон во внешней оболочке атома, передавая ему часть своей энергии, в результате чего уменьшается его энергия и изменяется направление (комптоновское рассеяние);
· образования пар – если γ-квант пролетает непосредственно вблизи ядра и при этом его энергия превышает 1,022 МэВ, то может образоваться электрон-позитронная пара;
· фотоядерных реакций, при которых гамма-кванты, поглощаясь ядром, возбуждают его, передавая ему свою энергию, и если эта энергия больше энергии связи нейтрона, протона или альфа-частицы, то эти частицы могут покидать ядро. На делящихся ядрах (235U, 239Pu и др.), если энергия гамма-кванта больше порога деления ядра, будет происходить его деление.
Вследствие всех этих взаимодействий при прохождении гамма-излучения через поглотитель его интенсивность уменьшается по закону [3]:
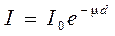 , (3.1)
, (3.1)
где I0 , I – интенсивность γ-излучения до и после прохождения через поглотитель;
μ – линейный коэффициент ослабления;
d – толщина поглотителя.
На рис. 3.1 представлена простая схема эксперимента по ослаблению. Когда гамма-излучение с интенсивностью I0 падает на поглотитель толщиной d, интенсивность I излучения, прошедшего через поглотитель, описывается экспоненциальным выражением (3.1).
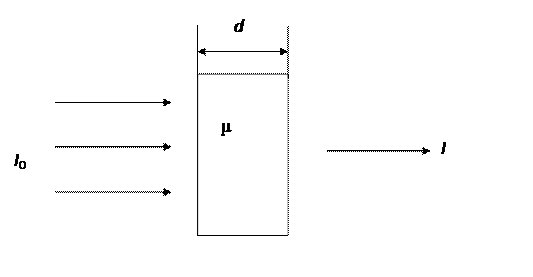
Рис. 3.1. Основной закон ослабления гамма-излучения
Интенсивность прошедшего излучения I является функцией энергии гамма-излучения, состава и толщины поглотителя. Отношение I/I0 называется коэффициентом пропускания гамма-излучения. На рисунке 3.2 [16] показано экспоненциальное ослабление для трёх различных энергий гамма-излучений. Из рисунка видно, что коэффициент пропускания возрастает с увеличением энергии гамма-излучения и снижается с увеличением толщины поглотителя. Коэффициент μ в уравнении (3.1) называется линейным коэффициентом ослабления.

 Линейный коэффициент ослабления μ зависит от энергии γ-квантов и свойств поглощающего материала. Он имеет размерность м-1 и численно равен доле моноэнергетических гамма-квантов, выбывающих из параллельного пучка на единице пути излучения в веществе. Линейный коэффициент ослабления зависит от плотности и порядкового номера вещества, а также от энергии гамма-квантов. Например, свинец обладает высокой плотностью и большим атомным номером и пропускает гораздо меньшую долю падающего гамма-излучения, чем алюминий или сталь такой же толщины.
Линейный коэффициент ослабления μ зависит от энергии γ-квантов и свойств поглощающего материала. Он имеет размерность м-1 и численно равен доле моноэнергетических гамма-квантов, выбывающих из параллельного пучка на единице пути излучения в веществе. Линейный коэффициент ослабления зависит от плотности и порядкового номера вещества, а также от энергии гамма-квантов. Например, свинец обладает высокой плотностью и большим атомным номером и пропускает гораздо меньшую долю падающего гамма-излучения, чем алюминий или сталь такой же толщины.
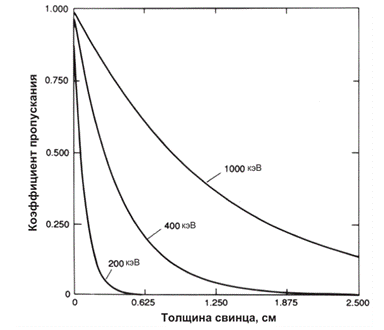
Рис. 3.2. Зависимость коэффициента пропускания гамма-квантов от толщины свинцового поглотителя
Значения линейного коэффициента ослабления гамма-излучения источника 60Со для различных материалов представлены в таблице 3.1, а их зависимость от энергии γ-квантов – в таблице 3.2 [1].
Толщину слоя поглотителя, необходимую для уменьшения интенсивности излучения в два раза называют полутолщиной d1/2 .
Из закона поглощения (3.1) следует, что полутолщина равна
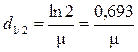 . (3.2)
. (3.2)
Таблица 3.1
Линейный коэффициент ослабления μ материалов γ-излучения Со-60
| Материал | Свинец | Сталь | Чугун | Бетон | Кирпич |
| ρ, кг/дм3 | 11,34 | 7,7 | 7,4 | 3,2-2,1 | 1,7-1,5 |
| μ, см-1 | 0,53 | 0,34 | 0,3 | 0,14-0,09 | 0,075-0,065 |
Таблица 3.2
Зависимость линейного коэффициента ослабления μ материалов
от энергии γ-квантов
| Е, МэВ | μ, см-1 | |||||
| Свинец | Вода | Алюминий | Железо | Графит | Воздух | |
| 0,10 | 0,171 | 0,455 | 2,91 | 0,342 | 2,00·10-4 | |
| 0,15 | 22,8 | 0,151 | 0,371 | 1,55 | 0,304 | 1,76·10-4 |
| 0,20 | 11,1 | 0,137 | 0,328 | 1,15 | 0,277 | 1,59·10-4 |
| 0,30 | 4,43 | 0,119 | 0,280 | 0,865 | 0,241 | 1,38·10-4 |
| 0,40 | 2,62 | 0,106 | 0,249 | 0,740 | 0,214 | 1,23·10-4 |
| 0,50 | 1,80 | 0,0966 | 0,227 | 0,661 | 0,196 | 1,12·10-4 |
| 0,80 | 0,999 | 0,0786 | 0,184 | 0,526 | 0,159 | 9,13·10-5 |
| 1,0 | 0,798 | 0,0279 | 0,165 | 0,471 | 0,143 | 8,21·10-5 |
| 1,5 | 0,591 | 0,0575 | 0,135 | 0,382 | 0,117 | 6,68·10-5 |
| 2,0 | 0,518 | 0,0493 | 0,116 | 0,334 | 0,0999 | 5,74·10-5 |
| 3,0 | 0,475 | 0,0396 | 0,0950 | 0,284 | 0,0801 | 4,63·10-5 |
| 4,0 | 0,472 | 0,0340 | 0,0834 | 0,260 | 0,0684 | 3,98·10-5 |
| 5,0 | 0,480 | 0,0302 | 0,0761 | 0,247 | 0,0603 | 3,54·10-5 |
| 8,0 | 0,519 | 0,0242 | 0,0651 | 0,233 | 0,0482 | 2,87·10-5 |
| 0,552 | 0,0220 | 0,0619 | 0,233 | 0,0439 | 2,62·10-5 | |
| 0,628 | 0,0193 | 0,0584 | 0,241 | 0,0380 | 2,31·10-5 | |
| 0,694 | 0,0180 | 0,0578 | 0,250 | 0,0351 | 2,19·10-5 | |
| 0,792 | 0,0170 | 0,0584 | 0,269 | 0,0329 | 2,08·10-5 | |
| 0,863 | 0,0166 | 0,0603 | 0,285 | 0,0320 | 2,06·10-5 | |
| 0,915 | 0,0166 | 0,0616 | 0,299 | 0,0320 | 2,08·10-5 |
Линейный коэффициент ослабления представляет собой простейший коэффициент ослабления, который можно измерить экспериментально, но он обычно не приводится в справочных таблицах ввиду зависимости от плотности поглощающего материала. Например, вода, лед и пар имеют различные линейные коэффициенты ослабления для одной и той же энергии, хотя они состоят из одного и того же вещества.
Гамма-кванты взаимодействуют, в основном, с атомными электронами, следовательно, коэффициент ослабления должен быть пропорционален плотности электронов P, которая пропорциональна объёмной плотности поглощающего материала. Для любого конкретного вещества отношение плотности электронов к объёмной плотности этого вещества является константой Z/A, независимой от объёмной плотности. Отношение Z/A является почти постояным для всех элементов, кроме самых тяжелых элементов и водорода [16]:
P=Z ρ /A, (3.3)
где P — плотность электронов;
Z — атомный номер;
ρ — массовая плотность;
A — массовое число.
Если поделить линейный коэффициент ослабления на плотность вещества ρ, то получится массовый коэффициент ослабления, не зависящий от плотности вещества [2]:
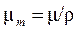 . (3.4)
. (3.4)
Массовый коэффициент ослабления измеряется в см2/г (в системе СИ – м2/кг) и зависит только от порядкового номера вещества и энергии гамма-квантов. Судя по единице измерения этого коэффициента, можно рассматривать его как эффективное сечение взаимодействия электронов на единицу массы поглотителя. Массовый коэффициент ослабления может быть записан через сечение реакции σ (см2):
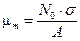 , (3.5)
, (3.5)
где N0 — число Авогадро (6,02  1023);
1023);
А — массовое число поглощающего элемента.
Сечение взаимодействия σiпо своему определению аналогичны сечениям реакции, т.е. определяет вероятность протекания i-го процесса при взаимодействии гамма-кванта с атомом. Оно связано с линейными коэффициентами ослабления μiформулой
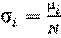 , (3.6)
, (3.6)
где N – количество атомов вещества в 1 см3;
i – краткое обозначение фотоэффекта (ф), комптон-эффекта (к) и эффекта образования пар электрон-позитрон (п).
Сечения выражаются в барнах на атом.
Используя массовый коэффициент ослабления, уравнение (3.1) можно представить следующим образом [16]:
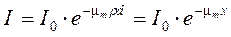 , (3.7) где x = ρd.
, (3.7) где x = ρd.
Массовый коэффициент ослабления не зависит от плотности, а зависит от энергии фотонов и атомного номера поглотителя. На рисунках 3.3 и 3.4 показана зависимость 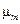 от энергии фотонов в диапазоне от 0.01 до 100 МэВ для групп элементов от углерода до свинца [14]. Этот коэффициент чаще приводится в таблицах, чем линейный коэффициент ослабления, поскольку он количественно определяет вероятность взаимодействия гамма-квантов с конкретным элементом.
от энергии фотонов в диапазоне от 0.01 до 100 МэВ для групп элементов от углерода до свинца [14]. Этот коэффициент чаще приводится в таблицах, чем линейный коэффициент ослабления, поскольку он количественно определяет вероятность взаимодействия гамма-квантов с конкретным элементом.
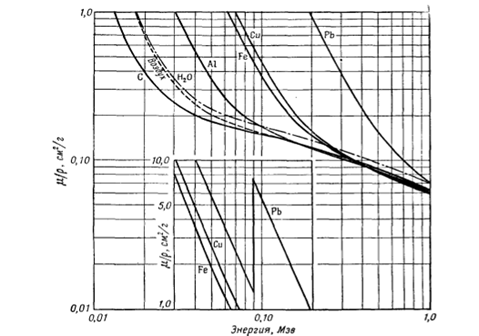
Рис. 3.3. Зависимость полного массового коэффициента поглощения от энергии фотонов для различных материалов (диапазон энергии от 0,01 до 1 МэВ)
|

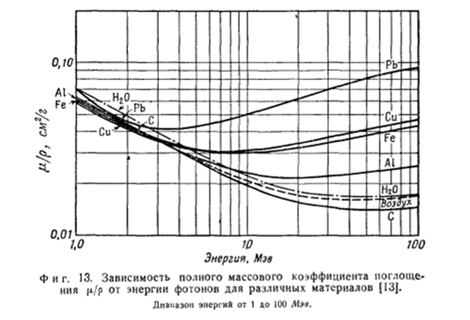
В справочнике [3] приведены таблицы зависимостей линейного и массового коэффициентов ослабления и длины свободного пробега гамма-квантов от их энергии в диапазоне от 0,01 до 10 МэВ для различных веществ.
Взаимодействие гамма-излучения со сложным веществом характеризуется эффективным порядковым номером Zэфф этого вещества. Он равен порядковому номеру такого условного простого вещества, массовый коэффициент ослабления которого при любой энергии гамма-квантов совпадает с массовым коэффициентом ослабления данного сложного вещества. Его рассчитывают из соотношения [2]:
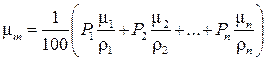 , (3.8)
, (3.8)
где Р1, Р2, …, Рn – весовое процентное содержание составляющих веществ в сложном веществе;
μ1/ρ1 , μ2/ρ2 , …, μn/ρn – массовые коэффициенты ослабления составляющих веществ в сложном веществе.
С учётом названных выше трёх основных эффектов взаимодействия гамма-излучения с веществом полный линейный коэффициент ослабления будет состоять из трёх составляющих, определяемых фотоэффектом, комптон-эффектом и эффектом порождения пар:
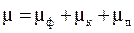 . (3.9)
. (3.9)
Каждый из них различным образом зависит от порядкового номера вещества и энергии гамма-квантов.
При фотоэффектегамма-квант поглощается атомом, а из атома вырывается электрон (рисунок 3.5).
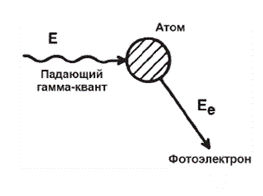
Рис. 3.5. Схема процесса фотоэлектрического поглощения
Часть энергии гамма-кванта, равная энергии связи εе , расходуется на отрыв электрона от атома, а остальная часть преобразуется в кинетическую энергию этого электрона Ее:
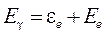 . (3.10)
. (3.10)
Первая особенность фотоэффекта заключается в том, что он протекает только тогда, когда энергия гамма-кванта больше энергии связи электрона в соответствующей оболочке атома. Если энергия гамма-кванта меньше энергии связи электрона в К-оболочке, но больше, чем в L-оболочке, то фотоэффект может идти на всех оболочках атома, кроме К-оболочки, и т.д.
Вторая особенность состоит в увеличении фотоэлектрического поглощения гамма-квантов с ростом энергии связи электронов в атоме. На слабо связанных электронах фотоэффект практически не наблюдается, а свободные электроны вообще не поглощают гамма-кванты. Линейный коэффициент ослабления фотоэффекта пропорционален отношению Z4/Eγ3.
Эта пропорциональность является лишь приблизительной, поскольку показатель степени Z изменяется в диапазоне от 4,0 до 4,8. С уменьшением энергии гамма-кванта вероятность фотоэлектрического поглощения быстро растет (см. рис. 3.6) [16]. Фотоэлектрическое поглощение является преобладающим процессом взаимодействия для гамма-квантов низких энергий, рентгеновских квантов и тормозного излучения.
Фотоэффект в основном наблюдается на K– и L-оболочках тяжёлых атомов при энергиях гамма-квантов до 10 МэВ. Коэффициент μф резко уменьшается с увеличением энергии гамма-квантов и при энергии около 10 МэВ приближается к нулю, т.е. фотоэлектроны не возникают. На рис. 3.6 представлен фотоэлектрический массовый коэффициент ослабления для свинца. Вероятность взаимодействия быстро возрастает с уменьшением энергии, но затем резко снижается при энергии гамма-кванта чуть ниже энергии связи K-электрона. Этот скачок называется K-краем. Ниже этой энергии гамма-квант не имеет достаточно энергии, чтобы выбить K-электрон. Ниже K-края вероятность взаимодействия снова возрастает до тех пор, пока энергия становится ниже энергий связи L-электронов. Такие скачки называются LI– , LII– , LIII– – краями.
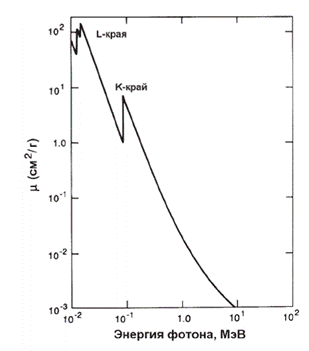
Рис. 3.6. Фотоэлектрический массовый коэффициент ослабления для свинца
На слабо связанных электронах атомов происходит рассеяние γ-квантов, называемое комптон-эффектом. При таком взаимодействии происходят как бы упругие столкновения γ-квантов с эквивалентной массой mγ = E/c2 с электронами массой me. Схематически такое столкновение представлено на рисунке 3.7. В каждом таком столкновении γ-квант передаёт часть своей энергии электрону, придавая ему кинетическую энергию. Поэтому такие электроны называют электронами отдачи. Кинетическая энергия электрона отдачи будет равна
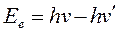 , (3.11)
, (3.11)
где v и 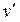 – частота γ-кванта до и после столкновения;
– частота γ-кванта до и после столкновения;
h – постоянная Планка.
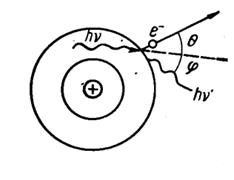
Рис. 3.7. Схема взаимодействия гамма-кванта с веществом
при Комптон-эффекте
После столкновения электрон отдачи и γ-квант разлетаются под углами θ и φ относительно первоначального направления движения γ-кванта. Учитывая законы сохранения энергии и импульса (количества движения), произойдёт изменение длины волны γ-кванта:
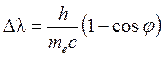 . (3.12)
. (3.12)
При касательных столкновениях γ-квант отклоняется на малые углы (φ ~ 0) и его длина волны изменяется незначительно. Максимальным оно будет при лобовых столкновениях (φ ~ 1800), достигая величины
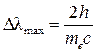 . (3.13)
. (3.13)
Энергия рассеянного гамма-кванта 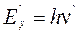 и электрона отдачи Ee связаны с начальной энергией гамма-кванта, с углами φ и θ соотношениями [2]:
и электрона отдачи Ee связаны с начальной энергией гамма-кванта, с углами φ и θ соотношениями [2]:
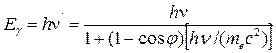 , (3.14)
, (3.14)
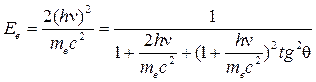 . (3.15)
. (3.15)
Так как взаимодействие γ-кванта с любым электроном независимо, то величина μк пропорциональна плотности электронов Ne , которая, в свою очередь, пропорциональна порядковому номеру Z вещества. Зависимость μк от энергии γ-кванта hv и Z, полученная физиками Клейном, Нишиной и Таммом, имеет вид [3]:
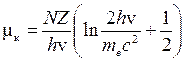 , (3.16)
, (3.16)
где N – число атомов в 1 см3 вещества.
Комптон-эффект идёт главным образом на слабосвязанных электронах внешних оболочек атомов. С увеличением энергии доля рассеянных γ-квантов уменьшается. Но убывание линейного коэффициента рассеяния μкпроисходит медленнее, чем μф. Поэтому в области энергий Eγ > 0,5 МэВ комптон-эффект преобладает над фотоэффектом.
В спектрометрии гамма-излучения используется величина dμк/dEe, называемая дифференциальным коэффициентом комптоновского рассеяния γ-квантов. Его физический смысл состоит в том, что он определяет количество электронов отдачи в единице объёма вещества, образуемое потоком гамма-квантов Ф с энергией Еγ, энергия которых заключена в интервале от нуля до максимального значения Еемакс. Теория Клейна-Нишины-Тамма позволяет получить аналитическое выражение для величины dμк /dEe = Nd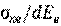 , где N – число атомов в единице объёма вещества. Для иллюстрации этой зависимости приведём графические распределения электронов отдачи для трёх фиксированных энергий гамма-квантов (рис. 3.8) [3]. В случае высоких энергий γ-квантов (более 2 МэВ) распределение электронов отдачи по энергии практически постоянно. Отклонение от постоянного значения (увеличение плотности распределения электронов отдачи) начинается при приближении их энергии к энергии γ-кванта, образуя так называемый комптоновский пик. При этом энергия электронов отдачи в комптоновском пике несколько ниже энергии породивших их гамма-квантов (что и видно из рисунка).
, где N – число атомов в единице объёма вещества. Для иллюстрации этой зависимости приведём графические распределения электронов отдачи для трёх фиксированных энергий гамма-квантов (рис. 3.8) [3]. В случае высоких энергий γ-квантов (более 2 МэВ) распределение электронов отдачи по энергии практически постоянно. Отклонение от постоянного значения (увеличение плотности распределения электронов отдачи) начинается при приближении их энергии к энергии γ-кванта, образуя так называемый комптоновский пик. При этом энергия электронов отдачи в комптоновском пике несколько ниже энергии породивших их гамма-квантов (что и видно из рисунка).
Рис. 3.8. Энергетическое распределение электронов отдачи
для γ-квантов различных энергий
Поскольку выше начальной энергии γ-квантов энергия электронов отдачи быть не может, после комптоновского пика распределение резко обрывается к нулю. При уменьшении энергии γ-квантов (менее 1,5 МэВ) равномерность распределения ниже комптоновского пика также нарушается. На рисунке 3.9 представлена зависимость энергии комптоновского края от энергии гамма-квантов. Из него следует, что с ростом энергии гамма-квантов различие в энергиях фотопика и комптоновского края сначала быстро растёт, но, начиная с энергий 100-200 кэВ это различие стремится к постоянной величине.
Эффект образования парпроисходит при прохождении γ-кванта вблизи ядра, если его энергия превышает пороговое значение 1,022 МэВ. Вне поля ядра γ-квант не может образовать пару электрон-позитрон, т.к. в этом случае будет нарушен закон сохранения импульса. Хотя энергии в 1,022 МэВ достаточно, чтобы породить пару, но тогда импульс порождённых частиц должен быть равен нулю, тогда как γ-квант имеет импульс отличный от нуля и равный Eγ/c. Однако, в поле ядра этот эффект становится возможным, поскольку в этом случае энергия и импульс γ-кванта распределяются между электроном, позитроном и ядром без нарушения законов сохранения. При этом, поскольку масса ядра в тысячи раз превышает массу электрона и позитрона, то оно получает ничтожную часть энергии γ-кванта, которая практически полностью распределяется между электроном и позитроном. Схематично эффект рождения пары электрон-позитрон представлен на рисунке 3.10.
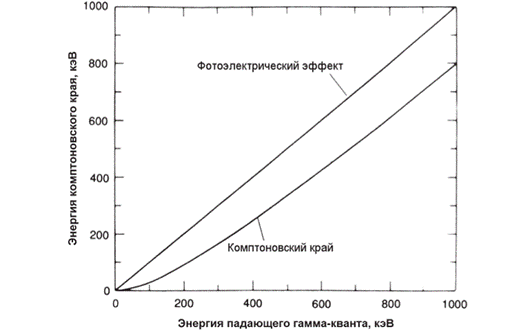
Рис. 3.9. Зависимость энергии комптоновского края от энергии гамма-кванта
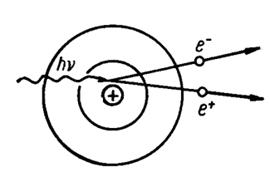
Рис. 3.10. Схема взаимодействия гамма-кванта с веществом
при эффекте образования пар
При превышении пороговой энергии 1,022 МэВ линейный коэффициент ослабления за счёт эффекта образования пар μп становится отличным от нуля и резко растёт, а при энергиях более 5 МэВ его действие становится определяющим. Это наглядно видно из рисунка 3.11 [3] на котором представлены зависимости линейного коэффициента ослабления гамма-излучения и его составляющих для свинца от энергии γ-квантов.
Рис. 3.11. Зависимость линейных коэффициентов ослабления гамма-излучения от энергии γ-квантов для свинца
Все три процесса взаимодействия, описанные выше, вносят вклад в полный массовый коэффициент ослабления. Относительный вклад трёх процессов взаимодействия зависит от энергии гамма-кванта и атомного номера поглотителя. На рис. 3.12 [16] показан набор кривых массового ослабления, охватывающий широкий диапазон энергий и атомных номеров. Коэффициент ослабления для всех элементов, за исключением водорода, имеет резкий подъём в области низких энергий, который указывает, что в этой области преобладающим процессом взаимодействия является фотоэлектрическое поглощение. Расположение этого подъёма сильно зависит от атомного номера. Выше подъёма в области низких энергий значение массового коэффициента ослабления постепенно снижается, определяя область, в которой преобладающим взаимодействием является комптоновское рассеяние.
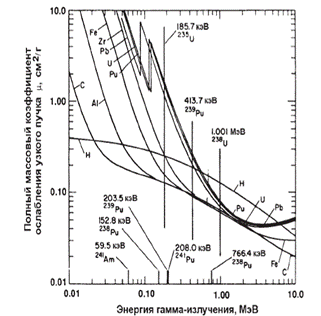
Рис. 3.12. Массовые коэффициенты ослабления некоторых элементов
(показаны энергии гамма-квантов, используемые обычно при
идентификации изотопов урана и плутония по гамма-излучению)
Массовые коэффициенты ослабления для всех элементов с атомным номером меньше, чем 25 (железо), практически идентичны в энергетическом диапазоне от 200 до 2000 кэВ. В диапазоне от 1 до 2 МэВ кривые ослабления сходятся для всех элементов. Форма кривой массового ослабления водорода показывает, что взаимодействие гамма-квантов с энергией больше 10 кэВ проходит почти исключительно путём комптоновского рассеяния. При энергиях выше 2 МэВ для элементов с высоким атомным номером Z важным становится процесс взаимодействия с образованием пар, и массовый коэффициент ослабления снова начинает расти [16].
Date: 2021-06-08; view: 5474; Нарушение авторских прав
§

Лёгкие заряженные частицы – электроны и позитроны – образуются при бета-распаде. Они объединяются в одну группу β-частиц. Электроны и позитроны имеют одинаковые массы и равные по абсолютной величине, но противоположные по знаку заряды. В радиоактивных превращениях β-частицы возникают вместе с нейтрино. При этом энергия распада распределяется между β-частицей и нейтрино. Поэтому β-частицы характеризуются непрерывным энергетическим спектром от нуля до Еmax. Энергия Еmaxпри бета-распаде не превышает 10 МэВ. Большей энергии β-частиц можно достичь, лишь разгоняя электроны в специальных ускорителях или в результате эффекта образования электрон-позитронных пар при облучении атомов тяжёлых веществ высокоэнергичными гамма-квантами.
Процессы замедления электронов и позитронов в веществе идентичны, поэтому далее будут рассматриваться только электроны.
Взаимодействие электронов с веществом характеризуется эффектами, происходящими при взаимодействии электронов с атомами или молекулами вещества поглотителя. Эти взаимодействия электронов с нейтральными атомами и молекулами принято характеризовать упругими и неупругими столкновениями. А вероятности этих столкновений принято характеризовать сечениями. Сечения нельзя отождествлять с поперечным сечением частицы-мишени, поскольку для одной и той же частицы при столкновениях, приводящих к различным последствиям, его величина различна. Она зависит от свойств соударяющихся частиц, законов их взаимодействия и скорости относительного движения электрона и соударяющейся частицы.
Сечения упругих столкновений электронов с нейтральными атомами и молекулами зависят от скорости электронов v или энергии ε = mе v2 /2 , где те– масса электрона. Определить сечения расчётным путём весьма сложно, поскольку они определяются действием на электрон силового поля атома или молекулы, а при энергиях электронов в единицы электрон-вольт длина волны электрона сравнима с размерами атомов. Поэтому чаще всего используют экспериментально найденные зависимости сечений упругих столкновений электронов с молекулами вещества от энергии электронов. Примеры таких зависимостей для ряда газов приведены на рисунке 3.13 [17].
Как видно из этих рисунков, зависимости сечений упругих столкновений электронов с молекулами различных газов от энергии электронов существенно различны. Следует отметить, что вследствие огромной разницы в массах электрона и молекул газа потери энергии электронов при упругих столкновениях с ними очень малы и составляют весьма малую долю начальной энергии (менее 10-4). Поэтому, чтобы отдать свою энергию молекулам газа электрон должен испытать более 10000 столкновений. При этом сечения упругих столкновений электронов с атомами и молекулами газа существенно (в десятки раз) превосходят сечения неупругих столкновений даже в том диапазоне энергий электронов, который достаточен для совершения неупругого столкновения. Ниже этого энергетического порога неупругие столкновения вообще невозможны.
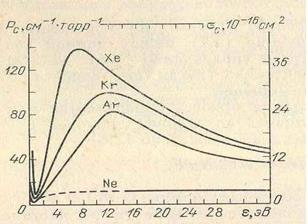
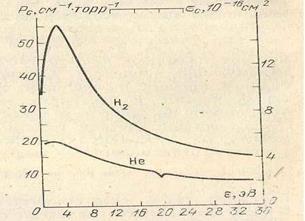
Рис. 3.13. Вероятности и сечения упругих столкновений электронов
с атомами некоторых газов в зависимости от энергии электронов
Неупругими называют столкновения, в результате которых происходит превращение одной или обеих сталкивающихся частиц в другие частицы или изменение их внутренней энергии (за счёт возбуждения электронных оболочек атомов или молекул, участвующих в столкновении).
При столкновениях с атомными электронами происходит либо их выбивание из атома – ионизация атома, либо их перевод на более высокую орбиту. Поскольку такое возбуждённое состояние атома является неустойчивым, то электрон испускает избыточную энергию в виде электромагнитного кванта и возвращается в исходное состояние. Кроме того, при столкновениях с молекулярными газами может происходить возбуждение молекулярных колебаний в них и диссоциация молекул газа.
Ионизация нейтральных атомов или молекул при электронном ударе может произойти лишь в том случае, когда энергия электрона достаточна для вырывания электрона из электронной оболочки атома или молекулы. При этом ударяющий электрон затрачивает энергию, равную энергии связи вырываемого электрона с атомом или молекулой. Естественно, что для разных атомов и молекул она различна. Эту энергию называют потенциалом ионизации I. Но для окончательного отрыва электрона нужно придать ему ещё достаточную кинетическую энергию. Поэтому экспериментально измеренные пороговые энергии ионизации εи почти вдвое превышают потенциалы ионизации. Особый интерес представляют начальные участки этих зависимостей, где энергия электронов незначительно превышает потенциал ионизации. Вблизи этого порога эти зависимости можно аппроксимировать прямой
σi = Ci (ε – I), ε ≥ I . (3.17)
Здесь коэффициент пропорциональности Сi, определяющий наклон этой прямой, называют наклоном сечений ионизации.
Однако даже когда энергия электрона превосходит потенциал ионизации, вероятность акта ионизации при столкновении с нейтральным атомом или молекулой остаётся существенно меньшей, чем вероятность упругого столкновения. Это отражается существенно меньшими значениями сечений ионизации по сравнению с сечениями упругих столкновений. На рисунке 3.14 приведены экспериментально измеренные зависимости сечений ионизации для некоторых газов от энергии ударяющих электронов, а в таблице 3.3 [17] – потенциалы ионизаций I, пороговые энергии ионизации εи и коэффициенты Ci для ряда газов.
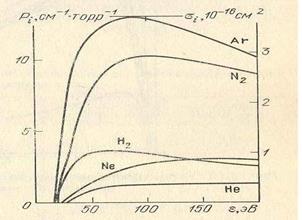
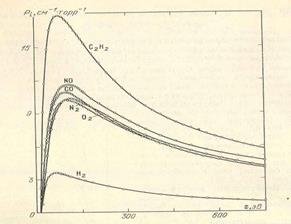
Рис. 3.14. Вероятности и сечения ионизации некоторых газов
электронными ударами в широком диапазоне энергий электронов
Таблица 3.3
Потенциалы и экспериментальные энергии ионизации
и наклоны сечений ионизации некоторых газов
| Газ | He | Ne | Ar | N2 | O2 | H2 | CO2 | Воздух |
| I,эВ | 24,6 | 21,6 | 15,8 | 15,6 | 12,2 | 15,4 | 13,8 | – |
| εи ,эВ | 42,3 | 36,6 | 26,4 | 34,7 | 30,9 | 36,3 | 32,8 | 33,9 |
| Сi ∙10–20м2/эВ | 1,3 | 1,6 | 8,5 | 6,8 | 5,9 | 0,68 | – |
Поскольку β-излучение обладает непрерывным энергетическим спектром, характеризуемым максвелловским распределением, то коэффициенты ионизации определяют для средних сечений ионизации 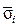 , которые численно примерно равны Сi (
, которые численно примерно равны Сi ( 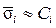 ), если Сiвыразить в м2 /эВ. Таким образом, значения Сi, представленные в таблице 3.3, примерно соответствуют средним сечениям ионизации
), если Сiвыразить в м2 /эВ. Таким образом, значения Сi, представленные в таблице 3.3, примерно соответствуют средним сечениям ионизации 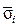 . Потенциалы ионизации возбуждённых атомов и молекул несколько ниже, чем у невозбуждённых (ровно на ту энергию, которая требуется для их возбуждения и которая лежит в пределах единиц электрон-вольт). Это означает, что такую ступенчатую ионизацию могут совершать более медленные электроны, энергия которых ниже потенциала ионизации. При этом многие газы имеют по нескольку метастабильных состояний, характеризующихся различными энергиями возбуждения и временем жизни. Следовательно, даже если средняя энергия электронов ниже потенциала ионизации, то ионизация всё равно происходит, только менее интенсивно, во-первых, за счёт того, что в соответствии с максвелловским распределением энергии электронов среди них всегда есть электроны с энергией, превосходящей среднюю и достигающие потенциала ионизации, а во-вторых, за счёт ступенчатой ионизации возможна ионизация и более медленными электронами.
. Потенциалы ионизации возбуждённых атомов и молекул несколько ниже, чем у невозбуждённых (ровно на ту энергию, которая требуется для их возбуждения и которая лежит в пределах единиц электрон-вольт). Это означает, что такую ступенчатую ионизацию могут совершать более медленные электроны, энергия которых ниже потенциала ионизации. При этом многие газы имеют по нескольку метастабильных состояний, характеризующихся различными энергиями возбуждения и временем жизни. Следовательно, даже если средняя энергия электронов ниже потенциала ионизации, то ионизация всё равно происходит, только менее интенсивно, во-первых, за счёт того, что в соответствии с максвелловским распределением энергии электронов среди них всегда есть электроны с энергией, превосходящей среднюю и достигающие потенциала ионизации, а во-вторых, за счёт ступенчатой ионизации возможна ионизация и более медленными электронами.
Следует также иметь в виду, что по мере роста энергии электронов (свыше потенциала ионизации) вероятность ионизации частиц при электронных ударах растёт лишь до определённых пределов, а при дальнейшем возрастании энергии электронов (свыше 100-200 эВ) начинает убывать (см. рис. 3.14). Это очень важный вывод, поскольку говорит о том, что существует оптимальный диапазон энергий электронов, при котором вероятность ионизирующих столкновений будет максимальна и для каждого газа этот оптимальный диапазон энергий различен. И ниже, и выше этого оптимального диапазона вероятность ионизирующих электронных ударов будет уменьшаться.
Пробег частиц в веществе можно исследовать путём снятия кривых поглощения (рисунок 3.15) [14]. На нём приведены кривые поглощения для коллимированного пучка моноэнергетических электронов и для бета-частиц с непрерывным энергетическим спектром.
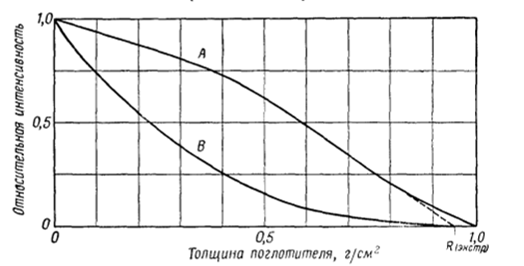
|
Большинство частиц испытывает рассеяние и выходит из пучка. Только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности.
Кривая поглощения моноэнергетических электронов имеет линейный участок. Если линейный участок экстраполировать до оси абсцисс, как это сделано на рисунке 3.16, то такое экстраполированное значение пробега может служить характеристикой частицы с данной энергией. Полученную таким образом величину считают обычно пробегом электрона.
Для электронов с непрерывным энергетическим спектром пробег совершенно невозможно определить из кривых, подобных кривым на рисунке 3.16. Однако разработаны методы, при помощи которых можно из данных по поглощению рассчитать пробег электрона. Один из таких методов, известный под названием метода сравнения Физера [14], позволяет определить пробег в каком-либо вещества путём сравнения кривой поглощения в этом веществе с кривой поглощения в веществе с известным пробегом.
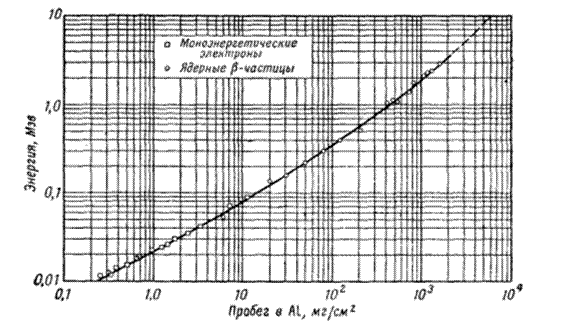
Рис. 3.16. Зависимость пробега электронов от энергии
На рисунке 3.16 представлены результаты Гленденина [14]. Эти результаты описываются следующими эмпирическими формулами:
R = 0,542E – 0,133, 0,8 < E < 3 МэВ;
R = 0,407E1.38, 0,15 < E < 0,8 МэВ , (3.18)
где R – пробег в г/см2;
Е – энергия электрона в МэВ.
Значительная часть кривой поглощения бета-излучения, испускаемого при радиоактивном распаде (см. кривая В на рис. 3.15), описывается экспоненциальной зависимостью.
В жидкостях и твёрдом веществе атомы и молекулы располагаются друг от друга на значительно меньших расстояниях, чем в газах. Поэтому поглощение β-излучения в жидкостях и твёрдых веществах происходит в десятки и сотни раз интенсивней, чем в газах. При этом и для газов, и для жидкостей, и для твёрдых веществ может быть использован тот же закон поглощения, что и для γ-излучения (3.1), но показатель экспоненты μd удобнее выражать через массовый коэффициент ослабления μm= μ/ρ, учитывающий плотность поглотителя ρ:
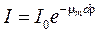 , (3.19)
, (3.19)
где d – толщина слоя поглотителя.
Действительно, при подстановке значений μm мы приходим к форме (3.1):
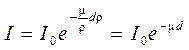 .
.
Массовый коэффициент ослабления μmзависит от энергии β-частиц. Но, поскольку энергия любого источника β-частиц неоднородна, то обычно используют максимальную энергию Emax. Зависимость μmот Emax с хорошим приближением отображается эмпирической формулой [3]
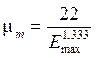 . (3.20)
. (3.20)
Учитывая идентичность законов поглощения для всех видов излучения, для β-излучения также вводят понятие слоя половинного ослабления – полутолщины:
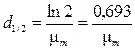 . (3.21)
. (3.21)
Однако ввиду того, что 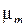 зависит от энергии β-частиц, а их энергетический спектр непрерывен, и при максвелловском распределении средняя энергия электронов будет примерно в три раза меньше максимальной, то, соответственно, усреднённая полутолщина окажется меньше, чем вычисленная по формуле (3.21). Слой половинного ослабления зависит от максимальной энергии спектра электронов Emax и свойств поглощающего вещества. В таблице 3.4 [3] приведены значения μ и d1/2 для пучков электронов с различными значениями Emaxв алюминии.
зависит от энергии β-частиц, а их энергетический спектр непрерывен, и при максвелловском распределении средняя энергия электронов будет примерно в три раза меньше максимальной, то, соответственно, усреднённая полутолщина окажется меньше, чем вычисленная по формуле (3.21). Слой половинного ослабления зависит от максимальной энергии спектра электронов Emax и свойств поглощающего вещества. В таблице 3.4 [3] приведены значения μ и d1/2 для пучков электронов с различными значениями Emaxв алюминии.
Таблица 3.4
Значения μ и d1/2 для пучков электронов с различными
значениями Emaxв алюминии
| Emax , МэВ | μ, см-1 | d1/2 , мг/см2 |
| 0,15 0,50 1,00 2,00 3,00 | 35,1 | 2,7 17,5 |
Как видим, зависимость весьма сильная: при увеличении максимальной энергии бета-излучения в 20 раз линейный коэффициент ослабления уменьшается почти в 78 раз, и во столько же раз возрастает слой половинного ослабления.
Аналогичен характер этих зависимостей и для других материалов.
Date: 2021-06-08; view: 1850; Нарушение авторских прав
§

Альфа-частицы относят к тяжёлым частицам (наряду с протонами, нейтронами, дейтронами и тритонами). Собственно, α-частицы представляют собой ядра атомов гелия и состоят из двух протонов и двух нейтронов, т.е. имеют атомную массу 4 и заряд 2. В этой группе частиц массы различаются не более чем в 4 раза, а заряды – в 2 раза. Поэтому могут быть установлены точные соотношения между величинами пробегов, линейными коэффициентами ослабления и другими характеристиками взаимодействия этих частиц с веществом. Поэтому достаточно рассмотреть взаимодействие с веществом альфа-частиц, а для остальных тяжёлых заряженных частиц существуют пересчётные формулы для определения характеристик их взаимодействия с веществом, учитывающие различие их масс и зарядов по сравнению с альфа-частицами.
Известно большое число радиоактивных изотопов, при распаде которых образуются α-частицы. Их энергия зависит от того, каким радиоактивным веществом они испускаются, и не превышает 9 МэВ. Более высокие энергии альфа-частиц (до десятков гигаэлектрон-вольт) могут быть получены в ускорителях заряженных частиц..
Двигаясь в веществе, α-частицы испытывают электрические взаимодействия с электронами атомов, в процессе которых постепенно теряют свою энергию, после чего, присоединяя к себе электроны, нейтрализуются, образуя атомы гелия. Атомные электроны, получив от α-частицы во время столкновения порцию энергии, либо вырываются из атома, либо переходят на более высокую орбиту, т.е. α-частица вдоль своей траектории движения производит ионизацию и возбуждение атомов вещества. При этом число возбуждённых атомов в несколько раз превышает число ионизированных.
При полном замедлении α-частицы суммарная потеря энергии на ионизацию Е1 и возбуждение Е2 атомов равна начальной кинетической энергии α-частицы:
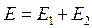 . (3.22)
. (3.22)
Если в процессе замедления α-частицы возникло N ионных пар, то средняя энергия, затрачиваемая α-частицей в веществе на образование одной ионной пары, будет равна
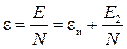 . (3.23)
. (3.23)
Величину ε называют энергией образования ионной пары. Она больше энергии ионизации атома εи = Е1/N примерно в два раза. Чтобы найти число ионных пар, возникающих при полном торможении частицы в веществе, необходимо кинетическую энергию α-частицы разделить на соответствующее значение ε. В таблице 3.5 [3] представлены значения энергии образования ионной пары и энергии ионизации для некоторых чистых газов.
Таблица 3.5
Энергия образования ионной пары ε и энергия ионизации εи
некоторых чистых газов
| Газ | ε, эВ | εи , эВ | Газ | ε, эВ | εи , эВ | |
| He Ne Ar Kr Xe H2 CO2 | 42,7 36,8 26,4 24,1 21,9 36,3 34,5 | 24,56 21,56 15,76 14,00 12,13 15,43 13,73 | O2 N2 CH4 C2H2 C2H6 C2H4 Воздух | 32,5 36,6 29,2 27,5 26,6 28,0 35.5 | 12,20 15,51 13,04 11,35 11,76 10,51 – |
При небольших энергиях α-частицы начинается её «перезарядка». Сравнительно медленно пролетая рядом с электроном, она может захватить его, в результате чего её заряд уменьшается на единицу. Однако в последующих столкновениях, она вновь теряет его. В результате таких перезарядок ионизация атомов возрастает, а сама частица быстрее тормозится. Зависимость изменения удельной ионизации от пройденного в веществе пути ионизирующей частицей иллюстрируется кривой Брэгга, представленной на рисунке 3.17-а, а зависимость плотности потока от пройденного в веществе пути – на рисунке 3.17-б [3].
Пик на кривой Брэгга объясняется особенностями взаимодействия медленных α-частиц с атомными электронами. Чем медленнее движется α-частица, тем больше время её взаимодействия с атомными электронам, а следовательно, и вероятность ионизации атома. Но когда начинается процесс перезарядки, α-частица резко тормозится, её энергия падает и вероятность ионизации также резко падает. Затем α-частица, исчерпав свою энергию, останавливается и нейтрализуется. Поскольку масса α-частицы в тысячи раз больше массы электронов, то при столкновениях с электронами она практически не отклоняется от направления своего первоначального движения и её траектория представляет собой прямую линию. Расстояние, проходимое α-частицей от источника до остановки, называют линейным пробегом R.

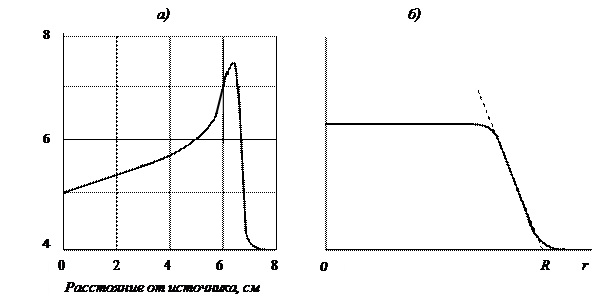

Рис. 3.17. Изменение удельной ионизации при торможении α-частицы
в воздухе (кривая Брэгга) – а, и зависимость потока α-частиц от расстояния до источника – б (R – экстраполированный пробег, R0 – средний пробег)
Некоторый разброс в пробегах моноэнергетических α-частиц объясняется вероятностным характером их взаимодействия с электронами атомов. Частицы теряют свою энергию в большом, но конечном числе актов столкновений. Флуктуациям подвержено как число таких актов на единицу пути, так и потери энергии в каждом акте. Поэтому за величину линейного пробега принимают либо средний пробег R0 , либо экстраполированный линейный пробег R, который близок к максимальному пробегу (см. рис. 3.17-б). Разница между экстраполированным и средним пробегами называется разбросом пробегов: δ = R – R0. Величина разброса составляет примерно 1 % от экстраполированного пробега при энергии α-частиц 5 МэВ.
Альфа-излучение обладает существенно более сильным ионизирующим действием, чем β-излучение, вследствие существенно большей массы и энергии α-частиц. Поэтому глубина проникновения альфа-излучения в вещество существенно меньше.
Глубиной проникновения считается толщина слоя поглотителя, при прохождении через который интенсивность излучения ослабляется в е раз.
Она также зависит от энергии α-частиц и для воздуха при температуре 15 0С и давлении 101,3 кПа её можно подсчитать по эмпирической формуле [3]:
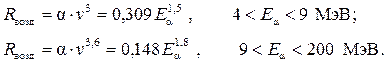 (3.24)
(3.24)
где глубина проникновения R определяется в см, а энергия Е – в МэВ.
При энергии α-частиц в 10 МэВ глубина проникновения в воздухе составляет около 10 см. В твёрдых веществах глубина проникновения α-излучения составляет доли или единицы мм.
Соотношение между пробегом и энергией α-частиц в различных веществах широко изучалось как теоретически, так и экспериментально. С хорошей точностью пробег α-частиц в веществе с атомным номером А можно рассчитать по эмпирической формуле [14]
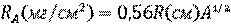 , (3.25)
, (3.25)
где R – пробег α-частиц в воздухе при температуре 150 С и давлении 760 мм рт. ст. (101,3 кПа), который находится по формулам (3.24).
Пробег частиц в различных веществах можно выразить через пробег в воздухе при помощи так называемой относительной тормозной способности. Она представляет собой отношение тормозной способности данного вещества к тормозной способности воздуха.
Тормозная способность выражается либо в виде потери энергии частицы на единице пути – линейная тормозная способность, либо в виде потери энергии частицы на единице толщины, выраженную через массу, приходящуюся на единицу площади – массовая тормозная способность.
Абсолютные тормозные способности для любого вещества очень сильно зависят и от вида частиц и от их энергии. Использование относительной тормозной способности позволяет в значительной степени ослабить зависимости от вида и энергии частиц. Это видно и из приведенной ниже таблицы 3.6 [14], где приведены относительные тормозные способности (линейная SL и массовая Sm) нескольких металлов для α-частиц различной энергии и пробег тех же частиц в воздухе.
Таблица 3.6
Относительные тормозные способности некоторых материалов
для α-частиц различных энергий
| Энергия частицы. МэВ | Пробег в воздухе, см | Al, ρ = 2,7 г/см3 | Cu, ρ = 8,9 г/см3 | Pb, ρ = 11,0 г/см3 | |||
| SL | Sm | SL | Sm | SL | Sm | ||
| 2,0 | 0,80 | – | – | 0,32 | |||
| 6,3 | 0,79 | 0,58 | 0,33 | ||||
| 9,7 | 0,81 | 0,59 | 0,35 | ||||
| 0,86 | 0,65 | 0,39 |
Из неё следует, что если пробег α-частиц в воздухе (а значит и абсолютная линейная тормозная способность воздуха) при изменении энергии α-частиц от 2 МэВ до 37 МэВ изменяется в 100 раз, то относительные тормозные способности для указанных материалов (особенно массовая) при том же диапазоне изменения энергии α-частиц изменяются всего в пределах 10 процентов. Таким образом, относительную тормозную способность удобно использовать именно как характеристику вещества при взаимодействии с ионизирующими излучениями.
Если известно соотношение между пробегом и потерями энергии для данного вида частиц в данном веществе, то можно получить расчётным путём соответствующее соотношение для другого типа частиц в том же веществе. Для этого можно воспользоваться аналитическим выражением тормозной способности материала, определяющим потери энергии частицей на единице пути dE/dx в данном материале:
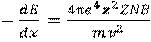 , (3.26)
, (3.26)
где Е – кинетическая энергия частицы;
z – её заряд;
v – её начальная скорость;
N – число атомов в 1 см3 поглотителя;
Z – атомный номер поглотителя;
B – коэффициент торможения;
е – заряд электрона;
m – масса электрона.
Для частицы массой М и зарядом z, используя (3.19), можно найти расстояние, пройденное в данном веществе, на котором её энергия изменится от начальной энергии Е до нуля :
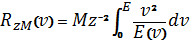 , (3.27)
, (3.27)
С помощью уравнения (3.27) можно найти пробег протонов Rp(v) с начальной скоростью v через пробег α-частиц в том же веществе с той же начальной скоростью:
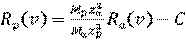 . (3.28)
. (3.28)
Постоянная С здесь введена для учёта процесса захвата и потери электронов (процесса «перезарядки») при малых энергиях. Это связано с тем, что протоны и α-частицы имеют различные заряды, а потому различным образом взаимодействуют с атомными электронами. Экспериментально было найдено, что величина С для воздуха при нормальных температуре и давлении для энергий больших 0,5 МэВ равна 0,20 см. С уменьшением энергии величина С плавно уменьшается и при 6,7 кэВ достигает величины 0,02 см.
Таким образом, для воздуха и для энергий больших 0,5 МэВ можно записать
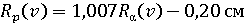 , (3.29)
, (3.29)
а т.к. при равных скоростях частиц для их энергий справедливо соотношение
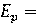 EαMp /Mα , то вместо (3.29) можно записать
EαMp /Mα , то вместо (3.29) можно записать
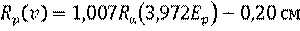 . (3.30)
. (3.30)
Здесь 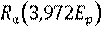 означает пробег α-частицы, рассчитанный для энергии, равной 3,972 от соответствующей энергии протона.
означает пробег α-частицы, рассчитанный для энергии, равной 3,972 от соответствующей энергии протона.
Если нужно найти пробег частицы с таким же зарядом, но с другой массой (например, дейтронов или тритонов по отношению к протонам), то поправочный коэффициент С в выражении (3.28) исчезает, т.к. процесс захвата и потери атомарных электронов у этих частиц протекает одинаково. Поэтому, если известен пробег частицы массой М0 в веществе, то рассчитать пробег в этом веществе другой частицы с таким же зарядом, но другой массой М, можно по формуле
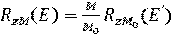 , (3.31)
, (3.31)
где 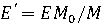 .
.
Date: 2021-06-08; view: 1710; Нарушение авторских прав
§

Нейтрон (англ. neutron, от лат. neuter, символ n), нейтральная (не обладающая электрическим зарядом) элементарная частица со спином 1/2 (в единицах постоянной Планка h) и массой mn = 1,008665 а.е.м., что незначительно превышает массу протона. Из протонов и нейтронов построены все атомные ядра. Нейтроны были открыты в 1932 г. английским физиком Дж. Чедвиком, который установил, что обнаруженное немецкими физиками В. Боте и Г. Бекером проникающее излучение, возникающее при бомбардировке атомных ядер (в частности, бериллия) a-частицами, состоит из незаряженных частиц с массой, близкой к массе протона.
Нейтроны устойчивы только в составе стабильных атомных ядер. Свободный нейтрон — нестабильная частица, распадающаяся на протон, электрон е– и электронное антинейтрино 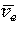 [3, 5, 9]:
[3, 5, 9]:
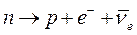 . (3.32)
. (3.32)
Период полураспада нейтрона равен 11,7 мин. Среднее время жизни свободного нейтрона t » 16 мин. В веществе свободные нейтроны существуют ещё меньше (в плотных веществах: единицы-сотни микросекунд) вследствие их сильного поглощения ядрами. Поэтому свободные нейтроны возникают в природе или получаются в лаборатории только в результате ядерных реакций. В свою очередь, свободный нейтрон способен взаимодействовать с атомными ядрами, вплоть до самых тяжёлых. Исчезая, нейтрон вызывает ту или иную ядерную реакцию, из которых особое значение имеет деление тяжёлых ядер, а также радиационный захват нейтронов, приводящий в большинстве случаев к образованию радиоактивных изотопов.
Как и другие ядерные частицы, нейтрон обладает корпускулярными и волновыми свойствами. Длина волны моноэнергетического нейтронного излучения определяется:
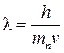 , (3.33)
, (3.33)
где h – постоянная Планка;
mn – масса нейтрона;
v – его скорость.
Волновые свойства нейтрона проявляются при малых энергиях. С ростом скорости нейтронов длина волны уменьшается и при больших скоростях волновые свойства перестают влиять на взаимодействия нейтронов с веществом.
Большая эффективность нейтронов в осуществлении ядерных реакций, своеобразие взаимодействия с веществом медленных нейтронов (резонансные эффекты, дифракционное рассеяние в кристаллах и т.п.) делают нейтроны исключительно важным орудием исследования в ядерной физике и физике твёрдого тела. Имеется много важных практических приложений, где нейтроны играют ключевую роль: ядерная энергетика, производство трансурановых элементов и радиоактивных изотопов (искусственная радиоактивность). Нейтроны широко используются в химическом анализе (активационный анализ) и в геологической разведке (нейтронный каротаж).
В зависимости от энергии нейтронов принята следующая их условная классификация: ультрахолодные нейтроны (с энергией менее 10-7 эВ), очень холодные (10-7-10-4 эВ), холодные (10-4-5×10-3 эВ), тепловые (5×10-3-0,5 эВ), резонансные (0,5-104эВ), промежуточные (104-105 эВ), быстрые (105-108эВ), высокоэнергичные (108-1010 эВ) и релятивистские (³ 1010 эВ). Все нейтроны с энергией до 105 эВ объединяют общим названием медленные нейтроны [1-3, 5]. Часто все нейтроны с энергией между тепловыми и быстрыми (от 0,5 эВ до 0,1 МэВ) относят к промежуточным, считая резонансные нейтроны частью промежуточных.
Источниками нейтронного излучения могут служить радиоизотопные источники с (α, n)-реакцией, фотонейтронные источники, использующие реакцию (γ, n), мишени из различных веществ, бомбардируемые заряженными частицами (протонами, дейтронами, α-частицами и др.), разогнанными до высоких энергий на ускорителях заряженных частиц, а также делящиеся вещества, в процессе спонтанного деления ядер которых вылетают нейтроны. Более подробно все они были рассмотрены в предыдущем разделе.
Но наиболее мощным источником нейтронов является ядерный реактор, в котором плотности потоков нейтронов в активной зоне достигают 1014 нейтрон/(см2·с). При этом их энергия лежит в диапазоне 0,1…20 МэВ. Взаимодействуя с замедлителем и конструкционными материалами реактора, они замедляются, и их энергетический спектр расширяется вплоть до тепловых энергий.
Вследствие своей электрической нейтральности для нейтронов существенно лишь взаимодействие с ядрами атомов. При этих взаимодействиях нейтроны в зависимости от их энергии могут вступать в различные процессы: упругое и неупругое рассеяние, захват нейтрона с последующим излучением фотонов (радиационный захват), захват с испусканием заряженных частиц, деление ядер. Сечения указанных процессов являются сложными функциями от энергии нейтронов и специфичны для ядер различных элементов и даже для изотопов одного и того же элемента.
Ввиду того, что процессы взаимодействия нейтронов с ядрами различных веществ носят сложный характер и специфичны для различных веществ, зависимости сечений этих взаимодействий от энергии нейтронов и характеристик ядра мишени не удаётся выразить аналитически. Поэтому соответствующие экспериментально измеренные зависимости для различных ядер представлены в виде таблиц или графиков [7-8, 10, 18-19]. В частности, такие данные представлены в многотомном атласе BNL-325, который периодически переиздаётся по мере накопления новых данных. В последнее время такие данные принято хранить в электронном виде, а поскольку данные, полученные различными авторами, нередко существенно разнятся, то в ряде стран создают библиотеки так называемых «оценённых» данных, которые рекомендованы к применению в различных расчётах. В России это библиотека БРОНД, в Великобритании – UKNDL, в США – ENDF/B, в Германии – KEDAK и т.д.
Следует отметить некоторые отличия соотношения интенсивности различных нейтронных процессов для лёгких и тяжёлых ядер. Для лёгких и средних ядер при любых энергиях нейтронов преобладает упругое рассеяние. Резонансное рассеяние для лёгких ядер существенно при больших энергиях нейтронов E > 100 кэВ, а для средних – при 1 кэВ < E < 100 кэВ. Для тяжёлых ядер для тепловых и надтепловых нейтронов доминирует радиационный захват, а затем, по мере возрастания энергии – поочерёдно: упругое, резонансное и неупругое рассеяние. Процесс ослабления нейтронного излучения при прохождении через вещество складывается из процессов замедления быстрых и промежуточных нейтронов (неупругое и упругое рассеяние), диффузии и захвата тепловых нейтронов. Соответственно, нейтронная защита выполняется из смеси (слоёв) тяжёлых элементов (железо, свинец), обеспечивающих неупругое рассеяние нейтронов, лёгких водород- и углеродсодержащих веществ (вода, парафин, графит), в которых происходит упругое рассеяние нейтронов, и элементов захвата тепловых нейтронов (водород, бор). При среднем соотношении 1:4 тяжелых и лёгких элементов ослабление потока нейтронов в 10:100:1000 раз достигается в слоях примерно 20:32:40 см. Из всех видов внешних воздействий на человека нейтронное излучение наиболее опасно, т.к. интенсивно замедляется и поглощается водородсодержащей средой организма и вызывает ядерные реакции в его внутренних органах, приводящие к появлению радиоактивных изотопов с различными периодами полураспада, т.е. к накоплению внутренней радиоактивности.
Существует много типов взаимодействия нейтрона с ядром. На рисунке 3.18 [16] показаны типы взаимодействий нейтронов и их сечения. На этом рисунке каждый тип взаимодействия состоит из всех взаимодействий, которые находятся ниже и соединены с ним. Взаимодействие может быть одним из двух основных типов: рассеянием или поглощением. Когда нейтрон рассеивается на ядре, его скорость и направление изменяются, но ядро остаётся с тем же самым числом протонов и нейтронов, которое оно имело до взаимодействия. Ядро может перейти в возбужденное состояние, что приведет в конечном итоге к испусканию излучения. Если нейтрон поглощается ядром, то может испускаться широкий спектр излучения или произойти деление ядра.
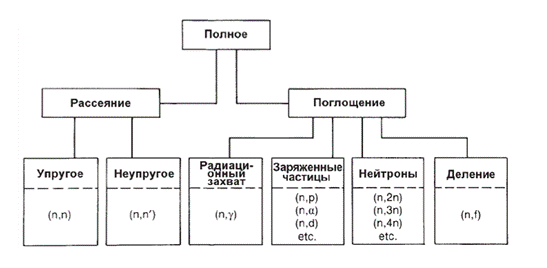 Рис. 3.18. Классификация типов нейтронных взаимодействий (буквы, разделенные запятыми в скобках, показывают вызывающие реакцию
Рис. 3.18. Классификация типов нейтронных взаимодействий (буквы, разделенные запятыми в скобках, показывают вызывающие реакцию
и образующиеся частицы)
В ядерных реакциях, являющихся источниками нейтронов, образуются, как правило, быстрые нейтроны (с энергией от 1 до 20 МэВ). При соударениях с атомными ядрами окружающего вещества они теряют энергию за счёт различных взаимодействий с ними: – упругого рассеяния; неупругого рассеяния; ядерных реакций.
При упругом рассеянии нейтрон расходует энергию на сообщение ядру скорости без изменения его внутреннего состояния. При одном лобовом упругом соударении нейтрон теряет в среднем долю энергии, равную 2А/(А 1)2, где А — массовое число ядра-мишени. Из данного выражения следует, что чем больше масса ядра, тем меньшую долю энергии теряет нейтрон при упругом столкновении с ним. Для тяжёлых ядер эта доля мала (1/100 для свинца), для лёгких ядер велика (1/7 для углерода и 1/2 для водорода). Это понятно, поскольку та же закономерность наблюдается и при упругих соударениях макротел. Поэтому замедление нейтронов происходит на лёгких ядрах гораздо быстрее, чем на тяжёлых. Именно поэтому в ядерных реакторах на тепловых нейтронах в качестве замедлителей используют лёгкие элементы (воду – эффективным замедлителем являются ядра атомов водорода; тяжёлую воду, где используется тяжёлый изотоп водорода – дейтерий; графит, в котором замедлителем являются ядра атомов углерода). Сечение упругого рассеяния обратно пропорционально скорости нейтрона. Поэтому при прохождении через тяжёлые и средние вещества упругое рассеяние вносит малую долю в общие потери их энергии.
Таблица 3.7
Среднее число столкновений, необходимое для снижения энергии нейтрона от 2 МэВ до 0,025 МэВ в результате упругого рассеяния 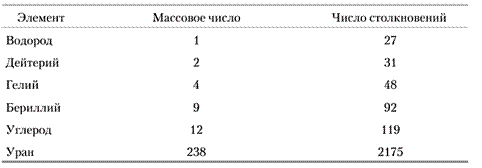
Неупругое рассеяние заключается в том, что при столкновении с ядром нейтрон не только передаёт ему часть своей кинетической энергии (как при упругом столкновении), но и изменяет его потенциальную энергию, т.е. возбуждает его. При этом он, конечно, расходует больше энергии, чем при упругом столкновении. Неупругое рассеяние является возможным, когда энергия нейтронов больше энергии первого возбуждённого состояния ядра-мишени (десятки и сотни килоэлектронвольт). Поэтому при энергиях нейтронов порядка от нескольких мегаэлектронвольт до десятков килоэлектронвольт главную роль в потерях энергии при их прохождении через вещества со средними и большими атомными весами играют неупругое и упругое рассеяния нейтронов.
Однако, чем выше энергия нейтронов, тем более вероятными становятся ядерные реакции (за некоторыми исключениями, которые, как мы увидим дальше, как раз и используются для детектирования медленных нейтронов). При ядерных реакциях нейтроны теряют энергию крупными порциями, расходуя её главным образом на возбуждение ядер или их расщепление. Ядерные реакции записывают в виде: A(a, bcd)B,где А — ядро мишени, а — бомбардирующая частица, в, с, d — испускаемые частицы, В — остаточное ядро (в скобках записываются более лёгкие продукты реакции, вне — наиболее тяжёлые). Ядерные реакции подчиняются законам сохранения электрического заряда, числа нуклонов, энергии и импульса. Закон сохранения числа нуклонов означает сохранение массового числа А. Ядерные реакции могут протекать с выделением и с поглощением энергии Q, которая в 106 раз превышает энергию, поглощаемую или выделяемую при реакциях химических.Поэтому в ядерных реакциях можно заметить изменение масс взаимодействующих ядер. Энергия Q, выделяемая или поглощаемая при ядерных реакциях, равна разности сумм масс частиц (в энергетических единицах) до и после ядерной реакции в соответствии с теорией относительности.
Ядерные реакции под действием нейтронов в большинстве случаев протекают с поглощением энергии Q. Они могут быть различных типов [18]:
– с выделением протонов (п, р);
– с выделением альфа-частиц (п, α);
– с выделением двух и более частиц, например, реакция (п, 2п);
– реакции деления тяжёлых ядер.
Последние занимают особое место, поскольку сопровождаются выделением большого количества энергии. Именно на этих реакциях основана современная ядерная энергетика. В то же время для некоторых ядер (например, 238U) реакция деления имеет энергетический порог, связанный с необходимостью преодоления потенциального барьера деления (нейтроны должны иметь достаточно большую энергию, чтобы преодолеть его). Поэтому с 238U могут вступать в реакцию только быстрые нейтроны и её конечным продуктом является радиоактивный изотоп 239Pu. Такая реакция и имеет место в реакторах на быстрых нейтронах. Деление под действием медленных нейтронов (с энергией менее 0,1 МэВ) испытывают ядра 235U, 242Am, 245Cm, 249Cf. Из них для энергетики используется только реакция с 235U. Ядерные реакции деления являются самоподдерживающимися только в том случае, когда вместе с продуктами деления из ядра вылетают нейтроны. Такие реакции называют цепными. Веществ, в которых под действием нейтронов могут происходить цепные ядерные реакции немного и все они достаточно редкие. Именно это ограничивает сырьевую базу современной ядерной энергетики. Практически это только уран.
Однако ядерные реакции с выделением двух и более нейтронов могут происходить практически со всеми веществами, но они не сопровождаются выделением энергии, а, напротив, поглощают энергию, равную энергии, необходимой для отделения нейтрона от ядра, например для указанной ядерной реакции (n, 2n) она равна ~10 МэВ. Поэтому при энергиях нейтронов выше 10 МэВ, преобладающую роль играют ядерные реакции типа (n, 2n).
При ядерных реакциях деления и реакциях (n, 2n) высокоэнергичный нейтрон поглощается ядром и вместо него вылетают два и более нейтронов с существенно меньшей энергией. (Именно поэтому цепные реакции могут возникать только в тех веществах, в которых деление ядер происходит при столкновениях с медленными нейтронами). Таким образом, можно считать, что при прохождении быстрых нейтронов через вещества с большими и средними атомными весами они, благодаря ядерным реакциям деления и нейтронного размножения, теряют энергию крупными порциями и превращаются в медленные нейтроны.
Для медленных нейтронов основной процесс дальнейшей потери энергии — радиационный захват нейтрона, т.е. ядерные реакции типа (n, g). Исключение составляют 3He и 14N, для которых основной процесс — ядерные реакции (п, р) а также 6Li и 10B, для которых преобладает ядерная реакция (n, α). У средних и тяжёлых ядер потенциальный барьер препятствует вылету протонов и a-частиц. Область энергий медленных нейтронов (0,5 эВ-0,1 МэВ) является резонансной. В этой области энергий наблюдается наличие так называемых нейтронных резонансов – резкого увеличения (в 10-105 раз) поглощения и рассеяния нейтронов определённых энергий. Образующееся после захвата нейтрона высоковозбуждённое состояние ядра нестабильно (время жизни ~10-15 с): ядро распадается с испусканием нейтрона (резонансное рассеяние нейтронов) или g-кванта (радиационный захват). Значительно реже испускаются a-частица или протон. Для некоторых очень тяжёлых ядер (U, Pu и др.) происходит также деление возбуждённого ядра на 2, реже на 3 осколка.
Максимальная вероятность резонансного захвата для большинства ядер соответствует энергии в несколько эВ. При более высоких энергиях для большинства ядер эффективное сечение захвата обратно пропорционально скорости нейтронов (закон 1/v).
Как уже говорилось выше, при резонансном захвате нейтрона образующееся возбуждённое ядро может распадаться не только с выделением гамма-кванта (радиационный захват), но и вступать в ядерные реакции типа (n, p) и (n, a). При ядерных реакциях типа (n, p) для большинства ядер поглощаемая энергия Q невелика (исключение составляют 3H и 14N, для которых реакция протекает с выделением энергии). Для ядерных реакций типа (п, α) в случае лёгких ядер поглощаемая энергия Q также невелика (исключение составляют 6Li и 10B, для которых реакция также протекает с выделением энергии), а при реакциях со средними и тяжёлыми ядрами выделяется небольшое количество энергии. Именно названные исключения и используются для детектирования нейтронов, поскольку выделяющиеся при этом заряженные частицы (протоны и альфа-частицы) легко детектируются обычными методами.
В результате одного или ряда столкновений (в зависимости от их типа) энергия нейтрона становится меньше минимальной энергии возбуждения ядра и ядерные реакции прекращаются. Дальнейшие потери энергии нейтронов (их замедление) могут происходить только в результате упругих столкновений. Замедление нейтронов в принципе должно происходить до тех пор, пока не установится термодинамическое равновесие с окружающим веществом, что приводит, в конечном счёте, к образованию так называемых тепловых нейтронов — газа нейтронов, находящегося в тепловом равновесии со средой, в которой происходит замедление нейтронов. Средняя энергия тепловых нейтронов при комнатной температуре равна 0,04 эВ. Однако, в силу того, что свободные нейтроны – неустойчивые частицы и, диффундируя в веществе, после ряда упругих столкновений с ядрами этого вещества при каком-то очередном столкновении будут обязательно поглощены этим ядром, большинство нейтронов не успевает достичь теплового равновесия. Поэтому средняя энергия тепловых нейтронов всегда выше теоретически равновесной и составляет примерно 0,05 эВ.
В процессе замедления часть нейтронов теряется, поглощаясь при столкновении с ядрами или вылетая из среды наружу. В замедлителях нейтронов – веществах, содержащих лёгкие ядра, слабо захватывающие нейтроны, – при достаточно больших размерах замедлителя потери малы и большая часть нейтронов, испущенных источником, превращается в тепловые нейтроны (для этого размеры замедлителя должны быть велики по сравнению с размером LБ области, в которой нейтроны диффундируют за время замедления). При небольших размерах (меньших средней длины пролёта нейтронов данной энергии в данной среде) большая часть нейтронов в результате рассеяния вылетает за пределы замедлителя.
К числу лучших замедлителей, широко используемых в ядерной физике и ядерной технике для превращения быстрых нейтронов в тепловые, относятся вода, тяжёлая вода, бериллий, графит (таблица 3.8) [19]. При упругих столкновениях с ядрами любого вещества (твёрдого, жидкого или газообразного) нейтроны ведут себя так же, как нейтральные атомы в газе, т.е. подчиняются обычным законам диффузии.
Таблица 3.8
Среднее число столкновений N, среднее время замедления t и
среднее квадратичное удаление LБ нейтрона от источника при замедлении нейтрона в неограниченной среде от энергии 1 МэВ до энергии 0,1 эВ
| Вещество | N | t. мксек | LБ, см |
| Свинец | |||
| Графит | |||
| Вода |
Таким образом, прохождение нейтронов через вещество, сопровождается многократным изменением направления и скорости их движения в результате столкновений с атомными ядрами. Более энергичные нейтроны, т. е. нейтроны с энергией, во много раз большей, чем средняя энергия теплового движения частиц среды, отдают энергию среде и замедляются. В неограниченной среде тепловые нейтроны, обмениваясь энергией с ядрами атомов окружающей среды и между собой, диффундируют до тех пор, пока не поглотятся одним из атомных ядер.
Для вычисления ослабления плотности направленных потоков нейтронов при прохождении их через различные вещества водится понятие макроскопического поперечного сечения Σ, определяющего ослабление нейтронного потока при прохождении через данное вещество. Его называют эффективным сечением и определяют как [9]
Σ = σN , (3.34)
где σ – эффективное микроскопическое (квантово-механическое) сечение взаимодействия нейтрона с ядром атома мишени;
N – число ядер в 1 см3 вещества.
В свою очередь, эффективное микроскопическое сечение σ складывается из трёх составляющих: сечения упругого рассеяния σs , сечения неупругого рассеяния σs’, сечения радиационного захвата σr и сечения ядерных реакций σа , для каждой из возможных реакций обозначаемое индексом испускаемых в результате реакции ядерных частиц (p, n, α, γ и т.д.):
σa = σr σp σα … . Соответственно, полное (эффективное) сечение, обозначаемое σ или σtбудет состоять из: σ = σt = σs σs` σa .
Определение эффективных сечений для ряда возможных ядерных реакций представляют собой сложную задачу. В большинстве случаев эти сечения сильно зависят от энергии нейтронов. Кроме того, они могут иметь совершенно различные значения для разных элементов и для разных изотопов одного и того же элемента. Эффективные сечения, как правило, определяют экспериментально. Исчерпывающий перечень эффективных сечений для тепловых нейтронов и кривые зависимости сечений от энергии для широкого энергетического интервала содержится в работе [19].
Заметим, что, как правило, сечение взаимодействия уменьшается с увеличением энергии. При низких значениях энергии, ниже 1 эВ, сечение упругого рассеяния приблизительно постоянно, тогда как сечение поглощения нейтрона обратно пропорционально скорости нейтрона, т.е. 1/v. Поэтому при низких энергиях полное сечение взаимодействия может быть приблизительно постоянным или может уменьшаться с ростом энергии в зависимости от того, какой тип событий является доминирующим. Например, в случае ядра 239Pu преобладает взаимодействие с поглощением нейтронов, поэтому полное сечение взаимодействия уменьшается по закону 1/v. Аналогичное поведение наблюдается для большинства ядер с малыми и промежуточными массовыми числами. На рис. 3.19 и 3.20 [16] показано поведение полного сечения взаимодействия для бора и кадмия при низких энергиях нейтрона. Необычно высокие значения сечений взаимодействия с поглощением нейтрона для этих двух веществ делают их полезными в качестве поглотителей тепловых нейтронов.
На рисунке 3.21 [11] показано полное эффективное сечение водорода. Это сечение в основном обусловлено упругим рассеиванием на протонах – ядрах атомов водорода. Рассеяние на протонах играет очень важную роль при регистрации быстрых нейтронов.
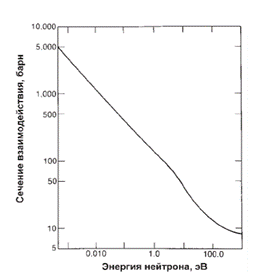
Рис. 3.19. Полное сечение взаимодействия нейтронов с бором в области низких энергий
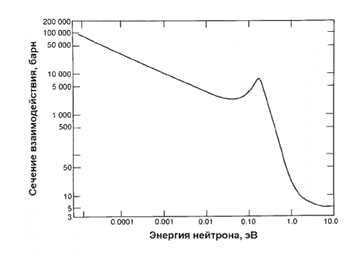
Рис. 3.20. Полное сечение взаимодействия нейтронов с кадмием
в области низких энергий
На рисунке 3.22 [11] изображено полное эффективное сечение естественной смеси изотопов элемента индия.
Величина, обратная макроскопическому эффективному сечению представляет собой длину свободного пробега нейтронов в данном веществе:
λ = 1/Σ . (3.35)
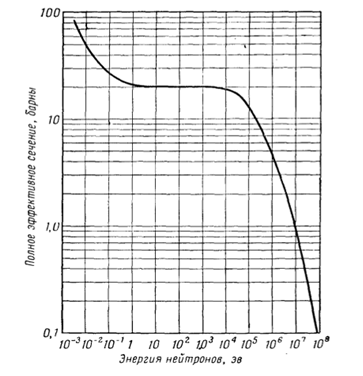
Рис. 3.21. Зависимость полного эффективного сечения водорода от энергии нейтронов
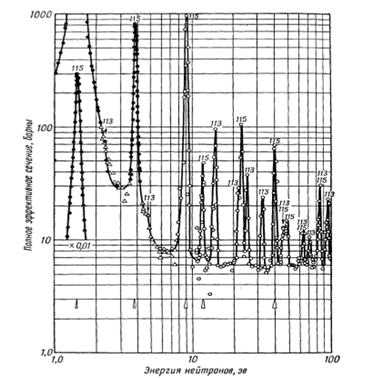
Рис. 3.22. Зависимость полного эффективного сечения индия
от энергии нейтронов
При прохождении быстрых нейтронов через замедляющую среду, состоящую из лёгких элементов, нейтроны преимущественно будут испытывать упругое рассеяние. В этом случае для характеристики этого процесса используется понятие средней длины свободного пробега рассеяния нейтронов
λs = 1/Σs = 1/(Nσs) . (3.36)
На рис. 3.23 [16] показаны несколько траекторий для нейтронов с кинетической энергией 1 МэВ, взаимодействующих с цилиндрами из различных материалов. Средняя длина свободного пробега зависит как от типа материала, так и от энергии нейтрона. После каждого столкновения энергия нейтрона уменьшается и, соответственно, изменяется средняя длина свободного пробега нейтрона. Как видно из рис. 3.26, цилиндр из полиэтилена более эффективно препятствует переносу нейтронов, чем цилиндр из тяжелых металлов. Нейтрон теряет большую часть своей энергии при столкновении с легкими ядрами в полиэтилене, вследствие чего средняя длина свободного пробега нейтрона уменьшается, а сечения взаимодействия увеличиваются. Важное свойство полиэтилена заключается в том, что он накапливает большую часть нейтронов на определенной глубине; эти нейтроны испытали достаточное количество столкновений и потеряли почти всю свою кинетическую энергию. Если детектор тепловых нейтронов помещается в эту область, вероятность обнаружения нейтронов становится оптимальной. В тех случаях, когда ослабление плотности нейтронного потока при прохождении через вещество обусловлено поглощением нейтронов в этом веществе, а процессами рассеяния можно пренебречь, ослабление характеризуют средней длиной релаксации нейтронов в данной среде
λа = 1/Σа = 1/(Nσа) . (3.37)
Длина релаксации – это расстояние, при прохождении которого в данном веществе плотность потока нейтронов вследствие их поглощения уменьшается в е раз, т.е. при х = λа J = J0 /e.
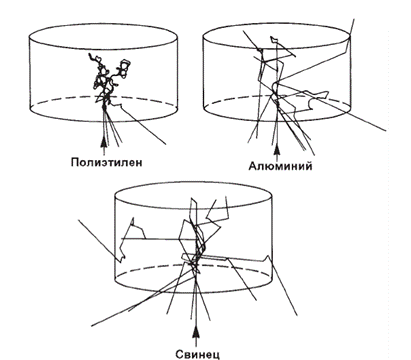
Рис. 3.23. Схема траекторий нейтронов с начальной кинетической
энергией 1 МэВ, входящих в цилиндр вещества снизу и затем
испытавших рассеяние или поглощение (результаты получены
моделированием методом Монте-Карло)
Важной величиной, широко используемой в нейтронной дозиметрии, является средний логарифмический декремент энергии на одно столкновение ξ, которая показывает уменьшение энергии нейтрона (E0 – E1) в результате одного столкновения с ядром вещества [9]
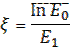 . (3.38)
. (3.38)
При сферически симметричном рассеянии средний логарифмический декремент не зависит от начальной энергии нейтрона и зависит только от массы ядра мишени [9]:
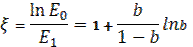 , (3.39)
, (3.39)
где 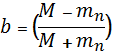 ; (3.40)
; (3.40)
М – атомная масса ядра мишени;
mn – масса нейтрона.
При М/mn > 10 с погрешностью не более 1 % можно использовать приближённую формулу
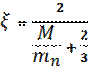 . (3.41)
. (3.41)
Используя формулу (3.38) можно найти среднее число столкновений, необходимое для уменьшения энергии нейтрона от Е0 до Еn:
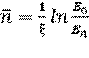 (3.42)
(3.42)
В таблице 3.9 приведены значения 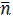 и
и 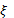 , необходимые для замедления нейтрона от Е0 = 2 МэВ до тепловой энергии Еn= 0,025 эВ.
, необходимые для замедления нейтрона от Е0 = 2 МэВ до тепловой энергии Еn= 0,025 эВ.
Таблица 3.9
Значения 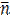 и
и 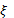 , необходимые для замедления нейтрона от Е0 = 2 МэВ
, необходимые для замедления нейтрона от Е0 = 2 МэВ
до тепловой энергии Еn= 0,025 эВ для разных веществ
| Вещество | М |  | 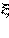 |
| H | 1,000 | ||
| D | 0,725 | ||
| He | 0,425 | ||
| Li | 0,268 | ||
| Be | 0,209 | ||
| C | 0,158 | ||
| N | 0,136 | ||
| O | 0,120 | ||
| Pb | 0,0096 | ||
| U | 0,0084 |
Как следует из формулы (3.41) в качестве замедлителей быстрых нейтронов необходимо использовать вещества с небольшим массовым числом. К ним относятся все водородсодержащие вещества, в том числе и вода. Однако вода и другие водородсодержащие вещества имеют большое сечение захвата тепловых и надтепловых нейтронов, в результате чего при прохождении через неё плотность потока замедленных нейтронов резко падает.
Макроскопическое сечение поглощение нейтронов в веществе, как мы уже видели, характеризуется величиной Σа , поэтому для характеристики замедляющей способности вещества используют коэффициент замедления ξΣs/Σа , который, конечно, также зависит от энергии нейтронов. Если поперечное сечение захвата нейтронов Σамало, то на некотором расстоянии от источника быстрых нейтронов будут накапливаться тепловые нейтроны, которые находятся в тепловом равновесии со средой и далее уже будут распространяться по законам диффузии, пока не будут поглощены атомами среды. Длина пути от точки образования до точки поглощения теплового нейтрона называется длиной диффузии нейтронов Ld . Длину диффузии можно подсчитать по формуле [9]
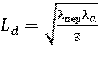 , (3.43)
, (3.43)
где представляет собой среднюю транспортную длину свободного пробега нейтронов с учётом различных углов соударения нейтрона и ядра среды; 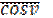 определяется соотношением масс ядра мишени и нейтрона [9]:
определяется соотношением масс ядра мишени и нейтрона [9]:
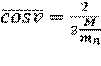 . (3.44)
. (3.44)
Средний квадрат расстояния, проходимый тепловым нейтроном от места своего возникновения до места поглощения, определяется выражением
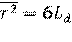 . (3.45)
. (3.45)
Рассматривая в целом процесс замедления быстрых нейтронов в какойлибо среде, вводят понятие длины замедления. Длина замедления Lsхарактеризует среднее расстояние 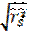 (по прямой), проходимое нейтроном в замедляющей среде с потерей энергии от Е0 до Е:
(по прямой), проходимое нейтроном в замедляющей среде с потерей энергии от Е0 до Е:
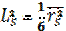 . (3.46)
. (3.46)
Для определённости длиной замедления считают расстояние, проходимое быстрым нейтроном в замедляющей среде с потерей энергии от Е0 (её часто принимают равной 2 МэВ) до тепловой энергии Ет = 0,025 эВ.
В таблице 3.10 представлены характеристики замедляющей способности ряда веществ с небольшими массовыми числами. Из неё следует, что наибольший коэффициент замедления имеют тяжёлая вода (12000) и графит (170), а обычная вода, хотя и имеет большее значение потерь энергии нейтрона на одно столкновение и меньшее значение длины замедления, чем тяжёлая вода, но за счёт существенно большего (почти в тысячу раз) сечения поглощения нейтронов имеет коэффициент замедления только 72.
Таблица 3.10
Характеристики замедляющей способности некоторых веществ для
нейтронов с начальной энергией 2 МэВ
| Вещество | 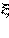 Σs , см-1 Σs , см-1 | Σа ∙102 , см-1 | 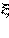 Σs/Σа Σs/Σа | Ls , см |
| Вода | 1,53 | 2,02 | 5,7 | |
| Тяжёлая вода | 0,37 | 2,72∙10-3 | 11,0 | |
| Бериллий | 0,176 | 0,11 | 9,9 | |
| Графит | 0,064 | 3,55∙10-2 | 18,7 |
Для характеристики процесса замедления быстрых нейтронов в среде от момента вхождения в эту среду до момента их поглощения после замедления до тепловой энергии используют понятие длины миграции нейтронов LM. Эта величина связана с длиной замедления и длиной диффузии простым соотношением
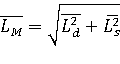 . (3.47)
. (3.47)
В таблице 3.11 приведены диффузионные характеристики веществ, наиболее часто используемых для получения тепловых нейтронов.
Таблица 3.11
Диффузионные характеристики некоторых замедлителей нейтронов
| Вещество | Плотность, г/см3 | Ld , см | λпер , см | λа, см |
| Вода | 1,00 | 2,73 | 0,45 | |
| Тяжёлая вода | 1,1 | 2,40 | ||
| Бериллий | 1,84 | 20,8 | 1,43 | |
| Графит | 1,62 | 50,8 | 2,75 | |
| Парафин | 0,895 | 2,42 | 0,40 |
Date: 2021-06-08; view: 4396; Нарушение авторских прав
§

В предыдущем разделе было показано, что при взаимодействии ионизирующих излучений с веществом могут происходить различные физические эффекты: прямая ионизация атомов за счёт взаимодействия их электронных, оболочек с заряженными частицами, приводящая к появлению электронно-ионных пар; косвенная ионизация атомов при взаимодействии их электронных оболочек с фотонами за счёт фотоэффекта и комптон-эффекта, также приводящее к появлению электронно-ионных пар; рождение свободных зарядов (электрон-позитронных пар) при взаимодействии высокоэнергичных фотонов с ядрами атомов; рождение свободных зарядов (ядер отдачи) при упругом и неупругом взаимодействии нейтронов с ядрами атомов; испускание ядрами атомов заряженных частиц (протонов, альфа-частиц, электронов и позитронов) в результате ядерных реакций при взаимодействии их с нейтронами и высокоэнергичными фотонами; возбуждение атомов (молекул), приводящее к излучению фотонов; нагрев вещества за счёт торможения в нём ядерных частиц и поглощения фотонов. Реже используются химические эффекты (диссоциация молекул, инициация определённых химических реакций) в чувствительном элементе регистрирующей системы – детекторе.
Детектор является главным элементом любой системы, предназначенной для регистрации ионизирующих излучений. Главной функцией детектора является преобразование энергии, выделившейся в результате взаимодействия ионизирующего излучения с активным веществом детектора в сигнал, удобный для регистрации (электрический, визуальный, тепловой). Само активное вещество детектора может находиться в газообразном, жидком и твёрдом состояниях, что определяет специфические особенности процессов взаимодействия с ионизирующими излучениями. С другой стороны, как это следует из предыдущего раздела, эти процессы в сильной степени зависят от вида ионизирующего излучения и его энергии. Даже при регистрации заряженных частиц (альфа- и бета-частиц, протонов, дейтронов и др.) такие важные характеристики их взаимодействия с активным веществом детектора, как проникающая способность и коэффициент поглощения в сильной степени зависят не только от вида частиц, но и от их энергии (скорости). Для фотонного и нейтронного излучений эти зависимости ещё сложнее. Кроме того, в большинстве детекторов даже при измерении излучения определённого вида одновременно могут протекать несколько из указанных эффектов, и каждый из них может вносить определённый вклад в выходной сигнал детектора. И, наконец, любой вид излучения может характеризоваться несколькими параметрами: плотностью излучения (числом частиц или фотонов, приходящих на единицу поверхности, перпендикулярной к направлению их движения, за единицу времени), угловой направленностью, средней и максимальной энергией или распределением числа частиц по энергии (энергетическим спектром), дозовыми характеристиками, временными характеристиками. Все эти характеристики важны для практики и могут являться целью измерений, что существенно влияет на выбор используемых при измерениях физических эффектов и методов измерений, а также накладывает определённые требования на выбор и конструкцию детекторов. Всё это существенно затрудняет классификацию методов регистрации ионизирующих излучений и используемых для этого детекторов. Поэтому общепринятой классификации и методов регистрации, и детекторов ионизирующих излучений ещё не сложилось. В соответствии с используемым физическим эффектом методы регистрации ионизирующих излучений разделяют на:
· ионизационные в газовой среде (газонаполненные ионизационные детекторы: ионизационные камеры, пропорциональные счётчики, счётчики Гейгера-Мюллера,);
· ионизационные в твёрдом веществе (полупроводниковые детекторы: германиевые, кремниевые и др.);
· трековые ионизационные методы с визуальным считыванием (камеры Вильсона и пузырьковые камеры);
· трековые ионизационные методы с электронным считыванием (многопроволочные ионизационные камеры и пропорциональные счётчики, дрейфовые камеры, искровые камеры);
· фотохимические и химические методы (фотоплёнки, рентгеновские плёнки, ядерные эмульсии, твердотельные трековые детекторы);
· сцинтилляционные методы в газовой, жидкой и твёрдой среде (сцинтилляционные газовые, жидкостные и твердотельные детекторы);
· люминесцентные и термолюминесцентные методы (носимые индивидуальные дозиметры);
· метод, использующий излучение Вавилова-Черенкова (черенковские счётчики);
· калориметрический метод (измерение энергии излучения, поглощённой веществом детектора).
По измеряемой (контролируемой) характеристике излучения выделяют радиометрические (дозиметрические) методы и приборы, предназначенные для измерения интегральной плотности излучений (мощности дозы), спектрометрические, предназначенные для измерений энергетического спектра излучений, трековые, предназначенные для визуализации и регистрации траекторий движения ядерных частиц.
В свою очередь, радиометрические методы разделяются по видам регистрируемых излучений и по измеряемой характеристике излучения. По видам измеряемых излучений различают методы регистрации плотности потоков заряженных частиц (альфа-, бета-, протонного и др.), фотонного излучения (гамма- и рентгеновского), нейтронного и других видов излучений. По измеряемой характеристике приборы разделяют на радиометры и дозиметры. Радиометры определяют плотность потока излучения (число частиц или фотонов, падающих за 1 секунду на единицу площади, перпендикулярной направлению потока частиц). Дозиметры определяют дозу или мощность дозы излучения, т.е. отношение энергии переданной излучением элементарному объёму вещества к массе вещества в данном объёме за произвольный отрезок времени (доза) или за единицу времени (мощность дозы). Практически все дозиметры измеряют базисные дозиметрические характеристики, не учитывающие возмущения, вносимые в исходное поле излучения самим объектом, поглощающим излучение. Биологическое же действие излучения на человека или его отдельные органы рассчитывается по специальным методикам по базисным величинам.
Ниже эти методы рассмотрены более подробно.
Date: 2021-06-08; view: 732; Нарушение авторских прав
§

Ионизация газа под воздействием ионизирующих излучений используется для их регистрации весьма широко, поскольку использование этого эффекта позволяет создавать простые по устройству, дешёвые и удобные в эксплуатации детекторы различных видов ионизирующих излучений.
Принцип действия газонаполненных детекторов ионизирующих излучений состоит в следующем. Ядерное излучение, попавшее в объём детектора, представляющего собой герметичный сосуд, наполненный газом, и содержащий, как минимум, два электрода: анод и катод, на которые подаётся постоянное напряжение, создающее в рабочем объёме детектора достаточно сильное электрическое поле, производит в нём первичную ионизацию газа либо непосредственно за счёт потери энергии излучением (в случае детектирования заряженных частиц), либо через вторичные эффекты взаимодействия измеряемого излучения с газовой средой (в случае нейтральных частиц или гамма-квантов). Электроны и ионы, образовавшиеся в результате ионизации газа, движутся в электрическом поле между электродами, создавая тем самым ионизационный ток. При этом происходит собирание и накопление зарядов на электродах, а также «разряд» источника питания через среду рабочего объёма детектора. Свободные электроны при движении в газе испытывают множество соударений с молекулами газа. Среднее расстояние, которое свободный электрон проходит между двумя соударениями, называют средним свободным пробегом. Он обратно пропорционален числу молекул газа в единице объёма. Для большинства используемых в газоразрядных приборах газов при нормальных значениях температуры и давления средний свободный пробег электронов лежит в пределах от 0,5до 3мкм. При отсутствии электрического поля электроны (как и молекулы газа) движутся хаотически. Но в присутствии электрического поля на это хаотичное движение накладывается ещё общий дрейф в направлении, противоположном направлению электрического поля (электроны движутся к положительному электроду – аноду). Средняя скорость этого дрейфа w прямо пропорциональна напряжённости электрического поля Е и обратно пропорциональна давлению газа р:
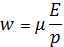 , (4.1)
, (4.1)
здесь коэффициент μ называется подвижностью свободных зарядов и сложным образом зависит от массы носителей зарядов, вида газа, величины электрического поля и давления газа. Для большинства газов подвижность электронов в диапазоне отношений Е/р = 1…10 В/(м∙Па) имеет порядок 104 м/с. При росте отношения Е/р свыше 10 В/(м∙Па) подвижность стремится к максимальному значению, примерно равному 5∙104 -105 м/с. При столкновениях с нейтральными атомами электроны могут присоединяться к их электронным оболочкам, образуя отрицательные ионы. Для галогенов, кислорода и паров воды вероятность присоединения электронов к атомам (образования отрицательных ионов), характеризуемая коэффициентом прилипания [20], примерно равна 10-4, а для таких газов, как водород, аргон, азот, метан – уменьшается до величины 10-6.
В зависимости от режима работы детектора выходной сигнал с него может поступать в непрерывном или дискретном виде. В первом случае интенсивность излучения, попавшего в объём детектора, определяется средней величиной ионного тока (интегральный режим), а во втором случае – числом импульсов в единицу времени (импульсный режим). Выходной сигнал детектора определяется величиной первичной ионизации, т.е. числом первичных пар ионов и свободных электронов, создаваемых в объёме детектора пролетающей через него частицей, а также зависит от характера происходящего в нём газового разряда. В соответствии с характером процесса, обеспечивающего регистрацию излучения, различают: ионизационные камеры, пропорциональные счётчики, счётчики Гейгера-Мюллера.
Ионизационная камера представляет собой систему двух электродов в объёме, заполненном инертным газом (чаще всего аргоном и неоном). Если частица полностью теряет свою энергию в объёме камеры, то число образовавшихся электрон-ионных пар будет пропорционально её начальной энергии, а значит, по величине собранного заряда (количеству электронов, пришедших на анод) легко определить энергию частицы. Поэтому при детектировании заряженных частиц невысоких энергий ионизационные камеры позволяют определять энергетический спектр измеряемого излучения путём измерения амплитуд импульсов на выходе детектора и построения графика плотности распределения импульсов по амплитуде. Недостатком ионизационной камеры являются очень низкие токи (амплитуды импульсов), которые трудно регистрировать. Этот недостаток преодолевается в ионизационных детекторах с газовым усилением. Газовое усиление это увеличение количества свободных зарядов в объёме детектора за счёт того, что первичные электроны на своём пути к аноду в сильных электрических полях приобретают энергию, достаточную для ударной ионизации нейтральных атомов рабочей среды детектора. В таком режиме работают пропорциональные счётчики.
Пропорциональный счётчик работает при более высокой напряжённости электрического поля, достаточной для разгона первичных электронов до такой энергии, чтобы при столкновения с нейтральными атомами ионизировать их. Но, поскольку лавинная ионизация происходит только по траектории первичной ионизирующей частицы, то сохраняется пропорциональность между энергией первичной частицы и амплитудой выходного импульса детектора. Таким образом, пропорциональный счётчик, как и ионизационная камера, способен выполнять функции спектрометра, только амплитуды выходных импульсов получаются в сотни раз больше.
Счётчики Гейгера-Мюллера.Если ещё больше увеличить разность потенциалов между анодом и катодом и довести коэффициент газового усиления до 10 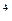 -10
-10 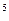 , то начинает нарушаться пропорциональность между энергией частицы, потерянной в детекторе, и величиной импульса тока. Прибор переходит в такой режим работы, когда достаточно появления в его объёме одного электрона, чтобы он запустил столь мощный лавинообразный процесс, который способен ионизировать всю область вблизи нити-анода, независимо от той локальной области, где произошёл первичный акт ионизации. При этом импульс тока достигает предельного значения (насыщается) и не зависит от первичной ионизации. Детектор, работающий подобным образом, называется счётчиком Гейгера-Мюллера. Появление в его объёме свободных носителей зарядов вызывает газовый разряд, при котором амплитуда электрического сигнала может достигать сотен вольт. При работе в импульсном (счётном) режиме детектор включается в электрическую цепь, схема которой показана на рисунке 4.1. Здесь C1– общая ёмкость детектора и входа усилителя; R1 – сопротивление нагрузки. На детектор подают высокое напряжение V, создающее в нём электрическое поле E.
, то начинает нарушаться пропорциональность между энергией частицы, потерянной в детекторе, и величиной импульса тока. Прибор переходит в такой режим работы, когда достаточно появления в его объёме одного электрона, чтобы он запустил столь мощный лавинообразный процесс, который способен ионизировать всю область вблизи нити-анода, независимо от той локальной области, где произошёл первичный акт ионизации. При этом импульс тока достигает предельного значения (насыщается) и не зависит от первичной ионизации. Детектор, работающий подобным образом, называется счётчиком Гейгера-Мюллера. Появление в его объёме свободных носителей зарядов вызывает газовый разряд, при котором амплитуда электрического сигнала может достигать сотен вольт. При работе в импульсном (счётном) режиме детектор включается в электрическую цепь, схема которой показана на рисунке 4.1. Здесь C1– общая ёмкость детектора и входа усилителя; R1 – сопротивление нагрузки. На детектор подают высокое напряжение V, создающее в нём электрическое поле E.
Рис. 4.1. Схема включения счётчика ионизирующих излучений
Наиболее распространённой является геометрия электродов в виде цилиндрического трубчатого катода и аксиально натянутой тонкой нити анода. Регистрация частиц происходит следующим образом. Частица, попадая внутрь детектора и сталкиваясь с находящимися в нём нейтральными атомами газа, вызывает их ионизацию. Электроны, тяжелые положительные и отрицательные ионы, образованные ионизирующей частицей, двигаясь в электрическом поле, испытывают многократные столкновения, упругие и неупругие, с молекулами газа. Средняя скорость направленного движения электронов и ионов пропорциональна напряжённости электрического поля и обратно пропорциональна давлению газа. Возникающий ток обусловлен в основном электронами, так как их подвижность на три порядка выше, чем подвижность тяжелых ионов. Импульс напряжения на сопротивлении R1усиливается и подаётся на регистрирующую аппаратуру.
На рисунке 4.2 [9] схематически представлены вольт-зарядные характеристики газоразрядного промежутка q = f(U) для трёх значений начальной ионизации n : 10
: 10  пар ионов от α-частицы, 10
пар ионов от α-частицы, 10 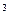 от β-частицы и 10 от гамма-излучения. Здесь предполагается, что постоянная времени τ = R1·C1много больше времени собирания заряда в детекторе. Каждую из этих кривых можно разделить на характерные участки. В отсутствие электрического поля (U=0) все ионы, созданные начальной ионизацией, полностью рекомбинируют в нейтральный газ. В электрическом поле ионы приобретают направленное движение к электродам (электроны – к аноду, а положительные ионы – к катоду), что препятствует их рекомбинации, причём их скорость зависит от напряжённости поля и подвижности образующихся заряженных частиц. При малых значениях U (участок I) происходят два конкурирующих процесса: собирание зарядов на электродах и рекомбинация ионов в газовом объёме. При увеличении поля скорость ионов увеличивается, что уменьшает вероятность рекомбинации. Однако, на этом участке число пар зарядов, уносимых полем из рабочего объёма на электроды, ещё незначительно по сравнению с числом ионов, которые рекомбинируют в том же объёме или вне его вследствие диффузии ионов в газе.
от β-частицы и 10 от гамма-излучения. Здесь предполагается, что постоянная времени τ = R1·C1много больше времени собирания заряда в детекторе. Каждую из этих кривых можно разделить на характерные участки. В отсутствие электрического поля (U=0) все ионы, созданные начальной ионизацией, полностью рекомбинируют в нейтральный газ. В электрическом поле ионы приобретают направленное движение к электродам (электроны – к аноду, а положительные ионы – к катоду), что препятствует их рекомбинации, причём их скорость зависит от напряжённости поля и подвижности образующихся заряженных частиц. При малых значениях U (участок I) происходят два конкурирующих процесса: собирание зарядов на электродах и рекомбинация ионов в газовом объёме. При увеличении поля скорость ионов увеличивается, что уменьшает вероятность рекомбинации. Однако, на этом участке число пар зарядов, уносимых полем из рабочего объёма на электроды, ещё незначительно по сравнению с числом ионов, которые рекомбинируют в том же объёме или вне его вследствие диффузии ионов в газе.
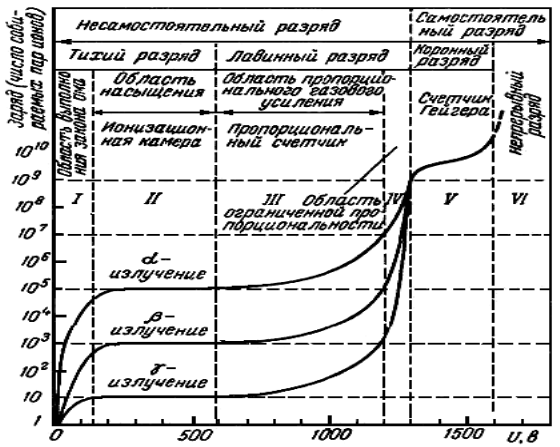
Рис. 4.2. Вольт-зарядная характеристика газонаполненного детектора
На участке I газ имеет, как и любой проводник со свободными носителями заряда, постоянную электропроводность, т.е. здесь выполняется закон Ома (с увеличением величины напряжения ток пропорционально растёт).
По мере увеличения напряжения число собираемых зарядов возрастает (конец участка I) до насыщения, при котором все заряды, созданные начальной ионизацией, оказываются полностью собранными на электродах. Рекомбинация при этом практически отсутствует. Насыщение сохраняется при дальнейшем увеличении U (горизонтальный участок II). Этот участок кривой называют областью насыщения. Именно в этой области работают ионизационные камеры. В действительности плато на участке II имеет небольшой наклон. Это объясняется тем, что при данных напряжённостях электрического поля небольшая часть образовавшихся зарядов рекомбинирует. С увеличением напряжённости поля число рекомбинаций уменьшается, и ток немного растёт. Следует иметь в виду, что в полях излучений высокой интенсивности уменьшить рекомбинацию повышением напряжения не всегда удаётся, вплоть до выхода в область пропорциональности. В таких случаях плато практически отсутствует и область выполнения закона Ома непосредственно переходит в область пропорционального газового усиления.
В области III при дальнейшем увеличении напряжения электроны, созданные в результате первичной ионизации, ускоряются полем настолько, что становятся способными при столкновении с нейтральными атомами газа ионизировать их, т.е. создавать некоторое число вторичных ионов и электронов. Происходит газовое усиление. При этом амплитуда импульса сначала растёт пропорционально первичной ионизации – это пропорциональная область. В этой области III работают пропорциональные счётчики. Область работы пропорциональных счётчиков затем сменяется областью ограниченной пропорциональности IV.
На участках III и IV образуются лавины электронов и положительных ионов, а возникший при этом разряд называется лавинным. Газовый разряд, соответствующий начальной части вольт-зарядной характеристики, включая и область насыщения (участки I и II), называется тихим разрядом. Тихий и лавинный разряды прекращаются по достижении «первичными» электронами (ионами) или их лавиной поверхности электродов, поэтому они относятся к категории несамостоятельного разряда. Лавинный разряд сопровождается явлением газового усиления, которое связано с процессами вторичной амеезации и сопровождается увеличением заряда, собираемого на электродах, по сравнению с зарядом «первичных» пар ионов. Коэффициент газового усиления, выражающий отношение этих зарядов, равен единице в области насыщения (участок II). Пройдя затем через переходную область сравнительно медленного подъёма (начало участка III), коэффициент газового усиления растёт далее с увеличением напряжения экспоненциально (участок III), а при больших напряжениях ещё быстрее из-за появления вторичных лавин от дополнительных электронов, образующихся вследствие фотоэффекта на катоде и частично в газе (участок IV). На участке напряжений III каждая лавина развивается независимо от других лавин, так что величина начальной ионизации не влияет на коэффициент газового усиления, который является здесь действительно пропорциональной константой, а сама область носит название пропорциональной области. На участке IV наиболее сильного роста газового усиления уже сказывается влияние пространственного заряда положительных ионов и соседних лавин, мешающих взаимному развитию. В этом случае величина начальной ионизации влияет на коэффициент газового усиления таким образом, что его возможный рост ограничивается при сильной первичной ионизации по сравнению с наиболее быстрым увеличением при слабой ионизации. Процессы тихого и лавинного несамостоятельного разрядов наблюдаются практически при любой геометрии электродов и не требуют большой мощности источника напряжения.
На участке V газовое усиление возрастает настолько, что собираемый заряд не зависит от первичной ионизации. Это так называемая область Гейгера. Однако разряд, как и в предыдущих областях, остаётся вынужденным, т. е. начинается после прохождения ионизирующей частицы. Это область работы счётчиков Гейгера-Мюллера. В этой области лавина за счёт фотоионизации распространяется на весь объём газа и разряд из несамостоятельного переходит в самостоятельный, за счёт чего и достигается большой коэффициент газового усиления. Но в счётчиках Гейгера-Мюллера при протекании сильного импульса тока через анодное сопротивление R1 (рис. 4.1) на нём падает практически всё напряжение источника, вследствие чего напряжённость электрического поля спадает почти до нуля, что и приводит к прекращению разряда.
Из существующих видов самостоятельного разряда для регистрации излучений используется только коронный разряд (счётчики Гейгера-Мюл-лера и коронные счётчики). Коронный разряд возникает при сравнительно больших давлениях газа во всех тех случаях, когда поле в разрядном промежутке очень неравномерно из-за малого радиуса кривизны поверхности одного или обоих электродов и достаточного расстояния между ними. Ионизация, а также свечение газа происходит лишь около электрода с малым радиусом кривизны в тонком слое, называемом короной. Коронирующий слой занимает область пробега электронных лавин, оставляющих позади себя положительные пространственные заряды большой плотности. Во внешней области коронного разряда, так называемой «тёмной», свободных электронов нет, и ток осуществляется движением ионов. Характерной особенностью коронного разряда является то, что сила тока в нём обусловлена не сопротивлением внешней цепи, а ограниченной проводимостью внешней области разряда, которая зависит от геометрии электродов, напряжения между ними, а также от природы и состояния газа. Коронный разряд возникает на участке напряжений V и прекращается после каждого единичного акта начальной ионизации принудительно: либо добавкой к наполняющему рабочий объём инертному газу одного из галогенов или органических молекул, ликвидирующих опасность вторичных лавин; либо резким ограничением мощности источника напряжения путём последовательного включения высокоомного сопротивления (108– 10 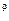 ом), которое на время движения положительных ионов к катоду сохраняет напряжение на электродах ниже порога зажигания самостоятельного коронного разряда, уменьшенного за счёт накопления отрицательного заряда на аноде в процессе разряда.
ом), которое на время движения положительных ионов к катоду сохраняет напряжение на электродах ниже порога зажигания самостоятельного коронного разряда, уменьшенного за счёт накопления отрицательного заряда на аноде в процессе разряда.
Дальнейшее увеличение напряжения приводит к непрерывному разряду (область VI), поэтому эта область для регистрации частиц не используется.
Ширина области существования прерываемой короны (участок напряжений V), после которой начинается непрерывный самостоятельный разряд (участок VI), пропорциональна величине сопротивления, включаемого последовательно с детектором для снятия выходного сигнала.
Для измерения плотности потоков заряженных частиц (альфа-, бета- и протонного излучения) преимущественно используют счётчики Гейгера-Мюллера, поскольку амплитуды выходных импульсов таких детекторов могут достигать сотен вольт и не требуют дополнительного усиления. Выходным параметром, пропорциональным плотности измеряемого потока является скорость счёта выходных импульсов (число импульсов в единицу времени). Но быстродействие счётчиков Гейгера-Мюллера невелико, что ограничивает их использование лишь для регистрации потоков невысокой интенсивности. Кроме того, они имеют ограниченный ресурс, который даже в радиационных полях средней интенсивности вырабатывается достаточно быстро. Поэтому для регистрации потоков средней и высокой интенсивности используют пропорциональные счётчики и ионизационные камеры, которые существенно превосходят счётчики Гейгера-Мюллера и по быстродействию, и по ресурсу. Кроме того, ионизационные камеры и пропорциональные счётчики благодаря пропорциональности амплитуды импульсов энергии, потерянной частицей в детекторе, позволяют производить измерение энергии регистрируемых частиц, т.е. измерять энергетический спектр исследуемого потока.
Конструкции газонаполненных детекторов существенно зависят от их назначения, т.е. определяются видом регистрируемого излучения и измеряемыми характеристиками (плотность потока, мощность экспозиционной дозы, мощность поглощённой дозы, поглощённая доза).
Измерения альфа-излучения. Для измерения альфа-излучения детектор должен иметь входное окно, закрытое очень тонкой (толщиной примерно 3 мкм) пластинкой слюды, поскольку пробег α-частиц в твёрдых веществах очень мал. Так как такая тонкая плёнка не может выдержать существенного перепада давления, то давление рабочего газа в камере делают равным среднему атмосферному давлению. Корпус детектора обычно имеет плоско-параллельную конструкцию, но не круглой а прямоугольной формы, а входное окно располагают на торцевой стороне, чтобы траектории регистрируемых α-частиц были направлены перпендикулярно направлению электрического поля в ней. В этом случае вероятность рекомбинации образовавшихся зарядов минимальна. В противном случае из-за высокой плотности концентрации образующихся вдоль траектории движения α-частицы зарядов вероятность их рекомбинации повышается и амплитуда выходных импульсов снижается.
Размеры детекторов камер для измерения α-излучения выбираются такими, чтобы средний пробег α-частиц полностью укладывался в объёме амеры. Поскольку энергия α-частиц радиоизотопных источников лежит в пределах 2-9 МэВ, то размеры получаются вполне приемлемыми (в пределах 10 см).
Измерения бета-излучения. Детекторы для измерения β-излучения устроены примерно так же, как и для измерения α-излучения. Но, хотя проникающая способность β-излучения (при той же энергии) существенно выше, чем α-излучения, но входное окно у таких детекторов всё равно приходится делать, поскольку β-излучение обладает непрерывным спектром, а их средний пробег в очень сильной степени зависит от энергии и для низкоэнергетических частиц (в единицы килоэлектронвольт) в твёрдых телах снижается до долей миллиметра). Но, чтобы отделить β-излучение от α-частиц входное окно закрывают более толстой металлической фольгой, которая поглощает все α-частицы, а β-частицы (начиная с энергий в несколько кэВ) пропускает.
Измерения гамма- и рентгеновского излучений. Гамма-кванты сравнительно редко непосредственно ионизируют нейтральные молекулы, вырывая из них электроны. Однако они передают этим электронам такую энергию, которой достаточно для ударной ионизации других молекул и атомов. Такая вторичная ионизация вносит основной вклад в суммарный ионизационный ток детектора. Но, поскольку газ в рабочем объёме детектора имеет в тысячи раз более низкую плотность, чем стенки камеры, то основная часть высокоэнергичных электронов, проникает в рабочий объём камеры из её стенок и из внешнего пространства. Первый источник быстрых электронов (за счёт первичной ионизации рабочего газа детектора) называется внутренним, второй – стеночным, а третий – внешним. Ионизационные детекторы, предназначенные для измерения γ-излучения, не имеют входного окна. Толщину стенок таких детекторов выбирают примерно равной длине свободного пробега электронов в материале корпуса (металл или стекло). Поэтому она поглощает почти все электроны внешнего источника, т.е. исключает наиболее непостоянную часть всех быстрых электронов, непосредственно производящих ионизацию газа в рабочем объёме камеры, но пропускает большую часть стеночных электронов, обеспечивая достаточно высокую чувствительность. Количество и энергия стеночных электронов зависят не только от интенсивности измеряемого γ-излучения, но и от порядкового номера Z материала корпуса. Понятно, что в токовых камерах небольших объёмов стеночный источник электронов является основным.
Ионизационные токовые камеры, предназначенные для измерения γ-излучения, не имеют входного окна. Толщина стенок таких камер примерно равна длине свободного пробега электронов в материале корпуса (металл или стекло). Поэтому она поглощает почти все электроны внешнего источника, т.е. исключает наиболее непостоянную часть всех быстрых электронов, непосредственно производящих ионизацию газа в рабочем объёме камеры, но пропускает большую часть стеночных электронов, обеспечивая достаточно высокую чувствительность. Количество и энергия стеночных электронов зависят не только от интенсивности измеряемого γ-излучения, но и от порядкового номера Z материала корпуса. Понятно, что в токовых камерах небольших объёмов (до 1 л) стеночный источник электронов является основным. Поэтому такие камеры иногда называют стеночными.
Поскольку доза и мощность дозы рентгеновского и γ-излучения определяется по степени ионизации воздуха (экспозиционная доза), то дозиметр на основе токовой камеры будет давать правильные показания в том случае, когда стенки камеры будут состоять из вещества с массовым коэффициентом поглощения γ-излучения равным массовому коэффициенту поглощения воздуха. Такие вещества называют воздухоэквивалентными. К ним относятся бакелит, плексиглас, полистирол, полиэтилен и ряд других пластмасс. Количество и энергия вторичных электронов, возникающих в единице массы такого вещества и воздуха под действием γ-излучения практически одинаковы. Такие камеры называют воздухоэквивалентными.
Однако ионизационный ток камеры зависит не только от интенсивности измеряемого гамма-излучения, но и от давления и природы газа-наполнителя, материала и толщины стенок и энергии γ-квантов. Поэтому токовые камеры обязательно градуируются с помощью так называемых «нормальных» камер. Это плоские открытые камеры, в которых рабочим газом является наружный воздух или большие цилиндрические камеры, наружные стенки которых изготовлены из крупноячеистой сетки, которая практически не влияет на измеряемое γ-излучение. Следовательно, в них отсутствует стеночный источник электронов, и остаются только внутренний и внешний источники. Поскольку объём воздуха в полости камеры много меньше объёма окружающего пространства, из которого могут прилетать свободные электроны, то газ внутри такой камеры ионизируется главным образом за счёт электронов внешнего источника. Им можно считать слой воздуха, окружающий рабочий объём камеры, толщиной, равной средней длине свободного пробега электронов соответствующей энергии в воздухе. Поэтому ионизационный ток нормальной камеры наиболее точно соответствует интенсивности вызывающего его γ-излучения. Это позволяет достаточно точно рассчитывать ионизационный ток в такой камере в зависимости от интенсивности γ-излучения и градуировать по показаниям нормальной камеры обычную закрытую камеру.
Теперь рассмотрим вопрос о выборе газа и его давления в ионизационных камерах. В таблице 4.1 [20] представлены сравнительные данные ионизирующего действия γ-излучения радиевого изотопного источника на различные газы при нормальных условиях (температура 20 0С, давление 101,3 кПа). В ней приведены значения ионизации – число I образованных пар ионов в 1 см3 за 1 с для данных газов.
Таблица 4.1
Ионизирующее действие γ-излучения для различных газов
| Газ-наполнитель | I | Газ-наполнитель | I | |
| Водород | 0,99 | Неон | 4,25 | |
| Гелий | 1,00 | Аргон | 8,51 | |
| Кислород | 5,82 | Криптон | 19,40 | |
| Воздух | 5,08 | Ксенон | 31,90 | |
| Углекислый газ | 8,70 |
Помимо степени ионизации важное значение при выборе газа-наполнителя имеет вероятность образования отрицательных ионов при взаимодействии с электронами, характеризуемая так называемым «коэффициентом прилипания», поскольку это влияет на степень рекомбинации образовавшихся зарядов, а значит, и на их собираемость на электродах. С этой точки зрения кислород, а значит, и воздух имеют величину такого коэффициента примерно в 100 раз больше, чем инертные газы: неон, аргон, криптон и ксенон. Поэтому камеры, заполненные воздухом, требуют более высокой напряжённости электрического поля и, тем не менее, не обеспечивают достижения полного насыщения ионизационного тока, что объясняется влиянием рекомбинации. А при отсутствии полного насыщения ионизационный ток в камере зависит и от температуры, и от давления газа, что объясняется именно влиянием рекомбинации, поскольку температура оказывает влияние на интенсивность диффузии, среднюю скорость теплового движения молекул, а значит и на интенсивность процессов рекомбинации. Влияние давления на ионизационный ток уже рассматривалось выше (зависимость неоднозначная и имеет максимум), но для температурного коэффициента зависимость от давления монотонная: с ростом давления температурный коэффициент тока ионизации растёт.
Ионизационный ток зависит и от энергии γ-квантов. Для всех газов эта зависимость имеет близкий характер: сначала при росте энергии γ-квантов ионизационный ток растёт, затем он достигает максимума и при дальнейшем возрастании энергии излучения либо сохраняется неизменным, либо слабо падает. Чтобы уменьшить влияние энергии γ-излучения на величину ионизационного тока корпус ионизационных камер следует изготавливать из материалов с атомным номером близким к атомному номеру газа-наполнителя. Если газом наполнителем является воздух (что используется в ионизационных камерах, предназначенных для измерения экспозиционной дозы облучения), то корпус делается из воздухоэквивалентного материала (пластмасс). Если же камера заполняется тяжёлыми инертными газами (аргон, криптон), то корпус изготавливается из латуни или стали.
Date: 2021-06-08; view: 1392; Нарушение авторских прав
Магнитный поток
Вектор магнитной индукции →B характеризует магнитное поле в каждой точке пространства.
Можно ввести еще одну величину, зависящую от значения вектора →B не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром.
Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль →n к плоскости проводника составляет угол α с направлением вектора магнитной индукции →B (см. рисунок).
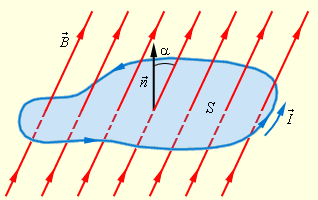
Произведение Bcos.α=Bn представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:
Φ=BnS
Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.
Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.
Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?
Выразим модуль вектора магнитной индукции:
В=ΦScos.α..
Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:
0,20,5cos.(90°−30°)..=0,20,5·0,5..=0,8 (Тл)













































