Примеры гидравлических расчетов. пример 5.1. на оси водопроводной трубы установлена трубка пито с дифференциальным ртутным манометром
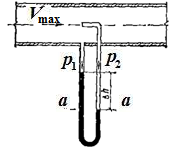
Пример 5.1. На оси водопроводной трубы установлена трубка Пито с дифференциальным ртутным манометром. Определить максимальную скорость движения воды в трубе Vmax, если разность уровней ртути в манометре Δh = 18 мм.
 Решение:
Решение:
Трубка Пито измеряет скоростной напор
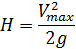
Откуда 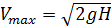
Для определения Н запишем уравнение равновесия в ртутном манометре относительно плоскости а-а
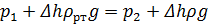
где 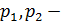 давления в трубках ртутного манометра на уровне верхней отметки ртути;
давления в трубках ртутного манометра на уровне верхней отметки ртути;  – плотность ртути (13600 кг/м3) и воды (1000 кг/м3).
– плотность ртути (13600 кг/м3) и воды (1000 кг/м3).
Отсюда получаем
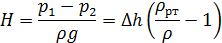
Подставляя исходные данные, получим
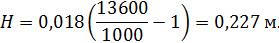
Таким образом, максимальная скорость в трубе
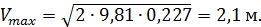
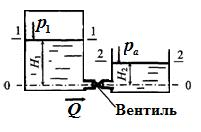
Пример 5.2. Горизонтальная труба диаметром d = 5 см соединяет резервуары с водой, в которых поддерживаются постоянные уровни Н1 = 4,5 м и H2 = 2,5 м. Для регулирования расхода на трубопроводе установлен вентиль. Определить коэффициент сопротивления вентиля и потерю напора в нем, если расход воды Q = 12,5 л/с, а избыточное давление на поверхности воды в напорном баке ризб = 25 кПа. Другими потерями напора пренебречь.
Решение:
Перед записью уравнения Бернулли выбираем два сечения.
В качестве начального сечения принимаем открытую поверхность жидкости в напорном баке и обозначаем его 1-1. В пределах этого сечения скорость жидкости мала V1 ≈ 0, абсолютное давление р1 = ра ризб. Конечное сечение выбираем на поверхности жидкости в сливном баке 2-2. В пределах этого сечения скорость V2 ≈ 0, абсолютное давление р2 = ра.
В качестве произвольной горизонтальной плоскости для отсчета нивелирных высот (сечение 0-0) выбираем плоскость, совпадающую с осью трубопровода. Тогда z1 = H1, а z2 = H2.
В соответствии с условием задачи учитываем только местные потери напора на вентиле hв, тогда уравнение Бернулли принимает вид:
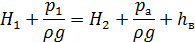
Выразим потери напора на вентиле
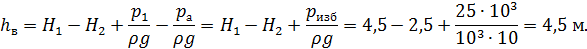
С другой стороны, потери напора можно определить по формуле Вейсбаха
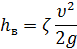
Скорость движения жидкости выразим из уравнения неразрывности потока
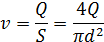
Подставив в формулу и выразив коэффициент сопротивления, окончательно получаем:
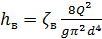 ;
;
Следовательно,
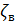 =
= 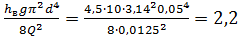
§
Для решения задачи с применением уравнения Бернулли следует:
1) выбрать два сечения, для которых записывается уравнение. В качестве сечений рекомендуется брать:
– выход в атмосферу, где  абс = ра;
абс = ра;
– свободную поверхность в резервуаре, где скорость V = 0
– сечение, в котором присоединен прибор для измерения давления (манометр, вакуумметр, пьезометр и др.).
2) записать уравнение Бернулли в общем виде – формула (5.1) для идеальной жидкости и формула (5.2) для реальной жидкости;
3) переписать уравнение для заданных сечений с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.
При этом необходимо помнить:
– уравнение Бернулли записывается по течению жидкости;
– вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;
– давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);
– коэффициент Кориолиса в задачах на движение потока реальной жидкости следует учитывать только при ламинарном режиме течения α = 2, для турбулентных потоков можно принимать α = 1;
– суммарная потеря напора 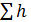 записывается в правой части уравнения со знаком « » и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.
записывается в правой части уравнения со знаком « » и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.
§
Задачи
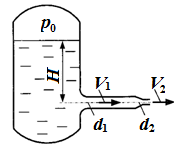 Задача 5.1. Из напорного бака вода течет по трубе диаметром d1 = 20 мм и затем вытекает в атмосферу через брандспойт с диаметром выходного отверстия d2 = 10 мм. Избыточное давление воздуха в баке р0 = 0,18 МПа; высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V1 и на выходе
Задача 5.1. Из напорного бака вода течет по трубе диаметром d1 = 20 мм и затем вытекает в атмосферу через брандспойт с диаметром выходного отверстия d2 = 10 мм. Избыточное давление воздуха в баке р0 = 0,18 МПа; высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V1 и на выходе
из насадка V2.
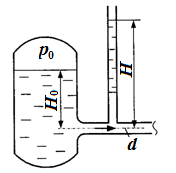
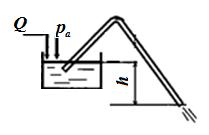 Задача 5.2. Определить скорость движения бензина V и расход Q в сифонном трубопроводе. Нижняя точка оси трубопровода расположена ниже уровня жидкости в питающем резервуаре на расстоянии h = 2,5 м. Внутренний диаметр трубопровода d = 25 мм, плотность бензина ρ = 850 кг/м3. Потерями напора пренебречь.
Задача 5.2. Определить скорость движения бензина V и расход Q в сифонном трубопроводе. Нижняя точка оси трубопровода расположена ниже уровня жидкости в питающем резервуаре на расстоянии h = 2,5 м. Внутренний диаметр трубопровода d = 25 мм, плотность бензина ρ = 850 кг/м3. Потерями напора пренебречь.
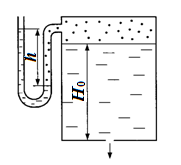
Задача 5.3. Определить расход жидкости Ж, вытекающей из бака по трубопроводу диаметром d, если избыточное давление воздуха в баке р0, высота уровня Н0, высота подъема жидкости в пьезометре, открытом в атмосферу Н. Потерями энергии пренебречь.
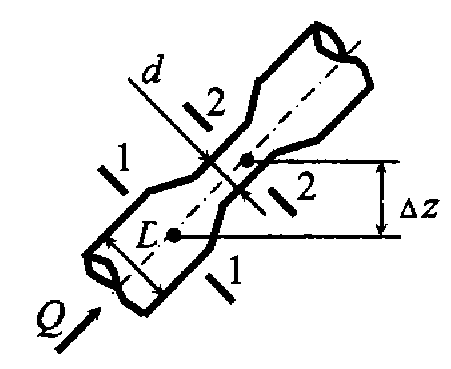 Задача 5.4. Вода движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление больше в сечении 1-1 Δр = 25 кПа. Определить расход Q, если внутренний диаметр трубопровода в сечении 1-1 D = 65 мм, а в сечении 2-2 d = 40 мм, разность отметок сечений Δz = 2 м. Потерями напора пренебречь.
Задача 5.4. Вода движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление больше в сечении 1-1 Δр = 25 кПа. Определить расход Q, если внутренний диаметр трубопровода в сечении 1-1 D = 65 мм, а в сечении 2-2 d = 40 мм, разность отметок сечений Δz = 2 м. Потерями напора пренебречь.
Задача 5.5. Керосин движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление в сечении 1-1 р1 = 35 кПа. Определить избыточное давление в сечении 2-2, если внутренний диаметр трубопровода в сечении 1-1 D = 50 мм, а в сечении 2-2 d = 35 мм, разность отметок сечений Δz = 1 м, расход Q = 2 л/с. Потерями напора пренебречь.
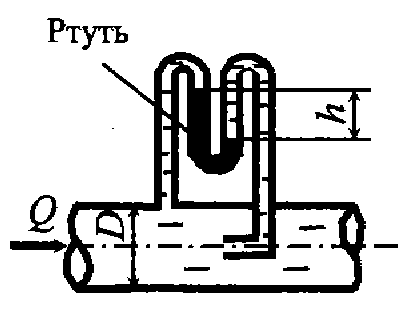 Задача 5.6. Определить расход воды в трубопроводе, если согласно показаниям ртутного дифференциального манометра h = 30 мм. Плотность ртути ρ = 13600 кг/м3, внутренний диаметр трубопровода D = 80 мм. Потери напора не учитывать.
Задача 5.6. Определить расход воды в трубопроводе, если согласно показаниям ртутного дифференциального манометра h = 30 мм. Плотность ртути ρ = 13600 кг/м3, внутренний диаметр трубопровода D = 80 мм. Потери напора не учитывать.
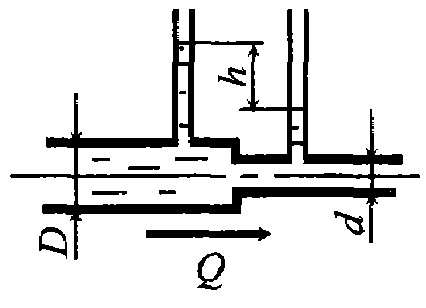 Задача 5.7. По горизонтальной трубе переменного сечения протекает нефть с расходом Q = 1,3 л/с. Определить разность показаний пьезометров h, если диаметр трубопровода в широком сечении D = 10 см, а в узком d = 5 см. Плотность нефти ρ = 850 кг/м3. Потерями напора пренебречь.
Задача 5.7. По горизонтальной трубе переменного сечения протекает нефть с расходом Q = 1,3 л/с. Определить разность показаний пьезометров h, если диаметр трубопровода в широком сечении D = 10 см, а в узком d = 5 см. Плотность нефти ρ = 850 кг/м3. Потерями напора пренебречь.
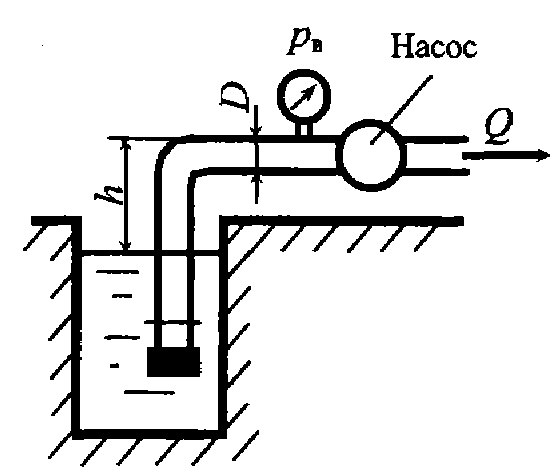 Задача 5.8. Насос с подачей Q = 7,2 м3/ч забирает воду из колодца. Определить наибольший вакуум pвак при входе в насос. Внутренний диаметр трубопровода D = 80 мм, высота установки насоса над уровнем жидкости h = 4 м. Потери напора Δh = 0,5 м.
Задача 5.8. Насос с подачей Q = 7,2 м3/ч забирает воду из колодца. Определить наибольший вакуум pвак при входе в насос. Внутренний диаметр трубопровода D = 80 мм, высота установки насоса над уровнем жидкости h = 4 м. Потери напора Δh = 0,5 м.
Задача 5.9. По трубопроводу диаметром D = 150 мм движется вода с расходом 20 л/мин. Определить, пренебрегая потерями напора, разность уровней в жидкостном манометре. Плотность жидкости в манометре ρ = 1300 кг/м3.
Задача 5.10.Нефть движется под напором в трубопроводе квадратного сечения. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости, если сторона квадрата a = 0,05 м, динамический коэффициент вязкости μ = 0,02 Па·с, а плотность нефти ρ = 850 кг/м3.
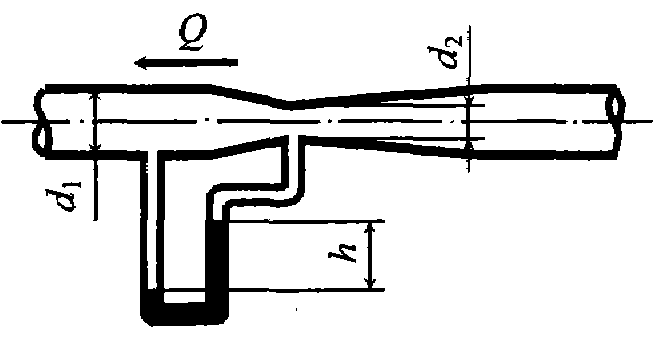 Задача 5.11.По горизонтальному трубопроводу переменного сечения движется нефть, плотность которой ρ = 850 кг/м3. Диаметр в широком сечении трубопровода d1 =50 мм. Расход жидкости в трубопроводе Q = 0,5 л/с, разность уровней в дифференциальном манометре, заполненном ртутью плотностью ρ = 13600кг/м3, составляет h = 35 мм. Определить диаметр трубопровода в узком сечении. Потерями напора пренебречь.
Задача 5.11.По горизонтальному трубопроводу переменного сечения движется нефть, плотность которой ρ = 850 кг/м3. Диаметр в широком сечении трубопровода d1 =50 мм. Расход жидкости в трубопроводе Q = 0,5 л/с, разность уровней в дифференциальном манометре, заполненном ртутью плотностью ρ = 13600кг/м3, составляет h = 35 мм. Определить диаметр трубопровода в узком сечении. Потерями напора пренебречь.
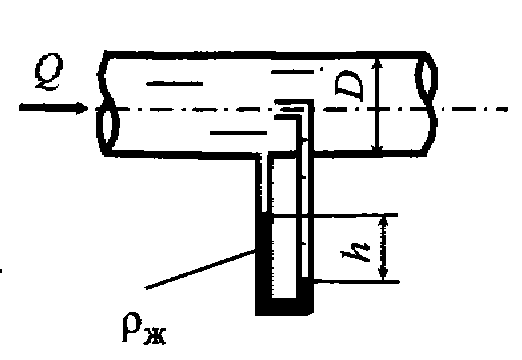 Задача 5.12.Определить скорость и расход газа с плотностью ρ = 20 кг/м3 в трубопроводе с внутренним диаметром D = 50 мм. В колене манометра находится жидкость плотностью ρж = 1000 кг/м3. Потери напора не учитывать.
Задача 5.12.Определить скорость и расход газа с плотностью ρ = 20 кг/м3 в трубопроводе с внутренним диаметром D = 50 мм. В колене манометра находится жидкость плотностью ρж = 1000 кг/м3. Потери напора не учитывать.
Задача 5.13. По горизонтальному трубопроводу переменного сечения движется вода. Из бачка А по трубке, подведенной к трубопроводу, поступает краситель, имеющий плотность ρ = 1300 кг/м3. Определить расход воды в трубопроводе, при котором прекратится подача красителя. Уровень красителя в 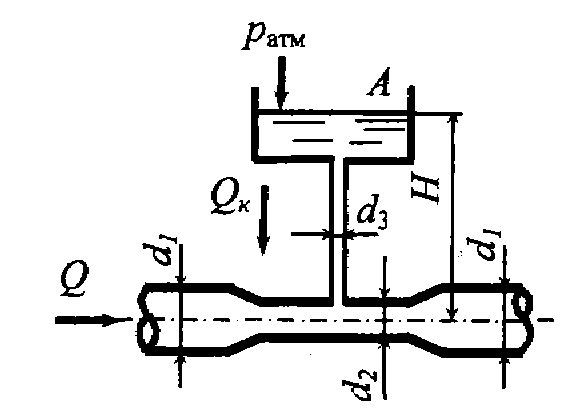 бачке H = 0,5 м, диаметр трубопровода в широком сечении d1 = 150 мм, в узком – d2 = 100 мм, избыточное давление воды в широком сечении трубопровода составляет 30 кПа. Потерями напора пренебречь.
бачке H = 0,5 м, диаметр трубопровода в широком сечении d1 = 150 мм, в узком – d2 = 100 мм, избыточное давление воды в широком сечении трубопровода составляет 30 кПа. Потерями напора пренебречь.
Задача 5.14. Для условий задачи 4.13 определить, при какой высоте Н прекратится подача красителя. Расход воды в трубопроводе Q = 1,8 м3/мин, диаметр трубопровода в широком сечении d1 = 200 мм, в узком – d2 = 100 мм, абсолютное давление воды в широком сечении трубопровода составляет 150 кПа. Потерями напора пренебречь.
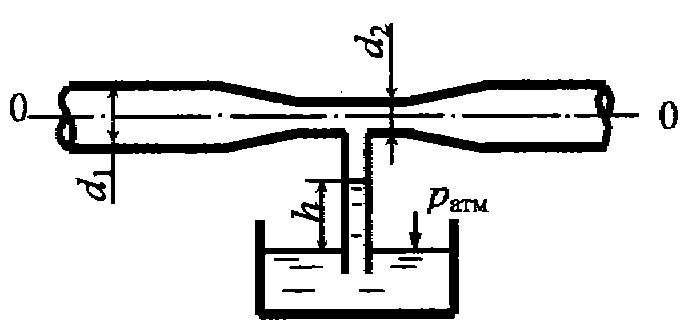 Задача 5.15. Определить давление в сечении трубопровода с диаметром d1 = 0,1 м, если вода в трубке поднялась на высоту h = 3 м, диаметр cуженой части трубопровода d2 = 0,6 м, расход воды в трубопроводе Q = 0,0065 л/с. Потери напора не учитывать.
Задача 5.15. Определить давление в сечении трубопровода с диаметром d1 = 0,1 м, если вода в трубке поднялась на высоту h = 3 м, диаметр cуженой части трубопровода d2 = 0,6 м, расход воды в трубопроводе Q = 0,0065 л/с. Потери напора не учитывать.
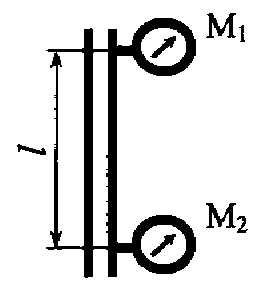 Задача 5.16. На вертикальной водопроводной трубе постоянного диаметра на расстоянии l = 10 м установлены два манометра. Нижний манометр показывает давление 1,2 кг/см2, а верхний – 0,8 кг/см2. Определить гидравлический уклон и направление движения жидкости.
Задача 5.16. На вертикальной водопроводной трубе постоянного диаметра на расстоянии l = 10 м установлены два манометра. Нижний манометр показывает давление 1,2 кг/см2, а верхний – 0,8 кг/см2. Определить гидравлический уклон и направление движения жидкости.
Задача 5.17. По нагнетательному патрубку диаметром d1 = 200 мм вентилятором подается воздух плотностью ρ = 1,2 кг/м3 с расходом Q = 0,8 м3/с при избыточном давлении р1 = 1 кПа. К патрубку подсоединен диффузор с диаметром выходного сечения d2 = 300 мм. Определить давление воздуха на выходе из диффузора. Изменение плотности воздуха и потери в диффузоре не учитывать.
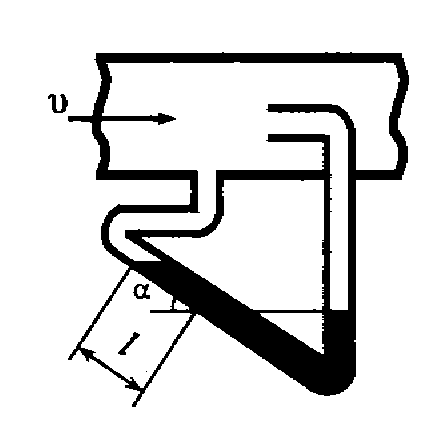 Задача 5.18. К трубе, по которой движутся дымовые газы плотностью ρ = 0,6 кг/м3, присоединен микроманометр, заполненный спиртом (ρсп = 0,6 кг/м3). Показание шкалы манометра, наклоненной под углом α = 30° к горизонту, l = 15 мм. Определить скорость движения дымовых газов.
Задача 5.18. К трубе, по которой движутся дымовые газы плотностью ρ = 0,6 кг/м3, присоединен микроманометр, заполненный спиртом (ρсп = 0,6 кг/м3). Показание шкалы манометра, наклоненной под углом α = 30° к горизонту, l = 15 мм. Определить скорость движения дымовых газов.
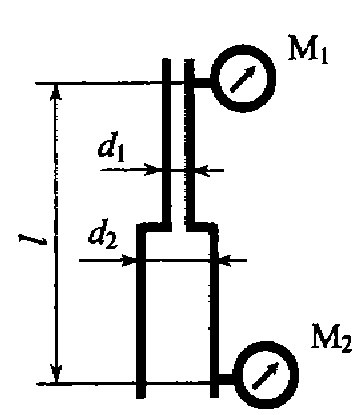 Задача 5.19. На вертикальной водопроводной трубе, состоящей из труб диаметром d1 = 27 мм и d2 = 15 мм, установлены два манометра. Нижний манометр показывает давление 1,6 кг/см2, а верхний – 1,2 кг/см2. Определить направление движения воды, гидравлический и пьезометрический уклоны, если расход составляет Q = 0,3 л/с.
Задача 5.19. На вертикальной водопроводной трубе, состоящей из труб диаметром d1 = 27 мм и d2 = 15 мм, установлены два манометра. Нижний манометр показывает давление 1,6 кг/см2, а верхний – 1,2 кг/см2. Определить направление движения воды, гидравлический и пьезометрический уклоны, если расход составляет Q = 0,3 л/с.
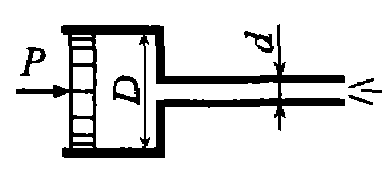 Задача 5.20. Поршень диаметром D = 200 мм вытесняет воду по короткому трубопроводу диаметром d = 20 мм в атмосферу. Определить усилие на поршень, если скорость истечения жидкости v = 5 м/с, потери напора hw = 2 м.
Задача 5.20. Поршень диаметром D = 200 мм вытесняет воду по короткому трубопроводу диаметром d = 20 мм в атмосферу. Определить усилие на поршень, если скорость истечения жидкости v = 5 м/с, потери напора hw = 2 м.
Контрольные вопросы и задания
1. Напишите уравнение Бернулли для элементарной струйки движущейся жидкости и объясните, какие параметры оно связывает.
2. Объясните геометрический и энергетический смысл уравнения Бернулли?
3. Чем отличается уравнение Бернулли для потока реальной жидкости от уравнения, составленного для элементарной струйки идеальной жидкости?
4. Чем обусловлены потери напора в потоке реальной жидкости?
5. Что такое гидродинамический напор? Чему он равен?
6. От чего зависит скоростной напор и чему он равен?
1. Использование уравнения Бернулли в приборах для измерения скорости.
2. Трубчатый расходомер Вентури.
3. Устройство и принцип действия струйного насоса.
§
Все трубопроводы подразделяются на две категории: простые и сложные. Простой трубопровод не имеет разветвлений на пути движения жидкости, но может представлять последовательное соединение труб разного диаметра. Сложный трубопровод имеет хотя бы одно разветвление и может содержать как параллельные и последовательные соединения труб.
Если в трубопроводе необходимо обеспечить расход жидкости Q, то потребный для этого напор Нпотр. – пьезометрическая высота в начальном сечении определяется по формуле
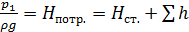 , (6.1)
, (6.1)
где 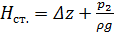 – статический напор,
– статический напор, 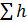 – суммарные потери напора на сопротивление в трубопроводе.
– суммарные потери напора на сопротивление в трубопроводе.
Суммарная потеря напора складывается из потерь на трение по всей длине трубы и местных потерь
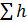 =
=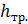
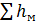
Для определения потерь напора на трение в трубах круглого сечения можно использовать формулу Дарси, которую для дальнейших расчетов удобно выразить через расход:
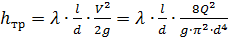 (6.2)
(6.2)
где l – длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
При турбулентном движении коэффициент трениязависит от числа Рейнольдса 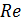 и относительной шероховатости трубы ε
и относительной шероховатости трубы ε 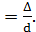 Значения эквивалентной (абсолютной) шероховатости Δ для различных труб представлены в Приложении 7.
Значения эквивалентной (абсолютной) шероховатости Δ для различных труб представлены в Приложении 7.
Универсальной формулой, учитывающей одновременно оба фактора является формула Альтшуля:
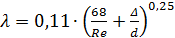 (6.3)
(6.3)
Для гидравлически гладких труб шероховатость на сопротивление не влияет, и коэффициент сопротивления 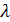 однозначно определяется числом Рейнольдса:
однозначно определяется числом Рейнольдса:
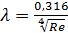 (6.4)
(6.4)
Местные потери напораопределяются по формуле Вейсбаха:
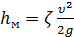 (6.5)
(6.5)
где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами).
C учетом формул Дарси и Вейсбаха,
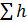 =
=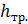
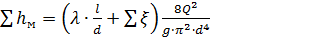 (6.6)
(6.6)
При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):
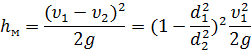
Обозначим 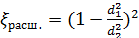 – коэффициент местных сопротивлений при расширении трубы, где d1 и d2 – внутренние диаметры сечений трубы перед и за расширением.
– коэффициент местных сопротивлений при расширении трубы, где d1 и d2 – внутренние диаметры сечений трубы перед и за расширением.
В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен
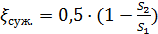 ,
,
где S1 и S2 – площади сечений трубы до и после сужения.
Формула (6.6) справедлива для обоих режимов, однако для ламинарного режима удобнее использовать формулу Пуазейля:

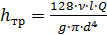 , (6.7)
, (6.7)
в которой необходимо заменить фактическую длину трубопровода расчетной, равной
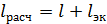 ,
,
где 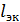 – длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе.
– длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе.
Формула для расчета потребного напора имеет вид
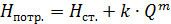 , (6.8)
, (6.8)
где для ламинарного режима течения

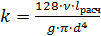 , m=1; (6.9)
, m=1; (6.9)
турбулентного режима течения
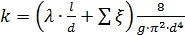 , m=2 (6.10)
, m=2 (6.10)
Характеристики потребного напора 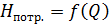 и суммарных потерь напора трубопроводов
и суммарных потерь напора трубопроводов 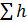 =
=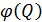 при ламинарном режиме представляет прямые, при турбулентном – параболы.
при ламинарном режиме представляет прямые, при турбулентном – параболы.
§
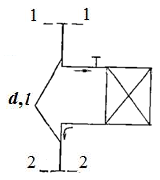
Пример 6.1.Расход горячей воды с температурой 95°С через радиатор водяного отопления Q = 0,1 м3/ч. Определить потери давления между сечениями 1-1 и 2-2, если диаметр подводящих трубопроводов d = 0,0125 м, а их общая длина l = 5 м. Принять следующие коэффициенты сопротивления: для поворота ζ1 = 1,45 для крана ζ2 = 0,5, для радиатора ζ3 = 2,1.
 Решение:
Решение:
Суммарные потери давления складываются из потерь давления по длине и местных потерь:
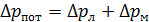
Средняя скорость движения воды в трубопроводе:
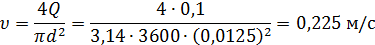
Число Рейнольдса определяем с учетом того, что кинематический коэффициент вязкости воды при температуре 95°С ν = 0,3·10-6 м2/с (табл.4.5):
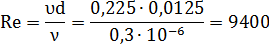
Абсолютная шероховатость стальной трубы 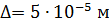 (Приложение 7), относительная шероховатость
(Приложение 7), относительная шероховатость
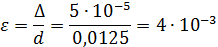
Таким образом, коэффициент гидравлического трения определяем по формуле:
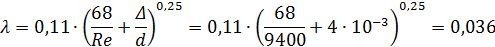
Вычислим потери давления по длине при плотности воды ρ = 961,9 кг/м3 (табл.4.1):
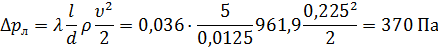
Местные потери давления складываются из потерь на поворот, в пробковом кране и в радиаторе:
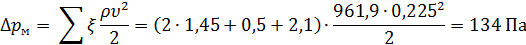
Суммарные потери давления
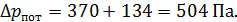
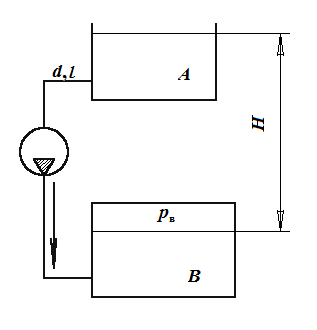
Пример 6.2. Вода, перекачивается насосом из открытого бака А в расположенный ниже резервуар B, где поддерживается постоянное давление рв = 0,18 МПа (абс.) по трубопроводу общей длиной  = 225 м и диаметром
= 225 м и диаметром 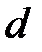 =250 мм. Разность уровней воды в баках h=3 м. Определить потребный напор, создаваемый насосом для подачи в бак B расхода воды
=250 мм. Разность уровней воды в баках h=3 м. Определить потребный напор, создаваемый насосом для подачи в бак B расхода воды  = 98 л/с. Принять суммарный коэффициент местных сопротивлений ζ = 6,5. Эквивалентная шероховатость стенок трубопровода Δ = 0,15 мм. Жидкость – вода с плотностью ρ = 1000 кг/м3 и вязкостью ν = 0,01 Ст. Атмосферное давление ра = 0,1 МПа.
= 98 л/с. Принять суммарный коэффициент местных сопротивлений ζ = 6,5. Эквивалентная шероховатость стенок трубопровода Δ = 0,15 мм. Жидкость – вода с плотностью ρ = 1000 кг/м3 и вязкостью ν = 0,01 Ст. Атмосферное давление ра = 0,1 МПа.
 Решение:
Решение:
Потребный напор, создаваемый насосом для подачи в бак B расхода воды  равен
равен
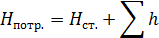
Статический напор складывается из пьезометрической высоты на поверхности жидкости в резервуаре В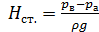 и разности уровней воды в резервуарах h. Т.к. вода перекачивается в нижний бак, то вторую составляющую подставляем со знаком «-».
и разности уровней воды в резервуарах h. Т.к. вода перекачивается в нижний бак, то вторую составляющую подставляем со знаком «-».
Потери напора 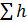 складываются из потерь напора на трение по длине трубопровода
складываются из потерь напора на трение по длине трубопровода 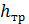 и потерь на местных сопротивлениях
и потерь на местных сопротивлениях 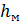 .
.
Таким образом
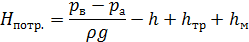
Потери напора 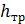 по длине трубопровода определим по формуле Дарси, записав ее через расход:
по длине трубопровода определим по формуле Дарси, записав ее через расход:
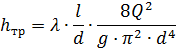
Для правильного вычисления коэффициента трения λ определим режим течения жидкости в трубопроводе:
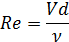
Согласно уравнению неразрывности скорость движения жидкости в трубопроводе
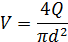
Тогда формула числа Рейнольдса примет вид:
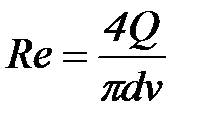
Подставив значения, определим режим течения жидкости:
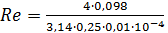 = 499110
= 499110 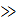 2320
2320
Величина числа Рейнольдса указывает на турбулентный режим движения. Для такого значения числа 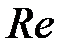 коэффициент трения вычислим по универсальной формуле Альтшуля:
коэффициент трения вычислим по универсальной формуле Альтшуля:
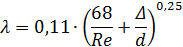
Вычислим коэффициент Дарси:
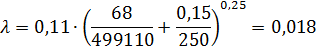
Вычислим потери напора 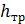 по длине трубопровода
по длине трубопровода
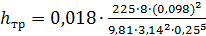 =3,291 м.
=3,291 м.
Местные потери напора 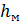 определим по формуле Вейсбаха, записав ее через расход:
определим по формуле Вейсбаха, записав ее через расход: 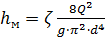
Вычислим местные потери 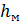 :
:
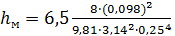 = 1,32 м.
= 1,32 м.
Окончательно подставив полученные значения, определим потребный напор, используя для расчета избыточное давление в баке В:
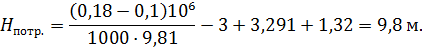
§
Задачи на расчет простого трубопровода делятся на три типа.
1 тип. Даны: расход жидкости Q в трубопроводе, его геометрические параметры (l,d,Δz), шероховатость труб; давление в конечном сечении (либо в начальном для всасывающих трубопроводов) и свойства жидкости (ρ,ν). Местные сопротивления заданы коэффициентами ζ либо оцениваются по справочным данным.
Требуется найти потребный напор Hпотр.
Алгоритм решения:
1) Определить режим течения. С этой целью нужно найти число Рейнольдса Re по известным Q, d и ν.
2) При ламинарном режиме напор вычисляется по формулам (6.7) и (6.8)
3) При турбулентном режиме задача решается с помощью формул (6.3) или (6.4) в зависимости от шероховатости труб (Пример 6.2).
2 тип. Даны: располагаемый напор Hрасп, все величины, перечисленные в задаче 1-го типа, кроме расхода Q.
Так как число Рейнольдса Re нельзя вычислить, то режимом движения необходимо задаться, основываясь на роде жидкости. Для вязких жидкостей (масло) выбирать ламинарный режим течения, для маловязких (вода, бензин, керосин) – турбулентный. Для проверки правильности выбора в конце решения необходимо вычислить число Рейнольдса. Либо по формулам (6.7) и (6.8) выразить диаметр через критическое число Рейнольдса и определить Hкр, соответствующее смене режима. Сравнивая Hкр и Hрасп, определяют режим течения.
При ламинарном режиме задача решается на основании формул (6.7) и (6.8).
При турбулентном режиме в уравнениях (6.7) и (6.9) содержаться две неизвестные Q и λт, зависящие от числа Рейнольдса. В этом случае для решения задачи требуется метод последовательных приближений. Для этого в первом приближении следует задаться коэффициентом λт. Выбрав начальное значение λт, решить задачу по 1-му типу. По полученным данным следует заново найти λт и повторить все вычисления, приближаясь к истинному результату.
3 тип. Даны: располагаемый напор Hрасп, расход жидкости Q в трубопроводе, его геометрические параметры и свойства жидкости, перечисленные выше, кроме диаметра трубопровода d.
Так как число Рейнольдса Re нельзя вычислить, то режимом движения либо необходимо задаться, либо по формулам (6.7) и (6.8) выразить диаметр через критическое число Рейнольдса и определить Hкр, соответствующее смене режима. Сравнивая Hкр и Hрасп, определяют режим течения.
При ламинарном режиме задача решается на основании формул (6.7) и (6.8).
При турбулентном режиме решение нужно проводить с использованием графиков. Для этого следует
1) задать ряд значений диаметра d и по ним подсчитать Hпотр;
2) построить график Hпотр = f(d);
3) по графику, зная Hрасп, определить d.
§
Задачи
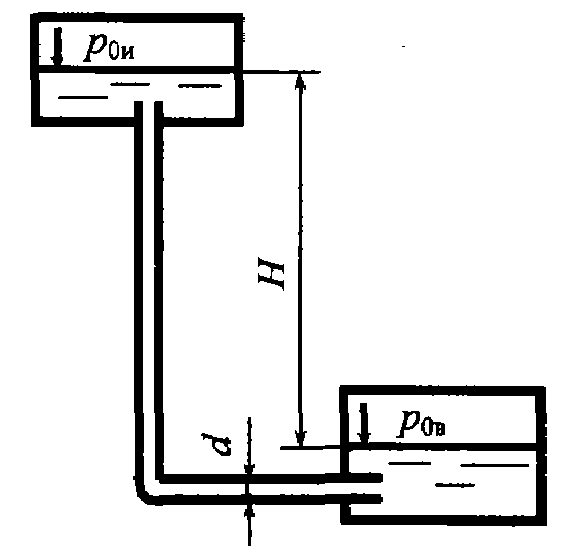 Задача 6.1. По трубопроводу, соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает вода с плотностью ρ = 1000 кг/м3. Диаметр трубопровода d = 20 мм. В верхнем баке поддерживается избыточное давление р0изб = 15 кПа, а в нижнем – вакуумметрическое давление р0вак = 7 кПа. Разность уровней в баках H = 5 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,028, а длина трубопровода l = 15 м. Местными потерями напора пренебречь.
Задача 6.1. По трубопроводу, соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает вода с плотностью ρ = 1000 кг/м3. Диаметр трубопровода d = 20 мм. В верхнем баке поддерживается избыточное давление р0изб = 15 кПа, а в нижнем – вакуумметрическое давление р0вак = 7 кПа. Разность уровней в баках H = 5 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,028, а длина трубопровода l = 15 м. Местными потерями напора пренебречь.
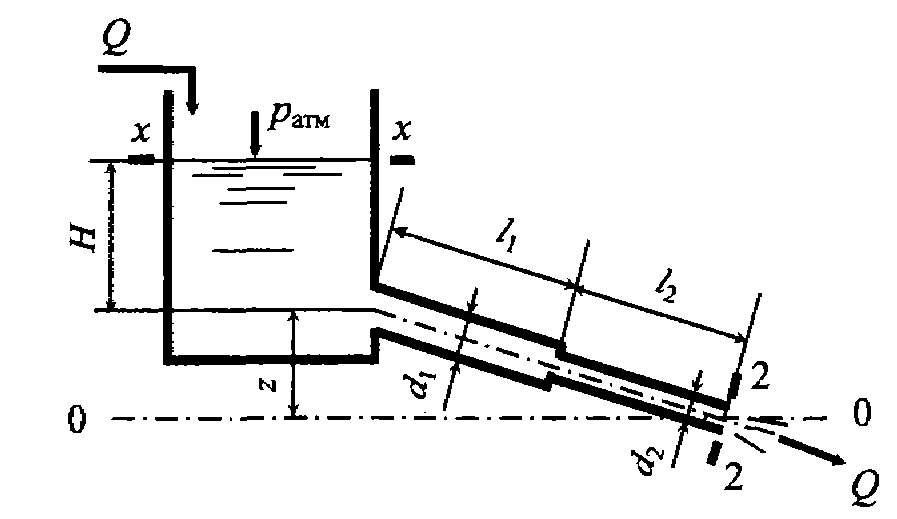
Задача 6.2.Из напорного бака по наклонному трубопроводу переменного сечения движется жидкость с относительной плотностью δ = 0,85. Диаметры участков трубопровода d1 = 50 мм, d2 = 30 мм, а длина соответственно равна l1 = 80 м, l2 = 40 м. Начало трубопровода расположено выше его конца на величину z = 3,5 м. Для обоих участков трубопровода коэффициент гидравлического трения λ = 0,038. Какой уровень Н необходимо поддерживать в напорном баке, чтобы скорость движения жидкости на выходе из трубопровода была v = 1,8 м/с? Местными потерями напора пренебречь.
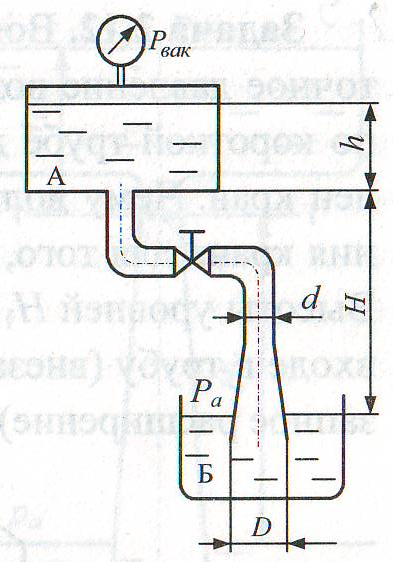 Задача 6.3. Вода перетекает из бака А в бак Б по трубе диаметром d = 25 мм, на которой установлены вентиль с коэффициентом сопротивления ζв = 3,5, а также диффузор с ζд = 0,5 и диаметром выходного отверстия D = 75 мм. Показание вакуумметра pвак = 10 кПа, высота Н = 2,5 м, h = 2 м. Определить расход Q c учетом всех местных сопротивлений. При решении потерями на трение пренебречь, принять коэффициент сопротивления каждого колена ζкол = 0,5, учесть потери напора на входе в трубу (внезапное сужение) и на выходе в бак (внезапное расширение). Взаимным влиянием сопротивлений пренебречь.
Задача 6.3. Вода перетекает из бака А в бак Б по трубе диаметром d = 25 мм, на которой установлены вентиль с коэффициентом сопротивления ζв = 3,5, а также диффузор с ζд = 0,5 и диаметром выходного отверстия D = 75 мм. Показание вакуумметра pвак = 10 кПа, высота Н = 2,5 м, h = 2 м. Определить расход Q c учетом всех местных сопротивлений. При решении потерями на трение пренебречь, принять коэффициент сопротивления каждого колена ζкол = 0,5, учесть потери напора на входе в трубу (внезапное сужение) и на выходе в бак (внезапное расширение). Взаимным влиянием сопротивлений пренебречь.
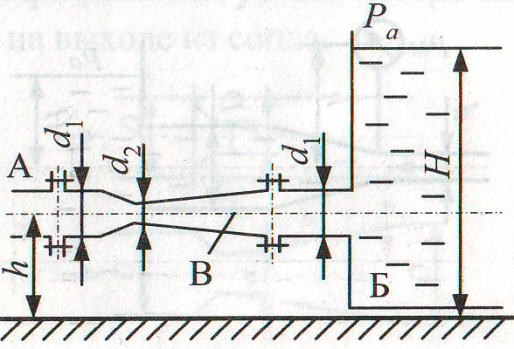 Задача 6.4.Для измерения расхода воды, которая подается по трубе А в бак Б установлен расходомер Вентури В. Определить максимальный расход, который можно пропустить через данный расходомер при условии отсутствия в нем кавитации, если давление насыщенных паров соответствует hн.п. = 2 мм вод.ст. Уровень воды в баке поддерживается постоянным, равным H = 1,5 м, высота расположения трубы h = 0,5 м. Размеры расходомера: d1 = 50 мм и d2 = 20 мм. Атмосферное давление принять соответствующим 760 мм рт.ст., коэффициент сопротивления диффузора ζдиф = 0,2. Учесть потери на внезапное расширение при входе в бак.
Задача 6.4.Для измерения расхода воды, которая подается по трубе А в бак Б установлен расходомер Вентури В. Определить максимальный расход, который можно пропустить через данный расходомер при условии отсутствия в нем кавитации, если давление насыщенных паров соответствует hн.п. = 2 мм вод.ст. Уровень воды в баке поддерживается постоянным, равным H = 1,5 м, высота расположения трубы h = 0,5 м. Размеры расходомера: d1 = 50 мм и d2 = 20 мм. Атмосферное давление принять соответствующим 760 мм рт.ст., коэффициент сопротивления диффузора ζдиф = 0,2. Учесть потери на внезапное расширение при входе в бак.
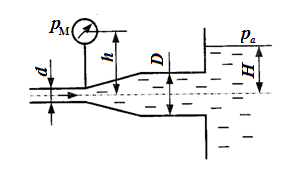 Задача 6.5. Определить расход воды, вытекающей из трубы диаметром d = 22 мм через плавное расширение (диффузор) и далее по трубе диаметром D = 28 мм в бак. Коэффициент сопротивления диффузора ξдиф = 0,2 (отнесен к скорости в трубе диаметром d), показание манометра pм = 20 кПа; высота h = 0,7 м, H = 6 м. Учесть потери на внезапное расширение, потерями на трение пренебречь, режим течения считать турбулентным.
Задача 6.5. Определить расход воды, вытекающей из трубы диаметром d = 22 мм через плавное расширение (диффузор) и далее по трубе диаметром D = 28 мм в бак. Коэффициент сопротивления диффузора ξдиф = 0,2 (отнесен к скорости в трубе диаметром d), показание манометра pм = 20 кПа; высота h = 0,7 м, H = 6 м. Учесть потери на внезапное расширение, потерями на трение пренебречь, режим течения считать турбулентным.
Задача 6.6.Вода по трубе 1 подается в открытый бак. Во избежание переливания воды через край бака устроена вертикальная сливная труба 2 диаметром d = 50 мм. Определить необходимую длину L трубы 2 из условия, чтобы при Q = 10 л/с вода не переливалась через край бака. Режим течения 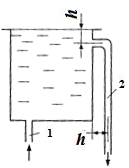 считать турбулентным, а величинами h пренебречь (h = 0). Принять следующие коэффициенты сопротивления: на входе в трубу ζ1 = 0,5, в колене ζ2 = 0,5, на трение по длине трубы λ = 0,03.
считать турбулентным, а величинами h пренебречь (h = 0). Принять следующие коэффициенты сопротивления: на входе в трубу ζ1 = 0,5, в колене ζ2 = 0,5, на трение по длине трубы λ = 0,03.
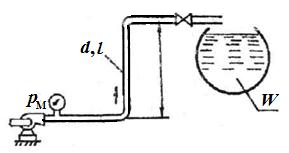 Задача 6.7. По трубопроводу диаметром d = 50 мм насос перекачивает воду на высоту Н = 10 м. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W = 40 м3, если манометр, установленный на выходе из насоса, показывает избыточное давление рм = 250 кПа. Сопротивлением трубопровода пренебречь.
Задача 6.7. По трубопроводу диаметром d = 50 мм насос перекачивает воду на высоту Н = 10 м. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W = 40 м3, если манометр, установленный на выходе из насоса, показывает избыточное давление рм = 250 кПа. Сопротивлением трубопровода пренебречь.
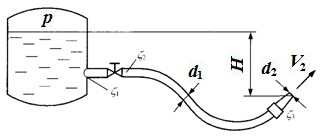
Задача 6.8.Определить давление в напорном баке р, необходимое для получения скорости истечения из брандспойта V2 = 20 м/с. Длина шланга l = 20 м, диаметр d1 = 20 мм, диаметр выходного отверстия брандспойта d2 = 10 мм. Высота уровня воды в баке над отверстием брандспойта Н = 5 м. Учесть местные гидравлические сопротивления при входе в трубу ζ1 = 0,5, в кране ζ2 = 3,5, в брандспойте ζ3 = 0,1, который отнесен к скорости V2, потери на трение в трубе λ = 0,018.
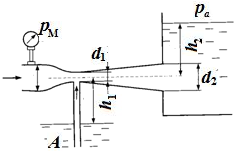
Задача 6.9.Определить минимальное давление pм, измеряемое манометром перед сужением трубы, при котором будет происходить подсасывание воды из резервуара А в узком сечении трубы. Диаметры трубы d1 = 60 мм и d2 = 20 мм высота ее расположения h1 = 6 м, высота уровня жидкости в баке h2 = 1 м. Принять коэффициенты сопротивления сопла ζсоп = 0,08, диффузора ζдиф = 0,3.
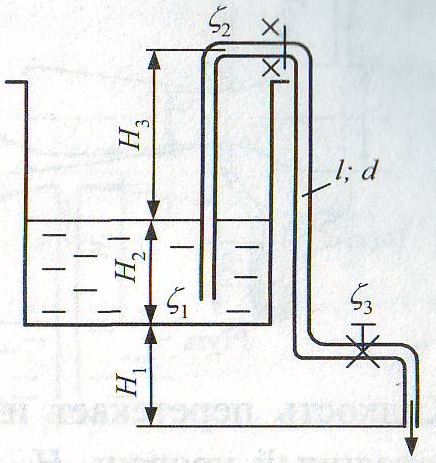 Задача 6.10. Определить расход воды через сифонный трубопровод, если высота H1 = 1 м, Н2 = 2 м, Н3 = 4 м. Общая длина трубы l = 20 м, диаметр d = 20 мм. Режим течения считать турбулентным. Учесть потери на входе в трубу ζ1 = 1, в коленах ζ2 = 0,2, в вентиле ζ3 = 4, на трение в трубе λ = 0,035. Подсчитать вакуум в верхнем сечении х-х трубы, если длина участка от входа в трубу до этого сечения lх = 8 м.
Задача 6.10. Определить расход воды через сифонный трубопровод, если высота H1 = 1 м, Н2 = 2 м, Н3 = 4 м. Общая длина трубы l = 20 м, диаметр d = 20 мм. Режим течения считать турбулентным. Учесть потери на входе в трубу ζ1 = 1, в коленах ζ2 = 0,2, в вентиле ζ3 = 4, на трение в трубе λ = 0,035. Подсчитать вакуум в верхнем сечении х-х трубы, если длина участка от входа в трубу до этого сечения lх = 8 м.
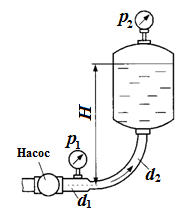
Задача 6.11. Насос нагнетает водув напорный бак, где установились постоянный уровень на высоте H = 3,5 ми постоянное давление р2 = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 80 мм, показывает p1 = 0,3 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d2 = 65 мм; коэффициент сопротивления этой трубы принят равным ζ = 0,2.
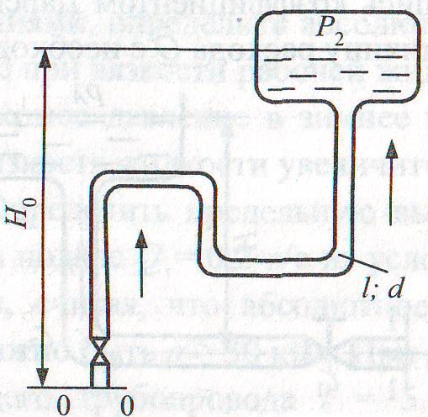 Задача 6.12.Определить потребный напор, который необходимо создать в сечении 0-0 для подачи в бак воды вязкостью ν = 0,008 Ст, если длина трубопровода l = 80 м, его диаметр d = 50 мм, расход жидкости Q = 15 л/с, высота Hо = 30 м, давление в баке р2 = 0,2 МПа, коэффициент сопротивления крана ζ1 = 5, колена ζ2 = 0,8, а шероховатость стенок трубы Δ = 0,04. Потерями на расширение потока пренебречь.
Задача 6.12.Определить потребный напор, который необходимо создать в сечении 0-0 для подачи в бак воды вязкостью ν = 0,008 Ст, если длина трубопровода l = 80 м, его диаметр d = 50 мм, расход жидкости Q = 15 л/с, высота Hо = 30 м, давление в баке р2 = 0,2 МПа, коэффициент сопротивления крана ζ1 = 5, колена ζ2 = 0,8, а шероховатость стенок трубы Δ = 0,04. Потерями на расширение потока пренебречь.
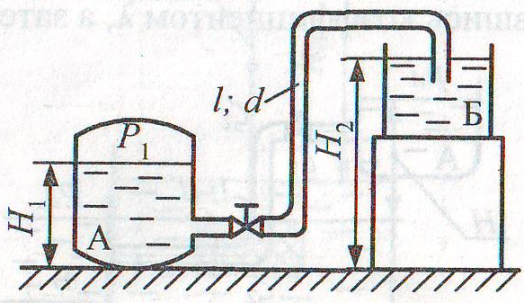
Задача 6.13. Вода перетекает из бака А в резервуар Б по трубе диаметром d = 25 мм, длиной l = 10 м. Определить расход воды Q, если избыточное давление в баке р1 = 200 кПа, высота уровней Н1 = 1 м, Н2 = 5 м. Режим течения считать турбулентным. Принять следующие коэффициенты сопротивления: на входе в трубу ζ1 = 0,5, в вентиле ζ2 = 4, в коленах ζ3 = 0,2, на трение λ = 0,025. Учесть потери при выходе трубопровода в бак Б.
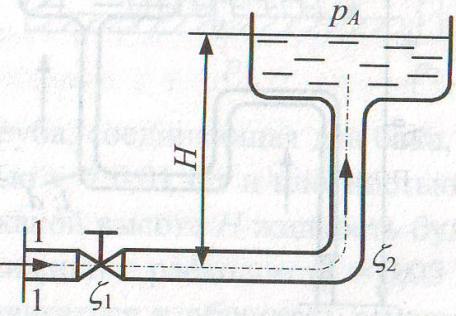 Задача 6.14. Определить расход в трубе для подачи воды с вязкостью ν = 0,01 Ст на высоту H = 16,5 м, если диаметр трубы d = 10 мм, ее длина l = 20 м и располагаемый напор в сечении трубы перед краном Hрасп = 20 м. При решении принять коэффициент сопротивления крана ζ1 = 4, колена ζ2 = 1, а потерями на расширение потока и скоростным напором в трубопроводе пренебречь. Трубу считать гидравлически гладкой.
Задача 6.14. Определить расход в трубе для подачи воды с вязкостью ν = 0,01 Ст на высоту H = 16,5 м, если диаметр трубы d = 10 мм, ее длина l = 20 м и располагаемый напор в сечении трубы перед краном Hрасп = 20 м. При решении принять коэффициент сопротивления крана ζ1 = 4, колена ζ2 = 1, а потерями на расширение потока и скоростным напором в трубопроводе пренебречь. Трубу считать гидравлически гладкой.
Указание: Задачу решить методом последовательных приближений, задавшись коэффициентом Дарси λ, а затем, уточняя его, найти величину расхода Q с необходимой точностью.
Задача 6.15. Определить расход воды с вязкостью ν = 0,01 Ст, перетекающей через трубу из бака А в резервуар Б, если диаметр трубы d = 20 мм, ее длина l = 10 м, высота Н = 8 м. При решении принять коэффициент сопротивления крана ζ1 = 3, каждого колена ζ2 = 1, а эквивалентную шероховатость трубы Δ = 0,05 мм. Учесть 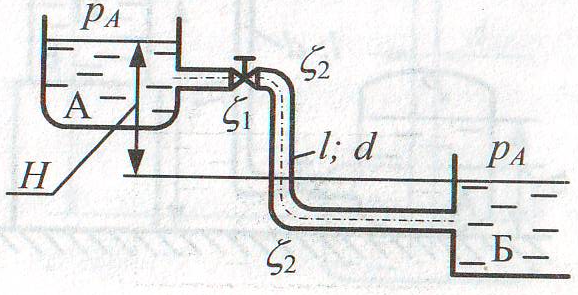 потери на внезапное сужение потока при выходе из бака А и внезапное расширение при входе потока в резервуар Б.
потери на внезапное сужение потока при выходе из бака А и внезапное расширение при входе потока в резервуар Б.
Указание: Задачу решить методом последовательных приближений, задавшись коэффициентом Дарси λ, а затем, уточняя его.
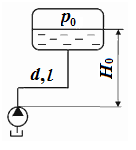 Задача 6.16. Определить предельную высоту всасывания масла насосом при подаче Q = 0,4 л/с из условия бескавитационной работы насоса, считая, что абсолютное давление перед входом в насосе должно быть p ≥ 30 кПа. Длина и диаметр всасывающего трубопровода: l = 2 м; d = 20 мм. Плотность масла ρ = 900 кг/м3, вязкость ν = 2 Ст. Атмосферное давление 750 мм.рт.ст. Сопротивлением входного фильтра пренебречь.
Задача 6.16. Определить предельную высоту всасывания масла насосом при подаче Q = 0,4 л/с из условия бескавитационной работы насоса, считая, что абсолютное давление перед входом в насосе должно быть p ≥ 30 кПа. Длина и диаметр всасывающего трубопровода: l = 2 м; d = 20 мм. Плотность масла ρ = 900 кг/м3, вязкость ν = 2 Ст. Атмосферное давление 750 мм.рт.ст. Сопротивлением входного фильтра пренебречь.
Задача 6.17. При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Hрасп = 9,6 м; длина трубопровода l = 10 м; эквивалентная шероховатость Δ = 0,05 мм; давление в баке p0 = 30 кПа; высота H0 = 4 м; вязкость жидкости ν = 0,015 Ст и ее плотность ρ = 1000 кг/м3? Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.
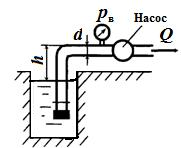 Задача 6.18. Определить максимальный расход воды Q, который можно допустить во всасывающем трубопроводе насоса из условия отсутствия кавитации перед входом в насос, если высота всасывания h = 4 м, размеры трубопровода: l = 6 м; d = 24 мм; предельное давление бензина принять рв = 40 кПа. Режим течения считать турбулентным. Коэффициент сопротивления приемного фильтра ζф = 2; коэффициент сопротивления трения λт = 0,03; h0 = 750 мм.рт.ст.; ρб = 1000 кг/м3.
Задача 6.18. Определить максимальный расход воды Q, который можно допустить во всасывающем трубопроводе насоса из условия отсутствия кавитации перед входом в насос, если высота всасывания h = 4 м, размеры трубопровода: l = 6 м; d = 24 мм; предельное давление бензина принять рв = 40 кПа. Режим течения считать турбулентным. Коэффициент сопротивления приемного фильтра ζф = 2; коэффициент сопротивления трения λт = 0,03; h0 = 750 мм.рт.ст.; ρб = 1000 кг/м3.
Задача 6.19. Определить абсолютное давление жидкости перед входом в центробежный насос при подаче Q = 1 л/с и высоте всасывания h = 0,6 м. Всасывающую трубу, длина которой l = 7,6 м, диаметр d = 20 мм, считать гидравлически гладкой. Учесть сопротивление приемного клапана с фильтрующей сеткой ζф = 3. Вязкость жидкости ν = 0,006 Ст, ее плотность ρ = 750 кг/м3. Скоростным напором при входе в насос пренебречь. Атмосферное давление соответствует 750 мм.рт.ст.
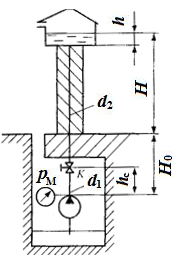 Задача 6.20. Вода с вязкостью ν = 0,02 Ст нагнетается насосом из колодца в водонапорную башню по вертикальному трубопроводу. Определить диаметр трубы от крана К до бака d2, если высота башни Н = 10 м, глубина погружения насоса Но = 5 м, высота уровня жидкости в баке h = 1 м, длина участка трубопровода от насоса до крана ζк = 3, показание манометра рм = 0,3 МПа, а подача насоса Q = 1,5 л/с. При решении пренебречь скоростным напором на выходе из насоса, но учесть потерю скоростного напора при входе в бак. Трубы считать гидравлически гладкими.
Задача 6.20. Вода с вязкостью ν = 0,02 Ст нагнетается насосом из колодца в водонапорную башню по вертикальному трубопроводу. Определить диаметр трубы от крана К до бака d2, если высота башни Н = 10 м, глубина погружения насоса Но = 5 м, высота уровня жидкости в баке h = 1 м, длина участка трубопровода от насоса до крана ζк = 3, показание манометра рм = 0,3 МПа, а подача насоса Q = 1,5 л/с. При решении пренебречь скоростным напором на выходе из насоса, но учесть потерю скоростного напора при входе в бак. Трубы считать гидравлически гладкими.
Указание: Задачу решить методом последовательных приближений, задавшись начальным значением диаметра трубопровода d, а затем, уточняя его, найти величину d с необходимой точностью.
Контрольные вопросы и задания
1. Назовите виды гидравлических сопротивлений, вызывающие потери напора.
2. Что называется коэффициентом гидравлического трения? От чего он зависит?
3. Напишите уравнение Дарси для потерь напора на трение по длине потока и объясните его смысл.
4. Что называется местными сопротивлениями? Дайте определение в общей форме и перечислите наиболее распространенные виды сопротивлений.
5. Как определить потери напора при резком расширении потока?
6. Что называется коэффициентом местных потерь? Как он определяется?
7. Что понимают под эквивалентной длиной местного сопротивления?
8. Какие трубопроводы называют простыми и сложными.
9. Какие задачи ставятся при расчете трубопроводов?
10. В чем заключается расчет простого трубопровода?
11. Что такое высота всасывания? Каковы ее теоретические и практические значения для всасывающих труб?
1. Классификация трубопроводов. Примеры их назначения и использования.
2. Сифоны, их практическое применение.
3. Гидравлический таран, устройство, принцип действия, область применения.
§
Основным вопросом, который интересует при изучении законов истечения жидкости, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Отверстия делят на малые и большие. Отверстие считается малым, если напор превышает 10 наибольших вертикальных размеров отверстия. Отверстием в тонкой стенке считают отверстие, толщина стенки δ которого не превышает диаметр отверстия d.
Скорость струипри истечение через отверстие в тонкой стенке определяется по формуле
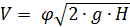 , (7.1)
, (7.1)
где 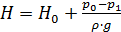 – расчетный напор;
– расчетный напор;
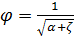 – коэффициент местного сопротивления.
– коэффициент местного сопротивления.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения струи. Вследствие сжатия струи, площадь ее сечения меньше площади отверстия. Степень этого сжатия учитывается с помощью коэффициента сжатия:
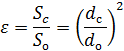
где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.
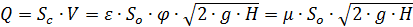 (7.2)
(7.2)
Часто вместо расчетного напора H используют перепад давления
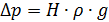 , тогда
, тогда
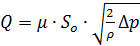 (7.3)
(7.3)
Траекторией оси струи называют ось струи жидкости, свободно падающей после истечения через отверстие. Координаты оси струи х и у связаны между собой соотношениями
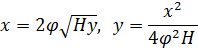
Значения коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ при истечении жидкости через отверстие в тонкой стенке определяются числом Рейнольдса. Для маловязких жидкостей (вода, бензин, керосин), истечение которых происходит при достаточно больших числах Рейнольдса (Re >105), коэффициенты истечения практически не меняются (ε = 0,64, ζ = 0,065, φ = 0,97, α = 1 и μ = 0,62).
При истечении жидкости под уровень скорость и расход определяются по таким же формулам, но коэффициенты истечения несколько меньше, чем при свободном.
Внешний цилиндрический насадок представляет короткую трубку, приставленную к отверстию снаружи, либо отверстие с диаметром в 2 и более раз меньше толщины стенки. Истечение через такой насадок в газовую среду может происходить в двух режимах: безотрывном и отрывном.
При безотрывном режиме струя после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке, затем постепенно расширяется до размеров отверстия из насадка выходит полным сечением.
Коэффициент расхода μ зависит от относительной длины насадка l/d и числа Рейнольдса. Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1, следовательно, μ =φ =0,82, а коэффициент сопротивления ζ = 0,5.
Отрывной режимхарактеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов.
Внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, на втором – очень низкий коэффициент расхода. Он может быть значительно улучшен путем закругления входной кромки или устройства конического входа.
Внутренний цилиндрический насадок представляет короткую трубку, приставленную к отверстию изнутри. В этом случае возможны те же режимы истечения с другими значениями коэффициентов: ζ = 1, μ = 0,71 и μ ≈ ε = 0,5 при первом и втором режимах, соответственно. Коэффициенты истечения из различных насадков представлены в приложении 10.
При истечении жидкости при переменном напоре часто требуется определить время наполнения или опорожнения резервуара.
В случае отсутствия притока жидкости для резервуаров с постоянной площадью свободной поверхности 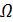 время частичного опорожнения через отверстие
время частичного опорожнения через отверстие
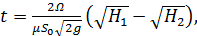 (7.4)
(7.4)
где 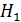 ,
, 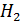 – уровни жидкости в начальный и конечный моменты времени;
– уровни жидкости в начальный и конечный моменты времени; 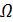 – площадь горизонтального сечения резервуара (площадь поверхности жидкости в резервуаре);
– площадь горизонтального сечения резервуара (площадь поверхности жидкости в резервуаре); 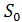 – площадь сечения отверстия.
– площадь сечения отверстия.
Время полного опорожнения определятся по формуле
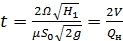 (7.5)
(7.5)
где 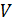 – объем жидкости в резервуаре в начальный момент времени;
– объем жидкости в резервуаре в начальный момент времени; 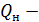 расход жидкости в начальный момент времени.
расход жидкости в начальный момент времени.
§
Пример 7.1.Вода вытекает из закрытого резервуара в атмосферу через отверстие диаметром d = 20 мми коэффициентом расхода μ = 0,62. Глубина погружения центра отверстия h = 0,45 м, избыточное давление на поверхности жидкости p0и = 8,3 кПа. Определить расход жидкости. Как изменится избыточное давление для пропуска того же расхода, если к отверстию присоединить внешний насадок длиной l = 0,1 м.
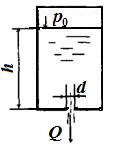 Решение:
Решение:
Расход при истечении жидкости через отверстие определяется по формуле
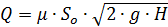
где 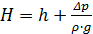 – расчетный напор,
– расчетный напор, 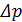 – перепад давления на отверстии (
– перепад давления на отверстии ( 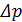 = p0и, т.к. за отверстием давление равно атмосферному);
= p0и, т.к. за отверстием давление равно атмосферному); 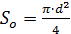 – площадь отверстия.
– площадь отверстия.
Вычислим расход воды через отверстие 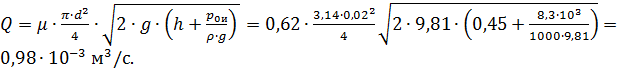
Если к отверстию в дне резервуара присоединить цилиндрический насадок длиной l того же диаметра, то формула примет следующий вид
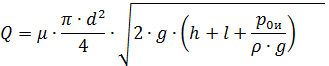
тогда избыточное давление
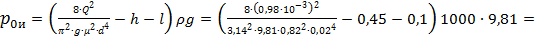 1830 кПа
1830 кПа
Пример 7.2.В пароохладитель через трубку со сверлениями поступает охлаждающая вода температурой 20°С расходом Q = 0,00278 м3/с. Давление воды в трубке p1 = 106 Па, давление в корпусе пароохладителя p2 = 0,7×106 Па. Определить, сколько отверстий диаметром d = 0,003 м нужно просверлить в трубке для обеспечения заданного расхода воды.
Решение:
Плотность воды при температуре 20°С ρ = 998,2 кг/м3 (табл.4.1), кинематический коэффициент вязкости ν = 10-6 м2/с (табл.4.5).
Определим число Рейнольдса, характеризующее истечение из отверстий:
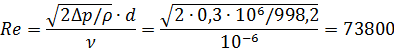
По графику (Приложение 8) определяем коэффициент расхода отверстия μ = 0,6.
Расход воды протекающей через одно отверстие,
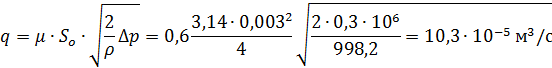
Таким образом, необходимое число отверстий
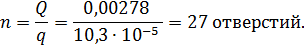
Пример 7.3.Определить время опорожнения цистерны с мазутом при следующих данных: объем мазута в цистерне W = 50 м3; диаметр цистерны D = 2,8 м; диаметр сливного патрубка d = 0,1 м; кинематическая вязкость мазута ν = 0,69·10-4 м2/с.
Решение:Для определения времени опорожнения при известном объеме наполнения резервуара воспользуемся формулой
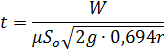
где 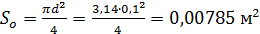 – площадь сливного патрубка; r – радиус цистерны.
– площадь сливного патрубка; r – радиус цистерны.
Коэффициент расхода определим по графику в Приложении 9 в зависимости от числа Рейнольдса. Число Рейнольдса определим по теоретической скорости
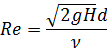
в начале истечения при Н = 2,8 м:
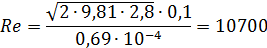
в конце истечения при Н = 0,01 м:

По графику определяем, что соответствующие коэффициенты расхода будут: 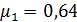 (в начале истечения),
(в начале истечения), 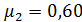 (в конце истечения).
(в конце истечения).
Принимая для расчета среднее значение  и подставляя его в формулу, получим:
и подставляя его в формулу, получим:
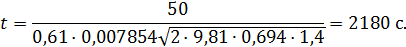
§
Задачи
Методические рекомендации к проведению расчетов
Для решения задач на истечение жидкости через отверстие или насадок при заданном коэффициенте расхода отверстия μ, следует применить формулу (7.2), учитывая при этом, что расчетный напор Н складывается из разности геометрических и пьезометрических высот.
Для определения площади проходного сечения, скорости перемещения поршня, расхода жидкости удобно использовать формулу (7.3). При этом решение сводится к следующим этапам:
1) определить избыточное давление в рабочей полости;
2) найти разность давлений Δр на отверстии;
3) записать уравнение расхода жидкости, вытесняемой поршнем;
4) выразить неизвестную величину.
Если по условию задачи не задан коэффициент расхода, то для его определения необходимо использовать график (Приложение 9). С этой целью нужно
1) определить число Рейнольдса по теоретической скорости (см. пример 7.3);
2) по графику найти точку на графике зависимости μ = f(Re) и определить соответствующее ей значение коэффициента расхода μ.
 Задача 7.1. Определить напор в баке, если расход воды при истечении через цилиндрический насадок диаметром d = 0,05 м составляет Q = 0,05 м3/с. Истечение происходит при постоянном напоре.
Задача 7.1. Определить напор в баке, если расход воды при истечении через цилиндрический насадок диаметром d = 0,05 м составляет Q = 0,05 м3/с. Истечение происходит при постоянном напоре.
Задача 7.2.Определить расход жидкости (ρ = 800 кг/м3), вытекающей из бака через отверстие площадью S0 = 1 см2. Показание ртутного прибора, измеряющего давление воздуха, h = 268 мм, высота H0 = 2 м, коэффициент расхода отверстия µ = 0,60.
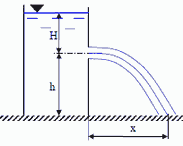 Задача 7.3.Из отверстия диаметром d = 0,4 см в тонкой стенке резервуара вытекает вода, имеющая температуру t = 18 ℃;. Отверстие расположено на высоте h = 8 м над поверхностью земли. Постоянный напор воды в резервуаре H = 6 м. Определить расход и скорость истечения, а также расстояния x, на котором струя коснется поверхности земли.
Задача 7.3.Из отверстия диаметром d = 0,4 см в тонкой стенке резервуара вытекает вода, имеющая температуру t = 18 ℃;. Отверстие расположено на высоте h = 8 м над поверхностью земли. Постоянный напор воды в резервуаре H = 6 м. Определить расход и скорость истечения, а также расстояния x, на котором струя коснется поверхности земли.
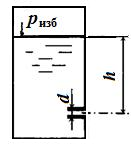 Задача 7.4.Жидкость плотностью ρ = 850 кг/м3 вытекает через установленный на боковой поверхности закрытого резервуара цилиндрический насадок диаметром d = 6 см. Избыточное давление на свободной поверхности жидкости pизб = 6,1 кПа, расход жидкости Q =5 л/с, глубина погружения насадка h = 90 см. Определить коэффициент расхода насадка.
Задача 7.4.Жидкость плотностью ρ = 850 кг/м3 вытекает через установленный на боковой поверхности закрытого резервуара цилиндрический насадок диаметром d = 6 см. Избыточное давление на свободной поверхности жидкости pизб = 6,1 кПа, расход жидкости Q =5 л/с, глубина погружения насадка h = 90 см. Определить коэффициент расхода насадка.
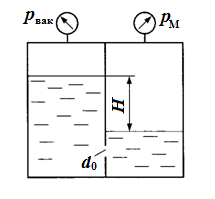
Задача 7.5.Определить направление истечения жидкости (ρ = ρвод) через отверстие d0 = 5 мм и расход, если разность уровней H = 2 м, показание вакуумметра рвак соответствует 147 мм.рт.ст., показание манометра рм = 0,25 МПа, коэффициент расхода μ = 0,62.
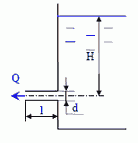 Задача 7.6.Определить расход и скорость воды при истечении из круглого отверстия диаметром d = 0,065 м в тонкой стенке и установить, как они изменяются, если к этому отверстию присоединить цилиндрический насадок длиной l = 4d. Напор в центре тяжести отверстия H = 2,8 м.
Задача 7.6.Определить расход и скорость воды при истечении из круглого отверстия диаметром d = 0,065 м в тонкой стенке и установить, как они изменяются, если к этому отверстию присоединить цилиндрический насадок длиной l = 4d. Напор в центре тяжести отверстия H = 2,8 м.
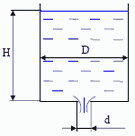 Задача 7.7. Определить объем воды V, налитой в цилиндрический бак диаметром D = 0,8 м, если вся вода вытекла из бака через отверстия в дне диаметром d = 100 мм за время t = 60 c. Какое время t1 потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
Задача 7.7. Определить объем воды V, налитой в цилиндрический бак диаметром D = 0,8 м, если вся вода вытекла из бака через отверстия в дне диаметром d = 100 мм за время t = 60 c. Какое время t1 потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
Задача 7.8. Определить время полного опорожнения открытого резервуара с постоянной площадью сечения Ω объемом V = 50 л через отверстие в дне при начальном расходе Q = 1,8 м3/ч и напоре H = 0,5 м.
Задача 7.9.Время частичного опорожнения вертикально расположенного цилиндрического открытого бака через донное отверстие в тонкой стенке составило t = 40 с. За это время уровень жидкости изменился от h1 = 2 м до h2 = 1 м. Определить диаметр отверстия, если диаметр бака D = 0,5 м.
Задача 7.10.Определить первоначальный уровень в резервуаре h1, если время частичного опорожнения открытого резервуара через донное отверстия до уровня h2 = 0,7 м равно t = 70 с. Диаметр отверстия d = 0,05 м. Размеры поперечного сечения резервуара постоянные a х b = 0,8 х 0,7.
Задача 7.11. Открытый резервуар опоражнивается через коноидальный насадок диаметром d = 5 см. Определить площадь поперечного сечения резервуара, если напор воды за время t = 2 мин понизился на ΔH = 5 см и стал равным H = 35 см. Насадок присоединен к боковой поверхности резервуара.
Задача 7.12. Открытый резервуар с вертикальными стенками опоражнивается через внешний цилиндрический насадок диаметром d = 2,5 см. Через 35 с напор составил H = 1,5 см. Определить расход в начальный момент времени, если площадь поперечного сечения резервуара Ω = 1,75 м2. Насадок 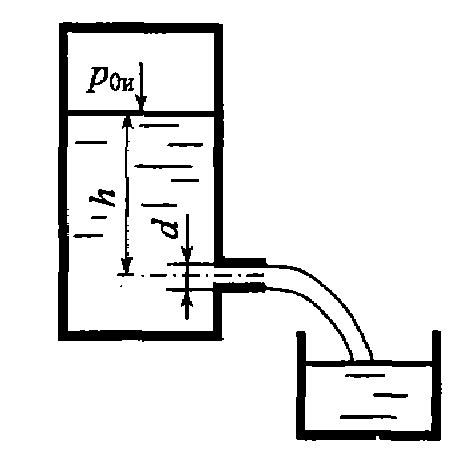 присоединен к отверстию на боковой стенке резервуара.
присоединен к отверстию на боковой стенке резервуара.
Задача 7.13. Определить время наполнения мерного бака объемом V = 0,02 м3, если истечение происходит при постоянном уровне воды, через внешний цилиндрический насадок диаметром d = 0,02 м при избыточном давлении на поверхности воды p0изб = 30 кПа. Глубина погружения насадка h = 2,4 м.
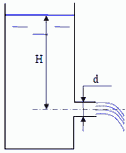
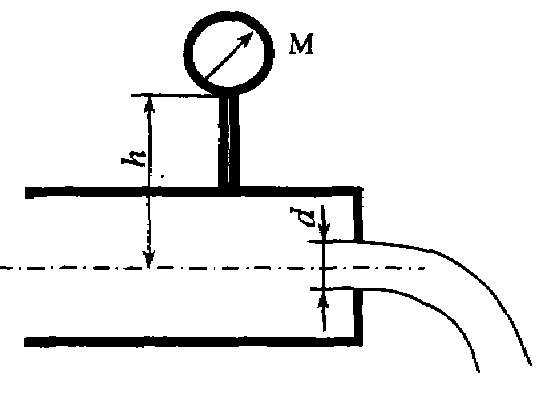
Задача 7.14. Определить расход воды через отверстие диаметром d = 0,08 м, коэффициент расхода которого μ = 0,65, если показание манометра pизб = 150 кПа, а высота установки манометра над осью отверстия h = 1,5 м.
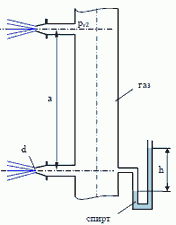 Задача 7.15.Газ, заполняющий вертикальную трубу, вытекает в атмосферу через два насадки диаметром d = 10 мм, расположенные по высоте трубы на расстоянии a = 100 м друг от друга. Коэффициент расхода насадков (с учетом сопротивления подводящих горизонтальных трубок) μ = 0,95.
Задача 7.15.Газ, заполняющий вертикальную трубу, вытекает в атмосферу через два насадки диаметром d = 10 мм, расположенные по высоте трубы на расстоянии a = 100 м друг от друга. Коэффициент расхода насадков (с учетом сопротивления подводящих горизонтальных трубок) μ = 0,95.
Определить массовый расход M газа через каждый насадок, если показание спиртового манометра, присоединенного к трубке у нижнего насадка, h = 200 мм (плотность спирта ρсп = 800 кг/м3).
Давление атмосферного воздуха на уровни нижнего насадка pат = 100 кПа, температура воздуха и газа t = 20 ℃. Значения удельной газовой постоянной воздуха Rв = 287 Дж/(кг·К) и газа Rг = 530 Дж/(кг·К).
Скоростным напором и потерями в трубе пренебречь, плотность воздуха и газа принимать постоянными по высоте a.
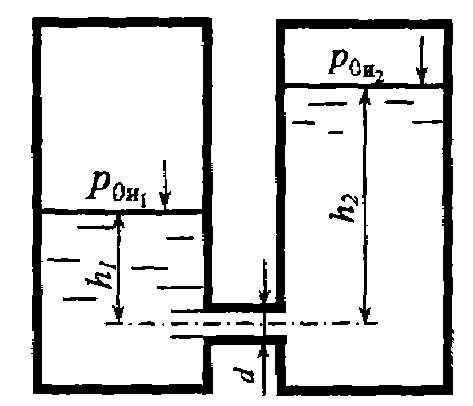 Задача 7.16. Два резервуара с избыточным давлением p0и1 = 105 Па и p0и2 = 0,6·105 Па соединены между собой короткой трубой диаметром d = 20 мм. Определить расход воды в трубе, если h1 = 0,5 м до h2 = 1,4 м.
Задача 7.16. Два резервуара с избыточным давлением p0и1 = 105 Па и p0и2 = 0,6·105 Па соединены между собой короткой трубой диаметром d = 20 мм. Определить расход воды в трубе, если h1 = 0,5 м до h2 = 1,4 м.
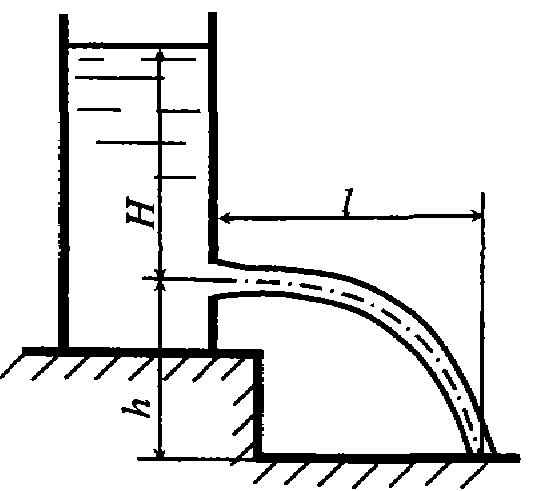 Задача 7.17. Определить коэффициенты расхода, скорости, сжатия при истечении воды в атмосферу через отверстие диаметром d = 10 мм под напором H = 2 м, если расход Q = 0,294 л/с, дальность полета струи l = 3 м. Отверстие расположено на высоте h = 1,2 м от пола.
Задача 7.17. Определить коэффициенты расхода, скорости, сжатия при истечении воды в атмосферу через отверстие диаметром d = 10 мм под напором H = 2 м, если расход Q = 0,294 л/с, дальность полета струи l = 3 м. Отверстие расположено на высоте h = 1,2 м от пола.
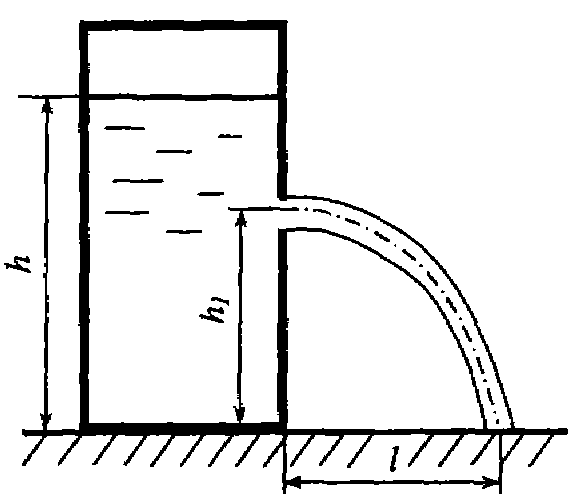 Задача 7.18. Из открытого бака вытекает вода через малое отверстие в атмосферу. Глубина воды в баке h = 3 м поддерживается постоянной. При какой высоте h1 отверстия от пола дальность падения струи l будет максимальной.
Задача 7.18. Из открытого бака вытекает вода через малое отверстие в атмосферу. Глубина воды в баке h = 3 м поддерживается постоянной. При какой высоте h1 отверстия от пола дальность падения струи l будет максимальной.
Задача 7.19. Для задачи 4.18 определить, при какой глубине бака дальность полета будет максимальной, если отверстие расположено на высоте h1 = 1,5 м от основания.
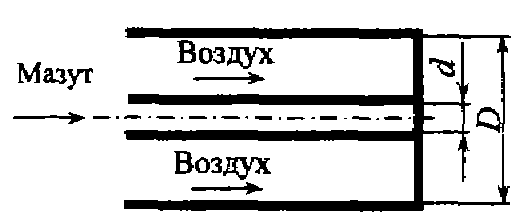
Задача 7.20. Мазут подается в топку котла с расходом Qм = 100 кг/ч. Для сжигания мазута (ρм = 850 кг/м3) требуется воздух (ρв = 850 кг/м3) в количестве V = 8,7 м3/кг. Определить необходимые диаметры каналов для подачи воздуха и мазута, если мазут подается под давлением pи = 2,5 кгс/см2, а воздух под давлением 200 мм рт.ст. Коэффициенты скорости и расхода принять φ = μ = 0,82.
Контрольные вопросы и задания
1. Дайте классификацию отверстий и насадков.
2. Что такое сжатие струи? Какие существуют виды сжатия?
3. Дайте определение коэффициента сжатия, коэффициентов скорости и расхода.
4. Напишите и объясните формулу для определения скорости истечения жидкости из малого отверстия в атмосферу.
5. Чем отличается истечение жидкости из малого отверстия в атмосферу от истечения через затопленное отверстие?
6. В чем различие характера истечения жидкости из малого отверстия и из насадков?
7. Перечислите основные типы насадок и охарактеризуйте особенности истечения из них.
1. Насадки различных типов и их практическое применение.
2. Использование законов истечения жидкости из отверстий и насадков в технике.
3. Динамическое воздействие струи на твердые преграды.
ЛИТЕРАТУРА
Основная литература:
1. Башта Т.М. Гидравлика, гидромашины и гидроприводы/ Т.М. Башта, С.С. Руднев, Б.Б. Некрасов. – М., 1982. – 423 с.
2. Брюханов О.Н., Коробко В.И., Мелик-Аракелян А.Т. Основы гидравлики и гидропривода, – М: «ИНФРА», 2004
3. Некрасов Б.Б., Фатеев И.В., Беленков Ю.А. Задачник по гидравлике, гидромашинам и гидроприводу/ Под ред. Б.Б. Некрасова. – М.: Высшая школа, 1989. – 192 с.
4. Вильнер Я.М., Ковалев Я.Т., Некрасов Б.Б. Справочное пособие по гидравлике, гидромашинам и гидроприводам/ Под ред. Б.Б. Некрасова. Минск, «Вышейшая школа», 1976. – 416 с.
5. Пример расчетов по гидравлике. Под редакцией А.Д. Альтшуля. – М: «Стройздат», 1977
Дополнительная литература:
1. В.Г. Гейер, В.С.Дулин, А.Г. Боруменский, А.Н. Заря. Гидравлика и гидропривод, – М: «Недра», 1970
2. Вихарев А.Н. Решение прикладных задач по гидромеханике: Учебное пособие.-Архангельск, 2000. – 76 с.
3. Г.Я. Суров, А.Н. Вихарев, И.И. Долгова, В.А. Барабанов. Прикладные задачи по гидравлике: Учебное пособие.- Архангельск: АГТУ, 2003. – 236 с.
Приложение 1
§
Значения коэффициента объемного сжатия воды
Плотность воды при различных температурах
Физические свойства воды
В гидравлических расчетах
Множители и приставки для единиц, применяемые
Соотношение между единицами физических величин
Международная система единиц СИ
| Величина | Наименование | Обозначение |
| Длина | метр | м |
| Площадь | квадратный метр | м2 |
| Объем | кубический метр | м3 |
| Скорость | метр в секунду | м/с |
| Ускорение | метр на секунду в квадрате | м/с2 |
| Частота вращения | обороты в секунду | об/с |
| Масса | килограмм | кг |
| Плотность | килограмм на кубический метр | кг/м3 |
| Момент инерции | метр в четвертой степени | м4 |
| Сила (вес) | ньютон | Н |
| Момент силы | ньютон-метр | Н·м |
| Давление, напряжение | паскаль | Па |
| Модуль упругости | паскаль | Па |
| Поверхностное натяжение | ньютон на метр | Н/м |
| Динамический коэффициент вязкости | паскаль-секунда | Па·с |
| Кинематический коэффициент вязкости | квадратный метр на секунду | м2/с |
| Удельный вес | ньютон на кубический метр | Н/м3 |
| Массовый расход | килограмм в секунду | кг/с |
| Объемный расход | кубический метр в секунду | м3/с |
| Мощность | ватт | Вт |
| Температура | кельвин | К |
Приложение 2
| Величина | Наименование | Обозначение | Значение в единицах СИ |
| Сила (вес) | килограмм-сила | кгс | 9,806 Н |
| Давление | килограмм-силы на квадратный сантиметр (техническая атмосфера) | кгс/см2 (ат) | 9,80665·104 Па |
| физическая атмосфера | атм | 1,01325·105 Па | |
| бар | бар | 105 Па | |
| миллиметр ртутного столба | мм рт.ст. | 133,3 Па | |
| миллиметр водного столба | мм вод.ст. | 9,806 Па | |
| Мощность | килограмм-сила-метр в секунду | кгс·м/с | 9,81 Вт |
| лошадиная сила | л.с. | 735,499 Вт | |
| Динамическая вязкость | пуаз | П | 0,1 Па·с |
| Кинематическая вязкость | стокс | Ст | 10-4 м2/с |
| Объем | литр | л | 10-3 м3 |
| Температура | градус Цельсия | °С | Т = (t°C 273) К |
Приложение 3
| Множитель | Приставка | Пример | |
| наименование | обозначение | ||
| 103 | кило | к | килоньютон (кН) |
| 106 | мега | М | мегапаскаль (МПа) |
| 10-1 | деци | д | дециметр (дм) |
| 10-2 | санти | с | сантипуаз (сП) |
| 10-3 | милли | м | миллиметр (мм) |
Приложение 4
Табл. 4.1
| t,°С | Плотность, кг/ м3 | t,°С | Плотность, кг/ м3 | t,°С | Плотность, кг/ м3 |
| 999,67 999,73 | 990,25 988,07 985,73 983,24 980,59 977,81 | 974,89 971,83 968,65 965,34 961,92 959,09 |
Табл. 4.2
| t,°С | 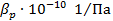 при давлении, Па · при давлении, Па · 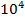 | ||||
| 5,4 5,29 5,23 5,18 5,15 | 5,37 5,23 5,18 5,1 5,05 | 5,31 5,18 5,08 5,03 4,95 | 5,23 5,08 4,98 4,88 4,81 | 5,15 4,93 4,81 4,7 4,6 |
Табл. 4.3
§
Положение центра тяжести плоских фигур
В зависимости от температуры
Значения кинематического коэффициента вязкости воды
В зависимости от давления и температуры
Значения коэффициента температурного расширения воды
От давления и температуры
Значения модуля упругости воды в зависимости
Табл. 4.4
| t,°С | 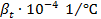 при давлении, · при давлении, · 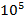 Па Па | ||||
| 1-10 10-20 40-50 60-70 90-100 | 0,14 1,5 4,22 5,56 7,19 | 0,43 1,65 4,22 5,48 7,04 | 0,72 1,83 4,26 5,39 – | 1,49 2,36 4,29 5,23 6,61 | 2,29 2,89 4,37 5,14 6,21 |
Табл. 4.5
| t,°С | ν, 10-4 м2/с при температуре, °С | |
| Чистая вода | Сточная вода | |
| 0,0179 0,0147 0,0138 0,0131 0,0123 0,0117 0,0111 0,0106 0,0101 0,0081 0,0060 0,0056 0,0048 0,0042 0,0037 0,0033 0,0029 | – 0,0167 0,0156-0,0173 0,0147-0,0161 0,0138-0,0152 0,0131-0,0142 0,0123-0,0134 0,0117-0,0127 0,0111-0,012 – – – – – – – – |
Приложение 5
и формулы моментов инерции относительно оси,
проходящей через центр тяжести
Приложение 6
Приложение 7
Значения эквивалентной шероховатости Δ для различных труб
| Вид трубы | Состояние трубы | Δ, мм |
| Тянутая из стекла и цветных металлов | Новая, технически гладкая | 0,001 – 0,01 |
| Бесшовная стальная | Новая и чистая | 0,02 – 0,05 |
| После нескольких лет эксплуатации | 0,15 – 0,30 | |
| Стальная сварная | Новая и чистая | 0,03 – 0,10 |
| С незначительной коррозией после очистки | 0,10 – 0,20 | |
| Умеренно заржавленная | 0,30 – 0,70 | |
| Старая заржавленная | 0,80 – 1,5 | |
| Сильно заржавленная или с большими отложениями | 2,0 – 4,0 | |
| Оцинкованная стальная | Новая | 0,10 – 0,20 |
| После нескольких лет эксплуатации | 0,40 – 0,70 | |
| Чугунная | Новая | 0,20 – 0,50 |
| Бывшая в употреблении | 0,5 – 1,5 | |
| Рукава и шланги резиновые | 0,03 |
Приложение 8
График определения коэффициента гидравлического трения λ = f (Re,d/Δ)








